Atcoder Educational DP Contest
Điểm: 100
Có ~N~ hòn đá, được đánh số từ ~1~ đến ~N~. Với mỗi chỉ số ~i~ ~(1 \le i \le N)~, độ cao của hòn đá thứ ~i~ là ~h_{i}~
Ban đầu, có một chú ếch đang ngồi ở hòn đá thứ nhất và chú sẽ thực hiện liên tục một loạt các hành động sau:
- Nếu chú đang ngồi ở hòn đá ~i~ chú có thể nhảy đến hòn đá thứ ~i+1~ hoặc ~i+2~. Chú sẽ mất chi phí khi nhảy là ~|h_{i} - h_{j}|~ với ~j~ là hòn đá mà chú ếch nhảy đến.
Bạn hãy giúp chú ếch tìm chi phí tối thiểu để nhảy từ hòn đá thứ nhất đến hòn đá thứ ~N~ nhé.
Input
- Dòng đầu tiên của dữ liệu vào chứa số nguyên dương ~N~ ~(2 \le N \le 10^{5})~, là số lượng hòn đá.
- Dòng thứ hai gồm ~N~ số nguyên ~h_{i}~ ~(1 \le i \le N, 1 \le h_{i} \le 10^{4})~, là độ cao của hòn đá thứ ~i~.
Output
- Gồm một số nguyên, là chi phí ít nhất để nhảy từ hòn đá thứ nhất đến hòn đá thứ ~N~.
Sample 1
Input
4
10 30 40 20
Output
30
Giải thích
Một đường đi tối ưu là: ~1 \rightarrow 2 \rightarrow 4~. Chi phí sẽ là ~|10 - 30| + |30 - 20| = 30~.
Sample 2
Input
2
10 10
Output
0
Giải thích
Một đường đi tối ưu là: ~1 \rightarrow 2~. Chi phí sẽ là ~|10 - 10|= 0~.
Sample 3
Input
6
30 10 60 10 60 50
Output
40
Giải thích
Một đường đi tối ưu là: ~1 \rightarrow 3 \rightarrow 5 \rightarrow 6~. Chi phí sẽ là ~|30−60|+|60−60|+|60−50|=40~.
Điểm: 100
Có ~N~ hòn đá, được đánh số từ ~1~ đến ~N~. Với mỗi chỉ số ~i~ ~(1 \le i \le N)~, độ cao của hòn đá thứ ~i~ là ~h_{i}~
Ban đầu, có một chú ếch đang ngồi ở hòn đá thứ nhất và chú sẽ thực hiện liên tục một loạt các hành động sau:
- Nếu chú đang ngồi ở hòn đá ~i~ chú có thể nhảy đến các hòn đá thứ ~i+1~, ~i+2~ ~...~ ~i + K~. Chú sẽ mất phí khi nhảy là ~|h_{i} - h_{j}|~ với ~j~ là hòn đá mà chú ếch nhảy đến.
Bạn hãy giúp chú ếch tìm chi phí tối thiểu để nhảy từ hòn đá thứ nhất đến hòn đá thứ ~N~ nhé.
Input
- Dòng đầu tiên của dữ liệu vào chứa hai số nguyên dương ~N~ và ~K~ ~(2 \le N \le 10^{5}, 1 \le K \le 100)~, lần lượt là số lượng hòn đá và giới hạn nhảy của ếch.
- Dòng thứ hai gồm ~N~ số nguyên ~h_{i}~ ~(1 \le i \le N, 1 \le h_{i} \le 10^{4})~, là độ cao của hòn đá thứ ~i~.
Output
- Gồm một số nguyên, là chi phí ít nhất để nhảy từ hòn đá thứ nhất đến hòn đá thứ ~N~.
Sample 1
Input
5 3
10 30 40 50 20
Output
30
Giải thích
Một đường đi tối ưu là: ~1 \rightarrow 2 \rightarrow 5~. Chi phí sẽ là ~|10 - 30| + |30 - 20| = 30~.
Sample 2
Input
3 1
10 20 10
Output
20
Giải thích
Một đường đi tối ưu là: ~1 \rightarrow 2 \rightarrow 3~. Chi phí sẽ là ~|10 - 20| + |20 - 10| = 20~.
Sample 3
Input
2 100
10 10
Output
0
Giải thích
Một đường đi tối ưu là: ~1 \rightarrow 2~. Chi phí sẽ là ~|10 - 10|= 0~.
Sample 4
Input
10 4
40 10 20 70 80 10 20 70 80 60
Output
40
Giải thích
Một đường đi tối ưu là: ~1 \rightarrow 4 \rightarrow 8 \rightarrow 10~. Chi phí sẽ là ~|40−70|+|70−70|+|70−60|=40~.
Điểm: 100
Kỳ nghỉ hè của Taro bắt đầu vào ngày mai, nên anh ấy đã quyết định lên kế hoạch cho nó ngay bây giờ.
Kỳ nghỉ bao gồm N ngày. Vào ngày thứ ~i~ ~(1 \le i \le N)~, Taro sẽ chọn và tham gia một trong các hoạt động sau:
- A: Bơi ở biển - nhận được ~a_i~ điểm hạnh phúc.
- B: Bắt bọ trên núi - nhận được ~b_i~ điểm hạnh phúc.
- C: Làm bài tập ở nhà - nhận được ~c_i~ điểm hạnh phúc.
Vì Taro dễ cảm thấy buồn chán nên anh không thể tham gia các hoạt động giống nhau trong hai ngày liên tiếp trở lên.
Tìm tổng số điểm hạnh phúc tối đa mà Taro có thể nhận được.
Input
- Dòng đầu tiên là số nguyên ~N~ ~(1 \le N \le 10^5)~
- Dòng thứ ~i~ trong số ~N~ dòng tiếp theo chứa ~3~ số nguyên ~a_i~, ~b_i~, ~c_i~ ~(1 \le a_i, b_i, c_i \le 10^4)~ lần lượt là điểm hạnh phúc có thể nhận được khi Taro tham gia hoạt động ~A, B, C~ của ngày thứ ~i~.
Output
In ra một số nguyên duy nhất là tổng điểm hạnh phúc tối đa mà Taro có thể nhận được.
Sample 1
Input
3
10 40 70
20 50 80
30 60 90
Output
210
Nếu Taro tham gia các hoạt động theo thứ tự ~C, B, C~, anh ấy sẽ có được ~70+50+90=210~ điểm hạnh phúc
Sample 2
Input
1
100 10 1
Output
100
Sample 3
Input
7
6 7 8
8 8 3
2 5 2
7 8 6
4 6 8
2 3 4
7 5 1
Output
46
Taro nên tham gia các hoạt động theo thứ tự : ~C, A, B, A, C, B, A~.
Điểm: 100
Có ~N~ đồ vật được đánh số từ ~1~ đến ~N~. Đồ vật thứ ~i~ ~(1 \le i \le N)~ có khối lượng là ~w_i~ và giá trị là ~v_i~.
Taro quyết định chọn một số đồ vật bỏ vào chiếc túi của anh mang về. Sức chứa tối đa của chiếc túi là ~W~, nghĩa là tổng khối lượng các đồ vật có thể mang tối đa là ~W~.
Hãy tìm tổng giá trị các đồ vật lớn nhất mà Taro có thể mang về nhà.
Input
Dòng đầu tiên chứa hai số nguyên ~N~ ~(1 \le N \le 100)~ và ~W~ ~(1 \le W \le 10^5)~: số lượng đồ vật và sức chứa tối đa của chiếc túi.
~N~ dòng tiếp theo, mỗi dòng chứa hai số nguyên ~w_i~ ~(1 \le w_i \le W)~ và ~v_i~ ~(1 \le v_i \le 10^9)~ lần lượt là khối lượng và giá trị của đồ vật thứ ~i~.
Output
Xuất ra tổng giá trị các đồ vật lớn nhất mà Taro có thể mang về nhà.
Sample 1
Input
3 8
3 30
4 50
5 60
Output
90
Chọn đồ vật ~1~ và ~3~. Tổng khối lượng sẽ là ~3 + 5 = 8~ và tổng giá trị là ~30 + 60 = 90~.
Sample 2
Input
5 5
1 1000000000
1 1000000000
1 1000000000
1 1000000000
1 1000000000
Output
5000000000
Kết quả có thể vượt quá giới hạn kiểu số nguyên ~32~-bit.
Sample 3
Input
6 15
6 5
5 6
6 4
6 6
3 5
7 2
Output
17
Chọn đồ vật ~2~, ~4~ và ~5~. Tổng khối lượng sẽ là ~5 + 6 + 3 = 14~ và tổng giá trị là ~6 + 6 + 5 = 17~.
Điểm: 100
Có ~N~ đồ vật được đánh số từ ~1~ đến ~N~. Đồ vật thứ ~i~ ~(1 \le i \le N)~ có khối lượng là ~w_i~ và giá trị là ~v_i~.
Taro quyết định chọn một số đồ vật bỏ vào chiếc túi của anh mang về. Sức chứa tối đa của chiếc túi là ~W~, nghĩa là tổng khối lượng các đồ vật có thể mang tối đa là ~W~.
Hãy tìm tổng giá trị các đồ vật lớn nhất mà Taro có thể mang về nhà.
Input
Dòng đầu tiên chứa hai số nguyên ~N~ ~(1 \le N \le 100)~ và ~W~ ~(1 \le W \le 10^9)~: số lượng đồ vật và sức chứa tối đa của chiếc túi.
~N~ dòng tiếp theo, mỗi dòng chứa hai số nguyên ~w_i~ ~(1 \le w_i \le W)~ và ~v_i~ ~(1 \le v_i \le 10^3)~ lần lượt là khối lượng và giá trị của đồ vật thứ ~i~.
Output
Xuất ra tổng giá trị các đồ vật lớn nhất mà Taro có thể mang về nhà.
Sample 1
Input
3 8
3 30
4 50
5 60
Output
90
Chọn đồ vật ~1~ và ~3~. Tổng khối lượng sẽ là ~3 + 5 = 8~ và tổng giá trị là ~30 + 60 = 90~.
Sample 2
Input
1 1000000000
1000000000 10
Output
10
Sample 3
Input
6 15
6 5
5 6
6 4
6 6
3 5
7 2
Output
17
Chọn đồ vật ~2, 4~ và ~5~. Tổng khối lượng sẽ là ~5 + 6 + 3 = 14~ và tổng giá trị là ~6 + 6 + 5 = 17~.
Điểm: 100
Bạn được cho hai xâu ~s~ và ~t~. Hãy tìm xâu con chung dài nhất của hai xâu đó.
Lưu ý: Xâu con của xâu ~x~ là xâu được tạo bằng cách xóa ~0~ hoặc một số kí tự thuộc xâu ~x~ và nối các kí tự còn lại mà không thay đổi vị trí của chúng.
Input
Dòng đầu tiên chứa xâu ~s~ ~(1 \le \left| s \right| \le 3000)~.
Dòng thứ hai chứa xâu ~t~ ~(1 \le \left| t \right| \le 3000)~.
Các kí tự của ~s~ và ~t~ đều là các chữ cái Tiếng Anh in thường.
Output
Xuất ra xâu con chung dài nhất của ~s~ và ~t~. Nếu có nhiều xâu thỏa mãn, in ra một xâu bất kì trong các xâu đó.
Sample 1
Input
axyb
abyxb
Output
axb
Kết quả là axb và ayb đều được chấp nhận.
Sample 2
Input
aa
xayaz
Output
aa
Sample 3
Input
a
z
Output
Kết quả có thể là xâu rỗng.
Sample 4
Input
abracadabra
avadakedavra
Output
aaadara
Điểm: 100
Cho đồ thị có hướng ~G~ có ~N~ đỉnh và ~M~ cạnh. Các đỉnh được đánh số từ ~1~ tới ~N~, và cạnh có hướng thứ ~i~ ~(1 \leq i \leq M)~ đi từ đỉnh ~x_i~ tới đỉnh ~y_i~.
Đảm bảo rằng đồ thị ~G~ không có chu trình.
Tìm độ dài đường đi có hướng dài nhất trong đồ thị ~G~, quy ước rằng: độ dài của một đường đi có hướng là số cạnh nằm trên đường đi đó.
Input
Dòng đầu tiên chứa hai số nguyên ~N~ và ~M~, lần lượt là số đỉnh và số cạnh của đồ thị đã cho. ~(2 \leq N \leq 10^5 , 1 \leq M \leq 10^5 ) ~
Dòng thứ ~i~ trong số ~M~ dòng tiếp theo, mỗi dòng chứa hai số nguyên ~x_i~ và ~y_i~, biểu diễn cho cạnh thứ ~i~ của đồ thị.
Đảm bảo rằng tất cả các cạnh ~(x_i, y_i)~ bất kì đều phân biệt và đồ thị ~G~ không có chu trình.
Outout
In ra độ dài của đường đi có hướng dài nhất trong đồ thị ~G~.
Sample 1
Input
4 5
1 2
1 3
3 2
2 4
3 4
Output
3
Giải thích
Đường màu đỏ trong hình dưới đây là đường đi dài nhất:
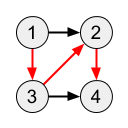
Sample 2
Input
6 3
2 3
4 5
5 6
Output
2
Giải thích
Đường màu đỏ trong hình dưới đây là đường đi dài nhất:
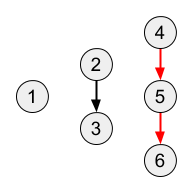
Sample 3
Input
5 8
5 3
2 3
2 4
5 2
5 1
1 4
4 3
1 3
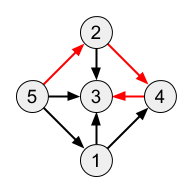
Output
3
Giải thích
Đường màu đỏ trong hình dưới đây là đường đi dài nhất:
Điểm: 100
Cho lưới hình chữ nhật gồm ~H~ hàng và ~W~ cột. Ô ~(i,j)~ được định nghĩa là ô vuông giao giữa hàng thứ ~i~ (từ trên xuống dưới) và cột thứ ~j~ (từ trái qua phải).
Mỗi ô vuông ~(i,j)~ ~(1 \leq i \leq H, 1 \leq j \leq W)~ được biểu diễn bởi 1 kí tự ~a_{i,j}~. Nếu ~a_{i,j}~ là ., ô ~(i,j)~ là một ô rỗng. Ngược lại, nếu ~a_{i,j}~ là #, ô ~(i,j)~ chứa vật cản.
Taro sẽ bắt đầu từ ô ~(1,1)~ đi tới ô ~(H,W)~. Mỗi bước đi, Taro chỉ có thể có di chuyển từ ô hiện tại tới ô liền kề bên phải hoặc ô liền kề phía dưới, với điều kiện ô đó phải là một ô rỗng.
Xác định số đường đi mà Taro có thể đi từ ô ~(1,1)~ tới ô ~(H,W)~. Đáp án có thể rất lớn, vì vậy chỉ in ra phần dư của nó khi chia cho ~10^9 + 7~.
Input
Dòng đầu tiên chứa hai số nguyên ~H~ và ~W~, lần lượt là số hàng và số cột của lưới. ~(2 \leq H, W \leq 1000)~
Dòng thứ ~i~ trong số ~H~ dòng tiếp theo chứa ~W~ kí tự, lần lượt là ~a_{i,1}....a_{i,W}~.
Đảm bảo rằng hai ô ~(1,1)~ và ~(H,W)~ luôn là ô rỗng.
Output
Gồm một số nguyên duy nhất là phần dư của số đường đi thỏa mãn mà Taro có thể đi khi chia cho ~10^9 + 7~.
Sample 1
Input
3 4
...#
.#..
....
Output
3
Giải thích
Có ~3~ cách đi như hình sau:
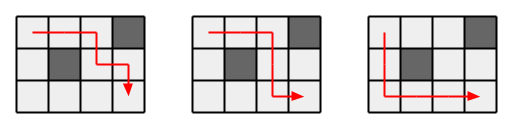
Sample 2
Input
5 2
..
#.
..
.#
..
Output
0
Giải thích
Không có bất cứ cách đi nào thỏa mãn.
Sample 3
Input
5 5
..#..
.....
#...#
.....
..#..
Output
24
Sample 4
Input
20 20
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
Output
345263555
Điểm: 100
Cho ~N~ là một số nguyên dương lẻ.
Có tất cả ~N~ đồng xu được đánh số ~1,2,...,N~. Xác suất để đồng xu thứ ~i~ ~(1 \leq i \leq N)~ lật mặt ngửa khi được tung lên là ~p_{i}~ và xác suất để nó lật mặt sấp khi được tung lên là ~1-p_{i}~.
Taro sẽ tung hết tất cả ~N~ đồng xu. Tìm xác suất để có số mặt ngửa nhiều hơn số mặt sấp.
Input
Dòng đầu tiên chứa số nguyên dương lẻ ~N~ ~(1 \leq N \leq 2999)~
Dòng tiếp theo chứa ~N~ số thực ~p_{i}~ ~(0 < p_{i} < 1)~, mỗi số có hai chữ số thập phân.
Output
In ra xác suất để có số mặt ngửa nhiều hơn số mặt sấp. Kết quả in ra được coi là chính xác nếu sai số tuyệt đối với đáp án không vượt quá ~10^{-9}~.
Sample 1
Input
3
0.30 0.60 0.80
Output
0.612
Giải thích
Xác suất để có số mặt ngửa nhiều hơn số mặt sấp bao gồm các trường hợp:
- Xác suất để có (Ngửa, Ngửa, Ngửa) là ~0.3×0.6×0.8=0.144~;
- Xác suất để có (Sấp, Ngửa, Ngửa) là ~0.7×0.6×0.8=0.336~;
- Xác suất để có (Ngửa, Sấp, Ngửa) là ~0.3×0.4×0.8=0.096~;
- Xác suất để có (Ngửa, Ngửa, Sấp) là ~0.3×0.6×0.2=0.036~.
Do đó, xác suất để có số mặt ngửa nhiều hơn số mặt sấp là ~0.144+0.336+0.096+0.036=0.612~.
Sample 2
Input
1
0.50
Output
0.5
Giải thích:
Kết quả in ra ví dụ như 0.500, 0.500000001 and 0.499999999 đều được coi là chình xác.
Sample 3
Input
5
0.42 0.01 0.42 0.99 0.42
Output
0.3821815872
Điểm: 100
Cho ~N~ cái đĩa được đánh số ~1,2,...,N~. Trước khi bắt đầu, đĩa thứ ~i~ ~(1 \leq i \leq N)~ có ~a_{i}~ ~(1 \leq a_{i} \leq 3)~ miếng sushi.
Taro sẽ thực hiện hành động sau ở mỗi lượt cho tới khi cậu ấy ăn hết tất cả các miếng sushi:
- Đổ một cục xúc xắc ~N~ mặt đánh số ~1,2,…,N~ với cùng xác suất xuất hiện. Gọi ~i~ là số xuất hiện. Nếu có bất kỳ miếng sushi nào trên đĩa thứ ~i~ thì ăn một miếng trong số chúng, nếu đĩa trống thì không làm gì cả.
Tìm giá trị kỳ vọng của số lượt Taro cần thực hiện cho tới khi cậu ấy ăn hết tất cả các miếng sushi.
Input
Dòng đầu tiên chứa số nguyên dương ~N~ ~(1 \leq N \leq 300)~
Dòng tiếp theo chứa ~N~ số nguyên ~a_{i}~ ~(1 \leq a_{i} \leq 3)~
Output
In ra giá trị kỳ vọng của số lượt Taro cần thực hiện cho tới khi cậu ấy ăn hết tất cả các miếng sushi. Kết quả in ra được coi là chính xác nếu sai số tuyệt đối với đáp án không vượt quá ~10^{-9}~.
Sample 1
Input
3
1 1 1
Output
5.5
Giải thích
- Đầu tiên, giá trị kỳ vọng của số lượt Taro cần thực hiện để ăn được miếng sushi thứ nhất là ~1~.
- Sau khi ăn miếng thứ nhất, giá trị kỳ vọng của số lượt Taro cần thực hiện để ăn được miếng sushi thứ hai là ~1.5~.
- Sau khi ăn miếng thứ hai, giá trị kỳ vọng của số lượt Taro cần thực hiện để ăn được miếng sushi thứ ba là ~3~.
Do đó, giá trị kỳ vọng của số lượt Taro cần thực hiện để ăn hết tất cả các miếng sushi là ~1+1.5+3=5.5~.
Sample 2
Input
1
3
Output
3
Giải thích:
Kết quả in ra ví dụ như 3.00, 3.000000003 and 2.999999997 đều được coi là chình xác.
Sample 3
Input
2
1 2
Output
4.5
Sample 4
Input
10
1 3 2 3 3 2 3 2 1 3
Output
54.48064457488221
Điểm: 100
Cho tập hợp gồm ~N~ số nguyên dương ~A=\{a_1,a_2,...,a_N\}~. Taro và Jiro chơi với nhau một trò chơi như sau:
Ban đầu, chúng ta có một đống đá chứa ~K~ viên đá. Hai người chơi sẽ lần lượt thực hiện 1 nước đi như sau, với Taro là người bắt đầu:
- Chọn một phần tử ~x~ của tập ~A~, và loại bỏ đi chính xác ~x~ viên đá từ đống đá.
Người nào không thể thực hiện được nước đi, thì đó là người thua cuộc. Giả sử cả hai người đều chơi tối ưu, xác định người chiến thắng.
Input:
- Dòng thứ nhất chứa hai số nguyên dương ~N, K (1 \leq N \leq 100,1 \leq K \leq 10^5).~
- Dòng thứ hai chứa ~N~ số nguyên dương thỏa mãn ~1\leq a_1 \lt a_2 \lt a_3 \lt ... \lt a_N \leq K.~
Output:
- Nếu Taro là người thắng cuộc, in ra
First, ngược lại nếu Jiro thắng in raSecond.
Sample 1
Input
2 4
2 3
Output
First
Giải thích
Nếu Taro loại 3 viên đá, Jiro không thể thực hiện nước đi. Thế nên, Taro thắng.
Sample 2
Input
2 5
2 3
Output
Second
Giải thích:
Bất kể Taro làm điều gì thì Jiro vẫn thắng vì:
- Nếu Taro loại 2 viên đá, Jiro có thể loại 3 viên đá khiến Taro không thể thực hiện nước đi.
- Nếu Taro loại 3 viên đá, Jiro có thể loại 2 viên đá khiến Taro không thể thực hiện nước đi.
Sample 3
Input
2 7
2 3
Output
First
Giải thích:
Taro nên loại 2 viên đá. Sau đó, bất kể Jiro làm điều gì thì Taro vẫn thắng vì:
- Nếu Jiro loại 2 viên đá, Taro có thể loại 3 viên đá khiến Jiro không thể thực hiện nước đi.
- Nếu Jiro loại 3 viên đá, Taro có thể loại 2 viên đá khiến Jiro không thể thực hiện nước đi.
Sample 4
Input
3 20
1 2 3
Output
Second
Sample 5
Input
3 21
1 2 3
Output
First
Sample 6
Input
1 100000
1
Output
Second
Điểm: 100
Taro và Jiro chơi với nhau một trò chơi như sau:
Cho tập hợp gồm ~N~ số nguyên dương ~a=(a_1,a_2,...,a_N)~. Hai người chơi sẽ lần lượt thực hiện các nước đi sau đến khi ~a~ rỗng, với Taro là người bắt đầu:
- Loại bỏ phần tử đầu tiên hoặc cuối cùng của dãy ~a~. Người chơi đó sẽ kiếm được ~x~ điểm, với ~x~ là phần tử bị loại bỏ.
Cho ~X~ và ~Y~ lần lượt là số điểm của Taro và Jiro sau khi trò chơi kết thúc. Taro muốn ~X - Y~ lớn nhất có thể, trong Jiro lại muốn làm ~X - Y~ bé nhất có thể.
Giả sử cả hai người đều chơi tối ưu, tìm giá trị của ~X - Y~.
Input:
- Dòng thứ nhất chứa hai số nguyên dương ~N (1 \leq N \leq 3000)~.
- Dòng thứ hai chứa ~N~ số nguyên dương thỏa mãn ~a_1, a_2, a_3, ..., a_N (1 \leq a_i \leq 10^9)~.
Output:
- In ra giá trị ~X - Y~ cần tìm.
Sample 1
Input
4
10 80 90 30
Output
10
Giải thích
Trò chơi diễn ra như sau nếu hai người đều chơi tối ưu (với phần tử được in đậm là phần tử được chọn):
- Taro: (10, 80, 90, 30) → (10, 80, 90)
- Jiro: (10, 80, 90) → (10, 80)
- Taro: (10, 80) → (10)
- Jiro: (10) → ()
Ở đây, ~X = 30 + 80 = 110~ và ~Y = 90 + 10 = 100~.
Sample 2
Input
3
10 100 10
Output
-80
Giải thích:
Trò chơi diễn ra như sau nếu hai người đều chơi tối ưu (với phần tử được in đậm là phần tử được chọn):
- Taro: (10, 100, 10) → (100, 10)
- Jiro: (100, 10) → (10)
- Taro: (10) → ()
Ở đây, ~X=10+10=20~ và ~Y=100~.
Sample 3
Input
1
10
Output
10
Sample 4
Input
10
1000000000 1 1000000000 1 1000000000 1 1000000000 1 1000000000 1
Output
4999999995
Sample 5
Input
6
4 2 9 7 1 5
Output
2
Giải thích:
Trò chơi diễn ra như sau nếu hai người đều chơi tối ưu (với phần tử được in đậm là phần tử được chọn):
- Taro: (4, 2, 9, 7, 1, 5) → (4, 2, 9, 7, 1)
- Jiro: (4, 2, 9, 7, 1) → (2, 9, 7, 1)
- Taro: (2, 9, 7, 1) → (2, 9, 7)
- Jiro: (2, 9, 7) → (2, 9)
- Taro: (2, 9) → (2)
- Jiro: (2) → ()
Ở đây, ~X=5+1+9=15~ và ~Y=4+7+2=13~.
Điểm: 100
Có ~N~ đứa trẻ được đánh số từ ~1~ tới ~N~.
Bọn trẻ quyết định chia nhau ~K~ viên kẹo. Với mỗi đứa trẻ, đứa thứ ~i (1 \leq i \leq N)~ phải nhận được số viên kẹo trong phạm vi từ ~0~ tới ~a_i~. ~K~ viên kẹo phải được dùng hết.
Hãy đếm số cách bọn trẻ có thể chia nhau những viên kẹo chia lấy dư cho ~10^9 +7~.
Hai cách chia được gọi là khác nhau nếu tồn tại một đứa trẻ nhận số viên kẹo khác nhau giữa hai cách.
Input
Dòng đầu tiên là hai số nguyên ~N(1 \leq N \leq 100)~ và ~K(0 \leq K \leq 10^5)~.
Dòng thứ hai có ~N~ số nguyên ~a_1,a_2,a_3,...,a_n (0 \leq a_i \leq K).~
Output
Số cách chia kẹo cho bọn trẻ chia lấy dư cho ~10^9 + 7~.
Sample 1
Input
3 4
1 2 3
Output
5
Có ~5~ cách để bọn trẻ chia nhau những viên kẹo như sau:
- ~(0,1,3)~
- ~(0,2,2)~
- ~(1,0,3)~
- ~(1,1,2)~
- ~(1,2,1)~
Ở mỗi dòng số thứ ~i~ là số lượng kẹo mà đứa trẻ thứ ~i~ nhận được.
Sample 2
Input
1 10
9
Output
0
Không có cách chia kẹo thỏa mãn.
Sample 3
Input
2 0
0 0
Output
1
Chỉ có ~1~ cách chia thõa mãn như sau:
- ~(0,0)~
Sample 4
Input
4 100000
100000 100000 100000 100000
Output
665683269
Hãy nhớ chia lấy dư kết quả cho ~10^9 + 7~.
Điểm: 100
Có ~N~ cục thạch xếp thành một hàng ngang. Ban đầu, cục thạch thứ ~i~, đếm từ trái sang, có kích thước ~a_i~.
Taro cố gắng ghép những cục thạch này lại với nhau để tạo thành một cục thạch lớn hơn. Anh ấy sẽ liên tục lặp lại thao tác sau cho đến khi chỉ còn lại một cục thạch duy nhất:
- Taro chọn hai cục thạch kế bên nhau và ghép chúng lại. Cục thạch mới sẽ có kích thước là ~x+y~, ~x~ và ~y~ là kích thước của hai cục thạch được chọn trước khi được ghép. Chi phí phát sinh là ~x+y~ và vị trí tương đối giữa các cục thạch là không thay đổi trong suốt quá trình kết hợp các cục thạch.
Taro là một người tiết kiệm. Bạn hãy giúp Taro tìm chi phí phát sinh nhỏ nhất có thể.
Input
Dòng đầu tiên chứa số nguyên ~N(2 \leq N \leq 400)~ là số lượng cục thạch.
Dòng thứ hai chứ ~N~ số nguyên ~a_1,a_2,a_3,...,a_n (1 \leq a_i \leq 10^9)~.
Output
Dòng duy nhất là chi phí phát sinh nhỏ nhất.
Sample 1
Input
4
10 20 30 40
Output
190
Taro nên thực hiện như sau (những cục thạch được ghép sẽ được in đậm).
- (10, 20, 30, 40) → (30, 30, 40)
- (30, 30, 40) → (60, 40)
- (60, 40) → (100)
Sample 2
Input
5
10 10 10 10 10
Output
120
Taro có thể thực hiện các thao tác như dưới đây:
- (10, 10, 10, 10, 10) → (20, 10, 10, 10)
- (20, 10, 10, 10) → (20, 20, 10)
- (20, 20, 10) → (20, 30)
- (20, 30) → (50)
Sample 3
Input
3
1000000000 1000000000 1000000000
Output
5000000000
Câu trả lời có thể không vừa kiểu int.
Sample 4
Input
6
7 6 8 6 1 1
Output
68
Taro nên thực hiện các thao tác như sau:
- (7, 6, 8, 6,1, 1) → (7, 6, 8, 6, 2)
- (7, 6, 8, 6, 2) → (7, 6, 8, 8)
- (7, 6, 8, 8) → (13, 8, 8)
- (13, 8, 8) → (13, 16)
- (13, 16) → (29)
Điểm: 100
Có ~N~ người đàn ông và ~N~ người phụ nữ đều được đánh số ~1,2,...,N~.
Với mỗi cặp số ~i,j~ ~(1 \le i,j \le N)~, độ hợp nhau của người đàn ông ~i~ và người phụ nữ ~j~ là ~a_{i,j}~. Nếu ~a_{i,j} = 1~ thì ông ~i~ và bà ~j~ hợp nhau, nếu ~a_{i,j} = 0 ~ thì ngược lại.
Taro tìm cách chia ~N~ người đàn ông và ~N~ người phụ nữ thành ~N~ cặp, trong đó mỗi cặp gồm một người đàn ông và một người phụ nữ hợp nhau.
Hãy tìm số cách khác nhau mà Taro có thể chia, modulo ~10^9+7~
Input
Dòng đầu tiên gồm số ~N~ ~(1 \le N \le 21)~.
~N~ dòng sau, mỗi dòng gồm ~N~ số nguyên ~0~ hoặc ~1~. Trong đó số thứ ~j~ ở hàng thứ ~i~ là giá trị của ~a_{i,j}~.
Output
In ra số cách chia cặp thỏa mãn, modulo ~10^9+7~
Sample 1
Input
3
0 1 1
1 0 1
1 1 1
Output
3
Có 3 cách thỏa mãn như sau (~(i,j)~ ký hiệu cho cặp giữa ông ~i~ và bà ~j~)
- ~(1,2),(2,1),(3,3)~
- ~(1,2),(2,3),(3,1)~
- ~(1,3),(2,1),(3,2)~
Sample 2
Input
4
0 1 0 0
0 0 0 1
1 0 0 0
0 0 1 0
Output
1
Có 1 cách thỏa mãn như sau
- ~(1,2),(2,4),(3,1),(4,3)~
Sample 3
Input
1
0
Output
0
Sample 4
Input
21
0 0 0 0 0 0 0 1 1 0 1 1 1 1 0 0 0 1 0 0 1
1 1 1 0 0 1 0 0 0 1 0 0 0 0 1 1 1 0 1 1 0
0 0 1 1 1 1 0 1 1 0 0 1 0 0 1 1 0 0 0 1 1
0 1 1 0 1 1 0 1 0 1 0 0 1 0 0 0 0 0 1 1 0
1 1 0 0 1 0 1 0 0 1 1 1 1 0 0 0 0 0 0 0 0
0 1 1 0 1 1 1 0 1 1 1 0 0 0 1 1 1 1 0 0 1
0 1 0 0 0 1 0 1 0 0 0 1 1 1 0 0 1 1 0 1 0
0 0 0 0 1 1 0 0 1 1 0 0 0 0 0 1 1 1 1 1 1
0 0 1 0 0 1 0 0 1 0 1 1 0 0 1 0 1 0 1 1 1
0 0 0 0 1 1 0 0 1 1 1 0 0 0 0 1 1 0 0 0 1
0 1 1 0 1 1 0 0 1 1 0 0 0 1 1 1 1 0 1 1 0
0 0 1 0 0 1 1 1 1 0 1 1 0 1 1 1 0 0 0 0 1
0 1 1 0 0 1 1 1 1 0 0 0 1 0 1 1 0 1 0 1 1
1 1 1 1 1 0 0 0 0 1 0 0 1 1 0 1 1 1 0 0 1
0 0 0 1 1 0 1 1 1 1 0 0 0 0 0 0 1 1 1 1 1
1 0 1 1 0 1 0 1 0 0 1 0 0 1 1 0 1 0 1 1 0
0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 1 1 0 0 1
0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 0 0 1 1 0 1
0 0 0 0 1 1 1 0 1 0 1 1 1 0 1 1 0 0 1 1 0
1 1 0 1 1 0 0 1 1 0 1 1 0 1 1 1 1 1 0 1 0
1 0 0 1 1 0 1 1 1 1 1 0 1 0 1 1 0 0 0 0 0
Output
102515160
Lưu ý kết quả cần phải được in ra theo modulo ~10^9+7~.
Điểm: 100
Cho 1 cây có ~N~ đỉnh, được đánh số ~1,2,...,N~. Cây có ~N-1~ cạnh, trong đó cạnh thứ ~i~ nối giữa đỉnh ~x_i~ và ~y_i~.
Taro sẽ tô màu mỗi đỉnh trên cây bằng ~1~ trong ~2~ màu đen hoặc trắng. Ngoài ra, không được phép tồn tại ~2~ đỉnh kề mà cả ~2~ đỉnh đều có màu đen.
Tìm số cách tô các đỉnh thỏa mãn, modulo ~10^9+7~
Input
Dòng đầu tiên gồm số nguyên ~N~ ~(1 \le N \le 10^5)~.
~N-1~ dòng tiếp theo, mỗi dòng gồm ~2~ số nguyên. Trong đó dòng thứ ~i~ chứa ~2~ số nguyên ~x_i~ và ~y_i~.
Input đảm bảo đồ thị đã cho là cây.
Output
In ra số cách tô thỏa mãn modulo ~10^9+7~
Sample 1
Input
3
1 2
2 3
Output
5
Có ~5~ cách tô các đỉnh như sau:

Sample 2
Input
4
1 2
1 3
1 4
Output
9
Có ~9~ cách tô các đỉnh như sau:
Sample 3
Input
1
Output
2
Sample 4
Input
10
8 5
10 8
6 5
1 5
4 8
2 10
3 6
9 2
1 7
Output
157
Điểm: 100
Có ~N~ bông hoa được xếp thành một hàng trong vườn hoa của Taro. Với mỗi ~i\,(1 \le i \le N)~, chiều cao và vẻ đẹp của bông hoa thứ ~i~ từ trái sang phải lần lượt là ~h_i~ và ~a_i~. Trong vườn hoa, chiều cao của các bông hoa ~h_1, h_2, \ldots, h_N~ phân biệt đôi một với nhau.
Taro đang nhổ một số bông hoa đi để những bông hoa còn lại trong vườn thỏa mãn điều kiện sau đây:
- Chiều cao của các bông hoa còn lại tăng dần từ trái sang phải.
Taro muốn vườn hoa của mình là đẹp nhất có thể (dĩ nhiên, ai mà chẳng muốn như vậy), vậy nên Taro muốn bỏ đi các bông hoa sao cho tổng vẻ đẹp của những bông hoa còn lại là lớn nhất. Tuy nhiên, Taro đang bận làm bài tập nên đã nhờ bạn làm giúp việc này. Hãy giúp Taro và in ra tổng vẻ đẹp lớn nhất có thể của các bông hoa còn lại.
Input
Dòng thứ nhất chứa một số nguyên ~N\,(1 \le N \le 2 \times 10^5)~.
Dòng thứ hai chứa ~N~ số nguyên ~h_i\,(1 \le h_i \le N)~ phân biệt đôi một.
Dòng thứ ba chứa ~N~ số nguyên ~a_i\,(1 \le a_i \le 10^9)~.
Output
In ra tổng vẻ đẹp lớn nhất có thể của những bông hoa còn lại.
Sample 1
Input
4
3 1 4 2
10 20 30 40
Output
60
Giải thích
Tổng vẻ đẹp lớn nhất của vườn hoa có thể là ~60~, bằng cách giữ lại các bông hoa thứ hai và thứ tư từ trái qua phải.
Sample 2
Input
1
1
10
Output
10
Giải thích
Vườn hoa đã thỏa mãn điều kiện đề bài từ ban đầu.
Sample 3
Input
5
1 2 3 4 5
1000000000 1000000000 1000000000 1000000000 1000000000
Output
5000000000
Sample 4
Input
9
4 2 5 8 3 6 1 7 9
6 8 8 4 6 3 5 7 5
Output
31
Giải thích
Tổng vẻ đẹp lớn nhất của vườn hoa có thể là ~31~, bằng cách giữ lại các bông hoa thứ hai, thứ ba, thứ sáu, thứ tám và thứ chín từ trái qua phải.
Lưu ý
Đáp án có thể vượt quá giới hạn của kiểu biến số nguyên 32-bit.
Điểm: 100
Cho đồ thị có hướng ~G~ có ~N~ đỉnh, được đánh số từ ~1~ tới ~N~, dưới dạng ma trận kề ~a~ là một bảng gồm ~N~ hàng và ~N~ cột.
Với mỗi cặp số ~i~ và ~j~ ~(1 \le i,j \le N)~, số nguyên ~a_{i,j}~ thể hiện rằng có tồn tại hay không một cạnh có hướng từ đỉnh ~i~ tới đỉnh ~j~. Nếu ~a_{i,j} = 1~, thì tồn tại một cạnh có hướng từ đỉnh ~i~ tới đỉnh ~j~; còn nếu ~a_{i,j} = 0~ thì không tồn tại cạnh đó.
Hãy đếm số lượng đường đi khác nhau có độ dài ~K~ trong đồ thị ~G~, chia lấy số dư cho ~10^9 + 7~. Những con đường đi qua một cạnh nhiều lần cũng sẽ được tính.
Input
Dòng đầu tiên chứa hai số nguyên ~N\,(1 \le N \le 50)~ và ~K\,(1 \le K \le 10^{18})~.
~N~ dòng tiếp theo, mỗi dòng chứa ~N~ số nguyên ~a_{i,j}\,(a_{i,j} \in \left \{ 0, 1 \right \}~, ~a_{i, i} = 0)~.
Output
In ra số lượng đường đi khác nhau có độ dài ~K~ trong đồ thị ~G~.
Sample 1
Input
4 2
0 1 0 0
0 0 1 1
0 0 0 1
1 0 0 0
Output
6
Giải thích
Đồ thị ~G~ trông như sau:
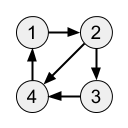
Có sáu đường đi có độ dài ~2~ là:
- ~1 \rightarrow 2 \rightarrow 3~
- ~1 \rightarrow 2 \rightarrow 4~
- ~2 \rightarrow 3 \rightarrow 4~
- ~2 \rightarrow 4 \rightarrow 1~
- ~3 \rightarrow 4 \rightarrow 1~
- ~4 \rightarrow 1 \rightarrow 2~
Sample 2
Input
3 3
0 1 0
1 0 1
0 0 0
Output
3
Giải thích
Đồ thị ~G~ trông như sau:
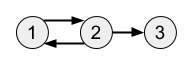
Có ba đường đi có độ dài ~3~ là:
- ~1 \rightarrow 2 \rightarrow 1 \rightarrow 2~
- ~2 \rightarrow 1 \rightarrow 2 \rightarrow 1~
- ~2 \rightarrow 1 \rightarrow 2 \rightarrow 3~
Sample 3
Input
6 2
0 0 0 0 0 0
0 0 1 0 0 0
0 0 0 0 0 0
0 0 0 0 1 0
0 0 0 0 0 1
0 0 0 0 0 0
Output
1
Giải thích
Đồ thị ~G~ trông như sau:
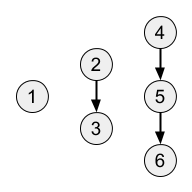
Có đúng một đường đi có độ dài ~2~ là:
- ~4 \rightarrow 5 \rightarrow 6~
Sample 4
Input
1 1
0
Output
0
Sample 5
Input
10 1000000000000000000
0 0 1 1 0 0 0 1 1 0
0 0 0 0 0 1 1 1 0 0
0 1 0 0 0 1 0 1 0 1
1 1 1 0 1 1 0 1 1 0
0 1 1 1 0 1 0 1 1 1
0 0 0 1 0 0 1 0 1 0
0 0 0 1 1 0 0 1 0 1
1 0 0 0 1 0 1 0 0 0
0 0 0 0 0 1 0 0 0 0
1 0 1 1 1 0 1 1 1 0
Output
957538352
Điểm: 100
Hãy đếm số lượng số nguyên (modulo ~10^9+7~) trong phạm vi từ ~1~ đến ~K~ (tính cả ~1~ và ~K~) thoả mãn:
- Tổng các chữ số trong biểu diễn thập phân của số đó là bội của ~D~.
Input
Dòng thứ nhất chứa số nguyên ~K~ ~(1 \le K < 10^{10000})~.
Dòng thứ hai chứa số nguyên ~D~ ~(1 \le D \le 100)~.
Output
In ra số lượng số nguyên thoả mãn điều kiện, modulo ~10^9+7~.
Sample 1
Input
30
4
Output
6
Có ~6~ số nguyên thoả mãn điều kiện là: ~4,8,13,17,22~ và ~26~.
Sample 2
Input
1000000009
1
Hãy nhớ in ra đáp án chia lấy dư cho ~10^9+7~.
Output
2
Sample 3
Input
98765432109876543210
58
Output
635270834
Điểm: 100
Cho xâu ~S~ có độ dài ~N - 1~ gồm 2 kí tự < và >. Tìm số hoán vị (modulo ~10^9 + 7~) ~P_1, P_2, \dots, P_N~ của ~N~ số nguyên dương đầu tiên thoả mãn với mỗi ~1 \leq i < N~:
- ~P_i < P_{i + 1}~ nếu kí tự thứ ~i~ trong xâu ~S~ là
<. - ~P_i > P_{i + 1}~ nếu kí tự thứ ~i~ trong xâu ~S~ là
>.
Input
- Dòng đầu tiên chứa số nguyên dương ~N~ (~2 \leq N \leq 3000~).
- Dòng thứ hai chứa xâu ~S~ độ dài ~N - 1~ chỉ gồm 2 kí tự
<và>.
Output
In ra số hoán vị thoả mãn điều kiện theo modulo ~10^9 + 7~.
Sample test
Sample Input 1
4
<><
Sample Output 1
5
Giải thích
Có ~5~ hoán vị thoả yêu cầu:
- ~(1,3,2,4)~
- ~(1,4,2,3)~
- ~(2,3,1,4)~
- ~(2,4,1,3)~
- ~(3,4,1,2)~
Sample Input 2
5
<<<<
Sample Output 2
1
Giải thích
Có duy nhất ~1~ hoán vị thoả yêu cầu:
- ~(1,2,3,4,5)~
Sample Input 3
20
>>>><>>><>><>>><<>>
Sample Output 3
217136290
Giải thích
Lưu ý kết quả modulo ~10^9 + 7~
Điểm: 100
Có ~N~ chú thỏ được đánh số ~1, 2, 3,..., N~.
Sự hoà đồng giữa hai chú thỏ ~i~ và ~j~ ~(1 \le i, j \le N)~ được biểu diễn bởi số nguyên ~a_{i,j}~. Trong đó, ~a_{i, i} = 0~ ~(1 \le i \le N)~, và ~a_{i, j} = a_{j, i}~ ~(1 \le i, j \le N)~.
Taro đang tìm cách chia ~N~ chú thỏ này vào một số nhóm, sao cho mỗi chú thỏ thuộc chính xác một nhóm. Nếu hai chú thỏ ~i~ và ~j~ ~(1 \le i < j \le N)~ thuộc cùng một nhóm, Taro được ~a_{i, j}~ điểm.
Bạn hãy tìm tổng số điểm lớn nhất mà Taro có thể đạt được.
Input
Dòng đầu tiên chứa số nguyên ~N~ ~(1 \le N \le 16)~.
~N~ dòng tiếp theo, mỗi dòng chứa ~N~ số nguyên, số thứ ~j~ của dòng thứ ~i~ là số nguyên ~a_{i, j}~ ~(|a_{i, j}| \le 10^9, a_{i, i} = 0, a_{i, j} = a_{j, i})~.
Output
In ra tổng số điểm lớn nhất mà Taro có thể đạt được.
Sample 1
Input
3
0 10 20
10 0 -100
20 -100 0
Output
20
Sample 2
Input
2
0 -10
-10 0
Output
0
Sample 3
Input
4
0 1000000000 1000000000 1000000000
1000000000 0 1000000000 1000000000
1000000000 1000000000 0 -1
1000000000 1000000000 -1 0
Output
4999999999
Sample 4
Input
16
0 5 -4 -5 -8 -4 7 2 -4 0 7 0 2 -3 7 7
5 0 8 -9 3 5 2 -7 2 -7 0 -1 -4 1 -1 9
-4 8 0 -9 8 9 3 1 4 9 6 6 -6 1 8 9
-5 -9 -9 0 -7 6 4 -1 9 -3 -5 0 1 2 -4 1
-8 3 8 -7 0 -5 -9 9 1 -9 -6 -3 -8 3 4 3
-4 5 9 6 -5 0 -6 1 -2 2 0 -5 -2 3 1 2
7 2 3 4 -9 -6 0 -2 -2 -9 -3 9 -2 9 2 -5
2 -7 1 -1 9 1 -2 0 -6 0 -6 6 4 -1 -7 8
-4 2 4 9 1 -2 -2 -6 0 8 -6 -2 -4 8 7 7
0 -7 9 -3 -9 2 -9 0 8 0 0 1 -3 3 -6 -6
7 0 6 -5 -6 0 -3 -6 -6 0 0 5 7 -1 -5 3
0 -1 6 0 -3 -5 9 6 -2 1 5 0 -2 7 -8 0
2 -4 -6 1 -8 -2 -2 4 -4 -3 7 -2 0 -9 7 1
-3 1 1 2 3 3 9 -1 8 3 -1 7 -9 0 -6 -8
7 -1 8 -4 4 1 2 -7 7 -6 -5 -8 7 -6 0 -9
7 9 9 1 3 2 -5 8 7 -6 3 0 1 -8 -9 0
Output
132
Note
Các cách chia ở từng test ví dụ:
- Ví dụ ~1~: ~\{1, 3\},\{2\}~.
- Ví dụ ~2~: ~\{1\},\{2\}~.
- Ví dụ ~3~: ~\{1,2,3,4\}~.
Lưu ý rằng đáp án có thể vượt quá phạm vi giá trị của kiểu số nguyên 32-bit.
Điểm: 100
Cây là đồ thị vô hướng, liên thông và không có chu trình. Một cây ~N~ đỉnh sẽ có ~(N - 1)~ cạnh. Cho một cây có ~N~ đỉnh, các đỉnh được đánh số ~1, 2, ..., N~. Cạnh thứ ~i~ ~(1 \le i \le (N - 1))~ kết nối 2 đỉnh ~x_{i}~ và ~y_{i}~.
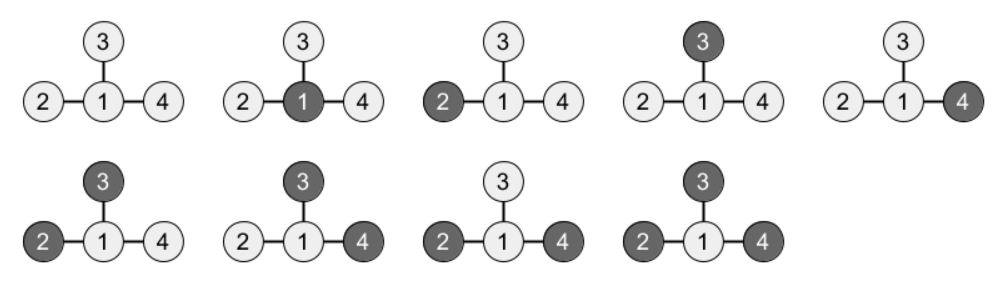
Taro quyết định tô mỗi đỉnh của cây bởi một trong hai màu trắng hoặc đen, sao cho với hai đỉnh được tô đen bất kì, tất cả các đỉnh trên đường đi giữa hai đỉnh đó cũng được tô đen.
Bạn được cho một số nguyên dương ~M~. Với mỗi ~v~ ~(1 \le v \le N)~, hãy trả lời câu hỏi dưới đây:
Giả sử đỉnh ~v~ đã được tô màu đen, có bao nhiêu cách tô ~(n - 1)~ đỉnh còn lại để thỏa mãn điều kiện trên? Do đáp án có thể rất lớn, in ra kết quả modulo ~M~.
Input
Dòng đầu tiên chứa 2 số ~N~ và ~M~ - số đỉnh và modulo.
Dòng thứ ~i~ trong ~(N - 1)~ dòng tiếp theo chứa ~2~ số ~x_{i}~ và ~y_{i}~ - ~2~ đỉnh được nối bởi cạnh thứ ~i~.
Output
In ra ~N~ dòng, dòng thứ ~i~ in ra đáp án cho câu hỏi trên với đỉnh ~i~ theo modulo ~M~.
Giới hạn
- Tất cả các giá trị trong input là số nguyên.
- ~1 \le N \le 10^5~
- ~2 \le M \le 10^9~ (lưu ý rằng ~M~ không nhất thiết phải là số nguyên tố)
- ~1 \le x_{i}, y_{i} \le N~ ~(1 \le i \le (N - 1))~
- Đồ thị đã cho là cây.
Sample Input 1
3 100
1 2
2 3
Sample Output 1
3
4
3
Sample Input 2
4 100
1 2
1 3
1 4
Sample Output 2
8
5
5
5
Sample Input 3
1 100
Sample Output 3
1
Sample Input 4
10 2
8 5
10 8
6 5
1 5
4 8
2 10
3 6
9 2
1 7
Sample Output 4
0
0
1
1
1
0
1
0
1
1
Giải thích test đề thứ nhất
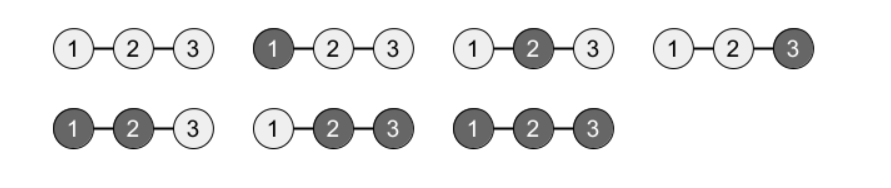
Trên đây là tất cả những cách tô màu thỏa mãn điều kiện đề bài. (Cách tô đỉnh ~1~ và ~3~ đen không thỏa mãn do đồ thị tạo bởi ~2~ đỉnh ~1~ và ~3~ không liên thông)
Trong ~7~ cách trên, có
- ~3~ cách có đỉnh ~1~ được tô màu đen
- ~4~ cách có đỉnh ~2~ được tô màu đen
- ~3~ cách có đỉnh ~3~ được tô màu đen
Điểm: 100
Xét một xâu có chiều dài ~N~ bao gồm các chữ số 0 và 1. Điểm của xâu được tính như sau:
- Với mỗi số nguyên ~i~ (~1~ ≤ ~i~ ≤ ~M~), tổng số điểm của xâu được tăng thêm ~a_i~ nếu như xâu con bao gồm các kí tự từ ~l_i~ đến ~r_i~ (kể cả biên) có ít nhất một kí tự
1.
Với mọi xâu độ dài ~N~, số điểm cao nhất có thể đạt được là bao nhiêu?
Input
- Dòng đầu chứa hai số nguyên ~N, M~ (~1 \le N \le 2 \cdot 10^5~ và ~1 \le M \le 2 \cdot 10^5~).
- ~M~ dòng tiếp theo, mỗi dòng chứa ba số nguyên ~l_i, r_i, a_i~ (~1 \le l_i \le r_i \le N~ và ~\mid a_i\mid \le 10^9~).
Output
Số điểm tối đa mà xâu có thể đạt được.
Sample 1
Input
5 3
1 3 10
2 4 -10
3 5 10
Output
20
Giải thích
Điểm cho xâu 10001 là ~a_1 + a_3 = 10 + 10 = 20~.
Sample 2
Input
3 4
1 3 100
1 1 -10
2 2 -20
3 3 -30
Output
90
Giải thích
Điểm cho xâu 100 là ~a_1 + a_2 = 100 + (-10) = 90~.
Sample 3
Input
1 1
1 1 -10
Output
0
Giải thích
Điểm cho xâu 0 là ~0~.
Sample 4
Input
1 5
1 1 1000000000
1 1 1000000000
1 1 1000000000
1 1 1000000000
1 1 1000000000
Output
5000000000
Kết quả có thể không phù hợp với số nguyên có định dạng 32-bit.
Sample 5
Input
6 8
5 5 3
1 1 10
1 6 -8
3 6 5
3 4 9
5 5 -2
1 3 -6
4 6 -7
Output
10
Giải thích
Điểm cho xâu 101000 là ~a_2 + a_3 + a_4 + a_5 + a_7 = 10 + (-8) + 5 + 9 + (-6) = 10~.
Điểm: 100
Cho ~N~ khối khác nhau được đánh số từ ~1~ tới ~N~. Khối thứ ~i~ (~1 \le i \le N~) có cân nặng ~w_i~, có sức chịu nặng ~s_i~, và có giá trị ~v_i~.
Taro quyết định xây một toà tháp bằng một số khối lấy từ ~N~ khối đã cho và xếp chồng chúng lên nhau theo một thứ tự nhất định. Toà tháp phải thoả mãn điều kiện sau:
- Tổng khối lượng các khối được đặt trên khối thứ ~i~ không được phép lớn hơn ~s_i~.
Tìm tổng giá trị tối đa mà toà tháp có thể đạt được.
Input
- Dòng đầu tiên chứa số nguyên ~N~.
- ~N~ dòng tiếp theo, dòng thứ ~i~ chứa 3 số nguyên ~w_i, s_i, v_i~ lần lượt là cân nặng, sức chịu nặng và giá trị của khối thứ ~i~.
Output
Tổng giá trị tối đa mà toà tháp có thể đạt được.
Giới hạn:
- Mọi giá trị từ input đều là số nguyên.
- ~1 \le N \le 10^3~
- ~1 \le w_i, s_i \le 10^4~
- ~1 \le v_i \le 10^9~
Sample 1
Input
3
2 2 20
2 1 30
3 1 40
Output
50
Giải thích
Nếu như khối ~2~ xếp chồng lên khối ~1~, ta được tổng giá trị tối đa của toà tháp là ~30 + 20 = 50~.
Sample 2
Input
4
1 2 10
3 1 10
2 4 10
1 6 10
Output
40
Giải thích
Các khối ~1, 2, 3, 4~ được xếp theo thứ tự từ đỉnh tới đáy.
Sample 3
Input
5
1 10000 1000000000
1 10000 1000000000
1 10000 1000000000
1 10000 1000000000
1 10000 1000000000
Output
5000000000
Kết quả có thể không phù hợp với số nguyên có định dạng 32-bit.
Sample 4
Input
8
9 5 7
6 2 7
5 7 3
7 8 8
1 9 6
3 3 3
4 1 7
4 5 5
Output
22
Giải thích
Chúng ta có thể xếp các khối ~5, 6, 8, 4~ theo thứ tự từ đỉnh tới đáy.
Điểm: 100
Có một lưới ô vuông gồm ~H~ hàng và ~W~ cột. Toạ độ ~(i, j)~ biểu thị cho ô vuông ở hàng ~i~ từ trên xuống và cột ~j~ từ trái sang. Trong lưới ô vuông có ~N~ ô ~(r_1,c_1), (r_2,c_2), ...(r_n,c_n)~ là những ô có chướng ngại vật, ngoài những ô này ra tất cả các ô còn lại là các ô trống có thể đi được. Lưới ô vuông đảm bảo rằng ô ~(1,1)~ và ô ~(H, W)~ là ô trống.
Taro sẽ bắt đầu ở ô ~(1,1)~ và đi đến ô ~(H, W)~ bằng cách di chuyển liên tục sang phải hoặc xuống dưới tới các ô trống liền kề.
Hãy tìm số cách mà Taro có thể đi từ ô ~(1,1)~ đến ô ~(H, W)~ và in kết quả dưới dạng modulo của ~10^9 + 7~
Input
- Dòng đầu chứa ba số nguyên ~H, W~ và ~N~ lần lượt là số hàng, số cột và số ô có chướng ngại vật.
- ~N~ dòng tiếp theo mỗi dòng chứa hai số nguyên ~r_i~, ~c_i~ là toạ độ của chướng ngại vật ~i~.
Giới hạn:
- ~2 \le H, W \le 10^5~
- ~1 \le N \le 3000~
- ~1 \le r_i \le H~
- ~1 \le c_i \le W~
- Tất cả các ô ~(r_i, c_i)~ là đôi một phân biệt.
Output
Số cách đi từ ô ~(1,1)~ đến ô ~(H, W)~ dưới dạng modulo của ~10^9 + 7~
Sample 1
Input
3 4 2
2 2
1 4
Output
3
Có ~3~ cách đi như hình sau:

Sample 2
Input
5 2 2
2 1
4 2
Output
0
Không có đường đi nào.
Sample 3
Input
5 5 4
3 1
3 5
1 3
5 3
Output
24
Sample 4
Input
100000 100000 1
50000 50000
Output
123445622
Note
Hãy đảm bảo kết quả in ra dưới dạng modulo của ~10^9 + 7~.
Điểm: 100
Có ~N~ hòn đá được đánh số từ 1 tới ~N~. Hòn đá thứ ~i~ ~(1 \le i \le N)~ có chiều cao ~h_i~. Ngoài ra ta có ~h_1 < h_2 < ... < h_n~.
Có một chú ếch khởi đầu ở hòn đá thứ ~1~ và nó sẽ lặp lại các hành động như sau để đến được hòn đá thứ ~N~:
- Nếu nó đang ở hòn đá ~i~, nó có thể nhảy đến bất kì hòn đá: ~i + 1, i + 2, ... N~ và mất chi phí là ~(h_j - h_i)^2 + C~ với ~j~ là hòn đá mà nó nhảy đến.
Hãy tìm chi phí nhỏ nhất có thể để chú ếch đến được hòn đá thứ ~N~.
Input
- Dòng đầu chứa hai số nguyên ~N~ và ~C ~ lần lượt là số viên đá và hệ số chi phí.
- Dòng tiếp theo chứa ~N~ số nguyên lần lượt là chiều cao của các hòn đá.
Giới hạn:
- ~1 \leq N \leq 2 \times 10^5~
- ~1 \leq C \leq 2 \times 10^{12}~
- ~1 \leq h_1 < h_2 < ... < h_n \leq 10^6~
Output
Ghi ra chi phí nhỏ nhất có thể.
Sample 1
Input 1
5 6
1 2 3 4 5
Output 1
20
Nếu chú ếch nhảy lần lượt lên các hòn đá ~1 \rightarrow 3 \rightarrow 5~ thì chi phí sẽ là: ~((3-1) ^ 2 + 6) + ((5-3)^2 + 6) = 20~.
Sample 2
Input 2
2 1000000000000
500000 1000000
Output 2
1250000000000
Sample 3
Input 3
8 5
1 3 4 5 10 11 12 13
Output 3
62
Nếu chú ếch nhảy lần lượt lên các hòn đá ~1 \rightarrow 2 \rightarrow 4 \rightarrow 5 \rightarrow 8~ thì chi phí sẽ là: ~((3-1) ^ 2 + 5) + ((5-3) ^ 2 + 5) + ((10-5) ^ 2 + 5) + ((13-10) ^ 2 + 5) = 62~.
Note
Kết quả có thể vượt quá kiểu số nguyên 32 bit.