Atcoder Educational DP Contest V - Subtree
View as PDF
Cây là đồ thị vô hướng, liên thông và không có chu trình. Một cây ~N~ đỉnh sẽ có ~(N - 1)~ cạnh. Cho một cây có ~N~ đỉnh, các đỉnh được đánh số ~1, 2, ..., N~. Cạnh thứ ~i~ ~(1 \le i \le (N - 1))~ kết nối 2 đỉnh ~x_{i}~ và ~y_{i}~.
Taro quyết định tô mỗi đỉnh của cây bởi một trong hai màu trắng hoặc đen, sao cho với hai đỉnh được tô đen bất kì, tất cả các đỉnh trên đường đi giữa hai đỉnh đó cũng được tô đen.
Bạn được cho một số nguyên dương ~M~. Với mỗi ~v~ ~(1 \le v \le N)~, hãy trả lời câu hỏi dưới đây:
Giả sử đỉnh ~v~ đã được tô màu đen, có bao nhiêu cách tô ~(n - 1)~ đỉnh còn lại để thỏa mãn điều kiện trên? Do đáp án có thể rất lớn, in ra kết quả modulo ~M~.
Input
Dòng đầu tiên chứa 2 số ~N~ và ~M~ - số đỉnh và modulo.
Dòng thứ ~i~ trong ~(N - 1)~ dòng tiếp theo chứa ~2~ số ~x_{i}~ và ~y_{i}~ - ~2~ đỉnh được nối bởi cạnh thứ ~i~.
Output
In ra ~N~ dòng, dòng thứ ~i~ in ra đáp án cho câu hỏi trên với đỉnh ~i~ theo modulo ~M~.
Giới hạn
- Tất cả các giá trị trong input là số nguyên.
- ~1 \le N \le 10^5~
- ~2 \le M \le 10^9~ (lưu ý rằng ~M~ không nhất thiết phải là số nguyên tố)
- ~1 \le x_{i}, y_{i} \le N~ ~(1 \le i \le (N - 1))~
- Đồ thị đã cho là cây.
Sample Input 1
3 100
1 2
2 3
Sample Output 1
3
4
3
Sample Input 2
4 100
1 2
1 3
1 4
Sample Output 2
8
5
5
5
Sample Input 3
1 100
Sample Output 3
1
Sample Input 4
10 2
8 5
10 8
6 5
1 5
4 8
2 10
3 6
9 2
1 7
Sample Output 4
0
0
1
1
1
0
1
0
1
1
Giải thích test đề thứ nhất
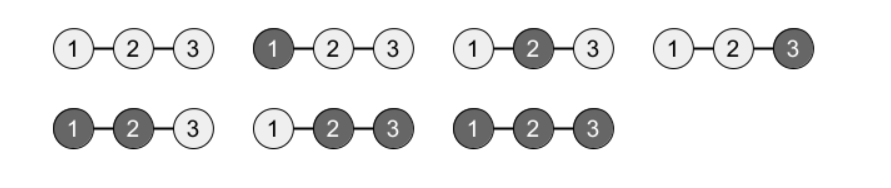
Trên đây là tất cả những cách tô màu thỏa mãn điều kiện đề bài. (Cách tô đỉnh ~1~ và ~3~ đen không thỏa mãn do đồ thị tạo bởi ~2~ đỉnh ~1~ và ~3~ không liên thông)
Trong ~7~ cách trên, có
- ~3~ cách có đỉnh ~1~ được tô màu đen
- ~4~ cách có đỉnh ~2~ được tô màu đen
- ~3~ cách có đỉnh ~3~ được tô màu đen
Comments
This comment is hidden due to too much negative feedback. Show it anyway.