Atcoder Educational DP Contest Y - Grid 2
Xem dạng PDFCó một lưới ô vuông gồm ~H~ hàng và ~W~ cột. Toạ độ ~(i, j)~ biểu thị cho ô vuông ở hàng ~i~ từ trên xuống và cột ~j~ từ trái sang. Trong lưới ô vuông có ~N~ ô ~(r_1,c_1), (r_2,c_2), ...(r_n,c_n)~ là những ô có chướng ngại vật, ngoài những ô này ra tất cả các ô còn lại là các ô trống có thể đi được. Lưới ô vuông đảm bảo rằng ô ~(1,1)~ và ô ~(H, W)~ là ô trống.
Taro sẽ bắt đầu ở ô ~(1,1)~ và đi đến ô ~(H, W)~ bằng cách di chuyển liên tục sang phải hoặc xuống dưới tới các ô trống liền kề.
Hãy tìm số cách mà Taro có thể đi từ ô ~(1,1)~ đến ô ~(H, W)~ và in kết quả dưới dạng modulo của ~10^9 + 7~
Input
- Dòng đầu chứa ba số nguyên ~H, W~ và ~N~ lần lượt là số hàng, số cột và số ô có chướng ngại vật.
- ~N~ dòng tiếp theo mỗi dòng chứa hai số nguyên ~r_i~, ~c_i~ là toạ độ của chướng ngại vật ~i~.
Giới hạn:
- ~2 \le H, W \le 10^5~
- ~1 \le N \le 3000~
- ~1 \le r_i \le H~
- ~1 \le c_i \le W~
- Tất cả các ô ~(r_i, c_i)~ là đôi một phân biệt.
Output
Số cách đi từ ô ~(1,1)~ đến ô ~(H, W)~ dưới dạng modulo của ~10^9 + 7~
Sample 1
Input
3 4 2
2 2
1 4
Output
3
Có ~3~ cách đi như hình sau:
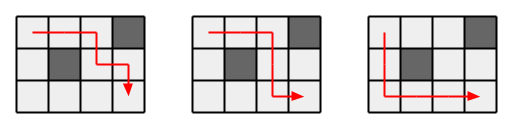
Sample 2
Input
5 2 2
2 1
4 2
Output
0
Không có đường đi nào.
Sample 3
Input
5 5 4
3 1
3 5
1 3
5 3
Output
24
Sample 4
Input
100000 100000 1
50000 50000
Output
123445622
Note
Hãy đảm bảo kết quả in ra dưới dạng modulo của ~10^9 + 7~.
Bình luận
include <bits/stdc++.h> không dùng được DP lưới đâu ae cẩn thận nhé
using namespace std;
static const long long MOD = 1e9+7; static const int MAX = 200000;
long long fact[MAX+1], invfact[MAX+1];
long long powmod(long long a, long long b) { long long res = 1; while (b) { if (b & 1) res = res * a % MOD; a = a * a % MOD; b >>= 1; } return res; }
long long C(int n, int k) { if (k < 0 || k > n) return 0; return fact[n] * invfact[k] % MOD * invfact[n-k] % MOD; }
int main() { ios::syncwithstdio(false); cin.tie(nullptr); int H, W, N; cin >> H >> W >> N; vector<pair> p(N+1); for (int i = 0; i < N; i++) { cin >> p[i].first >> p[i].second; } p[N] = {H, W}; sort(p.begin(), p.end()); int MAXN = H + W; fact[0] = 1; for (int i = 1; i <= MAXN; i++) fact[i] = fact[i-1] * i % MOD; invfact[MAXN] = powmod(fact[MAXN], MOD-2); for (int i = MAXN; i > 0; i--) invfact[i-1] = invfact[i] * i % MOD; vector<long long> dp(N+1); for (int i = 0; i <= N; i++) { int r = p[i].first; int c = p[i].second; dp[i] = C(r + c - 2, r - 1); for (int j = 0; j < i; j++) { int r2 = p[j].first; int c2 = p[j].second; if (r2 <= r && c2 <= c) { long long ways = C((r - r2) + (c - c2), r - r2); dp[i] = (dp[i] - dp[j] * ways % MOD + MOD) % MOD; } } } cout << dp[N]; return 0; }</pair>