Cho đồ thị có hướng ~G~ có ~N~ đỉnh, được đánh số từ ~1~ tới ~N~, dưới dạng ma trận kề ~a~ là một bảng gồm ~N~ hàng và ~N~ cột.

Với mỗi cặp số ~i~ và ~j~ ~(1 \le i,j \le N)~, số nguyên ~a_{i,j}~ thể hiện rằng có tồn tại hay không một cạnh có hướng từ đỉnh ~i~ tới đỉnh ~j~. Nếu ~a_{i,j} = 1~, thì tồn tại một cạnh có hướng từ đỉnh ~i~ tới đỉnh ~j~; còn nếu ~a_{i,j} = 0~ thì không tồn tại cạnh đó.

Hãy đếm số lượng đường đi khác nhau có độ dài ~K~ trong đồ thị ~G~, chia lấy số dư cho ~10^9 + 7~. Những con đường đi qua một cạnh nhiều lần cũng sẽ được tính.

Input

Dòng đầu tiên chứa hai số nguyên ~N\,(1 \le N \le 50)~ và ~K\,(1 \le K \le 10^{18})~.

~N~ dòng tiếp theo, mỗi dòng chứa ~N~ số nguyên ~a_{i,j}\,(a_{i,j} \in \left \{ 0, 1 \right \}~, ~a_{i, i} = 0)~.

Output

In ra số lượng đường đi khác nhau có độ dài ~K~ trong đồ thị ~G~.

Sample 1

Input

4 2
0 1 0 0
0 0 1 1
0 0 0 1
1 0 0 0

Output

6

Giải thích

Đồ thị ~G~ trông như sau:

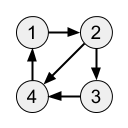
Có sáu đường đi có độ dài ~2~ là:

• ~1 \rightarrow 2 \rightarrow 3~
• ~1 \rightarrow 2 \rightarrow 4~
• ~2 \rightarrow 3 \rightarrow 4~
• ~2 \rightarrow 4 \rightarrow 1~
• ~3 \rightarrow 4 \rightarrow 1~
• ~4 \rightarrow 1 \rightarrow 2~

Sample 2

Input

3 3
0 1 0
1 0 1
0 0 0

Output

3

Giải thích

Đồ thị ~G~ trông như sau:

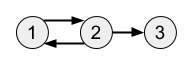
Có ba đường đi có độ dài ~3~ là:

• ~1 \rightarrow 2 \rightarrow 1 \rightarrow 2~
• ~2 \rightarrow 1 \rightarrow 2 \rightarrow 1~
• ~2 \rightarrow 1 \rightarrow 2 \rightarrow 3~

Sample 3

Input

6 2
0 0 0 0 0 0
0 0 1 0 0 0
0 0 0 0 0 0
0 0 0 0 1 0
0 0 0 0 0 1
0 0 0 0 0 0

Output

1

Giải thích

Đồ thị ~G~ trông như sau:

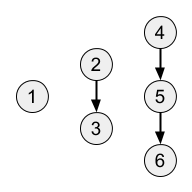
Có đúng một đường đi có độ dài ~2~ là:

• ~4 \rightarrow 5 \rightarrow 6~

Sample 4

Input

1 1
0

Output

0

Sample 5

Input

10 1000000000000000000
0 0 1 1 0 0 0 1 1 0
0 0 0 0 0 1 1 1 0 0
0 1 0 0 0 1 0 1 0 1
1 1 1 0 1 1 0 1 1 0
0 1 1 1 0 1 0 1 1 1
0 0 0 1 0 0 1 0 1 0
0 0 0 1 1 0 0 1 0 1
1 0 0 0 1 0 1 0 0 0
0 0 0 0 0 1 0 0 0 0
1 0 1 1 1 0 1 1 1 0

Output

957538352