Atcoder Educational DP Contest H - Grid 1

View as PDF
Submit solution
Points: 0.20 (partial)
Time limit: 2.0s
Memory limit: 1G
Input: stdin
Output: stdout
Suggester:
takerevenge
Problem source:
Atcoder Educational DP Contest
Problem type
Allowed languages
C, C++, Go, Java, Kotlin, Pascal, PyPy, Python, Rust, Scratch

Cho lưới hình chữ nhật gồm ~H~ hàng và ~W~ cột. Ô ~(i,j)~ được định nghĩa là ô vuông giao giữa hàng thứ ~i~ (từ trên xuống dưới) và cột thứ ~j~ (từ trái qua phải).

Mỗi ô vuông ~(i,j)~ ~(1 \leq i \leq H, 1 \leq j \leq W)~ được biểu diễn bởi 1 kí tự ~a_{i,j}~. Nếu ~a_{i,j}~ là ., ô ~(i,j)~ là một ô rỗng. Ngược lại, nếu ~a_{i,j}~ là #, ô ~(i,j)~ chứa vật cản.

Taro sẽ bắt đầu từ ô ~(1,1)~ đi tới ô ~(H,W)~. Mỗi bước đi, Taro chỉ có thể có di chuyển từ ô hiện tại tới ô liền kề bên phải hoặc ô liền kề phía dưới, với điều kiện ô đó phải là một ô rỗng.

Xác định số đường đi mà Taro có thể đi từ ô ~(1,1)~ tới ô ~(H,W)~. Đáp án có thể rất lớn, vì vậy chỉ in ra phần dư của nó khi chia cho ~10^9 + 7~.

Input

  • Dòng đầu tiên chứa hai số nguyên ~H~ và ~W~, lần lượt là số hàng và số cột của lưới. ~(2 \leq H, W \leq 1000)~

  • Dòng thứ ~i~ trong số ~H~ dòng tiếp theo chứa ~W~ kí tự, lần lượt là ~a_{i,1}....a_{i,W}~.

Đảm bảo rằng hai ô ~(1,1)~ và ~(H,W)~ luôn là ô rỗng.

Output

Gồm một số nguyên duy nhất là phần dư của số đường đi thỏa mãn mà Taro có thể đi khi chia cho ~10^9 + 7~.

Sample 1

Input
3 4
...#
.#..
....
Output
3
Giải thích

Có ~3~ cách đi như hình sau:

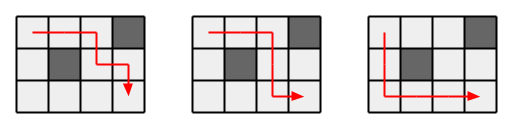
Sample 2

Input
5 2
..
#.
..
.#
..
Output
0
Giải thích

Không có bất cứ cách đi nào thỏa mãn.

Sample 3

Input
5 5
..#..
.....
#...#
.....
..#..
Output
24

Sample 4

Input
20 20
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
Output
345263555

Comments

Please read the guidelines before commenting.


  • -1
    hanguyen140210  commented on Jan. 6, 2026, 7:44 a.m.

    include<bits/stdc++.h>

    using namespace std;

    define vec vector

    define ll long long

    int i,j; int main(){ iosbase::syncwith_stdio(0); cin.tie(0);cout.tie(0); int n,m;cin>>n>>m; vec<vec>a(n+1,vec<char>(m+1)); vec<vec>dp(n+1,vec<ll>(m+1,0)); for(i=1;i<=n;i++){ for(j=1;j<=m;j++)cin>>a[i][j]; } dp[1][1]=1; for(i=1;i<=n;i++){ for(j=1;j<=m;j++){ if(i==1 && j==1) continue; if(a[i][j]=='#')continue; else { dp[i][j]=(dp[i-1][j]+dp[i][j-1])%1000000007; } } } cout<<dp[n][m]; }</vec></vec>


  • -1
    vominhmanh10  commented on Nov. 2, 2025, 3:59 a.m.

    dp đếm

    import sys
input = sys.stdin.read
mod = 10**9 + 7
def main():
    dp = [[0] * m for _ in range(n)]
    dp[0][0] = 1
    for i in range(1, n):
        if a[i][0] == '.': dp[i][0] = dp[i - 1][0]
    for i in range(1, m):
        if a[0][i] == '.': dp[0][i] = dp[0][i - 1]
    for i in range(1, n):
        for j in range(1, m):
            if a[i][j] == '.':
                dp[i][j] = (dp[i - 1][j] + dp[i][j - 1]) % mod
    return dp[n - 1][m - 1]
data = input().split()
n, m = int(data[0]), int(data[1])
a = data[2:]
print(main())

  • 0
    ChiPhatNguyen  commented on Aug. 15, 2025, 5:15 p.m.

    bai nay dung Grid dp

    code vi du: code


  • -7
    THPTHD_Hieu  commented on May 15, 2025, 2:05 a.m.

    This comment is hidden due to too much negative feedback. Show it anyway.


    • 1
      nmk05022006  commented on Sept. 30, 2025, 9:38 a.m.

      ơn cảm


    • 1
      RussVN123  commented on May 15, 2025, 3:55 a.m.

      cảm ơn ạ


  • -8
    vuongbankien012  commented on Sept. 3, 2024, 5:54 a.m.

    This comment is hidden due to too much negative feedback. Show it anyway.


  • -143
    accve4  commented on Sept. 26, 2021, 12:48 p.m.

    This comment is hidden due to too much negative feedback. Show it anyway.