Cho điểm ~(x, y)~ có tọa độ nguyên trong hệ tọa độ Descartes. Tìm góc của điểm đó trong hệ tọa độ cực.

Input

Một dòng duy nhất chứa 2 số nguyên ~x, y~ (~|x|, |y| < 10^9~) — tọa độ của điểm.

Output

Một số thực duy nhất trong khoảng ~[0, 2\pi)~ - đáp án bài toán.

Đáp án được coi là đúng khi có sai số không quá ~10^{-6}~.

Sample Input 1

3 4

Sample Output 1

0.9272952180

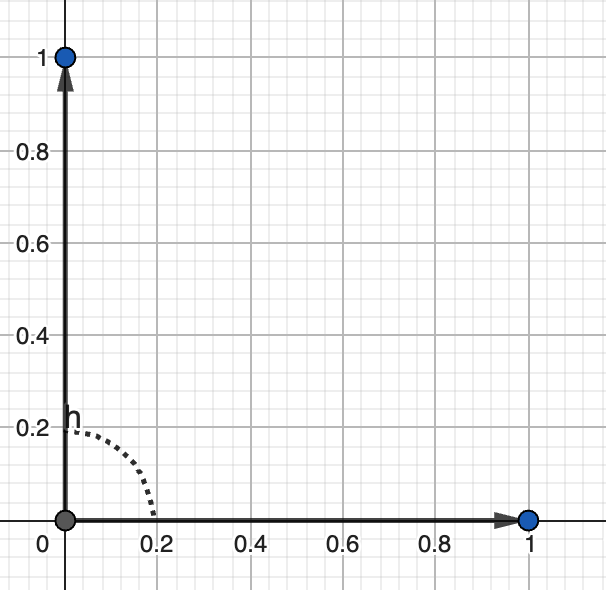
Cho hai điểm ~(x_0, y_0), (x_1, y_1)~ có tọa độ nguyên trong hệ tọa độ Descartes. Tìm góc modulo ~\pi~ giữa hai vector biểu diễn bởi hai điểm đó trong hệ tọa độ cực.

Input

Dòng đầu tiên chứa hai số nguyên thể hiện tọa độ của ~2~ điểm ~(x_0, y_0)~.

Dòng đầu hai chứa hai số nguyên thể hiện tọa độ của ~2~ điểm ~(x_1, y_1)~.

Output

Một số thực duy nhất trong khoảng ~[0, \pi]~ - đáp án bài toán.

Đáp án được coi là đúng khi có sai số không quá ~10^{-6}~.

Sample Input 1

0 1
1 0

Sample Output 1

1.570796327

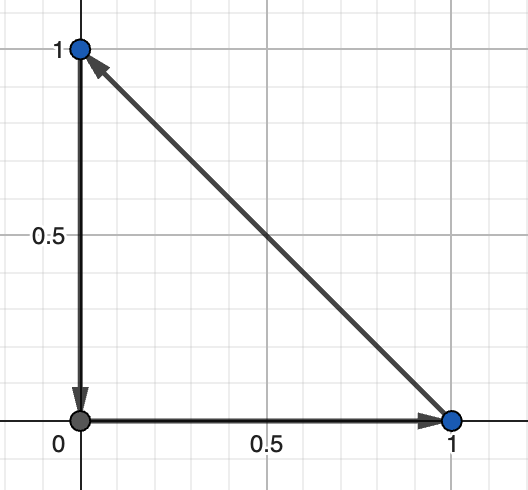
Cho đa giác lồi gồm ~n~ đỉnh, đỉnh thứ ~i~ (ngược chiều kim đồng hồ) có tọa độ ~(x_i, y_i)~. Tính diện tích của đa giác.

Input

Dòng đầu tiên gồm số nguyên dương ~n~ (~1 \le n \leq 10^5~) — số đỉnh của đa giác lồi.

~n~ dòng tiếp theo, mỗi dòng gồm 2 số nguyên ~x_i, y_i~ (~|x|, |y| \leq 10^9~).

Các điểm được sắp xếp theo thứ tự ngược chiều kim đồng hồ.

Output

In ra một số duy nhất là diện tích của đa giác đã cho.

Đáp án được coi là đúng khi có sai số không quá ~10^{-6}~.

Sample Input 1

3
0 0
1 0
0 1

Sample Output 1

0.500

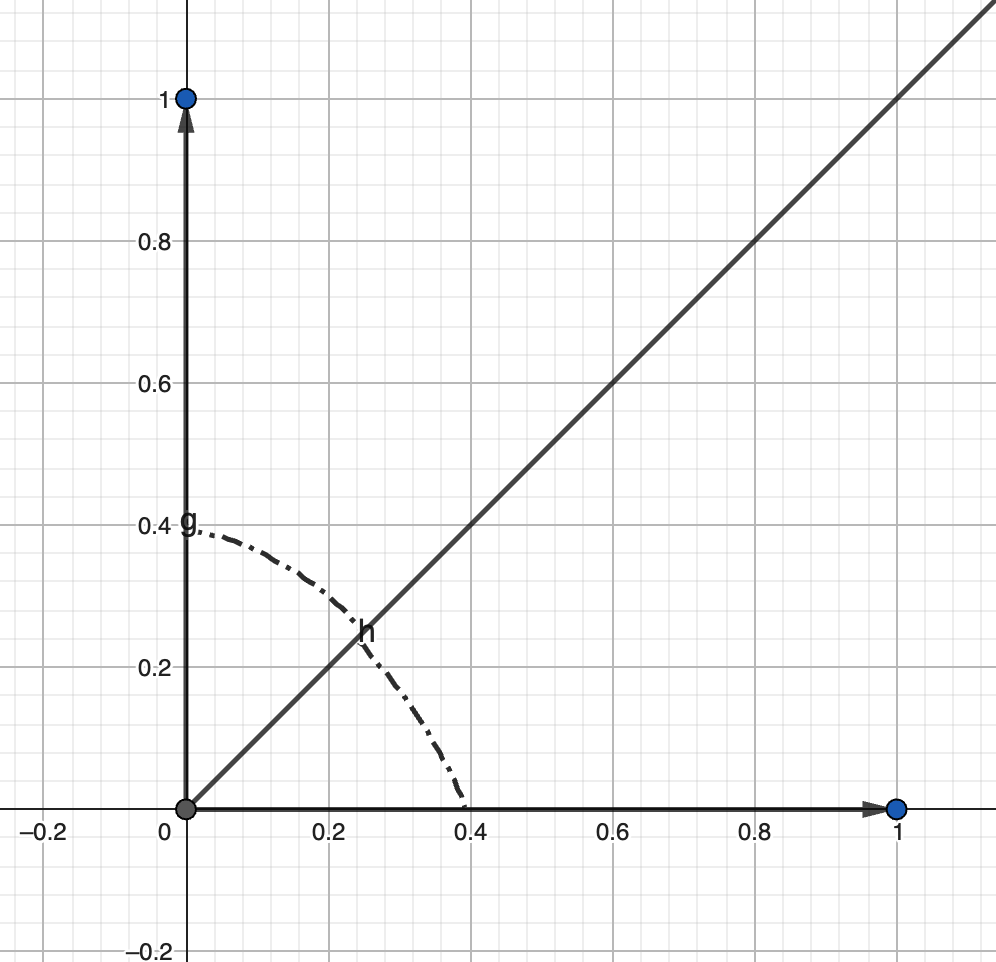
Cho 3 điểm ~X, Y, Z~ có tọa độ nguyên. Tìm phương trình của đường phân giác của góc ~\widehat{YXZ}~.

Input

Tọa độ của 3 điểm X, Y, Z trong khoảng ~[-10^9, 10^9]~, mỗi điểm trên một dòng.

Output

Một dòng duy nhất chứa 3 số thực ~a, b, c~ (~-10^{18} \le a, b, c \le 10^{18})~, biểu diễn đường thẳng có phương trình ~ax + by + c = 0~.

Đáp án được coi là đúng khi có sai số không quá ~10^{-6}~.

Sample Input 1

0 0
0 1
1 0

Sample Output 1

1.000000000 -1.000000000 0.000000000

Trên hệ trục tọa độ ~Oxy~, cho một điểm ~A~ có tọa độ nguyên ~(x, y)~ và một đường thẳng ~d~ có phương trình là ~Ax+By+C=0~. Hãy tính khoảng cách từ điểm ~A~ đến đường thẳng ~d~.

Input

Gồm các số nguyên ~x, y, A, B, C~ nằm trên cùng ~1~ dòng.

Output

Gồm một dòng duy nhất là khoảng cách từ điểm ~A~ đến đường thẳng ~d~.

Đáp án được tính là đúng nếu sai số không quá ~10^{-6}~.

Sample Input 1

1 1 1 1 -1

Sample Output 1

0.70711

Trên hệ trục tọa độ ~Oxy~, cho một điểm ~A~ có tọa độ nguyên ~(x_A, y_A)~ và một đường thẳng ~d~ đi qua ~2~ điểm ~B(x_B, y_B)~ và ~C(x_C, y_C)~. Hãy tìm khoảng cách từ điểm ~A~ đến đường thẳng ~d~.

Input

Gồm các số nguyên ~x_A, y_A, x_B, y_B, x_C, y_C~ nằm trên cùng ~1~ dòng.

Output

Gồm một dòng duy nhất là khoảng cách từ điểm ~A~ đến đường thẳng ~d~.

Đáp án được tính là đúng nếu sai số không quá ~10^{-6}~.

Sample Input 1

1 1 0 0 2 0

Sample Output 1

1.00000

Trên hệ trục tọa độ ~Oxy~, cho một điểm ~A~ có tọa độ nguyên ~(x_A, y_A)~ và một tia ~BC~ có gốc là ~B~, kéo dài về phía ~BC~ với ~B(x_B, y_B)~, ~C(x_C, y_C)~. Hãy tính khoảng cách từ điểm ~A~ đến tia ~BC~.

Input

Gồm các số nguyên ~x_A, y_A, x_B, y_B, x_C, y_C~ nằm trên cùng ~1~ dòng.

Output

Gồm một dòng duy nhất là khoảng cách từ điểm ~A~ đến tia ~BC~.

Đáp án được tính là đúng nếu sai số không quá ~10^{-6}~.

Sample Input 1

2 1 1 1 0 2

Sample Output 1

1.0

Cho một điểm ~p~ và một đoạn thẳng ~L~, hãy tìm khoảng cách giữa điểm ~p~ và đoạn thẳng ~L~ đó.

Input

Dòng đầu tiên gồm hai số nguyên dương ~x_1~ và ~y_1~ (~-10^9 \le x_1, y_1 \le 10^9~) - toạ độ điểm ~p~.

Dòng thứ hai gồm bốn số nguyên dương ~x_2, y_2, x_3, y_3~ (~-10^9 \le x_2, y_2, x_3, y_3 \le 10^9~) lần lượt là toạ độ của hai điểm đầu mút của đoạn thẳng ~L~.

Output

Gồm một dòng duy nhất là khoảng cách từ điểm ~p~ đến đoạn thẳng ~L~.

Đáp án được tính là đúng nếu sai số không quá ~10^{-6}~.

Sample Input 1

0 4
2 3 2 5

Sample Output 1

2.000000

Cho hai đoạn thẳng ~L_1~ và ~L_2~, hãy tìm khoảng cách giữa đoạn thẳng ~L_1~ và đoạn thẳng ~L_2~ đó.

Input

Dòng đầu tiên gồm bốn số nguyên dương ~x_1, y_1, x_2, y_2~ (~-10^9 \le x_1, y_1, x_2, y_2 \le 10^9~) lần lượt là toạ độ của hai điểm đầu mút của đoạn thẳng ~L_1~.

Dòng thứ hai gồm bốn số nguyên dương ~x_3, y_3, x_4, y_4~ (~-10^9 \le x_3, y_3, x_4, y_4 \le 10^9~) lần lượt là toạ độ của hai điểm đầu mút của đoạn thẳng ~L_2~.

Output

Gồm một dòng duy nhất là khoảng cách từ đoạn thẳng ~L_1~ đến đoạn thẳng ~L_2~.

Đáp án được tính là đúng nếu sai số không quá ~10^{-6}~.

Sample Input 1

1 1 2 2
2 1 3 0

Sample Output 1

0.707107

Cho hai đường thẳng ~L_1~ và ~L_2~ không song song, hãy tìm giao điểm của hai đường thẳng này.

Input

Dòng đầu tiên gồm ba số nguyên dương ~a_1, b_1, c_1~ (~-10^9 \le a_1, b_1, c_1 \le 10^9~) - lần lượt là các hệ số của đường thẳng ~(L_1)~ ~a_1 x + b_1y + c_1 = 0~.

Dòng thứ hai gồm ba số nguyên dương ~a_2, b_2, c_2~ (~-10^9 \le a_2, b_2, c_2 \le 10^9~) - lần lượt là các hệ số của đường thẳng ~(L_2)~ ~a_2 x + b_2y + c_2 = 0~.

Output

In ra hai số nguyên dương là toạ độ ~x~ và ~y~ của giao điểm hai đường thẳng ~L_1~ và ~L_2~.

Đáp án được tính là đúng nếu sai số không quá ~10^{-6}~.

Sample Input 1

1 1 -1
1 -1 0

Sample Output 1

0.500000 0.500000

Cho ~4~ số nguyên ~x_1, y_1, x_2, y_2~ lần lượt là toạ độ đầu và cuối của một vector. Hãy tìm độ dài của vector này.

Input

Một dòng duy nhất chứa ~4~ số nguyên ~x_1, y_1, x_2, y_2~ (~|x_1|, |y_1|, |x_2|, |y_2| \le 10^9~).

Output

In ra một số nguyên duy nhất là độ dài của vector này.

Đáp án được coi là đúng khi có sai số không quá ~10^{-6}~.

Sample Input 1

1 1 2 2

Sample Output 1

1.414214

Cho ~2~ điểm ~A,B~ trên trục tọa độ ~Oxy~, hãy in ra phương trình đường thẳng đi qua ~2~ điểm đó dưới dạng ~ax + by + c = 0~.

Input

• Gồm một dòng chứa tọa độ của hai điểm ~A~ và ~B~ ~(0 \le |x_A|,|y_A|,|x_B|,|y_B| \le 10^6)~.

Output

• Gồm một dòng chứa ~3~ số nguyên dương ~a,b,c~ miêu tả phương trình đường thẳng đi qua ~2~ điểm ~A~ và ~B~.

• Các số ~a,b,c~ phải nằm trong khoảng ~[-2 \cdot 10^{12},2 \cdot 10^{12}]~

Sample Input 1

1 2 3 1

Sample Output 1

-1 -2 5

Trên trục tọa độ ~Oxy~, hãy xác định một đường thẳng có dạng ~ax + by + c = 0~, biết đường thẳng đó đi qua điểm ~A~ và có vector pháp tuyến ~(u, v)~.

Input

• Gồm một dòng chứa tọa độ nguyên của điểm ~A~ và vector pháp tuyến ~(u,v)~ của đường thẳng ~(0 \le |x_A|,|y_A|,u,v \le 10^6)~

Output

• Gồm một dòng chứa ~3~ số nguyên ~a,b,c~ miêu tả phương trình đường thẳng đi qua điểm ~A~ và có vector pháp tuyến là ~(u,v)~.

• Các số ~a,b,c~ phải thuộc trong khoảng ~[-2 \cdot 10^{12},2\cdot 10^{12}]~

• Đáp án được coi là đúng khi có sai số không quá ~10^{-6}~.

Sample Input 1

1 2 3 1

Sample Output 1

3 1 -5

Trên trục tọa độ ~OXY~, cho một đường thẳng có dạng ~ax + by + c = 0~ và một giá trị ~R~, hãy tìm hai đường thẳng khác nhau song song với đường thẳng đã cho và cách đường thẳng đó độ dài bằng ~R~.

Input

• Gồm một dòng chứa ~4~ số ~a,b,c,R~ miêu tả đường thẳng và giá trị ~R~ ~(0 \le |a|,|b|,|c| \le 10^6, 1 \le R \le 10^6)~.

Output

• In ra ~2~ dòng, mỗi dòng gồm ~3~ số thực ~a,b,c~ miêu tả đường thẳng song song với đường thẳng đã cho và cách đường thẳng đó độ dài bằng ~R~ ~(0 \le |a|,|b|,|c| \le 2 \cdot 10^{12})~.

• Đáp án được coi là đúng khi có sai số không quá ~10^{-6}~.

Sample Input 1

0 -1 1 1

Sample Output 1

0.0000000000 -1.0000000000 0.0000000000
0.0000000000 -1.0000000000 2.0000000000

Cho tọa độ ~(x_P, y_P)~ của điểm ~P~ và đường thẳng ~(d): Ax + By + C = 0~, kiểm tra xem ~P~ có thuộc ~(d)~ hay không.

Input

Gồm một dòng duy nhất chứa ~5~ số nguyên ~x_P, y_P, A, B, C\ (-10^9 \leq x_P, y_P, A, B, C \leq 10^9)~

• ~2~ số đầu là tọa độ của điểm ~P(x_P, y_P)~.

• ~3~ số sau là các hệ số ~A, B, C~ của đường thẳng ~(d)~.

Output

Gồm một dòng duy nhất, in ra YES nếu ~P~ nằm trên đường thẳng ~(d)~, ngược lại in ra NO.

Sample Input 1

3 7 -2 1 -1

Sample Output 1

YES

Cho tọa độ ~(x_P, y_P)~ của điểm ~P~ và một tia được xác định bởi 2 điểm - gốc ~O(x_O, y_O)~ và một điểm ~T(x_T, y_T)~ khác ~O~, kiểm tra xem ~P~ có thuộc tia ~OT~ hay không.

Input

Gồm ~6~ số nguyên ~x_P, y_P, x_O, y_O, x_T, y_T\ (-10^9 \leq x_P, y_P, x_O, y_O, x_T, y_T \leq 10^9)~.

Dữ liệu đảm bảo ~O~ và ~T~ luôn là hai điểm phân biệt ~(x_O \neq x_T~ hoặc ~y_O \neq y_T)~.

Output

Gồm một dòng duy nhất, in ra YES nếu ~P~ nằm trên tia ~OT~, ngược lại in ra NO.

Sample Input 1

1 1 0 0 2 2

Sample Output 1

YES

Cho tọa độ ~(x_P, y_P)~ của điểm ~P~ và một đoạn thẳng được xác định bởi 2 điểm ~A(x_A, y_A)~ và ~B(x_B, y_B)~ khác ~A~, kiểm tra xem ~P~ có thuộc đoạn thẳng ~AB~ hay không.

Input

Gồm ~6~ số nguyên ~x_P, y_P, x_A, y_A, x_B, y_B\ (-10^9 \leq x_P, y_P, x_A, y_A, x_B, y_B \leq 10^9)~.

Dữ liệu đảm bảo ~A~ và ~B~ luôn là hai điểm phân biệt ~(x_A \neq x_B~ hoặc ~y_A \neq y_B)~.

Output

Gồm một dòng duy nhất, in ra YES nếu ~P~ nằm trên đoạn thẳng ~AB~, ngược lại in ra NO.

Sample Input 1

2 3 0 1 6 7

Sample Output 1

YES

Cho hai điểm và một đường thẳng. Kiểm tra xem hai điểm cùng phía so với đường thẳng không.

Input

Một dòng duy nhất gồm các số nguyên ~x_0~, ~y_0~, ~x_1~, ~y_1~, ~a~, ~b~, ~c~ ~(-10 \leq x_i, y_i \leq 10, -8000 \leq a, b, c \leq 8000~), trong đó hai điểm đã cho có toạ độ ~(x_0, y_0)~ và ~(x_1, y_1)~, và phương trình đường thẳng là ~ax + by + c = 0~. Dữ liệu đầu vào đảm bảo hai điểm không nằm trên đường thẳng.

Output

In ra YES nếu hai điểm nằm cùng phía so với đường thẳng, nếu không in ra NO.

Sample Input 1

0 0 2 4 2 -1 -1

Sample Output 1

YES

Sample Input 2

0 1 1 0 -4 0 8

Sample Output 2

YES

Sample Input 3

0 1 1 0 0 4 8

Sample Output 3

YES

Cho hai tia trên mặt phẳng, mỗi tia được xác định bởi hai điểm. Tính khoảng cách giữa hai tia (khoảng cách nhỏ nhất giữa hai điểm bất kỳ thuộc hai tia).

Input

Dòng thứ nhất gồm bốn số nguyên ~x_0~, ~y_0~, ~x_1~, ~y_1~, trong đó ~(x_0, y_0)~ là gốc tia thứ nhất và ~(x_1, y_1)~ là một điểm nằm trên tia thứ nhất.

Dòng thứ hai gồm bốn số nguyên ~x_2~, ~y_2~, ~x_3~, ~y_3~, trong đó ~(x_2, y_2)~ là gốc tia thứ hai và ~(x_3, y_3)~ là một điểm nằm trên tia thứ hai.

Dữ liệu đầu vào đảm bảo:

• ~x_0 \neq x_1~ hoặc ~y_0 \neq y_1~

• ~x_2 \neq x_3~ hoặc ~y_2 \neq y_3~

• ~-32768 \leq x_i, y_i \leq 32768\ \forall 0 \leq i \leq 3~.

Output

In ra một số thực duy nhất là khoảng cách cần tính.

Đáp án được chấp nhận nếu sai lệch so với đáp án chuẩn không vượt quá ~10^{-6}~.

Sample Input 1

0 0 1 0
0 1 0 2

Sample Output 1

1.000000000000000

Sample Input 2

4 5 4 6
4 2 4 1

Sample Output 2

3.000000000000000