
|
Mabư Béo đã rất vui sau khi được chứng kiến các bạn nhiệt tình giúp đỡ hắn ta trên hành trình tìm lại Bảy Viên Ngọc Rồng. Thay mặt DTL và Mabư Béo, low_ xin cảm ơn đội ngũ VNOJ đã hỗ trợ cho contest được diễn ra. Cảm ơn các bạn thí sinh đã có màn trình diễn với những trận đua sôi động, và hẹn gặp các bạn ở trong các chuyến phiêu lưu tiếp theo! ^^ |
(Proposal đề được viết bằng tiếng Anh, các setter cũng chưa có thời gian để dịch lại đa số bài cho chuẩn. Mong các bạn thông cảm :D)
A. Mabư Béo và Bài toán Đa giác
Polygon inequality: the longest side of the polygon have to be strictly smaller than sum of the rest.
Sort ~A~. Find greatest ~i~ such that ~A_i <~ sum of ~A_1~ to ~A_{i-1}~. To quickly calculate sum of first ~i~ elements in the array, use Prefix Sum.
Complexity: ~O(N * log(N))~.
B. Mabư Béo và Trò chơi Bánh quy
If ~N~ odd, the first kid that will exhaust of cookies are the one with the least amount of cookies to begin with. If there are multiple kids with the same number of minimum cookies, the kid with even indices will exhaust first, and then the odds. Then we'll consider whichever kid with the smaller index.
If ~N~ is even, only the even-indexed kid will be exhaust of cookies, as we can prove that the kid with odd index will have his number of cookies remain unchanged throughout the game. The smaller indexed kid will exhaust their cookies first.
Complexity: ~O(N)~.
C. Mabư Béo Tập Thể dục
This problem can be solved by DP.
Let ~F(i,j,k)~ be the distance the Majin Buu has traveled at time ~i~, with speed ~j~, and ~k~ energy left.
~F(i+1, j+1, k-L) = F(i,j,k) + j+1~ if ~k \ge L~ and ~j < S~
Set ~jj=max(0, j-1)~ => ~F(i+1, jj, min(k+D, C)) = F(i,j,k) + jj~
~F(i+1, j, k-K) = F(i,j,k) + j~ if ~k \ge K~.
Answer: max of all ~F(T,j,k)~.
D. Mabư Béo Trèo Cây
We solve this problem using DP.
~dp(i, k)~ - number of nodes that need rearrangement in subtree of root ~i~. ~k = true~ if ~i~ is parsed with one of its children, ~false~ if ~i~ is expected to be parsed with its parent node.
If ~i~ is a leaf (has only ~1~ connected node and not a root): ~dp(i, true) = 1~ and ~dp(i, false) = 0~.
For other ~i~: ~dp(i, true)~ and ~dp(i, false)~ will be calculated using ~dp~ information of their children.
~dp(i, true) =~ min of ~(dp(j, false) + ~ sum of ~dp(k, true)~ for every ~k \neq j)~ for every ~j~ is children of ~i~.
~dp(i, false) =~ sum of ~dp(j, true)~ for every ~j~ is children of ~i~.
Answer is ~\frac{dp(root, true)}{2}~.
E. Mabư Béo tập Gym
~N~ is prime, can be written in ~3k + 1~. Therefore, ~N~ can also be written in ~6l + 1~.
For any ~N~, we will try to construct groups where (1) all groups have size ~2~, and (2) all groups have size ~3~. Then, we'll try to mash these 2 constructive algorithm together.
(1) Case of all ~a_i = 2~: For each ~i~ from ~1~ to ~\frac{N-1}{2}~, match ~i~ with ~N - i~.
(2) Case of all ~a_i = 3~. Set ~k = \frac{N - 1}{6}~. For each ~i~ from ~1~ to ~k~, we construct two sets: ~(i, 3k - 2i + 1, n - 3k + i - 1)~, ~(3k - 2i + 2, n - 2k + i - 1, n - k + i - 1)~.
Any greater ~a_i~ can be broken down into multiple smaller subsets of two above sizes. We just need to find a way to divide weights into sets of both types. For example, if you want to make a group of ~7~ weights, you just have to take ~2~ sets of size ~2~ and ~1~ set of size ~3~.
Base on the requirement, if you need to construct ~l_2~ groups of size ~2~, and ~l_3~ groups of size ~3~ (~l_2 * 2 + l_3 * 3 = N - 1~), here is one example of how you can construct these. The way I came up with these construction for ~N~ is that when I've already know how to construct groups of ~3~ for some ~N~, I can extend the same construction to ~N + 6~, and leave out some pairs to make group of ~2~:
Step 1: Set ~k = \frac{N - 1}{6}~ and ~l = \frac{N - l_3 * 3}{6}~.
Step 2: For each ~i~ from ~1~ to ~k - l~, create 2 sets of size ~3~: ~(i, 3 * k - l - 2 * i + 1, 3 * k + l + i)~ and ~(3 * k - l - 2 * i + 2, 4 * k + i, 5 * k + l + i)~.
Step 3: We can prove that if there exist some number ~i~ that unused after steps above, ~N - i~ is also unused. Therefore, unused numbers can be grouped into ~l_2~ groups of size ~2~.
Complexity: ~O(N)~.
F. Mabư Béo Chia Bánh
Giả sử số bánh của mỗi đĩa trong đáp án là ~A_1, A_2, \ldots, A_N~. Đặt ~S_i = A_1 + A_2 + \ldots + A_i~, ta có ~A_N = M~ và điều kiện cần và đủ để thỏa mãn ~k~ vị khách là: với mỗi ~j \in [1..k]~, tồn tại ~i \in [1..N]~ sao cho ~S_i = \frac{jM}{k}~.
Do vậy, với mỗi ước ~k~ không lớn hơn ~N~ của ~M~, gọi ~G_k = \{\frac{M}{k}, \frac{2M}{k}, \ldots, \frac{kM}{k}\}~ thì điều kiện cần và đủ để tìm được dãy $A$ thỏa mãn tất cả các số ~P = \{k_1, k_2, \ldots, k_s\}~ là ~G(P) = |G_{k_1} \cup G_{k_2} \cup \ldots \cup G_{k_s}| \leq N~. Ta cần tìm tập ~P~ lớn nhất thỏa mãn điều kiện trên.
Ta có một số nhận xét sau:
- Nếu dãy ~A~ thỏa mãn ~k~ thì dãy ~A~ cũng thỏa mãn mọi ước ~k'~ của ~k~. Do đó, nếu ~k \in P~ thì ~k' \in P~.
- Giả sử ~P~ chứa tất cả các ước ~k' < k~ của ~k~ nhưng không chứa ~k~. Ta có ~G(P \cup \{k\}) = G(P) \cup G_k = G(P) \cup \{\frac{jM}{K} | 1 \leq j \leq k, gcd(k, j) = 1\}~. Suy ra ~|G(P \cup \{k\})| = |G(P)| + \phi(k)~, với ~\phi(k)~ là phi hàm Euler của ~k~.
- Với ~k'~ là ước của ~k~, ~\phi(k') \leq \phi(k)~.
Bằng những nhận xét trên, ta có thể giải bài toán bằng thuật toán tham lam như sau:
- Sắp xếp các ước ~k \leq N~ của ~M~ theo ~\phi(k)~ tăng dần, nếu bằng nhau sắp xếp theo ~k~ tăng dần.
- Lần lượt thêm các ước vào tập kết quả ~P~ sao cho ~|G(P)| \leq N~.
Lưu ý rằng đề bài yêu cầu dãy gồm đúng ~N~ số nguyên dương, do đó, nếu ~|S| = |G(P)| < N~, ta cần thêm một vài giá trị vào ~S~ sao cho ~|S| = N~.
Độ phức tạp của thuật toán là ~O(N log N)~.
G. Mabư Béo vào Đội Tuyển LoL
Đặt ~S(i)~ là xâu thoả mãn độ dài ~3^i~.
~S(0) = \texttt{a}~
Từ ~S(i)~ sinh được ~S(i + 1)~ theo quy tắc:
Ở các vị trí chẵn (đánh số từ ~0~), ~\texttt{a}~ thay bằng ~\texttt{abc}~, ~\texttt{b}~ thay bằng ~\texttt{bca}~, ~\texttt{c}~ thay bằng ~\texttt{cab}~.
Ở các vị trí lẻ, ~\texttt{a}~ thay bằng ~\texttt{cba}~, ~\texttt{b}~ bằng ~\texttt{acb}~, ~\texttt{c}~ bằng ~\texttt{bac}~.
Chứng minh tính đúng đắn bằng quy nạp.
H. Mabư Béo và Bài Luyện Tập
If we put on a directed graph and connect from ~x~ to ~p(x)~, there will be some cycles. One application of ~p~ will move from one node to the node that it is connected to.
Assuming that there are ~k~ cycles with sizes ~C_1, C_2, ..., C_k~, the formula for ~G~ is:
~G(p) = LCM(C_1, C_2, ..., C_k)~.
The problem can narrows down to:
Given ~C_1, C_2, ..., C_k~. In one move, you can do one of these:
(1) Choose ~i~, ~j~: ~1 \le i < j \le k~, replace ~C_i, C_j~ with ~C_i + C_j~. (2) Choose ~i~: ~1 \le i \le k~, replace ~C_i~ with ~C_k~ and ~C_l~ so that ~C_k + C_l = C_i~. (3) Do nothing.
And your task is to minimize ~LCM(C)~.
Set ~\phi'(n)~ = ~\phi(\sqrt{n}) + \frac{\phi(n)}{64}~, with ~\phi(x)~ is the number of primes not greater than ~x~.
Now, for every number ~x~, we convert it to a vector (for primes ~\le \sqrt{n}~) + bitset (for primes ~> \sqrt{n}~) that can contain information of ~x~'s prime factorization. So now finding ~LCM~ of two numbers can be done for about ~\phi'(n)~ operations.
To faster calculate ~LCM(C)~ when we remove some numbers, we can use RMQ.
If we choose to do (1), what we can do is to iterate every pair that can be replaced. Since there can only be maximum of about ~\sqrt{N}~ different values in ~C~, every pair we can remove from the set can be checked in ~O(N)~. For each pair, to calculate new ~LCM~ would takes around ~5 LCM~ operations (with RMQ), so we can estimate that it would take about O(~\phi'(n)*N~) to discover all possibility for (1).
If we choose to do (2), we can for each value in ~C~ to find the best split possible for every value. In other words, for value ~x~, we can iterate through every ~y~ and ~z~ so that ~y + z = x~. We'll try to remove value ~x~ from ~C~ and replace it with ~LCM(y, z)~. Of course, if there are multiple copies of ~x~ in ~C~, we can skip ~x~ because it will not optimize ~LCM(C)~. Would also take about ~O(\phi'(n)*N)~ to discover all cases.
Overall complexity: ~O(N * \phi'(n))~.
Comparing to the intended solution above, we decided to lower the constraint from original version (5e4) to let more solution passed. As long as you conceptually understand the concept of having to find LCM, you can pass this problem easily!
I. Mabư Béo chơi Đế Chế
Trước tiên, hãy thử giải phiên bản đơn giản hơn của bài toán: các tọa độ ~x_i~ và ~y_i~ đều phân biệt.
Xét một tập ~C~ những thành phố chưa bị chiếm trong một kế hoạch nào đó. Gọi ~(L, R, U)~ là những thành phố có hoành độ nhỏ nhất, hoành độ lớn nhất và tung độ lớn nhất trong các thành phố thuộc ~C~. Ta dễ thấy rằng:
- Mọi thành phố ~(x, y)~ thỏa mãn ~x_L \le x \le x_R~ và ~y \le y_U~ đều thuộc C.
- Mọi thành phố ~(x, y)~ không thỏa mãn điều kiện trên đều không thuộc C.
Do đó, mỗi bộ ~(L, R, U)~ tương ứng với tối đa một kế hoạch. Ngược lại, mỗi kế hoạch (trừ kế hoạch đánh chiếm tất cả các thành phố) tương ứng với đúng một bộ ~(L, R, U)~. Như vậy để đếm số kế hoạch, ta có thể đếm số bộ ~(L, R, U)~ tương ứng với một kế hoạch nào đó, rồi lấy kết quả cộng thêm ~1~. Điều kiện để bộ ~(L, R, U)~ thỏa mãn là:
- ~x_L \le x_U \le x_R~
- ~y_L \le y_U~, ~y_R \le y_U~
Vậy với mỗi thành phố ~U~, gọi ~left_U~ là số thành phố ~V~ thỏa mãn ~x_V \leq x_U, y_V \leq y_U~ và ~right_U~ là số thành phố ~V~ thỏa mãn ~x_V \geq x_U, y_V \leq y_U~ thì số kế hoạch sao cho ~U~ là thành phố chưa bị chiếm có tung độ lớn nhất là ~left_U \times right_U~. Ta có thể tìm ~left_U~ và ~right_U~ một cách hiệu quả bằng cấu trúc dữ liệu Fenwick Tree.
Trở lại với bài toán gốc, với mỗi tập ~C~ những thành phố chưa bị chiếm, ta cũng xét ~(x_L, x_R, y_U)~ là hoành độ nhỏ nhất, hoành độ lớn nhất và tung độ lớn nhất thuộc ~C~. Giống như ở trên, những thành phố nằm trong vùng bị giới hạn bởi những tọa độ trên đều chắc chắn thuộc ~C~, còn những thành phố nằm ngoài chắc chắn không thuộc ~C~. Tuy nhiên, những thành phố nằm "trên biên" có thể thuộc hoặc không thuộc ~C~. Do vậy, để tránh đếm lặp, với mỗi thành phố ~U~ ta sẽ đếm số tập ~C~ sao cho ~U~ là thành phố thuộc ~C~ có tung độ lớn nhất và có hoành độ lớn nhất trong những thành phố có cùng tung độ. Xét 4 trường hợp:
- ~U~ không nằm trên biên trái hoặc biên phải của ~C~.
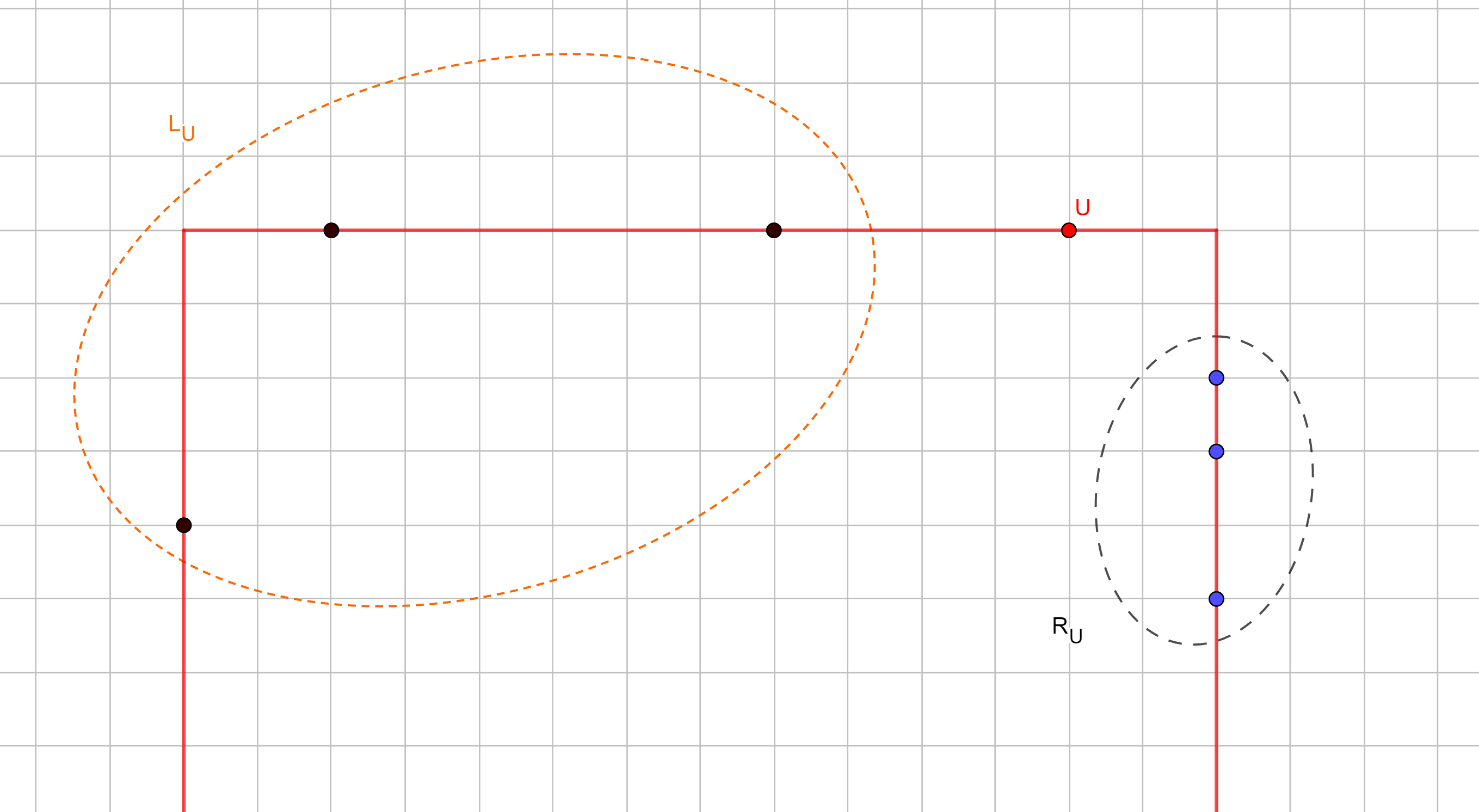 Ta gọi ~L_U~ là tập hợp (không rỗng) các thành phố nằm bên trái ~U~ trên biên của ~C~, và ~R_U~ là tập hợp (không rỗng) các thành phố nằm bên phải ~U~. Gọi ~left(U)~, ~right(U)~ là số tập ~L_U~, ~R_U~ thỏa mãn thì số cách chọn sẽ là ~left(U) \times right(U)~.
Ta gọi ~L_U~ là tập hợp (không rỗng) các thành phố nằm bên trái ~U~ trên biên của ~C~, và ~R_U~ là tập hợp (không rỗng) các thành phố nằm bên phải ~U~. Gọi ~left(U)~, ~right(U)~ là số tập ~L_U~, ~R_U~ thỏa mãn thì số cách chọn sẽ là ~left(U) \times right(U)~. - ~U~ nằm trên biên trái nhưng không nằm trên biên phải của ~C~. Gọi ~D_U~ là tập hợp (có thể rỗng) các thành phố nằm dưới ~U~ và có cùng hoành độ với ~U~ trên biên của ~C~, và ~down(U)~ là số tập ~D_U~ thỏa mãn. Số cách chọn là ~down(U) \times right(U)~.
- ~U~ nằm trên biên phải nhưng không nằm trên biên trái của ~C~. Tương tự trường hợp 2, số cách chọn là ~left(U) \times down(U)~.
- ~U~ nằm trên cả biên trái và biên phải của ~C~. Trường hợp này chỉ xảy ra khi tập ~C~ gồm các thành phố có hoành độ bằng nhau, số cách chọn là ~down(U)~.
Cuối cùng, ta cần tìm cách tính ~left(U)~, ~right(U)~, ~down(U)~ với mỗi thành phố ~U~. Trước tiên, gọi ~low(x, y)~ là số thành phố nằm dưới tọa độ ~(x, y)~ (nói cách khác, số thành phố ~V~ thỏa mãn ~x_V = x~ và ~y_V < y~). Dễ thấy rằng ~down(U) = 2 ^ {low(x_U, y_U)}~. Tương tự, ~right(U) = \sum_{x > x_U} (2 ^ {low(x, y_U)} - 1)~. Việc tính ~left(U)~ đòi hỏi một chút kiến thức về quy hoạch động: xét ~U'~ là thành phố gần nhất về bên trái có cùng tung độ với ~U~. Ta có thể chọn ~L_U~ theo 1 trong 3 trường hợp sau:
- Biên trái của ~L_U~ nằm bên trái ~U'~.
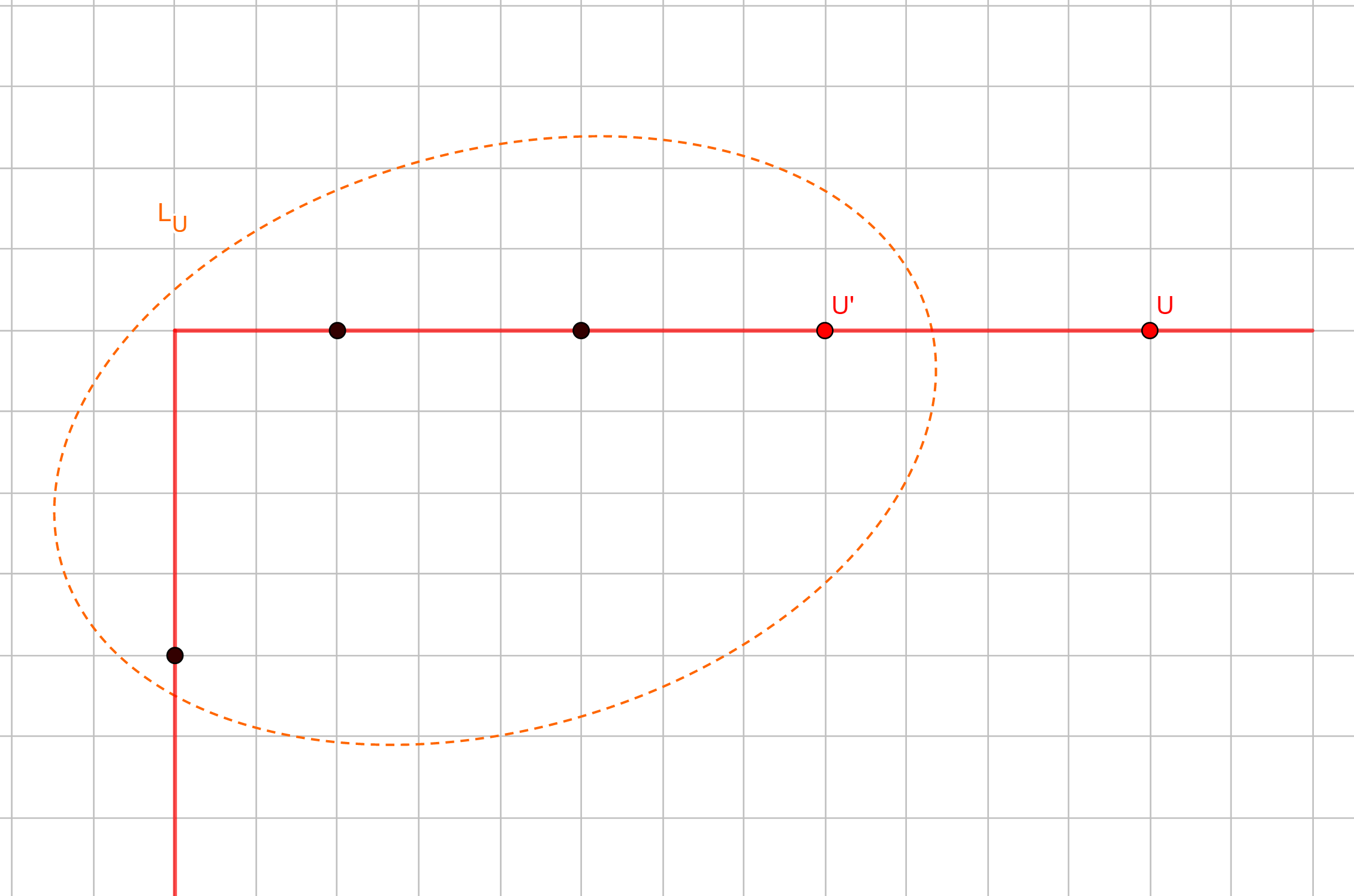 Ta có thể chọn hoặc không chọn ~U'~ nằm trong ~L_U~, do đó số cách chọn là ~2 \times left(U')~.
Ta có thể chọn hoặc không chọn ~U'~ nằm trong ~L_U~, do đó số cách chọn là ~2 \times left(U')~. - Biên trái của ~L_U~ nằm dưới ~U'~. Tương tự trường hợp trên, ta có thể chọn hoặc không chọn ~U'~ nằm trong ~L_U~, do đó số cách chọn là ~2 \times down(U') - 1~ (không tính trường hợp ~L_U~ rỗng).
- Biên trái của ~L_U~ nằm bên phải ~U'~. Do giữa ~U'~ và ~U~ không có thành phố nào cùng tung độ, biên trên của ~L_U~ chỉ chứa đúng thành phố ~U~. Do đó số cách chọn chính là số cách chọn biên trái: ~\sum_{x_U' < x < x_U} (2 ^ {low(x, y_U)} - 1)~.
Tóm lại, ~left(U) = 2 \times left(U') + 2 \times down(U') - 1 + \sum_{x_U' < x < x_U} (2 ^ {low(x, y_U)} - 1)~.
Ta có thể tính nhanh những công thức trên bằng cách duyệt các thành phố ~U~ theo thứ tự tung độ tăng dần rồi hoành độ tăng dần, sử dụng Fenwick Tree để cập nhật giá trị và tính tổng một đoạn.
Độ phức tạp của thuật toán là ~O(N log N)~.
J. Mabư Béo đi tìm Bảy Viên Ngọc Rồng
- Because ~x~ and ~y~ are independent, the partial derivatives are easy to calculate.
- We can then calculate all the local maximum / minimum, saddle points, .... Let's call these points of interest or POI.
- Let's divide the world into a grid, with each POI being a point on the grid.
- Then it's enough to do DSU on this grid, connecting each point that has height ~> c~ with a point adjacent to it on the grid.
- Proof:
- The proof has 3 part, first is proving that each region that is ~> c~ is represented by at least one POI:
- From a point ~P~ that has height ~> c~, call ~S~ the set of points that is connected to ~P~ without going to any point with height ~\le c~.
- It is clear that we can reach a local maximum of the whole function using this process:
- Because the function is continuous, if ~P~ is not a local maximum, we can clearly go to an "adjacent point" with higher height.
- Because at each time, we only go to a point with height height, we always stay above the height ~c~.
- Thus every connected region of height ~> c~ contains at least one local maximum of the whole function, and can be represented by a local maximum.
- The second part prove that the POI connected on the grid with height ~> c~ is in the same region:
- Let’s ~A~ be a POI that has height ~> c~. Let ~B~ be another POI next to ~A~.
- If ~B~ has height ~\le c~ then ~B~ is clearly not in the same region as ~A~. (It’s not in any region)
- If ~B~ has height ~> c~ then ~B~ and ~A~ are clearly in the same region because on the direct path from ~A~ to ~B~, the function only increases or decreases (because between adjacent POI, the derivative is always positive or negative along an axis).
- The third part proves that to go from a POI with height ~> c~ to another one with height ~> c~, it is always possible to just go through other POI.
- Let’s draw a path ~> c~ connect to the ~2~ POI with height ~> c~.
- Let’s say we move from one cell to another cell on the grid. We clearly cut through the shared edge between these cells.
- Because each edge of a cell is increasing toward some direction, can move out path to end in one of the 2 POI that make up that edge that has height ~> c~.
- So from the starting POI, we either move directly to an adjacent POI, or we move to the POI opposite on the same cell.
- Due to property of POI, we can see that the diagonal move can always be changed to 2 adjacent move:
- Assume diagonal move, then both point ~> c~
- If no other POI ~> c~ then on one edge, we have increasing but on the opposite edge, we have decreasing
- So from the starting POI, we can always move to an adjacent POI and still perverse the path.
- Which means that it is possible to move from any POI to any other POI in the same region only through the POI graph.
- The proof has 3 part, first is proving that each region that is ~> c~ is represented by at least one POI:
Solving for the POI requires solving the 2 partial derivatives. For degree <= 3, this is just solving a quadratic equation.
Bình luận