VNOI CUP 2023 - Vòng loại thứ ba
Điểm: 750
Máy lạnh trong căn phòng trọ mà Quang đang ở lại một lần nữa bị chảy nước. Dưới cái nóng như hỏa thiêu của tiết trời hiện nay, việc sống không có máy lạnh là đều không thể. Do đó, trong lúc chờ đợi thợ đến sửa, cậu không còn cách nào khác ngoài việc tiếp tục bật máy lạnh và lấy thau hứng nước ở những chỗ bị dột.
Ta có thể xem phần nền nhà nằm ngay dưới máy lạnh là trục số thực. Có ~n~ điểm mà máy lạnh chảy nước, điểm nước chảy thứ ~i~ có tọa độ ~x_i~. Quang có hai thau nước với chiều dài lần lượt là ~a~ và ~b~. Với thau nước có chiều dài ~l~, nếu đầu mút bên trái của thau được đặt ở tọa độ ~p~ thì thau sẽ hứng được các điểm nước chảy có tọa độ từ ~p~ đến ~p + l~ (khi đó ta nói rằng thau nước được đặt ở vị trí ~[p; p+l]~). Lưu ý rằng có thể đặt hai thau nước sao cho phần giao của chúng có độ dài lớn hơn ~0~.
Hãy giúp Quang kiểm tra xem có cách đặt hai thau nước nào mà mọi điểm nước chảy đều được hứng bởi ít nhất một thau nước không nhé.
Input
Mỗi input sẽ gồm nhiều test cases. Dòng đầu tiên của input gồm số nguyên dương ~t~ (~1 \le t \le 100~) — số test cases của bài toán. Sau đây là mô tả của các test cases.
Dòng đầu tiên của mỗi test case gồm ba số nguyên dương ~n~, ~a~, ~b~ (~1 \le n \le 100~, ~1 \le a, b \le 100~) — số điểm mà máy lạnh bị chảy nước và chiều dài của hai thau nước.
Dòng tiếp theo của mỗi test case gồm ~n~ số nguyên dương ~x_1, x_2, \dots, x_n~ (~0 \le x_1 < x_2 < \ldots < x_n \le 100~) — mô tả tọa độ của các điểm nước chảy.
Output
Với mỗi test case, in ra "YES" nếu như tồn tại một cách đặt hai thau nước sao cho mọi điểm nước chảy đều được hứng bởi ít nhất một thau, hoặc in ra "NO" trong trường hợp ngược lại.
Scoring
Số điểm nhận được nếu bạn giải thành công bài toán này là ~750~ điểm.
Sample Input 1
4
4 3 2
1 2 4 8
4 1 2
1 3 5 6
3 1 1
1 3 5
3 5 5
1 2 3
Sample Output 1
YES
YES
NO
YES
Notes
Ở ví dụ thứ nhất, hai thau nước có chiều dài lần lượt là ~3~ và ~2~. Nếu đặt hai thau nước lần lượt ở vị trí ~[1, 4]~ và ~[7, 9]~ thì các điểm chảy nước ở tọa độ ~1~, ~2~, ~4~ sẽ được hứng bởi thau thứ nhất, và điểm chảy nước ở tọa độ ~8~ sẽ được hứng bởi thau thứ hai.
Ở ví dụ thứ hai, ta có thể đặt hai thau nước lần lượt ở vị trí ~[5, 6]~ và ~[1, 3]~ thì các điểm chảy nước ở tọa độ ~5~, ~6~ sẽ được hứng bởi thau thứ nhất, và các điểm chảy nước ở tọa độ ~1~, ~3~ sẽ được hứng bởi thau thứ hai.
Ở ví dụ thứ ba, với mọi cách đặt thau thì mỗi thau nước chỉ có thể hứng tối đa một điểm chảy nước, do đó ~2~ thau nước không thể hứng cả ~3~ điểm chảy nước.
Ở ví dụ thứ tư, ta có thể đặt hai thau nước lần lượt ở vị trí ~[0, 5]~ và ~[1, 6]~ (phần giao của hai thau nước có thể có chiều dài lớn hơn ~0~)
Điểm: 1000
Henya là một thiên tài. Tất cả mọi người đều yêu quý Henya, không chỉ vì cô có IQ lên đến ~999~, mà còn vì cô có khả năng tạo ra âm thanh của ấm đun nước bằng giọng của mình rất vui tai.
Với trí thông minh của mình, Henya có nhiều ý tưởng kì quái nhưng cũng rất thú vị. Vào một ngày buồn không có việc gì làm, Henya đã phát minh ra một dàn nhạc chỉ với những ấm đun nước! Henya có ~n~ ấm đun nước, với một số ấm nước hiện tại đang bật, và một số ấm đang tắt. Henya nói rằng khi tất cả các ấm nước được bật, chúng sẽ sôi cùng một lúc và lúc đó một bản hòa ca tuyệt vời sẽ được chơi.
Là một fan của Henya, bạn rất muốn được nghe bản hòa ca này. Do đó Henya đố bạn bật được hết các ấm nước lên mà chỉ được pháp thực hiện các thao tác sau (không, một, hoặc nhiều lần):
- Chọn ra ít nhất ~a~ và nhiều nhất ~b~ ấm nước tùy ý và đổi trạng thái các ấm nước này (bật thành tắt hoặc ngược lại).
Hãy kiểm tra xem liệu bạn có thể bật được hết các ấm nước hay không chỉ với thao tác mà Heyna đã đề ra.
Input
Dòng đầu tiên gồm số nguyên dương ~t~ (~1 \leq t \leq 100~) — số lượng các test case. Mô tả của mỗi test case như sau.
Dòng đầu tiên gồm ba số nguyên dương ~n~, ~a~, ~b~ (~1 \leq a \leq b \leq n \leq 100~) — số lượng ấm nước của Henya và số lượng ấm nước ít nhất và nhiều nhất mà bạn có thể đổi trạng thái ở mỗi thao tác.
Dòng thứ hai gồm một xâu nhị phân ~s~ độ dài ~n~.
~s_i = 0~ thể hiện ấm nước thứ ~i~ lúc đầu đang tắt,
ngược lại ~s_i = 1~ thể hiện ấn nước thứ ~i~ lúc đầu đang bật.
Output
Với mỗi test case, in ra "YES" (không chứa ngoặc nháy) nếu bạn có thể bật tất cả các ấm nước và thưởng thức bản hòa ca. Ngược lại hãy in ra "NO" (không chứa ngoặc nháy).
Scoring
Số điểm nhận được nếu bạn giải thành công bài toán này là ~1000~ điểm.
Sample Input 1
3
7 3 4
0000000
3 3 3
101
3 2 3
101
Sample Output 1
YES
NO
YES
Notes
Ở ví dụ đầu tiên, bạn có thể bật ~3~ ấm nước đầu tiên, sau đó bật ~4~ ấm nước cuối cùng.
Ở ví dụ thứ hai, bạn chỉ có thể chọn cả ~3~ ấm nước và đổi trạng thái của chúng. Khi đổi trạng thấy lần đầu tiên bạn sẽ thu được trạng thái các ấm nước là 010. Sau lần thứ hai sẽ thu được trạng thái 101 – đây chính là trạng thái ban đầu. Do đó không có cách nào để bật hết các ấm nước.
Ở ví dụ thứ ba, được phép chọn ít nhất ~2~ ấm nước để thay đổi trạng thái. Bạn có thể thực hiện các thao tác sau, với ấm nước được chọn là các ấm nước được gạch chân:
$$\underline{\texttt{1}}\texttt{0}\underline{\texttt{1}} \rightarrow \underline{\texttt{0}\texttt{0}\texttt{0}} \rightarrow \texttt{111}$$
Điểm: 1750
Trong chuyến đi công tác của mình đến một hòn đảo, nhà nghiên cứu FireGhost đã phát hiện ra một bộ tộc kì lạ ở đây. Bộ tộc này có ~n~ người, mỗi người trong bộ tộc có thể là một người trung thực — luôn nói thật, hoặc có thể là một kẻ giả dối — luôn nói dối.
Để điều tra kĩ hơn về bộ tộc này, FireGhost xếp ~n~ người thành một hàng ngang, sau đó đặt câu hỏi cho từng người:
- "Số người trung thực ở bên trái của bạn có nhiều hơn hoặc bằng bên phải hay không?"
Mỗi người chỉ được phép trả lời "có" hoặc "không". Với tính cách của mình, một người trung thực sẽ luôn nói đúng sự thật; ngược lại, một kẻ giả dối sẽ luôn nói sai sự thật.
Sau đó, FireGhost ghi kết quả trả lời câu hỏi vào một tờ giấy. Tuy nhiên, vì sơ suất nên anh ấy đã quên ghi lại tính cách của từng người: ai là người trung thực, và ai là kẻ giả dối. Dựa vào kết quả trả lời câu hỏi, hãy giúp FireGhost tìm ra tính cách của từng người nhé!
Input
Mỗi input sẽ gồm nhiều test cases. Dòng đầu tiên của input gồm số nguyên dương ~t~ (~1 \le t \le 10^4~) — số test cases của bài toán. Sau đây là mô tả của các test cases.
Dòng đầu tiên của mỗi test case gồm số nguyên dương ~n~ (~1 \le n \le 3 \cdot 10^5~) — số người trong bộ tộc.
Dòng thứ hai của mỗi test case gồm ~n~ số nguyên ~p_1, p_2, \ldots, p_n~ (~p_i \in \left \{ 0, 1 \right \}~) — câu trả lời của mỗi người cho câu hỏi. Nếu ~p_i = 1~, đáp án của người thứ ~i~ là "có"; ngược lại, nếu ~p_i = 0~, đáp án của người thứ ~i~ là "không".
Dữ liệu đảm bảo tổng của ~n~ trong tất cả các test cases không vượt quá ~3 \cdot 10^5~.
Output
In ra đáp án cho từng test case:
nếu không thể khôi phục tính cách của từng người, in ra ~-1~.
ngược lại, in ra ~n~ số nguyên ~c_1, c_2, \ldots, c_n~ (~c_i \in \left \{ 0, 1 \right \}~) thể hiện tính cách của từng người:
nếu người thứ ~i~ là một người trung thực (luôn nói thật), ~c_i = 1~.
ngược lại, nếu người thứ ~i~ là một kẻ giả dối (luôn nói dối), ~c_i = 0~.
Nếu có nhiều đáp án thỏa mãn, hãy in ra một đáp án bất kì.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | 500 | ~t \le 100~ và ~n \le 16~ |
| ~2~ | 1250 | không có giới hạn gì thêm |
| Tổng | 1750 |
Sample Input 1
3
5
1 0 0 1 0
1
0
3
1 1 1
Sample Output 1
0 1 0 1 0
0
0 0 1
Notes
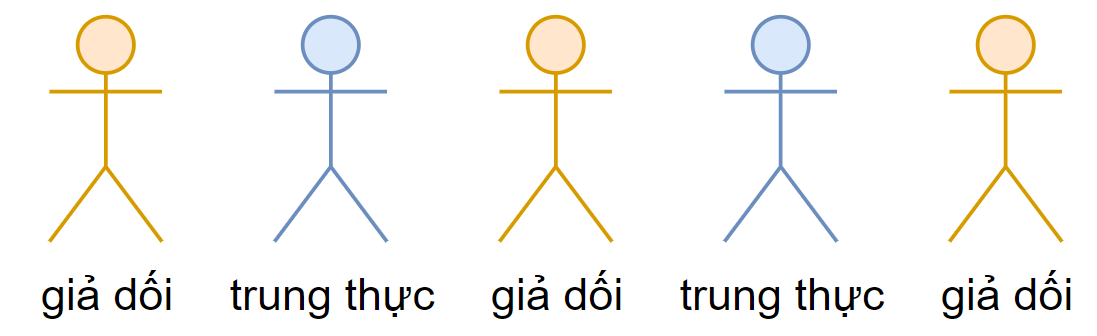
Minh họa cho test case đầu tiên.
Ở test case đầu tiên:
Số người trung thực ở bên trái và bên phải người thứ ~1~ lần lượt là ~0~ và ~2~. Vì người thứ ~1~ là một kẻ giả dối, câu trả lời của anh ta sẽ là "có".
Số người trung thực ở bên trái và bên phải người thứ ~2~ lần lượt là ~0~ và ~1~. Vì người thứ ~2~ là một người trung thực, câu trả lời của anh ta sẽ là "không".
Số người trung thực ở bên trái và bên phải người thứ ~3~ lần lượt là ~1~ và ~1~. Vì người thứ ~3~ là một kẻ giả dối, câu trả lời của anh ta sẽ là "không".
Số người trung thực ở bên trái và bên phải người thứ ~4~ lần lượt là ~1~ và ~0~. Vì người thứ ~4~ là một người trung thực, câu trả lời của anh ta sẽ là "có".
Số người trung thực ở bên trái và bên phải người thứ ~5~ lần lượt là ~2~ và ~0~. Vì người thứ ~5~ là một kẻ giả dối, câu trả lời của anh ta sẽ là "không".
Nhà bé MofK có ~n~ khu vườn, mỗi khu vườn trồng một trong ~k~ loại quả: khu vườn thứ ~i~ trồng loại quả ~t_i~ và có ~a_i~ quả.
Để có nguyên liệu làm bánh, mẹ bé MofK giao cho bé đi hái quả. MofK sẽ chọn một đoạn ~[l..r]~ và hái hết quả ở những khu vườn đó. Mỗi bánh cần nguyên liệu là một quả mỗi loại, vì vậy nếu MofK lần lượt hái được ~x_1, x_2, \ldots, x_k~ quả mỗi loại, mẹ sẽ làm được ~\min(x_1, x_2, \ldots, x_k)~ bánh, số quả còn dư sẽ thưởng cho bé MofK. Nói cách khác, bé MofK sẽ được ăn ~x_1 + x_2 + \ldots + x_k - k \cdot \min(x_1, x_2, \ldots, x_k)~ quả.
Hãy giúp bé MofK chọn đoạn ~[l..r]~ để được ăn nhiều quả nhất nhé!
Input
Dòng đầu tiên chứa hai số nguyên dương ~n~ và ~k~ (~1 \le n, k \le 3 \cdot 10^5~) — số khu vườn và số loại quả được trồng.
Dòng tiếp theo chứa ~n~ số nguyên dương ~t_1, t_2, \ldots, t_n~ (~1 \le t_i \le k~) — loại quả được trồng trong khu vườn thứ ~i~.
Dòng cuối cùng chứa ~n~ số nguyên dương ~a_1, a_2, \ldots, a_n~ (~1 \le a_i \le 10^9~) — số lượng quả được trồng trong khu vườn thứ ~i~.
Output
In ra một số nguyên dương duy nhất: số lượng quả lớn nhất mà bé MofK có thể được ăn.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | 500 | ~n, k \le 500~ |
| ~2~ | 500 | ~n, k \le 2000~ |
| ~3~ | 1250 | không có giới hạn gì thêm |
| Tổng | 2250 |
Sample Input 1
4 3
2 1 2 3
6 3 3 4
Sample Output 1
12
Sample Input 2
4 1
1 1 1 1
3 2 6 2
Sample Output 2
0
Notes
Ở test mẫu đầu tiên, ta có thể chọn đoạn ~[1, 3]~; khi đó, số lượng quả MofK hái được lần lượt là ~[3, 9, 0]~, vì vậy số lượng quả còn lại bé MofK được ăn là ~3 + 9 + 0 - 3 \cdot 0 = 12~.
Ở test mẫu thứ hai, vì chỉ có một loại quả duy nhất nên toàn bộ số quả mà MofK hái được sẽ đem đi làm bánh, và MofK sẽ không có quả nào để ăn. :(
Đây là một bài toán tương tác.
Alice và Bob đang chơi một trò chơi. Có ~n~ lỗ trống trên một hàng ngang, các lỗ được đánh số từ ~1~ đến ~n~ từ trái qua phải. Ban đầu, mỗi lỗ trong ~k~ lỗ cuối cùng có một viên bi ở trong. Alice là người chơi trước và hai người sẽ thay phiên nhau thực hiện các nước đi như sau:
Chọn một viên bi mà bên trái nó có ít nhất một lỗ trống.
Di chuyển viên bi này đến một ô trống bất kì ở bên trái. Lưu ý rằng bạn có thể di chuyển viên bi vượt qua các viên bi khác.
Người đầu tiên chuyển các viên bi đến ~k~ lỗ đầu tiên sẽ chiến thắng. Biết rằng cả hai người đều chơi tối ưu, bạn cần đóng vai một trong hai người và dành chiến thắng.
Input
Dòng đầu tiên gồm một số nguyên ~t~ (~1 \le t \le 50~) — số test case. Sau đây là mô tả các test case.
Mỗi dòng trong ~t~ dòng gồm hai số nguyên ~n~ và ~k~ (~1 \le k < n \le 1000~, ~1 \le k \le 50~) — số lỗ trống và số viên bi cho mỗi test case.
Bạn cần bắt đầu quá trình tương tác cho mỗi test case sau khi đọc ~n~ và ~k~.
Dữ liệu đảm bảo tổng ~n~ qua các bộ dữ liệu không vượt qua ~1000~.
Interaction
Để bắt đầu tương tác, in ra Alice hoặc Bob trên một dòng tương ứng với người mà bạn muốn đóng vai.
Xét nước đi di chuyển viên bi từ lỗ ~x~ sang lỗ ~y~, nước đi này được coi là không hợp lệ nếu một trong các điều sau xảy ra:
- ~x > n~ hoặc ~x \le y~ hoặc ~y \le 0~.
- Lỗ ~x~ trống.
- Lỗ ~y~ đang có bi.
Khi đến lượt của bạn, in ra nước đi của bạn dưới dạng "move ~x\ y~".
Khi đến lượt của máy chấm, đọc vào nước đi của máy chấm dưới dạng "~cmd\ x\ y~".
- ~cmd=~ move: Máy chấm thực hiện nước đi ~(x, y)~.
- ~cmd=~ end: Trò chơi kết thúc.
- ~x=y=-1~: Máy chấm không thể thực hiện nước đi hợp lệ và bạn thắng. Trong trường hợp này chương trình của bạn cần chuyển sang bộ dữ liệu tiếp theo hoặc dừng ngay lập tức khi đã xử lý hết các bộ dữ liệu.
- Ngược lại: Máy chấm thực hiện nước đi cuối cùng ~(x, y)~ và chiến thắng. Trong trường hợp này chương trình của bạn cần dừng ngay lập tức.
- Nếu ~cmd=~ invalid: Ở lượt trước đó, bạn đã thực hiện một nước đi không hợp lệ. Lúc này bạn cần dừng chương trình ngay lập tức.
Sau khi in ra người chơi bạn đóng vai hoặc một nước đi, đừng quên xuống dòng và flush đầu ra chuẩn, nếu không bạn có thể nhận verdict Time limit exceeded. Để làm điều này, bạn có thể sử dụng:
- fflush(stdout) hoặc cout.flush() trong C++;
- System.out.flush() trong Java;
- fflush(output) trong Pascal;
- stdout.flush() trong Python;
- xem tài liệu chuẩn đối với các ngôn ngữ khác.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | 750 | ~k\le 2~ |
| 2 | 750 | ~n\le 20~ |
| 3 | 1250 | Không có ràng buộc gì thêm |
| Tổng | 2750 |
Sample interaction
| Đầu vào chuẩn | Đầu ra chuẩn | Chú thích | Trạng thái các viên bi |
|---|---|---|---|
1 |
Số lượng test case là ~1~ | ||
5 2 |
Test case đầu tiên, ~n = 5~, ~k = 2~ | _ _ _ * * |
|
Alice |
Thí sinh chọn vai trò của Alice và đi trước |
_ _ _ * * |
|
move 5 3 |
Thí sinh di chuyển viên bi từ vị trí ~5~ đến ~3~ | _ _ * * _ |
|
move 3 2 |
BTC di chuyển viên bi từ vị trí ~3~ đến ~2~ | _ * _ * _ |
|
move 4 1 |
Thí sinh di chuyển viên bi từ vị trí ~4~ đến ~1~ | * * _ _ _ |
|
end -1 -1 |
BTC chấp nhận thua cuộc. | * * _ _ _ |
Kuroni rất thích xài tính năng tìm xâu bằng Ctrl-F khi lập trình, đặc biệt là Kuroni cực kì mê mẩn tính năng highlight những đoạn giống với xâu cần tìm. Mỗi khi được cho hai xâu cùng độ dài ~s~ và ~t~, Kuroni sẽ tìm cho bằng được cách để tạo ra hình ảnh highlight giống nhau trên hai xâu này.
Nói cách khác, Kuroni muốn tìm các cặp xâu ~u~ và ~v~ sao cho:
Độ dài của ~u~ bằng độ dài của ~v~.
Xâu ~u~ phải là xâu con của ~s~; đồng thời, xâu ~v~ phải là xâu con của ~t~.
Xâu ~u~ là xâu con bắt đầu từ vị trí ~i~ trên ~s~ khi và chỉ khi xâu ~v~ là xâu con bắt đầu từ vị trí ~i~ trên ~t~ (với mọi ~1 \le i \le |s| - |u| + 1~).
Hãy tìm số lượng cặp xâu ~(u, v)~ thỏa mãn điều kiện trên; cùng với đó, hãy in ra tổng độ dài của ~u~ ở mọi cặp xâu như thế.
Input
Dòng đầu tiên của input gồm số nguyên dương ~n~ (~1 \le n \le 2 \cdot 10^5~) — độ dài của xâu ~s~ và ~t~.
Dòng thứ hai và dòng thứ ba của input lần lượt là xâu ~s~ và xâu ~t~ (~|s| = |t| = n~). ~s~ và ~t~ chỉ bao gồm các kí tự Latin in thường.
Output
In ra hai số nguyên tách nhau bởi dấu cách là số lượng cặp xâu ~(u, v)~ thỏa mãn điều kiện của đề bài và tổng độ dài của ~u~ ở mọi cặp xâu như thế.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | 750 | ~n \le 200~ |
| 2 | 1000 | ~n \le 2000~ |
| 3 | 1250 | không có giới hạn gì thêm |
| Tổng | 3000 |
Sample Input 1
6
banana
kokoro
Sample Output 1
9 35
Sample Input 2
6
tuturu
kokoro
Sample Output 2
17 51
Sample Input 3
10
abcabxabcd
tyztyotyok
Sample Output 3
40 194
Notes
Ở test ví dụ đầu tiên, ~u = \texttt{a}~ và ~v = \texttt{o}~ là một cặp xâu thỏa mãn, trong khi ~u = \texttt{ana}~ và ~v = \texttt{kok}~ không phải là một cặp xâu thỏa mãn.
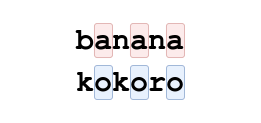
Highlight của Ctrl-F ở test ví dụ đầu tiên với ~u = \texttt{a}~ và ~v = \texttt{o}~.
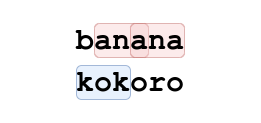
Highlight của Ctrl-F ở test ví dụ đầu tiên với ~u = \texttt{ana}~ và ~v = \texttt{kok}~.
Điểm: 3500
Đối với một lập trình viên, ngoài kiến thức và kĩ năng chuyên môn thì việc rèn luyện thể dục thể thao thường xuyên để giữ thân thể khỏe mạnh là điều rất quan trọng. Hiểu được điều đó, VNOI đã tổ chức cuộc thi chạy "Coder me run" nhằm khuyến khích phong trào luyện tập thể dục thể thao của bạn lập trình viên trên cả nước.
Cuộc thi sẽ được tổ chức tại ~n~ địa điểm. Các địa điểm này được nối với nhau bằng ~m~ đoạn đường hai chiều, đoạn đường thứ ~i~ nối giữa hai địa điểm ~u_i~ và ~v_i~. Giữa hai địa điểm bất kì luôn có thể đi đến được với nhau thông qua một hoặc một số đoạn đường. Đồng thời giữa hai địa điểm bất kì không có quá một cạnh nối giữa chúng.
Năm nay, chủ để của đường chạy Coder me run là "Sắc màu". Ban tổ chức (BTC) đã nhuộm nền đoạn đường thứ ~i~ bằng màu ~c_i~. Khi đi qua một đoạn đường bất kì, màu của thí sinh sẽ được nhuộm bằng màu của đoạn đường đó. Khi đến một địa điểm bất kì, màu của địa điểm đó sẽ được nhuộm bằng màu hiện tại của thí sinh. Ban đầu, thí sinh không được nhuộm màu và có thể chọn bất kì địa điểm nào để xuất phát. Để hoàn thành phần thi của mình, thí sinh cần nhuộm màu của địa điểm i ~u~ thành màu ~s_u~.
Là một thành viên trong BTC, bạn được giao nhiệm vụ kiểm tra xem liệu thí sinh có cách nào để hoàn thành phần thi của mình hay không. Cụ thể, bạn cần đưa ra một đường chạy bất kì để tô màu các địa điểm thỏa yêu cầu mà BTC đề ra, hoặc cho biết điều đó là không khả thi.
Input
Dòng đầu tiên gồm ba số nguyên ~n~, ~m~ (~1 \le n \le 20\,000~, ~n-1 \le m \le \min \big(\frac{n(n-1)}{2},20\,000 \big)~) — số địa điểm của cuộc thi và số đoạn đường.
Dòng thứ hai gồm ~n~ số nguyên ~s_1, s_2, \ldots, s_n~ (~1 \le s_i \le n~) — màu mà thí sinh cần nhuộm cho các địa điểm.
~m~ dòng tiếp theo, dòng thứ ~i~ gồm ba số nguyên ~u_i~, ~v_i~, ~c_i~ (~1 \le u_i, v_i, c_v \le n~, ~u_i \ne v_i~) — mô tả hai địa điểm được nối bởi đoạn đường thứ ~i~ và màu được nhuộm cho đoạn đường này.
Dữ liệu vào đảm bảo giữa hai địa điểm bất kì đều có thể đi đến được nhau thông qua một hoặc một số đoạn đường. Đồng thời giữa hai địa điểm bất kì không có quá một cạnh nối giữa chúng.
Output
Ở dòng đầu tiên, in ra "YES" (không chứa ngoặc nháy) nếu tồn tại một đường chạy để nhuộm màu các địa điểm thỏa yêu cầu của BTC; nếu không, in ra "NO" (không chứa ngoặc nháy).
Nếu dòng đầu tiên in ra "YES", bạn cần in ra ở dòng thứ hai số ~k~ không quá ~10^5~ là số địa điểm của đường chạy tìm được. Ta có thể chứng minh được rằng dưới giới hạn của bài này, nếu tồn tại một đường chạy thỏa mãn điều kiện thì cũng tồn tại một đường chạy không đi qua quá ~10^5~ địa điểm.
Tiếp theo, bạn cần in ra ở dòng thứ ba ~k~ số nguyên ~p_1, p_2, \ldots, p_k~ (~1 \le p_i \le n~ với mọi ~1 \le i \le k~) cho biết thứ tự các địa điểm được đi qua trong đường chạy.
Lưu ý rằng, bạn không cần tìm đường chạy thỏa yêu cầu đề bài đi qua ít địa điểm nhất.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | 1250 | ~n \le 16~ |
| ~2~ | 1500 | ~n \le 200~ |
| ~3~ | 750 | không có giới hạn gì thêm |
| Tổng | 3500 |
Sample Input 1
3 2
1 1 2
1 2 1
2 3 2
Sample Output 1
YES
4
2 1 2 3
Sample Input 2
4 4
1 1 2 3
1 2 1
2 3 2
1 4 1
3 4 1
Sample Output 2
NO
Sample Input 3
5 7
1 2 2 1 3
1 2 1
1 3 3
2 4 2
5 1 1
5 2 3
5 3 2
5 4 1
Sample Output 3
YES
7
2 1 5 4 2 5 3
Notes
Ở ví dụ đầu tiên, ta có hình minh họa cho đường chạy thỏa yêu cầu đề bài bên dưới. Hai màu ~1~ và ~2~ được biểu diễn bằng màu đỏ và màu xanh lá cây.
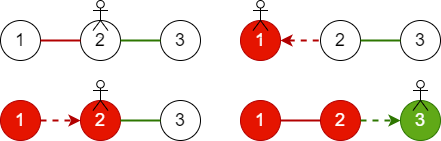
Hình vẽ minh họa ví dụ thứ nhất.
Ở ví dụ thứ hai, do các đoạn đường chỉ được nhuộm màu ~1~ và ~2~ nên không thể nhuộm màu địa điểm ~4~ thành màu ~3~.
Ở ví dụ thứ ba, tương tự, ta có hình minh họa đường chạy bên dưới. Màu ~3~ được biểu diễn bằng màu xanh dương.
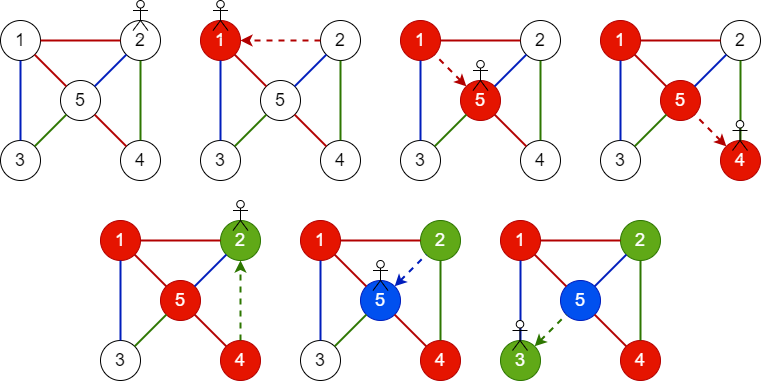
Hình vẽ minh họa ví dụ thứ hai.