Coder me run
Xem dạng PDFĐối với một lập trình viên, ngoài kiến thức và kĩ năng chuyên môn thì việc rèn luyện thể dục thể thao thường xuyên để giữ thân thể khỏe mạnh là điều rất quan trọng. Hiểu được điều đó, VNOI đã tổ chức cuộc thi chạy "Coder me run" nhằm khuyến khích phong trào luyện tập thể dục thể thao của bạn lập trình viên trên cả nước.
Cuộc thi sẽ được tổ chức tại ~n~ địa điểm. Các địa điểm này được nối với nhau bằng ~m~ đoạn đường hai chiều, đoạn đường thứ ~i~ nối giữa hai địa điểm ~u_i~ và ~v_i~. Giữa hai địa điểm bất kì luôn có thể đi đến được với nhau thông qua một hoặc một số đoạn đường. Đồng thời giữa hai địa điểm bất kì không có quá một cạnh nối giữa chúng.
Năm nay, chủ để của đường chạy Coder me run là "Sắc màu". Ban tổ chức (BTC) đã nhuộm nền đoạn đường thứ ~i~ bằng màu ~c_i~. Khi đi qua một đoạn đường bất kì, màu của thí sinh sẽ được nhuộm bằng màu của đoạn đường đó. Khi đến một địa điểm bất kì, màu của địa điểm đó sẽ được nhuộm bằng màu hiện tại của thí sinh. Ban đầu, thí sinh không được nhuộm màu và có thể chọn bất kì địa điểm nào để xuất phát. Để hoàn thành phần thi của mình, thí sinh cần nhuộm màu của địa điểm i ~u~ thành màu ~s_u~.
Là một thành viên trong BTC, bạn được giao nhiệm vụ kiểm tra xem liệu thí sinh có cách nào để hoàn thành phần thi của mình hay không. Cụ thể, bạn cần đưa ra một đường chạy bất kì để tô màu các địa điểm thỏa yêu cầu mà BTC đề ra, hoặc cho biết điều đó là không khả thi.
Input
Dòng đầu tiên gồm ba số nguyên ~n~, ~m~ (~1 \le n \le 20\,000~, ~n-1 \le m \le \min \big(\frac{n(n-1)}{2},20\,000 \big)~) — số địa điểm của cuộc thi và số đoạn đường.
Dòng thứ hai gồm ~n~ số nguyên ~s_1, s_2, \ldots, s_n~ (~1 \le s_i \le n~) — màu mà thí sinh cần nhuộm cho các địa điểm.
~m~ dòng tiếp theo, dòng thứ ~i~ gồm ba số nguyên ~u_i~, ~v_i~, ~c_i~ (~1 \le u_i, v_i, c_v \le n~, ~u_i \ne v_i~) — mô tả hai địa điểm được nối bởi đoạn đường thứ ~i~ và màu được nhuộm cho đoạn đường này.
Dữ liệu vào đảm bảo giữa hai địa điểm bất kì đều có thể đi đến được nhau thông qua một hoặc một số đoạn đường. Đồng thời giữa hai địa điểm bất kì không có quá một cạnh nối giữa chúng.
Output
Ở dòng đầu tiên, in ra "YES" (không chứa ngoặc nháy) nếu tồn tại một đường chạy để nhuộm màu các địa điểm thỏa yêu cầu của BTC; nếu không, in ra "NO" (không chứa ngoặc nháy).
Nếu dòng đầu tiên in ra "YES", bạn cần in ra ở dòng thứ hai số ~k~ không quá ~10^5~ là số địa điểm của đường chạy tìm được. Ta có thể chứng minh được rằng dưới giới hạn của bài này, nếu tồn tại một đường chạy thỏa mãn điều kiện thì cũng tồn tại một đường chạy không đi qua quá ~10^5~ địa điểm.
Tiếp theo, bạn cần in ra ở dòng thứ ba ~k~ số nguyên ~p_1, p_2, \ldots, p_k~ (~1 \le p_i \le n~ với mọi ~1 \le i \le k~) cho biết thứ tự các địa điểm được đi qua trong đường chạy.
Lưu ý rằng, bạn không cần tìm đường chạy thỏa yêu cầu đề bài đi qua ít địa điểm nhất.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | 1250 | ~n \le 16~ |
| ~2~ | 1500 | ~n \le 200~ |
| ~3~ | 750 | không có giới hạn gì thêm |
| Tổng | 3500 |
Sample Input 1
3 2
1 1 2
1 2 1
2 3 2
Sample Output 1
YES
4
2 1 2 3
Sample Input 2
4 4
1 1 2 3
1 2 1
2 3 2
1 4 1
3 4 1
Sample Output 2
NO
Sample Input 3
5 7
1 2 2 1 3
1 2 1
1 3 3
2 4 2
5 1 1
5 2 3
5 3 2
5 4 1
Sample Output 3
YES
7
2 1 5 4 2 5 3
Notes
Ở ví dụ đầu tiên, ta có hình minh họa cho đường chạy thỏa yêu cầu đề bài bên dưới. Hai màu ~1~ và ~2~ được biểu diễn bằng màu đỏ và màu xanh lá cây.
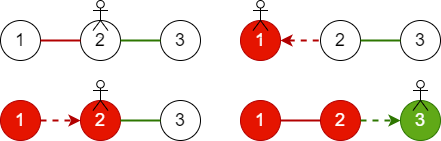
Hình vẽ minh họa ví dụ thứ nhất.
Ở ví dụ thứ hai, do các đoạn đường chỉ được nhuộm màu ~1~ và ~2~ nên không thể nhuộm màu địa điểm ~4~ thành màu ~3~.
Ở ví dụ thứ ba, tương tự, ta có hình minh họa đường chạy bên dưới. Màu ~3~ được biểu diễn bằng màu xanh dương.
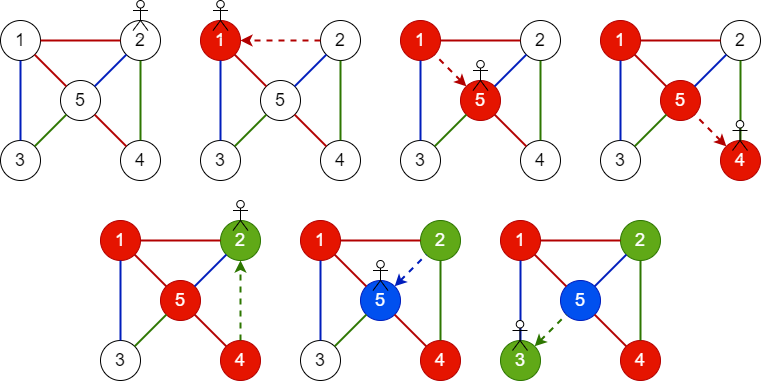
Hình vẽ minh họa ví dụ thứ hai.
Bình luận