Tin chuẩn chưa anh
Xem dạng PDFTrong chuyến đi công tác của mình đến một hòn đảo, nhà nghiên cứu FireGhost đã phát hiện ra một bộ tộc kì lạ ở đây. Bộ tộc này có ~n~ người, mỗi người trong bộ tộc có thể là một người trung thực — luôn nói thật, hoặc có thể là một kẻ giả dối — luôn nói dối.
Để điều tra kĩ hơn về bộ tộc này, FireGhost xếp ~n~ người thành một hàng ngang, sau đó đặt câu hỏi cho từng người:
- "Số người trung thực ở bên trái của bạn có nhiều hơn hoặc bằng bên phải hay không?"
Mỗi người chỉ được phép trả lời "có" hoặc "không". Với tính cách của mình, một người trung thực sẽ luôn nói đúng sự thật; ngược lại, một kẻ giả dối sẽ luôn nói sai sự thật.
Sau đó, FireGhost ghi kết quả trả lời câu hỏi vào một tờ giấy. Tuy nhiên, vì sơ suất nên anh ấy đã quên ghi lại tính cách của từng người: ai là người trung thực, và ai là kẻ giả dối. Dựa vào kết quả trả lời câu hỏi, hãy giúp FireGhost tìm ra tính cách của từng người nhé!
Input
Mỗi input sẽ gồm nhiều test cases. Dòng đầu tiên của input gồm số nguyên dương ~t~ (~1 \le t \le 10^4~) — số test cases của bài toán. Sau đây là mô tả của các test cases.
Dòng đầu tiên của mỗi test case gồm số nguyên dương ~n~ (~1 \le n \le 3 \cdot 10^5~) — số người trong bộ tộc.
Dòng thứ hai của mỗi test case gồm ~n~ số nguyên ~p_1, p_2, \ldots, p_n~ (~p_i \in \left \{ 0, 1 \right \}~) — câu trả lời của mỗi người cho câu hỏi. Nếu ~p_i = 1~, đáp án của người thứ ~i~ là "có"; ngược lại, nếu ~p_i = 0~, đáp án của người thứ ~i~ là "không".
Dữ liệu đảm bảo tổng của ~n~ trong tất cả các test cases không vượt quá ~3 \cdot 10^5~.
Output
In ra đáp án cho từng test case:
nếu không thể khôi phục tính cách của từng người, in ra ~-1~.
ngược lại, in ra ~n~ số nguyên ~c_1, c_2, \ldots, c_n~ (~c_i \in \left \{ 0, 1 \right \}~) thể hiện tính cách của từng người:
nếu người thứ ~i~ là một người trung thực (luôn nói thật), ~c_i = 1~.
ngược lại, nếu người thứ ~i~ là một kẻ giả dối (luôn nói dối), ~c_i = 0~.
Nếu có nhiều đáp án thỏa mãn, hãy in ra một đáp án bất kì.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | 500 | ~t \le 100~ và ~n \le 16~ |
| ~2~ | 1250 | không có giới hạn gì thêm |
| Tổng | 1750 |
Sample Input 1
3
5
1 0 0 1 0
1
0
3
1 1 1
Sample Output 1
0 1 0 1 0
0
0 0 1
Notes
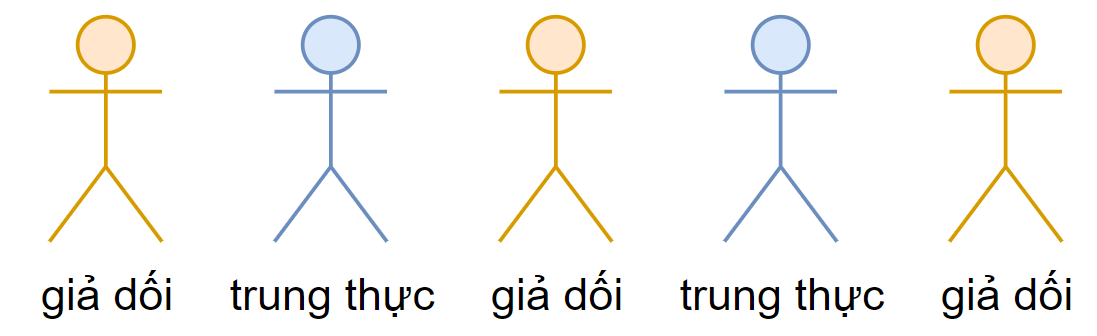
Minh họa cho test case đầu tiên.
Ở test case đầu tiên:
Số người trung thực ở bên trái và bên phải người thứ ~1~ lần lượt là ~0~ và ~2~. Vì người thứ ~1~ là một kẻ giả dối, câu trả lời của anh ta sẽ là "có".
Số người trung thực ở bên trái và bên phải người thứ ~2~ lần lượt là ~0~ và ~1~. Vì người thứ ~2~ là một người trung thực, câu trả lời của anh ta sẽ là "không".
Số người trung thực ở bên trái và bên phải người thứ ~3~ lần lượt là ~1~ và ~1~. Vì người thứ ~3~ là một kẻ giả dối, câu trả lời của anh ta sẽ là "không".
Số người trung thực ở bên trái và bên phải người thứ ~4~ lần lượt là ~1~ và ~0~. Vì người thứ ~4~ là một người trung thực, câu trả lời của anh ta sẽ là "có".
Số người trung thực ở bên trái và bên phải người thứ ~5~ lần lượt là ~2~ và ~0~. Vì người thứ ~5~ là một kẻ giả dối, câu trả lời của anh ta sẽ là "không".
Bình luận