DYTECHLAB ALGORITHMS BATTLE 2022
Điểm: 1

|
Mabư Béo chào các bạn, các bạn đã sẵn sàng cùng Mabư Béo khám phá những điều thú vị đang chờ đón các bạn trên chuyến phiêu lưu này chưa? |
Cho ~N~ que diêm. Que diêm thứ ~i~ có độ dài là ~l_i~.
Mabư Béo dùng một số que diêm để ghép thành đa giác lồi. Hỏi, đa giác lồi với chu vi lớn nhất hắn ta có thể tạo được có chu vi là bao nhiêu?
Trong trường hợp Mabư Béo không thể tạo thành một đa giác lồi nào từ các que diêm đã cho, in ra ~0~.
Input
Dòng đầu tiên chứa ~T~ (~1 \le T \le 100~) - số test trong một tệp đầu vào. Mỗi test sẽ có định dạng như sau:
Dòng thứ nhất chứa ~N~ (~3 \le N \le 100~) - số que diêm mà Majin Buu có.
Dòng thứ hai chứa ~N~ số: ~l_1, l_2, \ldots, l_N~ (~1 \le l_i \le 10^6~) - độ dài các que diêm.
Output
Với mỗi bộ test, nếu không thể tạo thành một đa giác lồi nào từ các que diêm đã cho, in ra ~0~. Ngược lại, in ra chu vi của đa giác lớn nhất Mabư Béo có thể tạo được.
Sample Input 1
4
6
9 3 4 5 50 6
3
1 2 4
7
13 8 5 3 2 1 1
10
1 2 4 8 16 32 64 128 256 512
Sample Output 1
27
0
33
0
Notes
Ở ví dụ đầu tiên, có thể xếp các que diêm có chỉ số lần lượt là: ~1, 2, 3, 4, 6~ thành đa giác như sau:
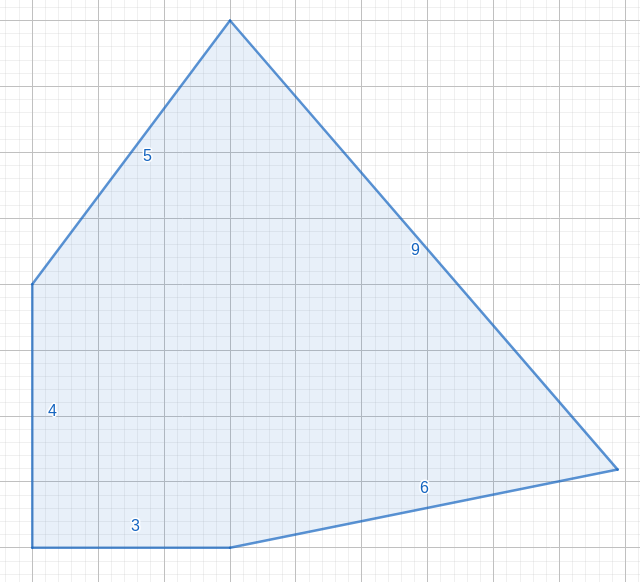
Điểm: 1

|
Mabư Béo, gặp lại hai bậc sư phụ: Goku và Piccolo. Họ cùng với những võ sĩ quyền năng khác ngồi cùng nhau thành một vòng tròn. Mabư Béo phát cho mọi người trong vòng tròn chút bánh quy, và hắn ta đặt ra cho mọi người bài toán: |
Vòng tròn có ~N~ võ sĩ, đánh số từ ~0~ đến ~N - 1~. Võ sĩ thứ ~i~ sở hữu ~A_i~ miếng bánh quy. Với mọi ~i~ từ ~1~ đến ~N - 1~, võ sĩ thứ ~i~ sẽ ngồi bên tay phải võ sĩ thứ ~i - 1~. Võ sĩ được đánh số ~0~ sẽ ngồi bên tay phải võ sĩ được đánh số ~N - 1~. Mabư Béo ngồi ở vị trí được đánh số ~0~ trong vòng tròn.
Mỗi lượt chơi, ngoại trừ lượt đầu tiên, võ sĩ vừa nhận được bánh quy của lượt trước đó sẽ đưa đúng ~\lceil \frac{j + 1}{2} \rceil~ miếng bánh quy cho võ sĩ ngồi bên phải mình. Trong đó, ~j~ thể hiện số lượt chơi đã diễn ra trước lượt chơi hiện tại. Trong trường hợp lượt chơi đầu tiên, Mabư Béo sẽ là người thực hiện. Hắn ta sẽ đưa ~\lceil \frac{0 + 1}{2} \rceil = 1~ miếng bánh quy cho võ sĩ ngồi bên phải mình.
Trò chơi kết thúc khi một võ sĩ không thể thực hiện lượt chơi khi đến lượt mình (không đủ bánh quy để thực hiện lượt chơi). Nói cách khác, trò chơi kết thúc ở lượt chơi mà số bánh mà lượt chơi đó yêu cầu lớn hơn số bánh người chơi lượt đó sở hữu. Khi đó, người chơi không thể thực hiện lượt chơi của mình sẽ bị coi là thua cuộc.
Hãy in ra chỉ số của võ sĩ sẽ thua cuộc trong trò chơi này.
Với một số thực ~x~ bất kỳ, ~\lceil x \rceil~ là số nguyên nhỏ nhất thỏa mãn lớn hơn hoặc bằng ~x~. Ví dụ: ~\lceil 5.3 \rceil = 6~, ~\lceil \sqrt{3} \rceil = 2~, ~\lceil 4.0 \rceil = 4~.
Input
Mỗi file test sẽ chứa nhiều trường hợp test. Dòng đầu tiên chứa số trường hợp test ~T~ (~1 \le T \le 1000~). Mô tả một trường hợp test như sau:
Dòng đầu chứa số nguyên ~N~ (~3 \le N \le 10^5~) - số võ sĩ trong vòng tròn.
Dòng thứ hai chứa ~N~ số nguyên ~A_0, A_1, \ldots, A_{N - 1}~ (~1 \le A_i \le 10^9~) - số bánh quy mỗi võ sĩ có khi bắt đầu trò chơi.
Dữ liệu đảm bảo rằng tổng của ~N~ qua tất cả trường hợp test sẽ không vượt quá ~10^5~.
Output
Với mỗi trường hợp test, in ra một số nguyên duy nhất trên một dòng, thể hiện chỉ số của võ sĩ sẽ thua cuộc trong trò chơi này.
Sample Input 1
5
3
3 2 2
4
3 1 4 2
7
5 4 3 2 3 2 2
10
10 9 8 7 6 5 4 3 2 1
11
11 10 9 8 7 6 5 4 3 2 1
Sample Output 1
2
0
6
8
10
Notes
Mô tả những lượt chơi đầu ở trường hợp test đầu tiên:
Số bánh các võ sĩ sở hữu ban đầu: ~3~, ~2~, ~2~.
Lượt đầu, Mabư Béo (có chỉ số ~0~) sẽ đưa ~\lceil \frac{0 + 1}{2} \rceil = 1~ bánh quy cho võ sĩ ngồi bên phải mình.
Số bánh các võ sĩ sở hữu hiện tại: ~2~, ~3~, ~2~.
Lượt thứ hai, võ sĩ có chỉ số ~1~ sẽ đưa ~\lceil \frac{1 + 1}{2} \rceil = 1~ bánh quy cho võ sĩ ngồi bên phải mình.
Số bánh các võ sĩ sở hữu hiện tại: ~2~, ~2~, ~3~.
Lượt thứ ba, võ sĩ có chỉ số ~2~ sẽ đưa ~\lceil \frac{2 + 1}{2} \rceil = 2~ bánh quy cho võ sĩ ngồi bên phải mình.
Số bánh các võ sĩ sở hữu hiện tại: ~4~, ~2~, ~1~.
Lượt thứ tư, võ sĩ có chỉ số ~0~ sẽ đưa ~\lceil \frac{3 + 1}{2} \rceil = 2~ bánh quy cho võ sĩ ngồi bên phải mình.
Số bánh các võ sĩ sở hữu hiện tại: ~2~, ~4~, ~1~.
Lượt thứ năm, võ sĩ có chỉ số ~1~ sẽ đưa ~\lceil \frac{4 + 1}{2} \rceil = 3~ bánh quy cho võ sĩ ngồi bên phải mình.
Số bánh các võ sĩ sở hữu hiện tại: ~2~, ~1~, ~4~.
Điểm: 1

|
Mabư Béo muốn giảm cân. Hắn ta biết rằng chặng đường đó rất khó khăn và cần nỗ lực khổng lồ (như cái bụng của hắn vậy). Dẫu cho chặng đường có dài đến mấy, điểm bắt đầu cũng sẽ từng những nỗ lực nhỏ bé đầu tiên. |
Buổi chạy bộ đầu tiên của Mabư Béo diễn ra trong vòng ~t~ giây. Hắn ta muốn chạy càng xa càng tốt. Ở đầu buổi tập, năng lượng trong người hắn ở mức ~c~, và tốc độ của hắn là ~0~. Ngưỡng năng lượng của Mabư Béo ở mọi thời điểm là ~c~ (nói cách khác, mức năng lượng của hắn sẽ không bao giờ vượt quá con số này). Tốc độ tối đa hắn có thể chạy được là ~s~.
Tại mỗi thời điểm giây thứ ~t_i~, hắn có thể lựa chọn một trong số những hành động sau:
Tác động gia tốc tức thời vào đôi chân: tốc độ của hắn tăng lên ~1~ đơn vị. Nếu tốc độ trước đó của hắn là ~v_i~ (mét/giây), thì từ thời điểm bắt đầu giây thứ ~t_i~ trở đi, tốc độ của hắn ta trở thành ~v_i + 1~ (mét/giây). Hành động này yêu cầu ~l~ năng lượng.
Duy trì tốc độ hiện tại: tốc độ của hắn giữ nguyên. vị. Nếu tốc độ trước đó của hắn là ~v_i~ (mét/giây), thì từ thời điểm bắt đầu giây thứ ~t_i~ trở đi, tốc độ của hắn vẫn là ~v_i~ (mét/giây). Hành động này yêu cầu ~k~ năng lượng.
Thả lỏng đôi chân: tốc độ của hắn giảm đi ~1~ đơn vị. Nếu tốc độ trước đó của hắn là ~v_i~ (mét/giây), thì từ thời điểm bắt đầu giây thứ ~t_i~ trở đi, tốc độ của hắn ta trở thành ~v_i - 1~ (mét/giây). Hành động này hồi phục ~d~ năng lượng.
Tạm dừng buổi tập. Nếu tốc độ trước đó của hắn là ~v_i~ (mét/giây), thì từ thời điểm bắt đầu giây thứ ~t_i~ trở đi, tốc độ của hắn ta trở thành ~0~. Hành động này hồi phục ~d~ năng lượng.
Lưu ý: Nếu tại một thời điểm nào đó, một hành động nào đó mà tốn lượng năng lượng lớn hơn năng lượng hiện có trong người Mabư Béo, hắn ta sẽ không thể thực hiện. Tuy nhiên, nếu một hành động nào đó hồi năng lượng, khiến cho năng lượng của hắn vượt mức ~c~, hắn vẫn có thể thực hiện. Khi đó năng lượng của hắn sẽ trở về ~c~.
Hỏi: sau ~t~ giây, Mabư Béo có thể chạy được tối đa bao nhiêu mét?
Input
Dòng đầu chứa ~2~ số: ~t~ (~1 \le t \le 1000~) - số giây diễn ra bài tập của Mabư Béo, và ~s~ (~1 \le s \le 100~) - tốc độ tối đa mà Mabư Béo có thể chạy được.
Dòng thứ hai chứa ~4~ số nguyên: ~c~, ~k~, ~l~, ~d~ (~1 \le c \le 100~, ~1 \le k < l \le min(10, c)~, ~1 \le d \le 100~) - lần lượt là: năng lượng ban đầu (đồng thời là năng lượng tối đa) mà Mabư Béo có, năng lượng hắn mất đi nếu duy trì tốc độ, năng lượng hắn mất đi nếu tăng tốc, và năng lượng hắn hồi phục khi giảm tốc.
Output
Một dòng duy nhất: quãng đường lớn nhất Mabư Béo di chuyển được, theo đơn vị mét.
Sample Input 1
6 3
8 1 3 2
Sample Output 1
9
Sample Input 2
10 5
22 2 5 2
Sample Output 2
25
Sample Input 3
42 10
13 2 5 16
Sample Output 3
292
Notes
Ở test đầu tiên: ~t = 6~. Lần lượt trong ~6~ giây, Mabư Béo sẽ thực hiện những hành động:
Tăng tốc ~\rightarrow~ Tăng tốc ~\rightarrow~ Giảm tốc ~\rightarrow~ Tăng tốc ~\rightarrow~ Duy trì ~\rightarrow~ Giảm tốc.
Khi đó, năng lượng của hắn từ giây thứ ~0~ đến giây thứ ~6~ lần lượt là: ~8 \rightarrow 5 \rightarrow 2 \rightarrow 4 \rightarrow 1 \rightarrow 0 \rightarrow 2~.
Và vận tốc lần lượt ở mỗi giây: ~0 \rightarrow 1 \rightarrow 2 \rightarrow 1 \rightarrow 2 \rightarrow 2 \rightarrow 1~.
Tổng quãng đường hắn di chuyển được: ~1 + 2 + 1 + 2 + 2 + 1 = 9~.
Chứng minh được rằng không có cách nào để Mabư Béo di chuyển được nhiều hơn.
Điểm: 1

|
Mabư Béo có bài tập trèo cây ngày hôm nay. Nhưng sau những giờ đạp xe từ đầu tuần mà khiến hắn mệt mỏi đến tận bây giờ, hắn ta quyết định trì hoãn. Để rồi cây duy nhất hắn chinh phục được hôm nay là cây kem béo bở hắn đang cầm trên tay lúc này. |
Piccolo thấy vậy buồn lắm, bèn tận dụng quãng thời gian cậu trì hoãn để thách đố một bài toán tô màu cây như sau:
Một cây hoàn mỹ được định nghĩa như sau:
- Tồn tại ít nhất ~1~ cách để tô mỗi nút của cây bằng hai màu: đen hoặc trắng, sao cho mỗi nút có đúng một và chỉ một nút kề nó được tô cùng màu.
Piccolo đưa cho Mabư Béo một cái cây, có gốc là ~1~, và số đỉnh chẵn. Nhiệm vụ của Mabư Béo là biến cây này trở thành cây hoàn mỹ bằng một số thao tác đảo các nút trong cây. Một thao tác được mô tả như sau:
Chọn một nút ~u~ (~u > 1~), Sau đó chọn một nút ~v~ thỏa mãn không phải một trong những hậu duệ của nút ~u~ (Theo định nghĩa, ~u~ cũng là một trong những hậu duệ của ~u~).
Bỏ cạnh nối nút ~u~ với nút cha của ~u~, sau đó thêm cạnh mới nối ~u~ với ~v~.
Hỏi, số thao tác ít nhất để Mabư Béo cần thực hiện để khiến cây đã cho trở thành Cây Hoàn Mỹ?
Input
Mỗi file test chứa nhiều trường hợp test. Dòng đầu của mỗi file chứa số trường hợp test trong file ~T~ (~1 \le T \le 100~). Mỗi trường hợp test được mô tả như sau:
Dòng đầu chứa số nguyên ~N~ (~2 \le N \le 10^5~) - số nút trong cây mà Piccolo đã đưa. ~N~ luôn chẵn.
~N - 1~ dòng sau, dòng thứ ~i~ chứa hai số nguyên ~x_i~, ~y_i~ (~1 \le x_i, y_i \le N~), thể hiện rằng có cạnh nối giữa hai nút ~x_i~ và ~y_i~. Dữ liệu đảm bảo các cạnh đã cho tạo thành một cây hoàn chỉnh.
Tổng của các ~N~ trong tất cả các trường hợp test không vượt ~10^5~.
Output
Với mỗi trường hợp test, in ra một số nguyên duy nhất, thể hiện số thao tác ít nhất cần thực hiện để khiến cây trở nên hoàn mỹ.
Sample Input 1
4
12
7 6
12 10
9 5
8 12
1 12
11 5
1 9
3 7
1 7
2 5
12 4
8
1 3
1 4
3 5
3 6
4 2
4 7
4 8
4
1 2
2 3
3 4
4
1 2
1 3
1 4
Sample Output 1
2
2
0
1
Notes
Ở trường hợp ví dụ đầu tiên, đây là cây ban đầu:
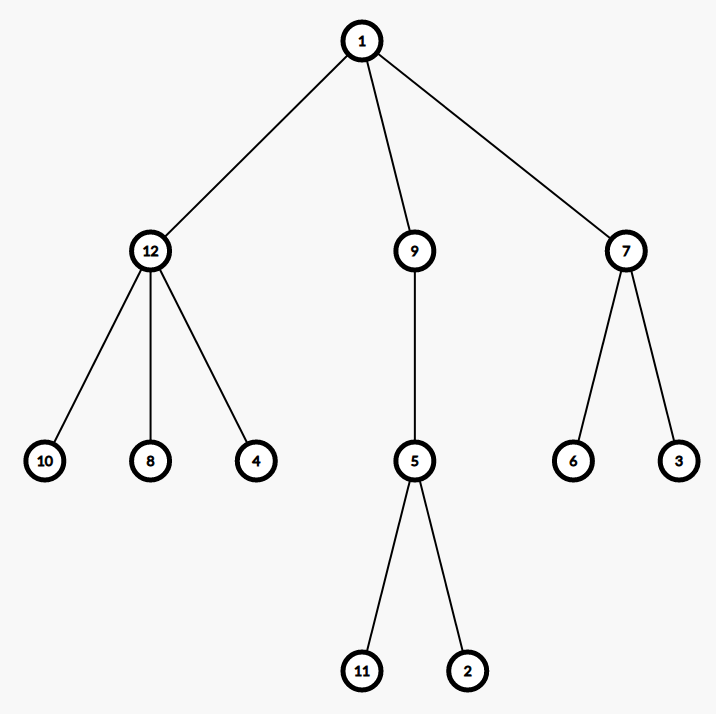
Mabư Béo có thể chọn ngắt kết nối nút ~3~ và ~4~ với cha của chúng, sau đó nối chúng với nút ~8~ với ~2~ lần lượt. Sau đó, tô các nút ~1~, ~2~, ~3~, ~4~, ~8~, ~9~ bằng màu trắng. Các nút còn lại sẽ được tô màu đen.
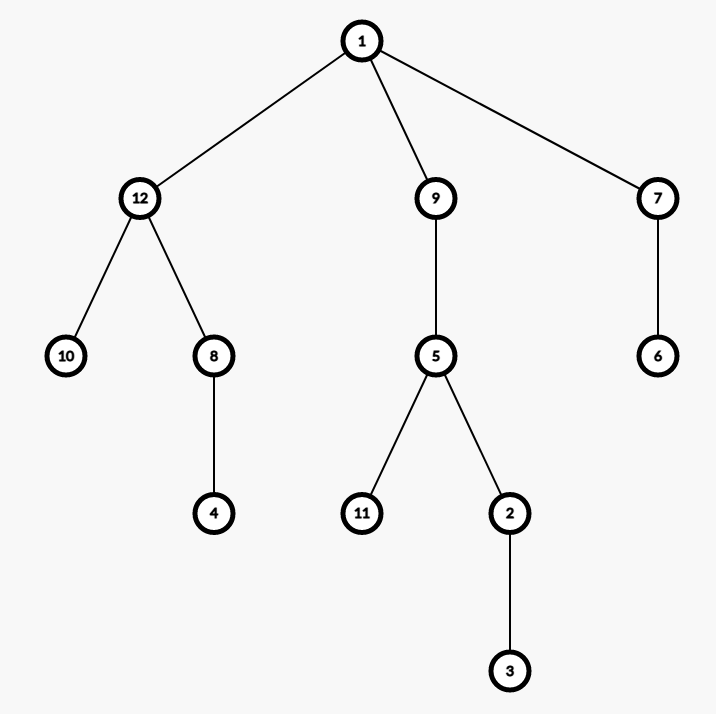
Điểm: 1

|
Mabư Béo đang rất tức giận. Hắn ta có ~M~ giá để tạ đã được phân theo đúng quy tắc. Nhưng ai đó đã vào phòng gym của hắn để xáo tung các quả tạ với nhau, khiến cho hắn ta phải xếp lại chỗ tạ đó. |
Mabư Béo có ~N - 1~ quả tạ, với cân nặng lần lượt là ~1~, ~2~, ~\ldots~, ~N - 1~. ~N~ luôn là số nguyên tố được viết dưới dạng ~3k+1~ với ~k~ nguyên. Hắn cần xếp tạ vào ~M~ giá để tạ, sao cho giá thứ ~i~ có đúng ~a_i~ quả tạ. Mabư Béo muốn tổng cân nặng của các quả tạ trên một giá để tạ phải chia hết cho ~N~.
Hãy chỉ cho hắn một cách xếp tạ lên giá bất kỳ thỏa mãn điều kiện trên.
Input
Dòng đầu tiên chứa ~N~ và ~M~ (~7 \le N \le 99\ 991~, ~N~ là số nguyên tố có dạng ~3k+1~, ~1 \le M \le \lfloor \frac{N}{2} \rfloor~) - thể hiện thông tin về bộ tạ mà Mabư Béo có, và số giá tạ.
Dòng thứ hai chứa ~M~ số nguyên: ~a_1, a_2, \ldots, a_M~ (~2 \le a_i \le N - 1~, tổng các ~a_i~ đúng bằng ~N - 1~) - số quả tạ cần phải xếp lên từng giá tạ.
Output
~M~ dòng, dòng thứ ~i~ chứa đúng ~a_i~ số nguyên, thể hiện ~a_i~ quả tạ bạn muốn xếp lên giá thứ ~i~. Câu trả lời của bạn sẽ được coi là đúng khi:
Tổng cân nặng các quả tạ trên mỗi giá chia hết cho ~N~.
Mỗi quả tạ từ ~1~ đến ~N-1~ xuất hiện duy nhất ~1~ lần giữa tất cả các giá tạ.
Sample Input 1
7 3
2 2 2
Sample Output 1
3 4
2 5
1 6
Sample Input 2
13 4
5 2 3 2
Sample Output 2
5 6 7 9 12
3 10
1 4 8
2 11
Sample Input 3
13 3
3 4 5
Sample Output 3
5 9 12
3 6 7 10
1 2 4 8 11
Sample Input 4
19 3
4 11 3
Sample Output 4
10 9 11 8
14 5 15 4 16 3 17 2 18 13 7
12 6 1
Sample Input 5
7 2
3 3
Sample Output 5
1 2 4
3 5 6
Notes
Lưu ý rằng: mỗi input có thể có rất nhiều đáp án.
Điểm: 1

|
Để ăn mừng kỳ tích giảm cân của hắn, Mabư Béo đã tổ chức... một bữa tiệc bánh quy. |
Có ~N~ chiếc đĩa xếp thành một hàng, được đánh số từ ~1~ đến ~N~ và ~M~ cái bánh quy. Mabư Béo cần phải chia vào mỗi đĩa một số bánh nhất định. Vì hắn ta không biết rằng sẽ có bao nhiêu người đến dự bữa tiệc của mình, nên cách chia của hắn cần phải thỏa mãn được nhiều trường hợp nhất có thể. Cụ thể hơn:
Giả sử có ~K~ khách. Vị khách thứ ~i~ sẽ được sắp xếp để ăn hết bánh có chỉ số từ ~l_i~ đến ~r_i~. Vị khách đó sẽ ăn hết bánh trong khoảng này, và không ăn bánh ở ngoài khoảng này.
Mỗi đĩa bánh đều sẽ có một và chỉ một vị khách được ăn.
Các vị khách đều sẽ phải được ăn số bánh bằng nhau. Từ đó, ta có thể suy ra mỗi vị khách đều sẽ được ăn đúng ~\frac{M}{K}~ chiếc bánh.
Cho trước ~N~ và ~M~. Vì Mabư Béo không biết trước ~K~, hắn muốn cách chia bánh của mình phải thỏa mãn nhiều trường hợp của ~K~ nhất có thể.
Input
Mỗi file test chứa nhiều trường hợp test. Dòng đầu của mỗi file chứa số trường hợp test trong file ~T~ (~1 \le T \le 100~). Mỗi trường hợp test được mô tả như sau:
Một dòng duy nhất chứa hai số nguyên: ~N~ (~1 \le N \le 10^5~) và ~M~ (~N \le M \le 10^{10}~).
Dữ liệu đảm bảo tổng của ~N~ qua tất cả các bộ dữ liệu là ~10^5~.
Output
Với mỗi trường hợp test, in ra ~N~ số nguyên dương trên một dòng, cách nhau bởi dấu cách. Số thứ ~i~ bạn in ra ứng với số bánh mà Mabư Béo cần xếp trên đĩa có chỉ số thứ ~i~ trong ~N~ đĩa.
Kết quả sẽ được coi là đúng nếu tổng số bánh bạn in ra là ~M~, và thỏa mãn nhiều trường hợp của ~K~ nhất có thể. Nếu tồn tại nhiều đáp án thỏa mãn, in ra đáp án bất kỳ.
Sample Input 1
3
4 12
6 15
1 10000000000
Sample Output 1
4 2 2 4
3 3 1 2 3 3
10000000000
Notes
Trong ví dụ thứ nhất, cách chia của Mabư béo thỏa mãn ~K = 1~, ~K = 2~ và ~K = 3~. Ta có thể chứng minh rằng không tồn tại cách chia nào thỏa mãn cả ~K = 1~, ~K = 2~, ~K = 3~ và ~K = 4~.
Trong ví dụ thứ hai, cách chia của Mabư béo thỏa mãn ~K = 1~ và ~K = 5~. Lưu ý rằng lượng bánh trong mỗi đĩa phải là số dương, do đó cách chia ~(3, 3, 3, 3, 3, 0)~ không được chấp nhận.
Trong ví dụ thứ ba, Mabư chỉ có một cách chia duy nhất và nó thỏa mãn ~K = 1~.
Điểm: 1

|
Mabư Béo đang tập chơi Liên Minh. Một ngày nào đó, hắn muốn gia nhập Đội Tuyển LoL (viết tắt là DTL). |
Liên Minh Huyền Thoại, trong tiếng Anh là League of Legends (LoL), là một tựa game nổi tiếng trên toàn cầu. Có ba chế độ chơi chính: Đấu trường Công Lý, ARAM, và chế độ Quay vòng.
Hôm nay Mabư Béo sẽ chơi ~N~ game. Game thứ ~i~ hắn chơi sẽ thể hiện qua ký tự ~s_i~. ~s_i~ sẽ bằng 'a', hoặc 'b', hoặc 'c', nếu ở game thứ ~i~ hắn chơi Đấu trường Công Lý, hoặc ARAM, hoặc chế độ Quay vòng. Để cho hắn không bao giờ cảm thấy chán, khi viết các ký tự ứng với các game hắn chơi lần lượt nhau và tạo thành một xâu ~s~, hắn ta sẽ phải không được thấy một xâu con có tính chất tự lặp, được định nghĩa như sau:
- Một xâu tự lặp ~s~ là một xâu có độ dài chẵn, lớn hơn ~0~. Nếu đặt ~k = \frac{|s|}{2}~, thì ~s~ phải thỏa mãn ~s[1..k] = s[k+1..|s|]~.
Chẳng hạn: 'abab', 'cc', 'bacbac' là những xâu tự lặp, còn 'abc', 'baab', 'aaa', 'ababab' thì không phải.
Một xâu con được định nghĩa là một xâu tạo bởi ~0~ hoặc một số các ký tự liên tiếp nhau trong xâu đó, giữ nguyên thứ tự trong xâu gốc.
Hãy chỉ cho Mabư Béo một thứ tự chơi ~N~ game bất kỳ, thỏa mãn không xuất hiện một xâu con tự lặp nào trong xâu thứ tự các game mà hắn sẽ chơi.
Input
Mỗi file test chứa nhiều trường hợp test. Dòng đầu của mỗi file chứa số trường hợp test trong file ~T~ (~1 \le T \le 1000~). Mỗi trường hợp test được mô tả như sau:
Một dòng duy nhất chứa một số nguyên: ~N~ (~1 \le N \le 10^6~) - số game mà Mabư Béo sẽ chơi.
Dữ liệu đảm bảo tổng của ~N~ qua tất cả các bộ dữ liệu là ~10^6~.
Output
Với mỗi file test, in ra trên dòng duy nhất, "-1" nếu không thể tạo được xâu thỏa mãn. Ngược lại, in ra một xâu có ~N~ ký tự, chỉ dẫn Mabư Béo cách chọn chế độ cho từng ván chơi. Ký tự thứ ~i~ bằng 'a', 'b', hoặc 'c' thể hiện rằng Mabư cần phải chọn chế độ chơi tương ứng cho ván đấu thứ ~i~ của hắn.
Sample Input 1
2
3
7
Sample Output 1
bcb
abacabc
Notes
Lưu ý rằng, ở test ví dụ đầu tiên, các xâu: 'abc', 'aba', 'cbc' cũng thỏa mãn điều kiện. Mặt khác, các xâu 'aab', 'ccc' thì không, vì lần lượt có những xâu con 'aa' và 'cc' là những xâu tự lặp.
Điểm: 1

|
Mabư Béo là một võ sĩ. Việc luyện tập là điều không thể bỏ qua trong lịch trình hàng ngày của hắn. Hắn có một dàn người máy trong sân tập được tích hợp trí tuệ nhân tạo, có thể đưa ra các đòn đánh gây bất ngờ cho chính hắn. |
Mỗi người máy trang bị theo một hoán vị ~p~ từ ~1~ đến ~N~: ~p_1, p_2, \ldots, p_N~. Hoán vị này định nghĩa ngưỡng sức mạnh của nó (cùng với các đòn đánh, bộ kỹ năng nó có, nhưng điều đó không quá quan trọng trong bài toán này).
Công thức tính ngưỡng sức mạnh của một người máy như sau:
Gọi ~p(i)~ là phần tử thứ ~i~ trong hoán vị ~p~ đi theo người máy. Với mọi số nguyên dương ~k~, ta định nghĩa: ~p^1(x) = p(x)~ và ~p^{k+1}(x) = p(p^{k}(x))~. Khi đó: ~p^1(x) = p(x)~, ~p^2(x) = p(p(x))~, ~p^3(x) = p(p(p(x)))~, ... và tương tự với các số lớn hơn.
Ngưỡng sức mạnh của người máy này, thể hiện bằng số ~G(p)~, chính là số nguyên dương bé nhất thỏa mãn: ~p^{G(p)}(x) = x~ với tất cả số nguyên dương ~x \le N~.
Trong một ngày lười biếng, và phải đối đầu với một trong những người máy mạnh nhất trên sân tập của mình, Mabư Béo tự hỏi, làm thế nào để trong nhiều nhất một lần: đổi chỗ hai vị trí ~i~ và ~j~ (~1 \le i < j \le N~, trong hoán vị ~p~, sao cho ngưỡng sức mạnh của người máy là bé nhất có thể.
Vì đáp số có thể rất lớn, hãy in ra chúng, modulo ~998\ 244\ 353~.
Input
Mỗi file test sẽ chứa nhiều trường hợp test. Dòng đầu tiên chứa số trường hợp test ~T~ (~1 \le T \le 1000~). Mô tả một trường hợp test như sau:
Dòng đầu chứa số nguyên ~N~ (~2 \le N \le 10^4~) - số phần tử trong hoán vị.
Dòng thứ hai chứa ~N~ số nguyên: ~p_1, p_2, \ldots, p_N~ (~1 \le p_i \le N~) - hoán vị tương ứng với người máy đang xét đến.
Dữ liệu đảm bảo rằng tổng của ~N~ qua tất cả trường hợp test sẽ không vượt quá ~10^4~.
Output
Với mỗi trường hợp test, in ra một số nguyên duy nhất trên một dòng, thể hiện sức mạnh tối thiểu của người máy sau khi đổi chỗ hai số trong hoán vị của nó. Kết quả cần được in ra, modulo ~998\ 244\ 353~.
Sample Input 1
8
2
1 2
2
2 1
4
2 1 4 3
3
3 2 1
10
2 1 4 5 3 7 8 9 6 10
7
7 1 2 5 4 3 6
3
1 2 3
8
8 1 2 3 4 5 6 7
Sample Output 1
1
1
2
1
4
4
1
4
Notes
Xét trường hợp ví dụ thứ ~5~. Ban đầu, ta chứng minh được ~G(p) = 12~. Ta có thể chọn đổi chỗ ~p(5) = 3~ và ~p(10) = 10~. Khi đó, ~G(p)~ sẽ giảm xuống còn ~4~.
Điểm: 1

|
Sau những trận đánh tay đôi bất phân thắng bại với loài người, đặc biệt là những tay võ nghệ cao cường như sư phụ Son Goku, Mabư Béo quyết định giải quyết mâu thuẫn trong trò chơi Đế chế. |
Vùng đất của Son Goku có ~N~ căn nhà trên mặt phẳng tọa độ hai chiều. Căn nhà thứ ~i~ được thể hiện bằng một điểm, có tọa độ ~(x_i, y_i)~.
Dẫu cho có một bàn tay mũm mĩm hơn rất nhiều, trí thông minh cùng độ thông hiểu game của Mabư Béo đã giúp hắn có một mảnh đất lớn mạnh hơn rất nhiều. Bằng chứng là vùng đất của Mabư hiện đã vây quanh các phía Đông, Tây, Bắc của vùng đất thuộc về Son Goku. Và nếu để xảy ra sơ hở, các căn nhà ở gần biên giới giữa hai vùng đất có thể bị đánh chiếm bất kỳ lúc nào.
Mỗi ngày, Mabư Béo sẽ chọn và đánh chiếm một căn nhà năm trên "ranh giới" giữa hai vùng đất. Cụ thể hơn, hắn ta sẽ chọn ra một căn nhà thỏa mãn một trong các điều kiện sau:
Nằm ở ngoài cùng phía Bắc (có tung độ lớn nhất) trong các căn nhà còn lại của Goku.
Nằm ở ngoài cùng phía Tây (có hoành độ nhỏ nhất) trong các căn nhà còn lại của Goku.
Nằm ở ngoài cùng phía Đông (có hoành độ lớn nhất) trong các căn nhà còn lại của Goku.
Nếu trong một ngày nào đó Mabư Béo có nhiều lựa chọn, hắn ta có thể chọn một căn nhà tùy ý hắn. Hắn ta có thể dừng lại bất cứ lúc nào khi thấy đã quá đủ để khẳng định vị thế của bản thân trên đấu trường phím chuột.
Hỏi: hãy đếm số bản kế hoạch đánh chiếm khác nhau của Mabư Béo trên vùng đất của Son Goku. Vì con số có thể rất lớn, hãy in ra phần dư của nó cho ~998244353~.
Cụ thể hơn, hai bản kế hoạch đánh chiếm được cho là khác nhau, khi và chỉ khi tồn tại ít nhất một căn nhà bị đánh chiếm xuất hiện trong một bản kế hoạch, nhưng không tồn tại trong bản kế hoạch còn lại.
Input
Dòng đầu tiên chứa ~N~ (~1 \le N \le 2 \times 10^5~) - số căn nhà trong vùng đất của Son Goku.
~N~ dòng tiếp theo, dòng thứ ~i~ chứa hai số nguyên: ~x_i~ và ~y_i~ (~|x_i|, |y_i| \le 10^9~), tọa độ của căn nhà thứ ~i~.
Dữ liệu đảm bảo không tồn tại hai căn nhà nào có cùng tọa độ. Nói cách khác: với mọi cặp ~(i, j)~ thỏa mãn ~1 \le i < j \le N~, ~x_i \neq x_j~ hoặc ~y_i \neq y_j~.
Output
In ra một số nguyên duy nhất: số kế hoạch đánh chiếm nhà của Mabư Béo, modulo ~998244353~.
Sample Input 1
3
0 1
1 0
2 2
Sample Output 1
7
Sample Input 2
4
-1 0
1 0
-2 1
2 1
Sample Output 2
11
Notes
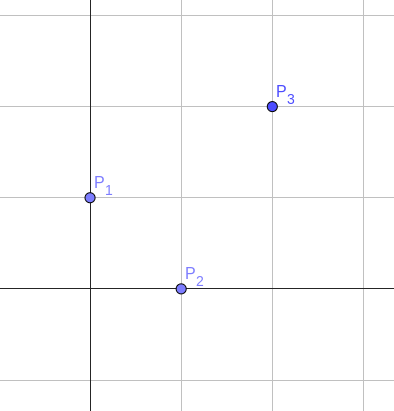
Trong ví dụ thứ nhất, có ~2^3 = 8~ kế hoạch chiếm thành phố, trong đó chỉ có kế hoạch đánh chiếm duy nhất thành phố ~2~ là không khả thi (do thành phố ~2~ không nằm ở ngoài cùng phía Bắc, Tây hay Đông).
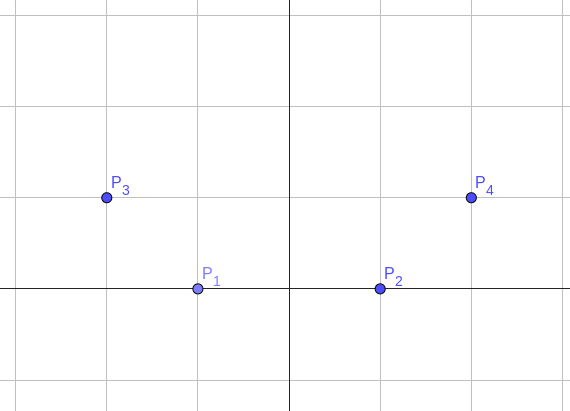
Trong ví dụ thứ hai, những kế hoạch không khả thi bao gồm: ~\{1\}~, ~\{2\}~, ~\{1, 2\}~, ~\{1, 4\}~ và ~\{2, 3\}~.
Điểm: 1

|
Để tìm lại Bảy Viên Ngọc Rồng, Mabư Béo cần phải trải qua một hành trình dài, gian nan, khúc khuỷu. |
Hắn đang cầm trên tay bản đồ của Vương quốc DTL hiện tại hắn đang đứng trên. Bản đồ có thể được thể hiện bởi mặt phẳng có trục tọa độ ~Oxy~, với vương quốc DTL trải dài theo hoành độ và tung độ, đều từ ~-10^4~ đến ~10^4~. Mỗi điểm ~(x, y)~ đều có một độ cao, được định nghĩa bởi hàm ~H(x, y)~. ~H(x, y)~ có dạng ~P(x) + Q(y)~. Trong đó: ~P(x)~ là một đa thức biến ~x~, có bậc tối đa là ~3~, và ~Q(y)~ là một đa thức biến ~y~, có bậc tối đa là ~3~.
Mabư Béo có thể tự do di chuyển trên thế giới này: đi bộ, leo trèo đến một vị trí gần vị trí hắn đang đứng, hay lên máy bay, hoặc dùng phép tele đến ở một vị trí rất xa, bất kỳ ở trong vương quốc DTL. Tất nhiên, hắn không muốn di chuyển ra ngoài vương quốc, vì hắn biết cả 7 viên Ngọc Rồng đều đang nằm đâu đó ở nơi này.
Tuy nhiên, vì không khí loãng, cùng nỗi sợ độ cao, hắn sẽ không thể tới thăm các điểm mà có độ cao bằng ~C~ hoặc hơn. Khi đó, tồn tại các "Vùng nguy hiểm" hắn đã vẽ ra trên hành trình của mình.
Cho mô tả của hàm ~H(x, y)~, hãy đếm xem có bao nhiêu Vùng nguy hiểm. Hai điểm được cho là cùng một vùng nguy hiểm nếu như tồn tại một đường đi bộ nối hai điểm với nhau, mà tất cả các điểm trên đường đi đó đều thuộc vùng nguy hiểm.
Input
Mỗi file test chứa nhiều trường hợp test. Dòng đầu của mỗi file chứa số trường hợp test trong file ~T~ (~1 \le T \le 10^5~). Mỗi trường hợp test được mô tả như sau:
Dòng thứ nhất chứa ~4~ số nguyên: ~a_{x}~, ~b_{x}~, ~c_{x}~, ~d_{x}~ (~-100 \le a_x, b_x, c_x, d_x \le 100~) – thể hiện hàm ~P(x)~. ~P(x) = a_{x} \cdot x^3 + b_{x} \cdot x^2 + c_{x} \cdot x + d_{x}~.
Dòng thứ hai chứa ~4~ số nguyên: ~a_{y}~, ~b_{y}~, ~c_{y}~, ~d_{y}~ (~-100 \le a_y, b_y, c_y, d_y \le 100~) – thể hiện hàm ~Q(y)~. ~Q(y) = a_{y} \cdot y^3 + b_{y} \cdot y^2 + c_{y} \cdot y + d_{y}~.
Dòng thứ ba chứa số thực ~C~ (~|C| \le 10^{18}~).
Output
Với mỗi trường hợp test, in ra trên một dòng một số nguyên duy nhất: số Vùng nguy hiểm mà Mabư Béo không thể di chuyển đến.
Sample Input 1
2
0 1 0 0
0 1 0 0
200000000
1 1 1 1
-1 -1 -1 -1
0
Sample Output 1
4
1
Notes
Ở ví dụ đầu tiên, hàm ~H(x, y) = x^2 + y^2~. Mabư Béo không thể ghé thăm ~4~ góc ngoài cùng của vương quốc.