[Mirror] VNOI CUP 2024 - Qualification Round 2
Điểm: 500
Nhân loại đang gặp nguy hiểm vì những con quái vật đến từ không gian. Trong tình huống khó khăn này, một siêu anh hùng đã xuất hiện để giải cứu nhân loại khỏi ~n~ con quái vật.
Ban đầu, siêu anh hùng có chỉ số sức mạnh là ~x~. Ở bước thứ ~i~, siêu anh hùng có thể:
Chọn một con quái vật chưa bị tiêu diệt sao cho chỉ số máu của quái vật không vượt quá chỉ số sức mạnh của anh hùng.
Nếu anh hùng chọn được một con quái vật như vậy, con quái vật này sẽ bị tiêu diệt và chỉ số sức mạnh của anh hùng được tăng lên ~i + 1~ lần; ngược lại, chỉ số sức mạnh của anh hùng giữ nguyên.
Chỉ số máu của các con quái vật chưa bị tiêu diệt tăng lên ~i~ lần, bất kể anh hùng có vừa tiêu diệt được con quái nào hay không.
Hãy tính xem siêu anh hùng có thể tiêu diệt tối đa bao nhiêu con quái vật.
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên chứa số lượng test case ~t~ (~1 \leq t \leq 100~). Mô tả của mỗi test case như sau.
Dòng đầu tiên chứa hai số nguyên dương ~n~ và ~x~ (~1 \le n \le 5000~, ~1 \le x \le 10^{12}~) — số lượng các con quái vật và chỉ số sức mạnh ban đầu của siêu anh hùng.
Dòng thứ hai chứa ~n~ số nguyên dương ~a_1, a_2, ..., a_n~ (~1 \le a_i \le 10^{12}~) — chỉ số máu ban đầu của các con quái vật.
Đảm bảo rằng tổng của ~n~ qua tất cả các test case không vượt quá ~5000~.
Output
Với mỗi test case, in ra một số nguyên duy nhất — số con quái vật tối đa anh hùng có thể tiêu diệt.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~250~ | ~1 \le x, a_i \le 100~; tổng của ~n~ không vượt quá ~100~ |
| 2 | ~250~ | Không có giới hạn gì thêm |
| Tổng | ~500~ |
Sample Input 1
2
5 3
1 1 1 1 50
3 2
7 1 1
Sample Output 1
4
2
Notes
Dưới đây là giải thích cho test case đầu tiên, với ký hiệu ~-~ đại diện cho quái vật đã bị tiêu diệt.
Anh hùng chọn quái vật đầu tiên. Sau khi anh hùng tiêu diệt quái vật đầu tiên, các quái vật còn lại có chỉ số máu là ~[-, 1, 1, 1, 50]~. Chỉ số sức mạnh của anh hùng là ~6~.
Anh hùng chọn quái vật thứ hai. Sau khi anh hùng tiêu diệt quái vật thứ hai, các quái vật còn lại có chỉ số máu là ~[-, -, 2, 2, 100]~. Chỉ số sức mạnh của anh hùng là ~18~.
Anh hùng chọn quái vật thứ ba. Sau khi anh hùng tiêu diệt quái vật thứ ba, các quái vật còn lại có chỉ số máu là ~[-, -, -, 6, 300]~. Chỉ số sức mạnh của anh hùng là ~72~.
Anh hùng chọn quái vật thứ tư. Sau khi anh hùng tiêu diệt quái vật thứ tư, quái vật còn lại có chỉ số máu là ~[-, -, -, -, 1200]~. Chỉ số sức mạnh của anh hùng là ~360~.
Không còn quái vật nào có thể bị tiêu diệt nữa.
Điểm: 1250
Có ~n~ lỗ bi trên nằm cách đều nhau trên một đường tròn. Các lỗ được đánh số từ ~1~ đến ~n~ theo chiều kim đồng hồ. Đồng thời, có một lỗ đựng bi nằm ở tâm đường tròn được đánh số ~n+1~.
Ban đầu, với ~n~ lỗ bi nằm trên đường tròn thì lỗ ~i~ chứa đúng một viên bi có màu ~a_i~, còn lỗ ~n+1~ là lỗ trống. Các viên bi có màu từ ~1~ đến ~n~, không có hai viên bi nào cùng màu. Bạn có thể di chuyển viên bi từ một lỗ đang chứa bi đến một lỗ trống nếu hai lỗ bi đó nằm liên tiếp nhau trên đường tròn, hoặc một trong hai lỗ bi là lỗ ~n+1~.
Hãy tìm dãy thao tác chuyển bi sao cho bi màu ~i~ về đúng với lỗ ~i~, đồng thời số thao tác không vượt quá ~1500~.
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên chứa số lượng test case ~t~ (~1 \leq t \leq 50~). Mô tả của mỗi test case như sau.
Dòng đầu tiên chứa số nguyên ~n~ (~3 \le n \le 50~) – số lỗ bi nằm trên đường tròn.
Dòng thứ hai gồm ~n~ số nguyên ~a_1, a_2, \ldots, a_n~ (~1 \le a_i \le n~) – màu của viên bi nằm trên ~n~ lỗ bi nằm trên đường tròn. Dữ liệu vào đảm bảo mỗi màu bi sẽ xuất hiện đúng một lần.
Output
Với mỗi test case, hãy in ra đáp án theo định dạng như sau:
Dòng đầu tiên in ra số nguyên ~k~ (~0 \le k \le 1500~) – số thao tác di chuyển bi cần thực hiện.
Dòng thứ ~i~ trong ~k~ dòng tiếp theo in ra hai số nguyên ~s_i~ và ~t_i~ (~1 \le s_i, t_i \le n+1~, ~s_i \ne t_i~) mô tả thao tác di chuyển bi thứ ~i~ (từ lỗ ~s_i~ sang lỗ ~t_i~). Lỗ ~s_i~ phải chứa một viên bi, và lỗ ~t_i~ phải trống.
Có thể chứng minh rằng luôn tồn tại một cách di chuyển bi thỏa yêu cầu đề bài.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~500~ | ~n \le 6~ |
| 2 | ~500~ | ~n \le 25~ |
| 3 | ~250~ | Không có ràng buộc gì thêm |
| Tổng | ~1250~ |
Sample Input 1
2
3
2 3 1
3
1 2 3
Sample Output 1
4
3 4
2 3
1 2
4 1
0
Notes
Với test case thứ nhất, hình vẽ bên dưới minh họa một cách di chuyển bi thỏa yêu cầu đề bài. Số ghi bên ngoài lỗ bi cho biết số thứ tự của lỗ bi, số ghi bên trong cho biết màu của viên bi trong lỗ.
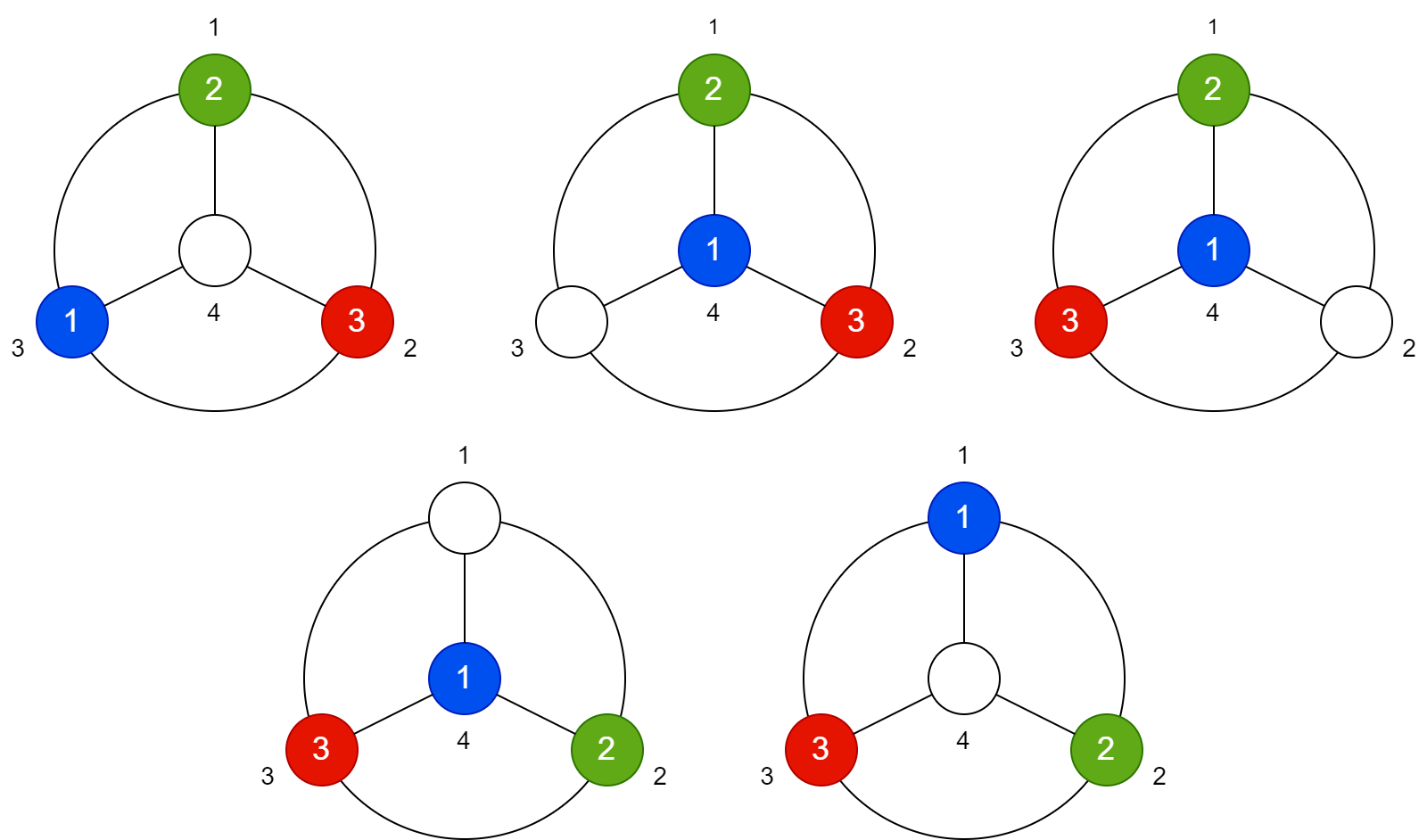
Hình vẽ minh họa ví dụ thứ nhất.
Với test case thứ hai, các viên bi đều đã ở đúng ô bi nên ta không cần thực hiện thao tác di chuyển bi nào.
Sau khi nhận ra bài cũ quá khó với vị trí là bài thứ ba của vòng loại thứ hai của VNOI CUP, ban ra đề đã tức tốc nghĩ ra bài toán sau.
Cho hai mảng số nguyên ~a~ và ~c~ cùng có độ dài ~n~, bạn hãy tìm giá trị nhỏ nhất của biểu thức sau, với ~x~ là một giá trị nguyên tùy chọn:
$$\sum_{i=1}^n c_i \cdot |a_i - x|$$
Tuy nhiên, ban ra đề vẫn không biết cách giải bài này. Các bạn hãy giúp ban ra đề nhé!
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên chứa số lượng test case ~t~ (~1 \leq t \leq 10\,000~). Mô tả của mỗi test case như sau.
Dòng đầu tiên chứa số nguyên ~n~ (~1 \le n \le 3 \cdot 10^5~) — độ dài của mảng ~a~ và ~c~.
Dòng thứ hai chứa ~n~ số nguyên ~a_1, a_2, \ldots, a_n~ (~-10^6 \le a_i \le 10^6~) — các phần tử của mảng ~a~.
Dòng thứ ba chứa ~n~ số nguyên ~c_1, c_2, \ldots, c_n~ (~-10^6 \le c_i \le 10^6~) — các phần tử của mảng ~c~.
Đảm bảo rằng tổng của ~n~ qua tất cả các test case không vượt quá ~3 \cdot 10^5~.
Output
Với mỗi test case, nếu giá trị của biểu thức có thể xuống tới âm vô cùng, in ra xâu ~\texttt{-inf}~. Nếu không, hãy in ra số nguyên là giá trị nhỏ nhất của biểu thức trên.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~500~ | ~c_i = 1~ với mọi ~1 \le i \le n~ |
| 2 | ~500~ | ~c_i \ge 0~ với mọi ~1 \le i \le n~ |
| 3 | ~500~ | Không có ràng buộc gì thêm |
| Tổng | ~1500~ |
Sample Input 1
4
6
1 2 3 4 5 6
1 1 1 1 1 1
6
-4 -2 0 2 4 6
-1 -1 -1 -1 -1 -1
3
-100 0 100
1 0 -1
10
2 -8 4 -8 7 8 -1 -5 -7 -6
2 0 10 10 9 -4 -10 9 2 7
Sample Output 1
9
-inf
-200
158
Notes
Ở test case đầu tiên, với ~x = 3~, giá trị của biểu thức là ~9~. Ta có thể chứng minh là không có giá trị ~x~ nào có thể làm biểu thức bé hơn ~9~.
Ở test case thứ hai, với ~x~ tiến tới ~\infty~, giá trị của biểu thức tiến tới ~-\infty~.
Đã sống gần hai mươi năm trên đời mà vẫn chưa có người yêu, Trung quyết định lên chùa cầu duyên. Sau khi thực hiện đủ các nghi lễ, Trung được nhận một tấm bùa. Trên tấm bùa ghi một xâu độ dài ~n~ chỉ gồm hai chữ cái ~\texttt{O}~ hoặc ~\texttt{K}~. Với hiểu biết uyên thâm về bủa ngải của mình, Trung biết rằng độ hiệu nghiệm của tấm bùa phụ thuộc vào các cặp chữ cái liên tiếp nhau. Cụ thể:
Cặp chữ ~\texttt{OK}~ có tác dụng, do đó, nếu tấm bùa có ~a~ cặp chữ ~\texttt{OK}~ thì độ hiệu nghiệm của tấm bùa sẽ tăng lên ~a^2~.
Cặp chữ ~\texttt{KO}~ phản tác dụng, do đó, nếu tấm bùa có ~b~ cặp chữ ~\texttt{KO}~ thì độ hiệu nghiệm của tấm bùa sẽ giảm đi ~b^2~.
Nói cách khác, nếu tấm bùa có ~a~ cặp chữ ~\texttt{OK}~ và ~b~ cặp chữ ~\texttt{KO}~ thì độ hiệu nghiệm của tấm bùa sẽ là ~a^2 - b^2~. Ví dụ, nếu tấm bùa ghi xâu ~\texttt{OOOKOO}~ thì ~a = 1~, ~b = 1~, do vậy độ hiệu nghiệm của tấm bùa sẽ là ~1^2 - 1^2 = 0~.
Trung chưa hài lòng lắm về tấm bùa của mình, nên đã xin nhà chùa phát cho một tấm bùa khác. Tuy nhiên, nhà chùa chỉ cho phép Trung thay đổi tấm bùa hiện tại tối đa ~k~ lần, mỗi lần Trung có thể chọn hai chữ cái bất kì trên tấm bùa và đổi chỗ chúng cho nhau. Hãy giúp Trung có được tấm bùa yêu với độ hiệu nghiệm lớn nhất có thể nhé!
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên chứa số lượng test case ~t~ (~1 \leq t \leq 10\,000~). Mô tả của mỗi test case như sau.
Dòng đầu tiên gồm hai số nguyên dương ~n~ và ~k~ (~2 \leq n \leq 10^5~, ~1 \leq k \leq 10~) — độ dài của xâu được ghi trên tấm bùa và số lần biến đổi tối đa.
Dòng thứ hai gồm một xâu ~s~ gồm ~n~ kí tự ~\texttt{O}~ hoặc ~\texttt{K}~, mô tả xâu được ghi trên tấm bùa.
Đảm bảo rằng tổng ~n~ của tất cả các test case không vượt quá ~10^5~.
Output
Với mỗi test case, in ra một số nguyên là độ hiệu nghiệm tối đa tấm bùa có thể đạt được.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~250~ | Tổng của ~n~ không vượt quá ~100~, ~k = 1~ |
| 2 | ~750~ | ~k = 1~ |
| 3 | ~1250~ | Không có ràng buộc gì thêm |
| Tổng | ~2250~ |
Sample Input 1
5
2 1
KO
2 1
OK
7 1
OOOKKKK
7 1
KKOOKKK
10 2
KOOKOKKKOO
Sample Output 1
1
1
5
3
9
Notes
Ở test case thứ nhất, cách biến đổi tối ưu là ~\mathtt{KO}~ ~\to \mathtt{OK}~. Xâu thu được cuối cùng có độ hiệu nghiệm là ~1~.
Ở test case thứ hai, cách biến đổi tối ưu là giữ nguyên xâu ~\mathtt{OK}~, với độ hiệu nghiệm là ~1~.
Ở test case thứ năm, một cách biến đổi tối ưu là ~\mathtt{KO}~~\mathtt{OKOKKKOO} \to \mathtt{OKOKOK}~~\texttt{K}~~\texttt{KO}~~\texttt{O}~ ~\to \mathtt{OKOKOKOKOK}~, thu được xâu cuối cùng có độ hiệu nghiệm là ~9~.
Điểm: 2500
Một công ty nọ có ~n~ văn phòng được đánh số từ ~1~ đến ~n~. Công ty này muốn lắp đặt một vài đường dây liên lạc hai chiều giữa các văn phòng, sao cho giữa mọi cặp văn phòng ~i~, ~j~ (~i \neq j~) tồn tại ít nhất một đường liên lạc giữa chúng.
Có ~k~ nhà mạng cung cấp tổng cộng ~m~ đường dây liên lạc, trong đó đường dây thứ ~i~ kết nối văn phòng ~u_i~ và văn phòng ~v_i~, được vận hành bởi nhà mạng ~c_i~ và mất chi phí ~p_i~ đồng~^\dagger~ để lắp đặt (lưu ý mỗi cặp văn phòng có thể có đường dây của nhiều nhà mạng).
Ngoài ra, để tăng tính cạnh tranh, cả ~k~ nhà mạng đều đang tổ chức chương trình tri ân khách hàng; cụ thể, nếu tổng chi phí lắp đặt mà công ty trả cho nhà mạng thứ ~j~ vượt quá ~s_j~ đồng, nhà mạng ~j~ sẽ giảm giá ~50\%~ cho phần chi phí chênh lệch, nghĩa là công ty sẽ chỉ phải trả ~x_j - \frac{\max(0, x_j - s_j)}{2}~ đồng, với ~x_j~ là tổng chi phí trước khi áp dụng khuyến mãi.
Hãy tìm cách dựng mạng lưới liên lạc sao cho tổng chi phí là nhỏ nhất có thể. Vì ta có thể chứng minh là tổng chi phí nhỏ nhất nhân ~2~ là một số nguyên, bạn cần in ra tổng chi phí nhỏ nhất nhân ~2~.
~^\dagger~ ~1~ triệu đồng tương đương khoảng ~420~ Krone Na Uy.
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên chứa số lượng test case ~t~ (~1 \leq t \leq 100~). Mô tả của mỗi test case như sau.
Dòng đầu tiên gồm ba số nguyên dương ~n~, ~m~, ~k~ (~2 \leq n \leq 1000~, ~n - 1 \leq m \leq 5 \cdot 10^5~, ~1 \leq k \leq 10~) — số lượng văn phòng của công ty, số lượng đường dây có thể lắp đặt, và số lượng nhà mạng.
Dòng thứ ~i~ trong ~m~ dòng tiếp theo gồm bốn số nguyên dương ~u_i~, ~v_i~, ~c_i~, ~p_i~ (~1 \leq u_i, v_i \leq n~, ~u_i \neq v_i~, ~1 \leq c_i \leq k~, ~1 \leq p_i \leq 10^9~), mô tả đường dây thứ ~i~.
Dòng cuối cùng gồm ~k~ số nguyên dương ~s_1, s_2, \cdots, s_k~ (~1 \leq s_i \leq 10^9~), mô tả chi tiết chương trình tri ân khách hàng của ~k~ nhà mạng.
Mỗi test case đảm bảo tồn tại ít nhất một cách dựng mạng lưới liên lạc kết nối tất cả ~n~ văn phòng.
Đảm bảo rằng tổng của ~n~ qua tất cả các test case không vượt quá ~1000~, và tổng của ~m~ không vượt quá ~5 \cdot 10^5~.
Output
Với mỗi test case, in ra một số nguyên là tổng chi phí nhỏ nhất để dựng mạng lưới liên lạc nhân ~2~.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~500~ | ~k = 1~ |
| 2 | ~1000~ | ~k \le 2~ |
| 3 | ~1000~ | Không có ràng buộc gì thêm |
| Tổng | ~2500~ |
Sample Input 1
4
3 4 2
1 2 1 3
2 3 1 5
1 2 2 4
1 3 2 4
5 6
3 4 2
1 2 1 3
2 3 1 5
1 2 2 4
1 3 2 4
1 1
5 7 3
1 5 3 100
1 2 1 5
4 5 1 5
1 3 2 7
2 3 3 10
1 2 2 4
4 5 2 4
5 20 100
2 3 3
1 2 1 5
1 2 2 6
1 2 3 7
6 2 2
Sample Output 1
13
9
225
8
Notes
Với test case thứ nhất, hình minh họa bên dưới biểu diễn các đường dây kết nối được phép lắp đặt, với các đường dây màu đỏ thuộc nhà mạng thứ ~1~ và đường dây màu xanh thuộc nhà mạng thứ ~2~. Với ~s = [5, 6]~, ta nên lắp đặt các đường dây được tô đậm. Tổng chi phí trước khuyến mãi phải chi cho nhà mạng thứ ~1~ và thứ ~2~ lần lượt là ~[8, 0]~, nên tổng chi phí sau khuyến mãi là ~\left(8 - \frac{\max(0, 8 - 5)}{2}\right) + \left(0 - \frac{\max(0, 0 - 6)}{2}\right) = \frac{13}{2}~.
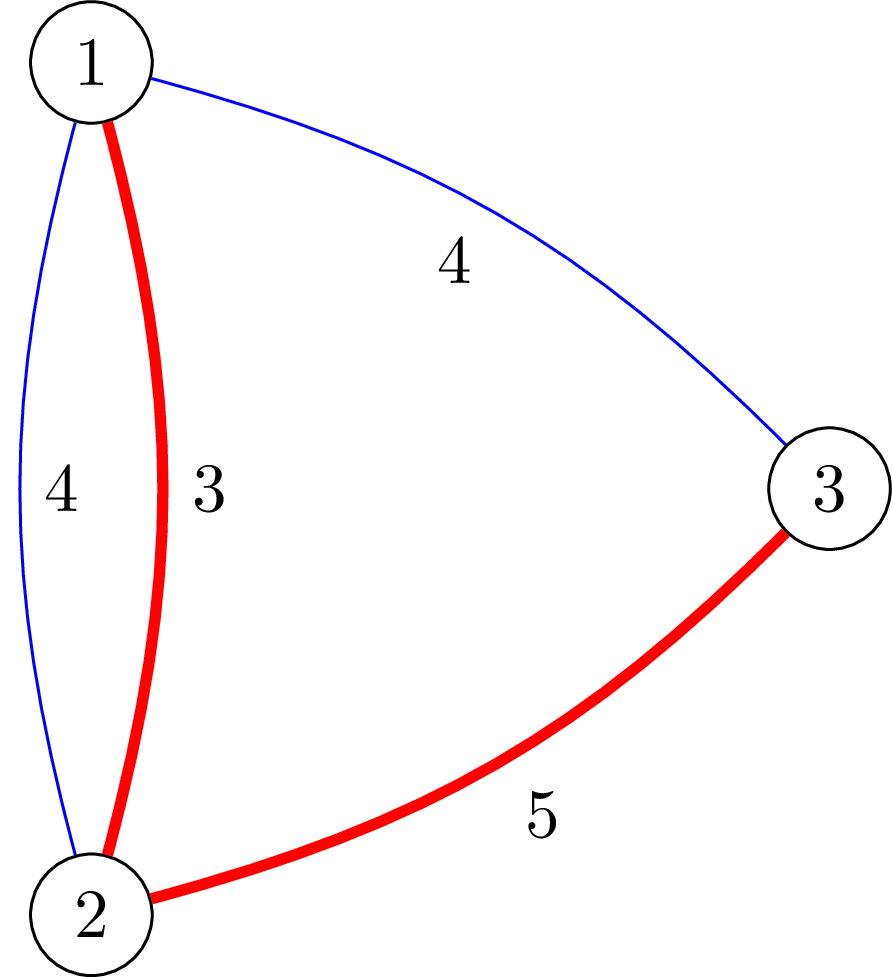
Hình minh họa ví dụ thứ nhất.
Với test case thứ hai, các đường dây được phép lắp đặt tương tự như test case thứ nhất. Với ~s = [1, 1]~, ta nên lắp đặt các đường dây được tô đậm. Tổng chi phí trước khuyến mãi phải chi cho nhà mạng thứ ~1~ và thứ ~2~ lần lượt là ~[3, 4]~, nên tổng chi phí sau khuyến mãi là ~\left(3 - \frac{\max(0, 3 - 1)}{2}\right) + \left(4 - \frac{\max(0, 4 - 1)}{2}\right) = \frac{9}{2}~.
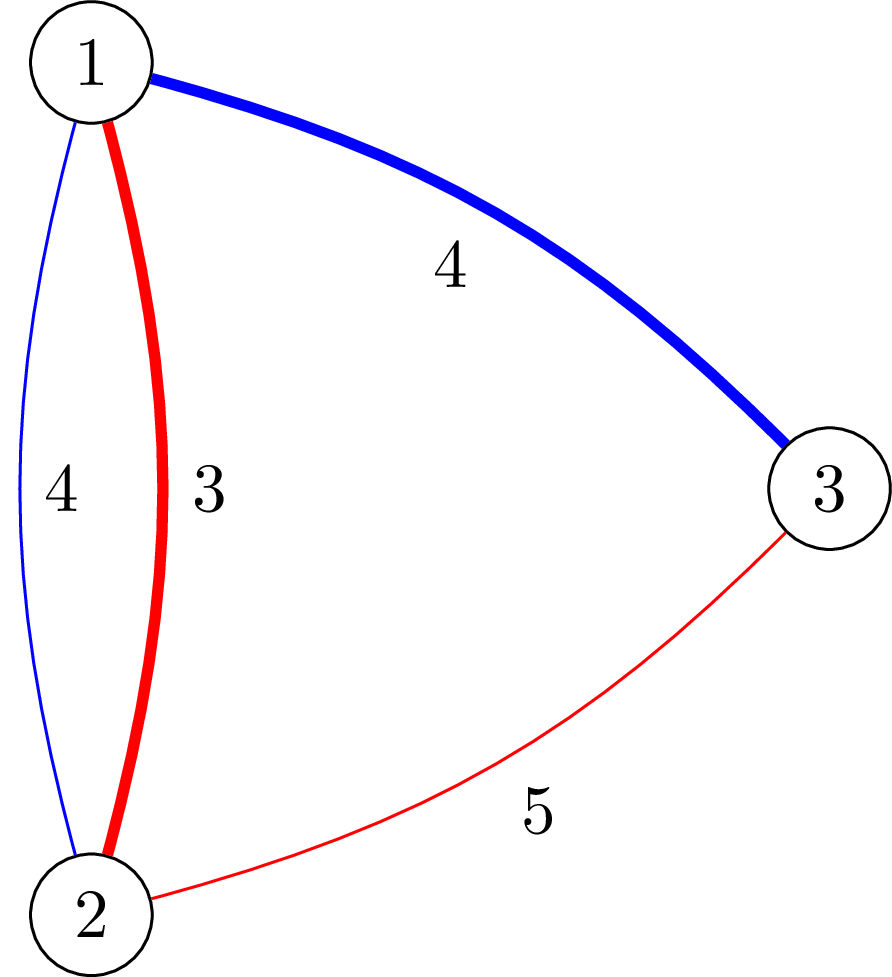
Hình minh họa ví dụ thứ hai.
Cho một đồ thị có hướng ~G~ bao gồm ~n~ đỉnh và ~m~ cạnh, trong đó cạnh thứ ~i~ nối từ đỉnh ~u_i~ tới đỉnh ~v_i~. Ngoài ra, bạn được cho thêm một đường đi ~P~ từ đỉnh ~1~ tới đỉnh ~n~ ~^\dagger~, sử dụng các cạnh thứ ~p_1, p_2, \ldots, p_k~ theo đúng thứ tự đó.
Bạn cần tìm số lượng cạnh ít nhất cần được xóa đi khỏi ~G~ để ~P~ trở thành đường đi duy nhất từ đỉnh ~1~ tới đỉnh ~n~. Nếu không có cách nào xóa cạnh để thỏa mãn điều kiện trên, hãy in ra ~-1~.
~^\dagger~ Một đường đi ~P~ từ đỉnh ~1~ tới đỉnh ~n~ là một danh sách các chỉ số cạnh ~p_1, p_2, \dots, p_k~ sao cho:
~u_{p_1} = 1~.
~v_{p_i} = u_{p_{i + 1}}~ với mọi ~1 \le i < k~.
~v_{p_k} = n~.
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên chứa số lượng test case ~t~ (~1 \leq t \leq 10\,000~). Mô tả của mỗi test case như sau.
Dòng đầu tiên chứa ba số nguyên ~n~, ~m~, và ~k~ (~2 \le n \le 10^5~, ~1 \le m, k \le 10^5~) — số lượng đỉnh và cạnh của đồ thị ~G~, và số lượng cạnh trong đường đi ~P~.
Dòng thứ ~i~ trong ~m~ dòng tiếp theo chứa hai số nguyên ~u_i~ và ~v_i~ (~1 \le u_i, v_i \le n~, ~u_i \neq v_i~) — cạnh thứ ~i~ của đồ thị ~G~.
Dòng tiếp theo chứa ~k~ số nguyên ~p_1, p_2, \ldots, p_k~ (~1 \le p_i \le m~) biểu diễn một đường đi từ ~1~ tới ~n~. Dữ liệu đảm bảo rằng các chỉ số cạnh này tạo thành một đường đi từ đỉnh ~1~ tới đỉnh ~n~.
Đảm bảo rằng tổng của ~n~, tổng của ~m~, và tổng của ~k~ qua tất cả các test case không vượt quá ~10^5~.
Output
Với mỗi test case, in ra một số nguyên là số lượng cạnh ít nhất cần được xóa đi để ~P~ trở thành đường đi duy nhất từ đỉnh ~1~ tới đỉnh ~n~. Nếu không có cách nào xóa cạnh để thỏa mãn điều kiện trên, hãy in ra ~-1~.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~1000~ | ~n = m~, ~G~ liên thông yếu ~^\ddagger~ |
| 2 | ~500~ | Tổng của ~n~ không vượt quá ~1000~, ~k = 1~, ~u_i \neq n~ và ~v_i \neq 1~ với mọi ~1 \le i \le m~ |
| 3 | ~1250~ | Tổng của ~n~ không vượt quá ~1000~ |
| 4 | ~500~ | Không có ràng buộc gì thêm |
| Tổng | ~3250~ |
~^\ddagger~ Một đồ thị có hướng được gọi là liên thông yếu nếu sau khi thay thế tất cả các cạnh có hướng thành cạnh vô hướng, đồ thị trở nên liên thông.
Sample Input 1
3
5 5 4
1 3
3 2
4 3
2 4
4 5
1 2 4 5
5 6 3
1 2
2 3
3 5
3 1
4 3
1 4
6 5 3
5 5 5
1 2
2 3
3 4
4 2
2 5
1 2 3 4 5
Sample Output 1
1
2
-1
Notes
Đối với test case đầu tiên, hình dưới sau đây minh họa đồ thị ~G~, với đường đi ~P~ được tô đỏ. Ta cần xóa cạnh ~4 \to 3~, vì có đường đi ~1 \to 3 \to 2 \to 4 \to 3 \to 2 \to 4 \to 5~ sử dụng cạnh này và đi từ ~1~ đến ~5~.

Minh họa cho test case đầu tiên.
Đối với test case thứ hai, hình dưới sau đây minh họa đồ thị ~G~, với đường đi ~P~ được tô đỏ. Ta cần xóa cạnh ~2 \to 3~ và cạnh ~3 \to 1~.
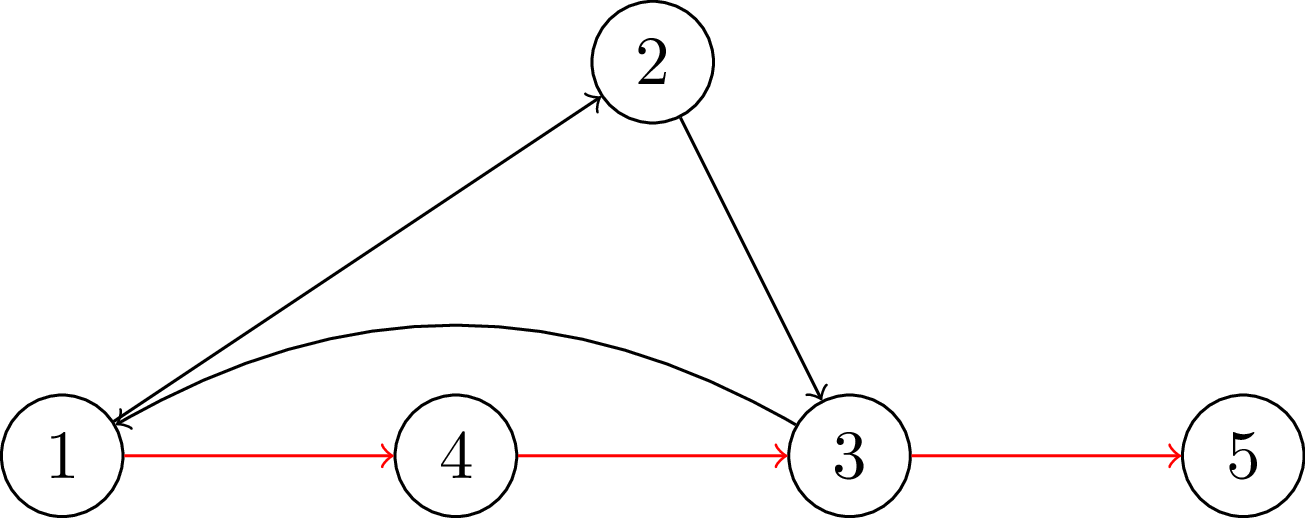
Minh họa cho test case thứ hai.
Điểm: 4000
Bạn được cho một số nguyên dương chẵn ~n~, đồng thời là ~k~ cặp số ~(l_i, r_i)~ thỏa mãn điều kiện ~1 \le l_1 < r_1 < l_2 < r_2 < \ldots < l_k < r_k \le n~. Hãy đếm số lượng xâu ngoặc đúng~^\dagger~ ~s~ có độ dài ~n~ thỏa mãn điều kiện sau, modulo ~998\,244\,353~:
- Với mọi ~1 \le i \le k~, ~s_{l_i} \neq s_{r_i}~.
~^\dagger~ Một xâu ~s~ được tạo thành từ hai loại kí tự ~\mathtt{(}~ và ~\mathtt{)}~ được gọi là xâu ngoặc đúng nếu ~s~ thỏa mãn một trong ba điều kiện sau:
~s~ rỗng.
~s~ có dạng "~\mathtt{(} t \mathtt{)}~", với ~t~ cũng là xâu ngoặc đúng.
~s~ có dạng "~ab~", với ~a~ và ~b~ là hai xâu ngoặc đúng.
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên chứa số lượng test case ~t~ (~1 \leq t \leq 10\,000~). Mô tả của mỗi test case như sau.
Dòng đầu tiên chứa hai số nguyên ~n~ và ~k~ (~2 \le n \le 2 \cdot 10^5~, ~n~ chẵn, ~0 \le k \le \frac{n}{2}~) — độ dài của xâu ~s~ và số được cặp số được cho.
Dòng thứ ~i~ trong ~k~ dòng tiếp theo chứa hai số nguyên ~l_i~ và ~r_i~ biểu diễn cặp số thứ ~i~ được cho. Đảm bảo rằng điều kiện ~1 \le l_1 < r_1 < l_2 < r_2 < \ldots < l_k < r_k \le n~ được thỏa mãn.
Đảm bảo rằng tổng của ~n~ qua tất cả các test case không vượt quá ~2 \cdot 10^5~.
Output
Với mỗi test case, in ra một số nguyên là số lượng xâu ngoặc đúng ~s~ thỏa mãn điều kiện đề bài, modulo ~998\,244\,353~.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~1000~ | Tổng của ~n~ không vượt quá ~2000~ |
| 2 | ~1500~ | ~l_i + 1 = r_i~ với mọi ~1 \le i \le k~ |
| 3 | ~1500~ | Không có ràng buộc gì thêm |
| Tổng | ~4000~ |
Sample Input 1
5
6 0
4 2
1 2
3 4
8 1
1 8
8 2
1 3
5 8
20 4
2 8
9 10
15 17
19 20
Sample Output 1
5
1
14
3
692
Notes
Ở test case đầu tiên, các xâu hợp lệ là ~\mathtt{((()))}~, ~\mathtt{(()())}~, ~\mathtt{(())()}~, ~\mathtt{()(())}~, ~\mathtt{()()()}~.
Ở test case thứ hai, xâu duy nhất hợp lệ là ~\mathtt{()()}~.
Ở test case thứ tư, các xâu hợp lệ là ~\mathtt{(())(())}~, ~\mathtt{(())()()}~, ~\mathtt{(()(()))}~.