Phong tỏa
Xem dạng PDFCho một đồ thị có hướng ~G~ bao gồm ~n~ đỉnh và ~m~ cạnh, trong đó cạnh thứ ~i~ nối từ đỉnh ~u_i~ tới đỉnh ~v_i~. Ngoài ra, bạn được cho thêm một đường đi ~P~ từ đỉnh ~1~ tới đỉnh ~n~ ~^\dagger~, sử dụng các cạnh thứ ~p_1, p_2, \ldots, p_k~ theo đúng thứ tự đó.
Bạn cần tìm số lượng cạnh ít nhất cần được xóa đi khỏi ~G~ để ~P~ trở thành đường đi duy nhất từ đỉnh ~1~ tới đỉnh ~n~. Nếu không có cách nào xóa cạnh để thỏa mãn điều kiện trên, hãy in ra ~-1~.
~^\dagger~ Một đường đi ~P~ từ đỉnh ~1~ tới đỉnh ~n~ là một danh sách các chỉ số cạnh ~p_1, p_2, \dots, p_k~ sao cho:
~u_{p_1} = 1~.
~v_{p_i} = u_{p_{i + 1}}~ với mọi ~1 \le i < k~.
~v_{p_k} = n~.
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên chứa số lượng test case ~t~ (~1 \leq t \leq 10\,000~). Mô tả của mỗi test case như sau.
Dòng đầu tiên chứa ba số nguyên ~n~, ~m~, và ~k~ (~2 \le n \le 10^5~, ~1 \le m, k \le 10^5~) — số lượng đỉnh và cạnh của đồ thị ~G~, và số lượng cạnh trong đường đi ~P~.
Dòng thứ ~i~ trong ~m~ dòng tiếp theo chứa hai số nguyên ~u_i~ và ~v_i~ (~1 \le u_i, v_i \le n~, ~u_i \neq v_i~) — cạnh thứ ~i~ của đồ thị ~G~.
Dòng tiếp theo chứa ~k~ số nguyên ~p_1, p_2, \ldots, p_k~ (~1 \le p_i \le m~) biểu diễn một đường đi từ ~1~ tới ~n~. Dữ liệu đảm bảo rằng các chỉ số cạnh này tạo thành một đường đi từ đỉnh ~1~ tới đỉnh ~n~.
Đảm bảo rằng tổng của ~n~, tổng của ~m~, và tổng của ~k~ qua tất cả các test case không vượt quá ~10^5~.
Output
Với mỗi test case, in ra một số nguyên là số lượng cạnh ít nhất cần được xóa đi để ~P~ trở thành đường đi duy nhất từ đỉnh ~1~ tới đỉnh ~n~. Nếu không có cách nào xóa cạnh để thỏa mãn điều kiện trên, hãy in ra ~-1~.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~1000~ | ~n = m~, ~G~ liên thông yếu ~^\ddagger~ |
| 2 | ~500~ | Tổng của ~n~ không vượt quá ~1000~, ~k = 1~, ~u_i \neq n~ và ~v_i \neq 1~ với mọi ~1 \le i \le m~ |
| 3 | ~1250~ | Tổng của ~n~ không vượt quá ~1000~ |
| 4 | ~500~ | Không có ràng buộc gì thêm |
| Tổng | ~3250~ |
~^\ddagger~ Một đồ thị có hướng được gọi là liên thông yếu nếu sau khi thay thế tất cả các cạnh có hướng thành cạnh vô hướng, đồ thị trở nên liên thông.
Sample Input 1
3
5 5 4
1 3
3 2
4 3
2 4
4 5
1 2 4 5
5 6 3
1 2
2 3
3 5
3 1
4 3
1 4
6 5 3
5 5 5
1 2
2 3
3 4
4 2
2 5
1 2 3 4 5
Sample Output 1
1
2
-1
Notes
Đối với test case đầu tiên, hình dưới sau đây minh họa đồ thị ~G~, với đường đi ~P~ được tô đỏ. Ta cần xóa cạnh ~4 \to 3~, vì có đường đi ~1 \to 3 \to 2 \to 4 \to 3 \to 2 \to 4 \to 5~ sử dụng cạnh này và đi từ ~1~ đến ~5~.

Minh họa cho test case đầu tiên.
Đối với test case thứ hai, hình dưới sau đây minh họa đồ thị ~G~, với đường đi ~P~ được tô đỏ. Ta cần xóa cạnh ~2 \to 3~ và cạnh ~3 \to 1~.
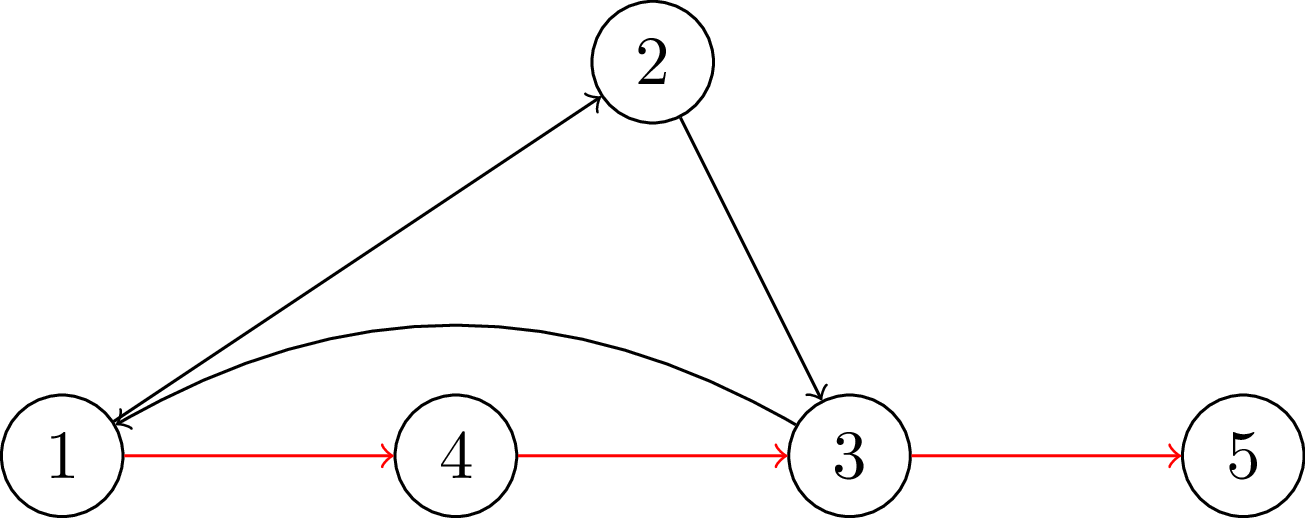
Minh họa cho test case thứ hai.
Bình luận