Mạng Truyền Thông 2
Xem dạng PDFMột công ty nọ có ~n~ văn phòng được đánh số từ ~1~ đến ~n~. Công ty này muốn lắp đặt một vài đường dây liên lạc hai chiều giữa các văn phòng, sao cho giữa mọi cặp văn phòng ~i~, ~j~ (~i \neq j~) tồn tại ít nhất một đường liên lạc giữa chúng.
Có ~k~ nhà mạng cung cấp tổng cộng ~m~ đường dây liên lạc, trong đó đường dây thứ ~i~ kết nối văn phòng ~u_i~ và văn phòng ~v_i~, được vận hành bởi nhà mạng ~c_i~ và mất chi phí ~p_i~ đồng~^\dagger~ để lắp đặt (lưu ý mỗi cặp văn phòng có thể có đường dây của nhiều nhà mạng).
Ngoài ra, để tăng tính cạnh tranh, cả ~k~ nhà mạng đều đang tổ chức chương trình tri ân khách hàng; cụ thể, nếu tổng chi phí lắp đặt mà công ty trả cho nhà mạng thứ ~j~ vượt quá ~s_j~ đồng, nhà mạng ~j~ sẽ giảm giá ~50\%~ cho phần chi phí chênh lệch, nghĩa là công ty sẽ chỉ phải trả ~x_j - \frac{\max(0, x_j - s_j)}{2}~ đồng, với ~x_j~ là tổng chi phí trước khi áp dụng khuyến mãi.
Hãy tìm cách dựng mạng lưới liên lạc sao cho tổng chi phí là nhỏ nhất có thể. Vì ta có thể chứng minh là tổng chi phí nhỏ nhất nhân ~2~ là một số nguyên, bạn cần in ra tổng chi phí nhỏ nhất nhân ~2~.
~^\dagger~ ~1~ triệu đồng tương đương khoảng ~420~ Krone Na Uy.
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên chứa số lượng test case ~t~ (~1 \leq t \leq 100~). Mô tả của mỗi test case như sau.
Dòng đầu tiên gồm ba số nguyên dương ~n~, ~m~, ~k~ (~2 \leq n \leq 1000~, ~n - 1 \leq m \leq 5 \cdot 10^5~, ~1 \leq k \leq 10~) — số lượng văn phòng của công ty, số lượng đường dây có thể lắp đặt, và số lượng nhà mạng.
Dòng thứ ~i~ trong ~m~ dòng tiếp theo gồm bốn số nguyên dương ~u_i~, ~v_i~, ~c_i~, ~p_i~ (~1 \leq u_i, v_i \leq n~, ~u_i \neq v_i~, ~1 \leq c_i \leq k~, ~1 \leq p_i \leq 10^9~), mô tả đường dây thứ ~i~.
Dòng cuối cùng gồm ~k~ số nguyên dương ~s_1, s_2, \cdots, s_k~ (~1 \leq s_i \leq 10^9~), mô tả chi tiết chương trình tri ân khách hàng của ~k~ nhà mạng.
Mỗi test case đảm bảo tồn tại ít nhất một cách dựng mạng lưới liên lạc kết nối tất cả ~n~ văn phòng.
Đảm bảo rằng tổng của ~n~ qua tất cả các test case không vượt quá ~1000~, và tổng của ~m~ không vượt quá ~5 \cdot 10^5~.
Output
Với mỗi test case, in ra một số nguyên là tổng chi phí nhỏ nhất để dựng mạng lưới liên lạc nhân ~2~.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~500~ | ~k = 1~ |
| 2 | ~1000~ | ~k \le 2~ |
| 3 | ~1000~ | Không có ràng buộc gì thêm |
| Tổng | ~2500~ |
Sample Input 1
4
3 4 2
1 2 1 3
2 3 1 5
1 2 2 4
1 3 2 4
5 6
3 4 2
1 2 1 3
2 3 1 5
1 2 2 4
1 3 2 4
1 1
5 7 3
1 5 3 100
1 2 1 5
4 5 1 5
1 3 2 7
2 3 3 10
1 2 2 4
4 5 2 4
5 20 100
2 3 3
1 2 1 5
1 2 2 6
1 2 3 7
6 2 2
Sample Output 1
13
9
225
8
Notes
Với test case thứ nhất, hình minh họa bên dưới biểu diễn các đường dây kết nối được phép lắp đặt, với các đường dây màu đỏ thuộc nhà mạng thứ ~1~ và đường dây màu xanh thuộc nhà mạng thứ ~2~. Với ~s = [5, 6]~, ta nên lắp đặt các đường dây được tô đậm. Tổng chi phí trước khuyến mãi phải chi cho nhà mạng thứ ~1~ và thứ ~2~ lần lượt là ~[8, 0]~, nên tổng chi phí sau khuyến mãi là ~\left(8 - \frac{\max(0, 8 - 5)}{2}\right) + \left(0 - \frac{\max(0, 0 - 6)}{2}\right) = \frac{13}{2}~.
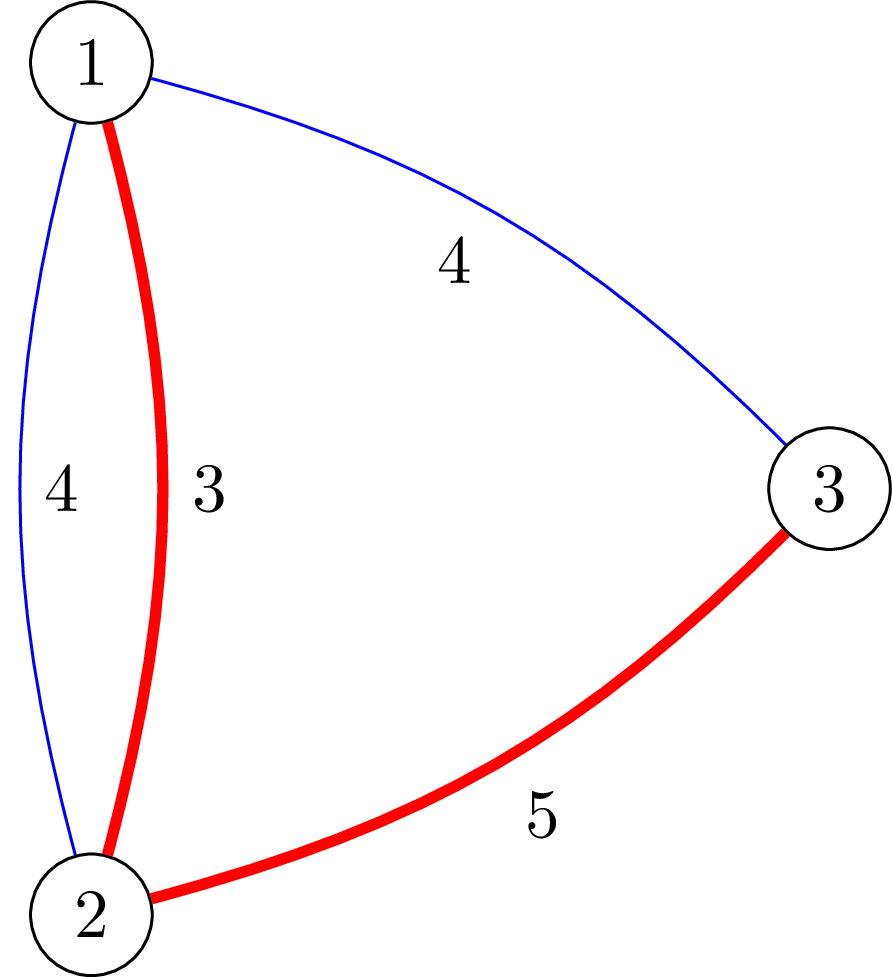
Hình minh họa ví dụ thứ nhất.
Với test case thứ hai, các đường dây được phép lắp đặt tương tự như test case thứ nhất. Với ~s = [1, 1]~, ta nên lắp đặt các đường dây được tô đậm. Tổng chi phí trước khuyến mãi phải chi cho nhà mạng thứ ~1~ và thứ ~2~ lần lượt là ~[3, 4]~, nên tổng chi phí sau khuyến mãi là ~\left(3 - \frac{\max(0, 3 - 1)}{2}\right) + \left(4 - \frac{\max(0, 4 - 1)}{2}\right) = \frac{9}{2}~.
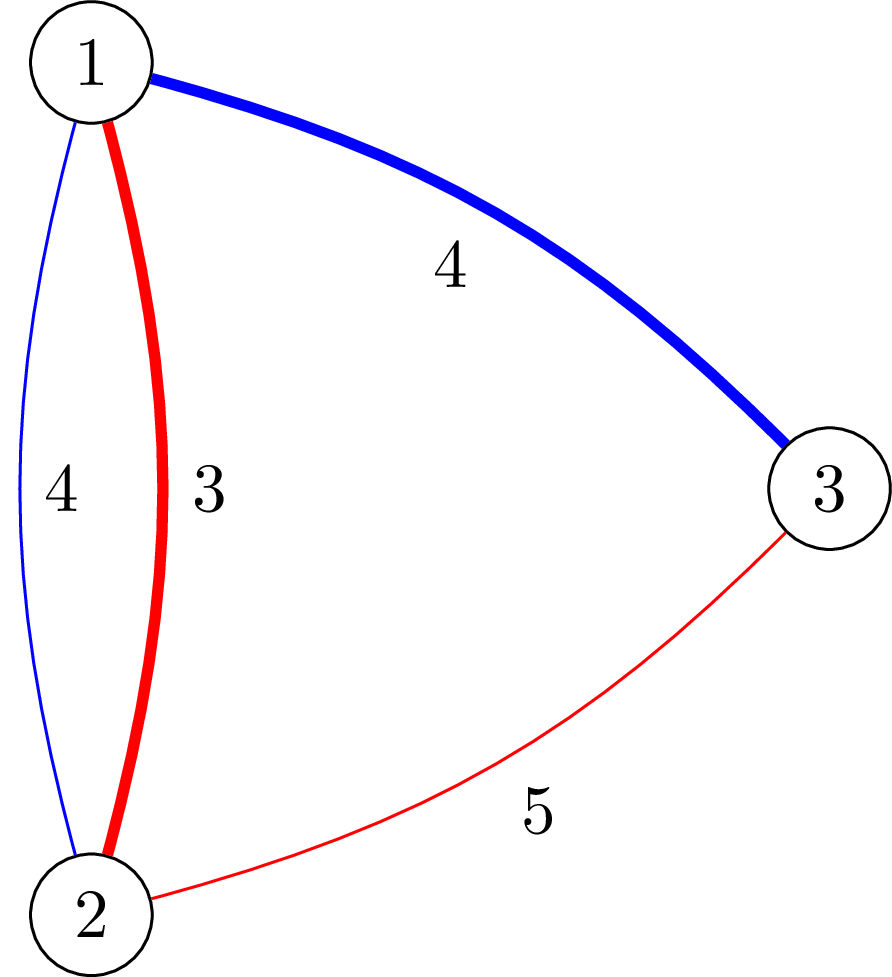
Hình minh họa ví dụ thứ hai.
Bình luận
Bài khó quá