[Mirror] VNOI Cup 2022 - Final
Điểm: 100
To read the problem statement in English, choose the language using the flag on the navigation bar.
Cho một đồ thị vô hướng gồm ~n~ đỉnh và ~m~ cạnh, trong đó không có cạnh nào nối một đỉnh với chính nó, và cũng không có hai đỉnh nào được nối trực tiếp với nhau bởi nhiều cạnh. Ban đầu, các đỉnh trong đồ thị đều có màu trắng. Hãy tô màu một số đỉnh trong đồ thị bởi màu xanh thỏa mãn ~q~ điều kiện, điều kiện thứ ~i~ yêu cầu rằng khoảng cách từ đỉnh ~c_i~ đến đỉnh màu xanh gần nó nhất (tính cả chính nó) là ~d_i~.
Input
Dòng đầu tiên gồm ba số nguyên ~n~, ~m~ và ~q~ (~1 \le q \le n \le 5 \times 10^5~, ~0 \le m \le 5 \times 10^5~) lần lượt là số đỉnh trong đồ thị, số cạnh của đồ thị, và số lượng điều kiện.
Mỗi dòng trong ~m~ dòng tiếp theo chứa ba số nguyên ~u~ và ~v~ (~1 \le u, v \le n~, ~u \ne v~) thể hiện có cạnh nối hai đỉnh ~u~ và ~v~ trong đồ thị. Dữ liệu đảm bảo không có hai đỉnh nào được nối với nhau trực tiếp bởi nhiều cạnh.
Dòng thứ ~i~ trong ~q~ dòng tiếp theo chứa hai số nguyên ~c_i~ và ~d_i~ (~1 \le c_i \le n~, ~0 \le d_i < n~) là mô tả điều kiện thứ ~i~: khoảng cách từ đỉnh ~c_i~ đến đỉnh màu xanh gần nó nhất là ~d_i~. Không có đỉnh nào xuất hiện trong hai điều kiện khác nhau.
Output
Nếu không tồn tại cách tô màu thỏa mãn yêu cầu đề bài, hãy in ra một
dòng duy nhất chứa từ NO.
Ngược lại, dòng đầu tiên hãy in ra YES. Dòng thứ hai hãy in ra số ~k~
là số đỉnh được chọn để tô màu xanh. Dòng tiếp theo hãy in ra ~k~ số
nguyên ~p_1, p_2, \ldots, p_k~ (~p_i \ne p_j~ với ~i \ne j~) là các đỉnh
nên được tô màu xanh.
Nếu có nhiều cách tô thỏa mãn đề bài, hãy in ra cách tô màu bất kì.
Scoring
Subtask 1, tương ứng với ~10~ điểm, có ~n \le 16~.
Subtask 2, tương ứng với ~20~ điểm, có ~n \le 5000~.
Subtask 3, tương ứng với ~70~ điểm, không có giới hạn gì thêm.
Tổng cộng bài toán có ~100~ điểm.
Sample Input 1
7 8 3
1 2
2 3
3 4
4 1
4 5
5 6
6 4
5 7
7 2
4 1
2 1
Sample Output 1
YES
2
1 6
Sample Input 2
4 3 1
1 2
2 3
3 1
4 0
Sample Output 2
YES
2
1 4
Sample Input 3
3 3 1
1 2
2 3
3 1
1 2
Sample Output 3
NO
Notes
Ở ví dụ thứ nhất, ta có thể tô hai đỉnh ~1~ và ~6~ xanh:
Từ đỉnh ~7~, có thể đi đến đỉnh màu xanh gần nhất là đỉnh ~6~ theo đường đi ~7 \rightarrow 5 \rightarrow 6~.
Từ đỉnh ~4~, có thể đi đến đỉnh màu xanh gần nhất là đỉnh ~1~ theo đường đi ~4 \rightarrow 1~.
Từ đỉnh ~2~, có thể đi đến đỉnh màu xanh gần nhất là đỉnh ~1~ theo đường đi ~2 \rightarrow 1~.
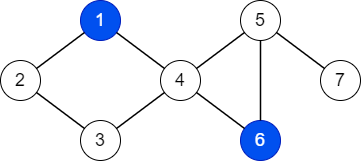
Hình vẽ minh họa ví dụ thứ nhất.
Một cách tô màu khác là tô hai đỉnh ~3~ và ~6~ xanh.
Ở ví dụ thứ hai, ta có thể tô đỉnh ~4~ xanh. Các đỉnh còn lại có thể tô hoặc không tô màu xanh tùy ý.
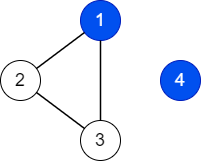
Hình vẽ minh họa ví dụ thứ hai.
Ở ví dụ thứ ba, khoảng cách từ đỉnh ~1~ đến hai đỉnh còn lại đều là ~1~, nên không có cách nào để tô màu thỏa mãn điều kiện khoảng cách từ đỉnh ~1~ đến đỉnh xanh gần nhất là ~2~.
Điểm: 100
To read the problem statement in English, choose the language using the flag on the navigation bar.
Cho số ~n~. Hãy tìm dãy số nguyên dương ~a~ thỏa mãn các điều kiện sau:
Các phần tử của dãy ~a~ không quá ~n + 1~.
Không có hai phần tử trong dãy ~a~ có cùng giá trị.
Với mỗi ~x~ từ ~2~ đến ~n~, tồn tại cặp chỉ số ~(i, j)~ sao cho ~i \neq j~ và ~a_i \equiv a_j \pmod x~.
Số phần tử của dãy ~a~ là nhỏ nhất có thể.
Input
Gồm một số nguyên ~n~ (~2 \le n \le 10^5~).
Output
Dòng đầu tiên in ra ~k~ – độ dài dãy ~a~ tìm được.
Dòng thứ hai in ra ~k~ số nguyên ~a_1, a_2, \ldots, a_k~ thỏa mãn điều kiện đề bài.
Nếu có nhiều đáp án thỏa mãn điều kiện, hãy in ra đáp án bất kì.
Scoring
Subtask 1, tương ứng với ~10~ số điểm, có ~n \le 16~.
Subtask 2, tương ứng với ~90~ số điểm, không có giới hạn gì thêm
Tổng cộng bài toán có ~100~ điểm.
Sample Input 1
5
Sample Output 1
4
1 3 5 6
Notes
Có thể thấy dãy ~[1, 3, 5, 6]~ thỏa mãn điều kiện thứ nhất và thứ hai của đề bài. Dãy này cũng thỏa mãn điều kiện thứ ba:
Cặp phần tử mang giá trị ~1~ và ~5~ có cùng số dư là ~1~ khi chia cho ~x = 2~.
Cặp phần tử mang giá trị ~3~ và ~6~ cùng chia hết cho ~x = 3~.
Cặp phần tử mang giá trị ~1~ và ~5~ có cùng số dư là ~1~ khi chia cho ~x = 4~.
Cặp phần tử mang giá trị ~1~ và ~6~ có cùng số dư là ~1~ khi chia cho ~x = 5~.
Có thể chỉ ra rằng, với ~n = 5~ thì không có dãy ~a~ nào có ít hơn ~4~ phần tử thỏa yêu cầu đề bài.
Điểm: 100
To read the problem statement in English, choose the language using the flag on the navigation bar.
Lục bát là một thể thơ của Việt Nam, đúng như tên gọi, một cặp câu thơ cơ bản gồm một câu sáu âm tiết và một câu tám âm tiết, phối vần với nhau. Một bài thơ lục bát gồm nhiều cặp câu tạo thành và không hạn chế số câu. Thơ lục bát là thể loại thơ rất phổ biến do có luật thơ rất đơn giản nhưng rất dễ gợi nhớ.
Cụ thể hơn, trong bài toán này ta định nghĩa một bài thơ lục bát như sau.
Bài thơ lục bát sẽ có ~2 \cdot n~ câu thơ, trong đó có ~n~ câu lục vần (câu có 6 tiếng) và ~n~ câu bát vần (câu có 8 tiếng).
Các câu lục vần sẽ là các câu ở vị trí đầu tiên, thứ 3, thứ 5, ~\ldots~
Các câu bát vần sẽ là các câu ở vị trí thứ 2, thứ 4, thứ 6, ~\ldots~
Câu trước cần có tiếng cuối vần với tiếng thứ sáu của câu tiếp theo.
Hai từ được gọi là vần nhau nếu như multiset của các nguyên âm (tức các kí tự
a,e,i,ovàu) của hai từ đó là như nhau.
Cho ~n~ câu thơ lục vần và ~n~ câu thơ bát vần, hãy tìm cách sắp xếp lại các câu thơ này để các câu thơ trở thành một bài thơ lục bát.
Input
Dòng đầu tiên chứa số nguyên ~n~ (~1 \le n \le 10^5~) là số lượng câu lục vần và bát vần trong bài thơ.
Dòng thứ ~i~ trong ~n~ dòng tiếp theo chứa ~6~ từ của một câu thơ lục vần.
Dòng thứ ~i~ trong ~n~ dòng tiếp theo chứa ~8~ từ của một câu thơ bát vần.
Mỗi từ trong input chỉ bao gồm các kí tự tiếng anh in thường. Tổng độ dài của tất cả các từ không quá ~10^7~.
Output
Nếu như ~2n~ câu thơ đã cho không thể tọa ra thành một bài thơ lục bát
bằng cách sắp xếp lại các câu, hãy in ra một dòng duy nhất chứa NO.
Ngược lại, dòng đầu tiên hãy in ra YES. Tiếp đó hãy in ~2n~ dòng tiếp
theo thể hiện bài thơ đã thu được.
Scoring
Subtask 1, tương ứng với ~10~ điểm, có ~n \le 6~.
Subtask 2, tương ứng với ~90~ điểm, không có ràng buộc gì thêm.
Tổng cộng bài toán sẽ có ~100~ điểm.
Sample Input 1
2
nhi vang bong trang la xanh
trong dam gi dep bang sen
gan bun ma chang hoi tanh mui bun
la xanh bong trang lai chen nhi vang
Sample Output 1
YES
trong dam gi dep bang sen
la xanh bong trang lai chen nhi vang
nhi vang bong trang la xanh
gan bun ma chang hoi tanh mui bun
Sample Input 2
3
trai qua mot cuoc be dau
la gi bi sac tu phong
tram nam trong coi nguoi ta
troi xanh quen thoi ma hong danh ghen
chu tai chu menh kheo la ghet nhau
nhung dieu trong thay ma dau don long
Sample Output 2
YES
tram nam trong coi nguoi ta
chu tai chu menh kheo la ghet nhau
trai qua mot cuoc be dau
nhung dieu trong thay ma dau don long
la gi bi sac tu phong
troi xanh quen thoi ma hong danh ghen
Điểm: 150
To read the problem statement in English, choose the language using the flag on the navigation bar.
Đây là một bài toán interactive.
Tài và anh trai rất thích chơi trò chơi tạo số. Đầu tiên hai anh em sẽ chọn ra một số nguyên tố ~n~. Sau đó cả hai sẽ chuẩn bị ra ~n~ mảnh giấy và xếp chúng ngay ngắn theo một hàng ngang. Các tờ giấy được đánh số từ ~1~ đến ~n~ từ phải qua trái.
Trò chơi sẽ diễn ra như sau. Hai anh em sẽ luân phiên chơi, với Tài là người đi trước. Người chơi khi đến lượt đi của mình sẽ chọn ra một mảnh giấy chưa được viết lên, và viết lên đó một chữ số từ ~0~ đến ~9~ theo ý của mình. Trò chơi sẽ kết thúc khi tất cả các mảnh giấy đã được viết lên.
Tài đang học đến số học, và rất thích sự chia hết. Vì vậy Tài muốn rằng sau khi trò chơi kết thúc, con số thu được khi đọc các mảnh giấy từ trái qua phải sẽ là một số chia hết cho ~n~. Tất nhiên để trò chơi thêm phần vui vẻ, mang tính chất đối kháng, anh của Tài sẽ cố gắng điền các số sao cho số được tạo ra sẽ không chia hết cho ~n~.
Cho biết số ~n~ mà hai anh em đã chọn, hãy giúp Tài chiến thắng trò chơi
này bằng cách tạo ra một số chia hết cho ~n~. Lưu ý rằng số tạo thành
sau khi trò chơi kết thúc có thể bắt đầu bằng chữ số 0.
Interaction
Trong bài toán này bạn sẽ chơi trò chơi với vai Tài và chương trình của ban tổ chức sẽ chơi với vai của anh trai Tài.
Đầu tiên chương trình của ban tổ chức sẽ in ra một số ~t~ (~1 \le t \le 10~) là số trận hai anh em sẽ chơi. Mỗi trận chơi sẽ được diễn ra như sau.
Đầu tiên chương trình của ban tổ chức sẽ in ra một số ~n~ (~1 \le n \le 100\,000~, ~n~ là số nguyên tố) là số mà hai anh em đã cùng chọn với nhau.
Tiếp đó bạn cùng chương trình của ban tổ chức sẽ thực hiện ~n~ lần luân phiên nhau in ra hai số nguyên ~p~ và ~d~ (~1 \le p \le n~, ~0 \le d \le 9~) thể hiện người chơi khi đến lượt sẽ điền chữ số ~d~ vào mảnh giấy thứ ~p~ từ phải sang trái.
Sau ~n~ lần cùng nhau tương tác, chương trình của ban tổ chức sẽ in ra một số ~x~. Trong trường hợp số được tạo ra là số chia hết cho ~n~, ban tổ chức sẽ in ra ~x = 1~. Khi đó bạn có thể tiếp tục thao tác với trận tiếp theo (nếu có). Trường hợp mà số được tạo thành không chia hết cho ~n~, chương trình của ban tổ chức sẽ in ra ~x = 0~ và không in thêm dữ liệu nào nữa. Trong trường hợp này, bạn cần dừng chương trình của mình để nhận được verdict Wrong answer (đáp án sai), nếu không bạn sẽ nhận được kết quả bất kì.
Sau mỗi một lần in đáp án, hãy nhớ flush đầu ra chuẩn, nếu không bạn có thể nhận verdict Time Limit Exceeded. Để làm điều này, bạn có thể sử dụng:
fflush(stdout)hoặccout.flush()trong C++;System.out.flush()trong Java;flush(output)trong Pascal;stdout.flush()trong Python;- xem tài liệu chuẩn đối với các ngôn ngữ khác.
Scoring
Subtask 1, tương ứng với ~30~ điểm, có ~n < 10~.
Subtask 2, tương ứng với ~120~ điểm, không có ràng buộc gì thêm.
Tổng cộng bài toán có ~150~ điểm.
Sample 1
| Chương trình của BTC | Chương trình của thí sinh |
|---|---|
2 2 2 5 1 3 2 3 1 |
1 8 1 5 3 7 |
Notes
Ở ví dụ trên có ~t = 2~ trận.
Ở trận đầu tiên có ~n = 2~, Tài đi trước và chọn điền vào mảnh giấy thứ nhất từ phải sang trái chữ số ~8~. Chữ số trên các mảnh giấy lúc này là:
_8
Sau đó, chương trình của ban tổ chức chọn điền chữ số ~5~ vào mảnh giấy thứ hai từ phải sang trái. Chữ số trên các mảnh giấy lúc này là:
58
Số tạo ra khi đọc các mảnh giấy là ~58~, đây là một số chia hết cho ~2~ nên chương trình của ban tổ chức sẽ in ra ~x = 1~ và bắt đầu trận tiếp theo.
Ở trận thứ hai có ~n = 3~, Tài đi trước và chọn điền vào mảnh giấy thứ nhất từ phải sang trái chữ số ~5~. Chữ số trên các mảnh giấy lúc này là:
__5
Sau đó, chương trình của ban tổ chức chọn điền chữ số ~3~ vào mảnh giấy thứ hai từ phải sang trái. Chữ số trên các mảnh giấy lúc này là:
_35
Cuối cùng, Tài chọn điền chữ số ~7~ vào mảnh giấy thứ ba từ phải sang trái. Chữ số trên các mảnh giấy lúc này là:
735
Số tạo ra khi đọc các mảnh giấy là ~735~, đây là một số chia hết cho ~3~ nên chương trình của ban tổ chức sẽ in ra ~x = 1~ và kết thúc. Tài đã chiến thắng tất cả các trận.
Điểm: 150
To read the problem statement in English, choose the language using the flag on the navigation bar.
Lộc thích màu lam đậm, nên lần đầu tiên mà Lộc đăng kí tài khoản trên
một trang Online Judge giấu tên, Lộc đã quyết định sử dụng nickname
darkcyan. Buồn thay, nickname này đã được sử dụng. Vì nickname bị
trùng lặp, hệ thống có gợi ý Lộc sử dụng các nickname khác như
darkcyan_no1, darkcyan_pro và darkcyan_vip, tuy nhiên Lộc không
thích các nickname đó. Sau một hồi đắn đo suy nghĩ, nickname mà Lộc chọn
là darkkcyan, rất gần với nickname ban đầu, nhưng kí tự k được nhân
đôi lên. Và thật may mắn là nickname này chưa tồn tại! Nickname này đã
được Lộc sử dụng cho hệ thống này cũng như trên nhiều nền tảng khác
nhau.
Lộc nhận thấy rằng việc thay đổi nickname như thế thật là thú vị, và có thể áp dụng ý tưởng này để tạo ra một hệ thống gợi ý nickname hoàn toàn mới! Cụ thể, với một nickname được biểu diễn bởi xâu gồm ~k~ kí tự ~t_1 t_2 \ldots t_l~, hệ thống có thể biến đổi nickname sử dụng theo tác sau một số lần (có thể là 0 lần):
- Hệ thống chọn ra một vị trí ~i~ (~1 \le i \le l~) ngẫu nhiên. Các vị trí đều có xác suất được chọn là như nhau. Hệ thống sau đó sẽ chèn ~c~ kí tự ~t_i~ vào ngay sau vị trí ~i~. Các kí tự mới có chỉ số là ~i + 1, i + 2, \ldots, i + c - 1~ và các kí tự sau đó có chỉ số được tăng lên ~c~. Độ dài của nickname mới sẽ là ~l + c~.
Số lượng ~c~ các kí tự sẽ chèn thêm sẽ được hệ thống tính toán như sau:
Gán ~c \leftarrow 1~.
Hệ thống sẽ liên tục tung một đồng xu có xác suất sấp ngửa là 50/50. Trong khi đồng xu còn ngửa, hệ thống sẽ tăng ~c~ lên một.
Bước thứ hai có thể được lặp lại bởi hệ thống nhiều lần, tuy nhiên nếu ~c~ đã đạt đến giới hạn ~k~, hệ thống sẽ dừng tính toán giá trị ~c~ tại đây.
Cụ thể hơn, số ~c~ sẽ được tính toán bởi mã giả sau:
c = 1;
while c != k and coinToss() == head:
c = c + 1;
Ví dụ, với nickname darkcyan (với độ dài là ~8~) và giới hạn ~k = 3~.
Nickname
darkkcyansẽ có xác suất được tạo ra là ~\frac{1}{8} \cdot 50\% = \frac{1}{16}~ (xác suất chọn kí tựklà ~\frac{1}{8}~ và xác suất cho việc tung đồng xu ra mặt sấp là ~50\%~). Các nickname khác nhưddarkcyan,darrkcyanhaydarkcyanncũng có xác suất được tạo ra tương tự.Nickname
darkkkcyansẽ có xác suất được tạo ra là ~\frac{1}{8} \cdot 50\% \cdot 50\% = \frac{1}{32}~ (xác suất chọn kí tựklà ~\frac{1}{8}~ và xác suất cho việc tung đồng xu ra đầu tiên ra mặt ngửa là ~50\%~, và xác suất để tung đồng xu thứ hai ra mặtsấplà ~50\%~). Các nickname khác nhưdddarkcyan,darrrkcyanhaydarkcyannncũng có xác suất được tạo ra tương tự.Các nickname
darkkkkcyan,ddddarkkcyan,darrrrkcyanhaydarkcyannnnsẽ có xác suất được tạo ra không phải là ~\frac{1}{64}~, mà cũng là ~\frac{1}{32}~, do lúc này số lượng kí tự ~c~ được thêm vào đã đạt đến ~k = 3~.
Lưu ý: với ~k = -1~, ta có thể coi số lần tung đồng xu là không giới hạn.
Thiết kế của hệ thống này có sử dụng phương pháp ngẫu nhiên để sinh ra nickname mới. Lộc quyết định thiết kế như vậy để giảm thiểu chi phí cho việc kiểm tra nickname tồn tại trong quá trình tạo ra nickname mới, nhưng khả năng tạo ra một nickname ngắn gọn vẫn rất cao với số bước cần thực hiện được kì vọng là không quá lớn.
Lộc nghĩ rằng sẽ thật đáng tiếc nếu như không có hệ thống gợi ý nickname trùng lặp nào sử dụng ý tưởng này. Do đó Lộc quyết định áp dụng luôn hệ thống gợi ý nickname này cho mạng xã hội Virtual Network for Online Intercommunication (VNOI) mà mình đang tham gia phát triển. Hiện tại trên mạng xã hội VNOI đã có ~n~ người dùng, và người dùng thứ ~i~ có nickname là xâu kí tự ~S_i~. Lộc muốn biết rằng, với mỗi nickname ~S_i~, nếu nếu như có một người dùng mới khi đăng kí hệ thống sử dụng nickname trùng với nickname này, vậy giá trị kì vọng số thao tác thao tác biến đổi nickname này để tạo ra một nickname chưa được sử dụng trên VNOI là bao nhiêu. Vì Lộc vẫn đang bận phát triển thành phần khác của hệ thống, nên Lộc muốn nhờ các bạn giải quyết bài toán này.
Cho danh sách nickname của ~n~ người dùng trên hệ thống, yêu cầu với mỗi nickname ~S_i~, cần in ra giá trị kì vọng số thao tác biến đổi để biến đổi nickname ~S_i~ thành một nickname mới chưa tồn tại trên hệ thống. Để đảm bảo các kết quả được so sánh một cách chính xác, hãy in ra đáp án modulo ~10^9 + 7~.
Cụ thể hơn, đặt ~M = 10^9 + 7~. Ta có thể chỉ ra rằng đáp án có thể biểu diễn bởi một phân số tối giản ~\frac{p}{q}~, với ~p~ và ~q~ nguyên tố cùng nhau và ~q \not \equiv 0 \pmod{M}~. Hãy in ra số nguyên ~p \cdot q^{-1} \bmod M~. Nói cách khác, hãy in ra số nguyên ~x~ thỏa mãn ~0 \le x < M~ và ~x \cdot q \equiv p \pmod{M}~.
Input
Dòng đầu tiên chứa hai số nguyên ~n~ và ~k~ (~1 \le n \le 10^5~, ~1 \le k \le 10^9~ hoặc ~k = -1~) là số lượng người dùng mạng xã hội VNOI và giới hạn số kí tự có thể được thêm vào trong 1 phép biến đổi. Nếu ~k = -1~, số lượng kí tự được thêm vào là không giới hạn.
Dòng thứ ~i~ trong ~n~ dòng tiếp theo chứa xâu ~S_i~ (~1 \le |S_i| \le 10^5~, ~S_i~ chỉ chứa các kí tự tiếng Anh in thường) là nickname của người dùng thứ ~i~ trên hệ thống.
Dữ liệu đảm bảo tổng độ dài của tất cả các nickname trên hệ thống không quá ~10^5~ và không tồn tại hai nickname nào giống nhau.
Output
In ra ~n~ dòng. Dòng thứ ~i~ là giá trị kì vọng số lượng thao tác biến đổi để biến đổi nickname ~S_i~ thành một nickname mới chưa tồn tại trên hệ thống, modulo ~10^9 + 7~.
Scoring
Subtask 1, tương ứng với ~45~ điểm, có ~1 \le k \le 10~.
Subtask 2, tương ứng với ~105~ điểm, không có ràng buộc gì thêm.
Tổng cộng bài toán có ~150~ điểm.
Sample Input 1
3 2
aaa
aa
a
Sample Output 1
1
500000005
250000004
Sample Input 2
2 -1
b
bbb
Sample Output 2
250000003
1
Sample Input 3
3 1
ab
aab
abb
Sample Output 3
2
1
1
Notes
Trong ví dụ đầu tiên, nickname aa cần kì vọng ~\frac{3}{2}~ thao tác
biến đổi. Do hai kí tự giống nhau, nên ta có thể bỏ qua đi xác suất chọn
kí tự trong xâu và tính toán dựa vào xác suất tung đồng xu:
Xác suất cho việc tạo ra xâu
aaalà ~50\%~ nếu như trong lần đầu tiên tung đồng xu ra kết quả sấp. Vì nickname này đã trùng nên ta cần thêm 1 lần biến đổi nữa. Không quan trọng kết quả cuối cùng, trong trường hợp này ta cần ~2~ thao tác biến đổi.Xác suất cho việc tạo ra xâu
aaaalà ~50\%~ do giới hạn số lượng kí tự có thể thêm vào là ~k = 2~. Vì không có nickname nào khác trùng với nickname này, nên ta cần ~1~ thao tác biến đổi.
Do đó kì vọng số lượng biến đổi sẽ là ~50\% \cdot (2 + 1) = \frac{3}{2}~.
Nickname a trong ví dụ đầu tiên cần kì vọng ~\frac{9}{4}~ thao tác
biến đổi.
Trong ví dụ thứ hai không có giới hạn số lượng kí tự có thể thêm vào.
Nickname b khi đó có khả năng biến đổi sau:
tạo ra nickname
bbbvới xác suất ~50\% \cdot 50\% = 25\%~. Trong trường hợp này, không kể kết quả cuối cùng, ta cần thêm một thao tác biến đổi nữa vì đây là nickname đã tồn tại, do đó trường hợp này ta cần ~2~ thao tác biến đổi.tạo ra nickname khác
bbbvới xác suất là ~1 - 25\% = 75\%~. Trong trường hợp này ta thu được một nickname mới, do đó ta cần ~1~ thao tác biến đổi.
Do đó kì vọng số lượng biến đổi sẽ là ~25\% \cdot 2 + 75\% \cdot 1 = \frac{5}{4}~ thao tác biến đổi.
Điểm: 200
To read the problem statement in English, choose the language using the flag on the navigation bar.
Đây là một bài toán interactive.
~\textit{ngfam}~ có một chiếc máy tính lượng tử với cấu trúc vô cùng đặc biệt gồm ~n~ cổng lượng tử đánh số từ ~1~ tới ~n~. Cổng lượng tử thứ ~i~ mang một tham số đặc trưng ~c_i~ ~(0 \leq c_i \leq 100)~.
Để sử dụng chiếc máy tính, người sử dụng cần nhập vào máy một số nguyên không âm ~a~. Cùng thời điểm, chiếc máy sẽ khởi tạo biến số ~x = 1~. Sau đó, lần lượt các cổng lượng tử từ ~1~ tới ~n~ sẽ được kích hoạt. Khi kích hoạt cổng lượng tử thứ ~i~, chiếc máy sẽ thay đổi giá trị của ~x~ theo một trong hai khả năng sau:
~x \leftarrow (x \times a) \bmod 998\,244\,353~
~x \leftarrow (x \times c_i) \bmod 998\,244\,353~
trong đó ~a \bmod b~ là số dư của ~a~ khi chia cho ~b~.
Hai khả năng biến đổi của mỗi cổng lượng tử có xác suất xảy ra là như nhau, và tổng thể có ~2^n~ khả năng biến đổi giá trị ~x~ trong toàn bộ quá trình kích hoạt ~n~ cổng lượng tử. Tuy nhiên đây là chiếc máy tính lượng tử, nên thay vì trả về trả về một giá trị cụ thể của số ~x~, chiếc máy tính sẽ trả về giá trị chồng lập của ~x~, tương đương với giá trị kì vọng của ~x~ trong tất cả mọi khả năng xảy ra.
Là người dựng ra chiếc máy, ~\textit{ngfam}~ đã cài đặt các tham số trị ~c_i~ của ~n~ cổng lượng tử theo ý của mình, nhưng ~\textit{ngfam}~ sẽ không tiết lộ các tham số này cho bạn. Đổi lại, ~\textit{ngfam}~ sẽ cho bạn sử dụng chiếc máy tính lượng tử ~2 \cdot n~ lần: bạn có thể chọn các tham số ~a~ mà bạn muốn, và máy tính sẽ trả lại giá trị kì vọng của ~x~ tương ứng. Sau khi sử dụng xong, ~\textit{ngfam}~ muốn chắc chắn rằng bạn đã hiểu nguyên lý hoạt động của chiếc máy tính dựa vào các câu mà bạn đã hỏi, nên bạn cần trả lời ~\textit{ngfam}~ ~q~ câu hỏi tương tự tới từ ~\textit{ngfam}~ mà không được phép sử dụng chiếc máy tính đó nữa.
Lưu ý là kết quả của giá trị chồng lập có thể không phải là số nguyên, máy tính lượng tử cũng sẽ trả về kết quả modulo ~998\,244\,353~.
Cụ thể, gọi ~M = 998\,244\,353~ và giá trị chồng lập là ~\frac{p}{q}~, với ~p~ và ~q~ là hai số nguyên tố cùng nhau và ~q \not \equiv 0 \pmod{M}~, vậy máy tính sẽ trả về số ~p \cdot q^{-1} \bmod M~. Nói cách khác, số mà máy tính trả về là số ~r~ thỏa mãn ~0 \le r < M~ và ~r \cdot q \equiv p \pmod{M}~.
Input
Dòng đầu tiên chứa hai số nguyên ~n~ và ~q~ (~1\le n \le 50\,000~, ~1 \le q \le 50~) lần lượt là số cổng lượng tử của chiếc máy tính, và số câu hỏi mà bạn cần trả lời sau quá trình sử dụng máy tính.
Phần tiếp theo bạn cần tương tác với chương trình của ban tổ chức.
Interaction
Sau đó bạn có quyền đặt tối đa ~2 \cdot n~ câu hỏi, mỗi câu hỏi cần được in ra theo định dạng ? a (~0 \leq a < 998\,244\,353~). Sau đó chương trình của ban tổ chức sẽ in ra một số nguyên dương là giá trị chồng lập của ~x~ sau khi sử dụng máy tính với tham số ~a~.
Khi bạn đã sử dụng xong, bạn cần in ra dâu ! thể hiện là bạn muốn kết thúc quá trình hỏi.
Tiếp đó, bạn cần lần lượt trả lời ~q~ câu hỏi từ ~\textit{ngfam}~. Với mỗi câu hỏi, chương trình của ban tổ chức sẽ in ra một số nguyên ~a~ (~0 \le a \le 998\,244\,353~). Bạn cần tính toán và in ra giá trị chống lập ~x~ mà máy tính lượng tử sẽ trả về khi được sử dụng với tham số ~a~. Bạn cần trả lời các câu hỏi lần lượt, tức bạn phải trả lời câu hỏi hiện tại trước khi có thể đọc được câu hỏi tiếp theo.
Sau mỗi một lần in đáp án, hãy nhớ flush đầu ra chuẩn, nếu không bạn có thể nhận verdict Time Limit Exceeded. Để làm điều này, bạn có thể sử dụng:
fflush(stdout)hoặccout.flush()trong C++;System.out.flush()trong Java;flush(output)trong Pascal;stdout.flush()trong Python;- xem tài liệu chuẩn đối với các ngôn ngữ khác.
Scoring
Subtask 1, tương ứng với ~20~ điểm, có ~n \le 50~ và ~1 \le c_i \le 2~.
Subtask 2, tương ứng với ~60~ điểm, có ~n \le 50~.
Subtask 3, tương ứng với ~120~ điểm, không có ràng buộc gì thêm.
Tổng cộng bài toán có ~200~ điểm.
Sample 1
| Chương trình của BTC | Chương trình của thí sinh |
|---|---|
2 2 5 499122184 1 2 |
? 3 ? 4 ! 499122178 3 |
Sample 2
| Chương trình của BTC | Chương trình của thí sinh |
|---|---|
1 5 3 1 2 3 4 5 |
? 1 ! 3 499122180 4 499122181 5 |
Notes
Ở ví dụ thứ nhất, các cổng lượng tử có giá trị đặc biệt là ~c_1 = 1~ và ~c_2 = 2~. Hai câu đã được hỏi là ~a = 3~ và ~a = 4~. Với ~a = 3~, các khả năng sau có thể xảy ra:
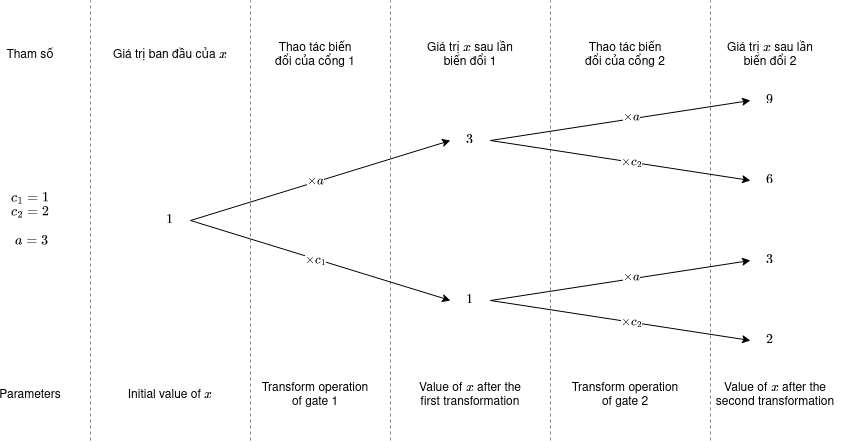
Như vậy với ~a = 3~, các giá trị ~x~ có khả năng thu về là ~[9, 6, 3, 2]~, và giá trị kì vọng của ~x~ trong các khả năng sẽ là ~\frac{9 + 6 + 3 + 2} {2^2} = \frac{20} {4} = 5~
Với ~a = 4~, các giá trị có thể thu được sẽ là:
~1 \times a \times a = 1 \times 4 \times 4 = 16~
~1 \times a \times c_2 = 1 \times 4 \times 2 = 8~
~1 \times c_1 \times a = 1 \times 1 \times 4 = 4~
~1 \times c_1 \times c_2 = 1 \times 1 \times 2 = 2~
Giá trị chồng lập của ~x~ khi sử dụng máy tính lượng tử này với ~a = 4~ sẽ là ~\frac{16 + 8 + 4 + 2} {2^2} = \frac{30}{4} = \frac{15}{2}~. Số mà máy tính lượng tử in ra là ~499122184~ bởi vì ~499122184 \times 2 \equiv 15 \bmod (998\,244\,353)~.
Với ~a = 1~, các khả năng thu được giá trị ~x~ là ~[1, 2, 1, 2]~, và với ~a = 2~, các khả năng thu được giá trị ~x~ là ~[4, 4, 2, 2]~.
Ở ví dụ thứ hai, giá trị đặc biệt của cổng lượng tử duy nhất là ~c_1 = 5~.
Điểm: 200
To read the problem statement in English, choose the language using the flag on the navigation bar.
Lower envelope (bao hình dưới) của tập ~n~ đường thẳng, trong đó đường thẳng thứ ~i~ có phương trình ~y_i = a_i \cdot x + b_i~, có đồ thị được biểu diễn bởi phương trình ~y = \min_{i = 1}^n\{ a_i \cdot x + b_i \}~.
Ta gọi đỉnh của lower envelope là điểm nằm trên lower envelope và đồng thời cũng là giao của hai đường thẳng khác nhau trong các đường thẳng đã cho. Giả sử lower envelope có ~k~ đỉnh ~p_1, p_2, \ldots, p_k~, với đỉnh ~p_i~ có hoành độ nhỏ hơn đỉnh ~p_{i + 1}~ (~1 \le i < k~). Ta gọi chu vi của lower envelope là tổng khoảng cách hai đỉnh liên tiếp của lower envelope, tức tổng ~p_1 p_2 + p_2 p_3 + \ldots p_{k - 1} p_k~. Nếu như lower envelope có ít hơn hai đỉnh, ta coi chu vi của lower envelope bằng ~0~.
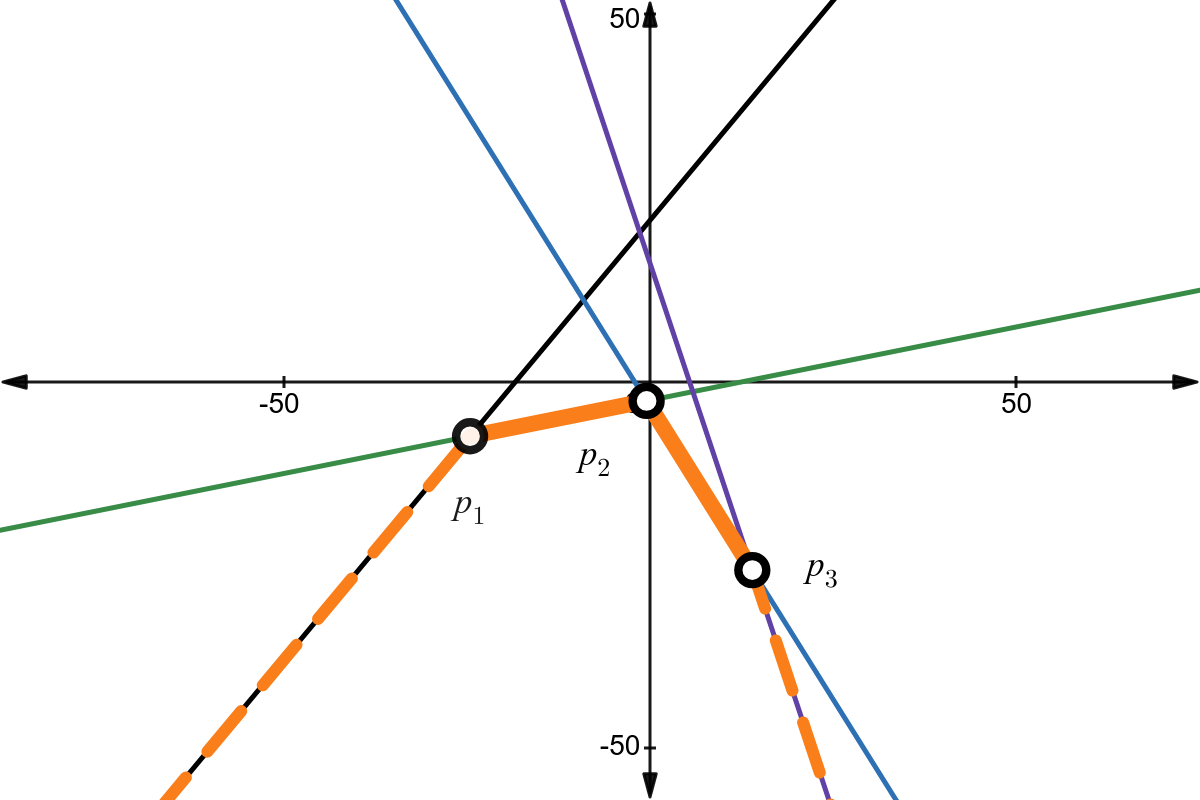
Lower envelope của 4 đường thẳng trong hình là đường màu đường màu cam. Lower envelope có 3 đỉnh ~p_1~, ~p_2~ và ~p_3~. Chu vi của Lower envelope thể hiện bởi đường màu cam liền mạch.
Cho ~n~ đường thẳng. Với mỗi đường thẳng, hãy tìm chu vi của lower envelope tạo bởi ~n - 1~ đường thẳng còn lại.
Input
Dòng đầu tiên gồm số nguyên ~n~ (~2 \le n \le 100\, 000~) là số đường thẳng.
Dòng thứ ~i~ trong ~n~ dòng tiếp theo chứa hai số nguyên ~a_i~ và ~b_i~ (~|a_i|, |b_i| \le 10^9~) là tham số của đường thẳng thứ ~i~.
Dữ liệu đảm bảo rằng không có hai đường thẳng nào trùng nhau.
Output
Hãy in ra ~n~ dòng. Dòng thứ ~i~ chứa chu vi của lower envelope của tập ~n - 1~ đường thẳng nếu như ta bỏ đi đường thẳng thứ ~i~.
Đáp án của bạn được cho là chính xác nếu như sai số tuyệt đối hoặc sai số tương đối đáp án không quá ~10^{-6}~.
Cụ thể hơn, gọi đáp án của bạn là ~a~ và đáp án của ban tổ chức là ~b~. Đáp án của bạn sẽ được cho là chính xác nếu như ~\frac{|a - b|}{\max{(1, |b|)}} \le 10^{-6}~.
Scoring
Subtask 1, tương ứng với ~30~ điểm, có ~n \le 100~.
Subtask 2, tương ứng với ~40~ điểm, có ~n \le 1000~.
Subtask 3, tương ứng với ~130~ điểm, không có ràng buộc gì thêm.
Tổng cộng bài toán có ~200~ điểm.
Sample Input 1
4
0 0
0 1
1 0
-1 3
Sample Output 1
1.0
3.0
0
0
Sample Input 2
5
4 21
-3 -13
1 -3
3 15
1 -1
Sample Output 2
9.1923881554
0.0000000000
6.1282587703
7.7781745931
7.7781745931
Notes
Dưới đây là hình minh họa cho ví dụ 1.
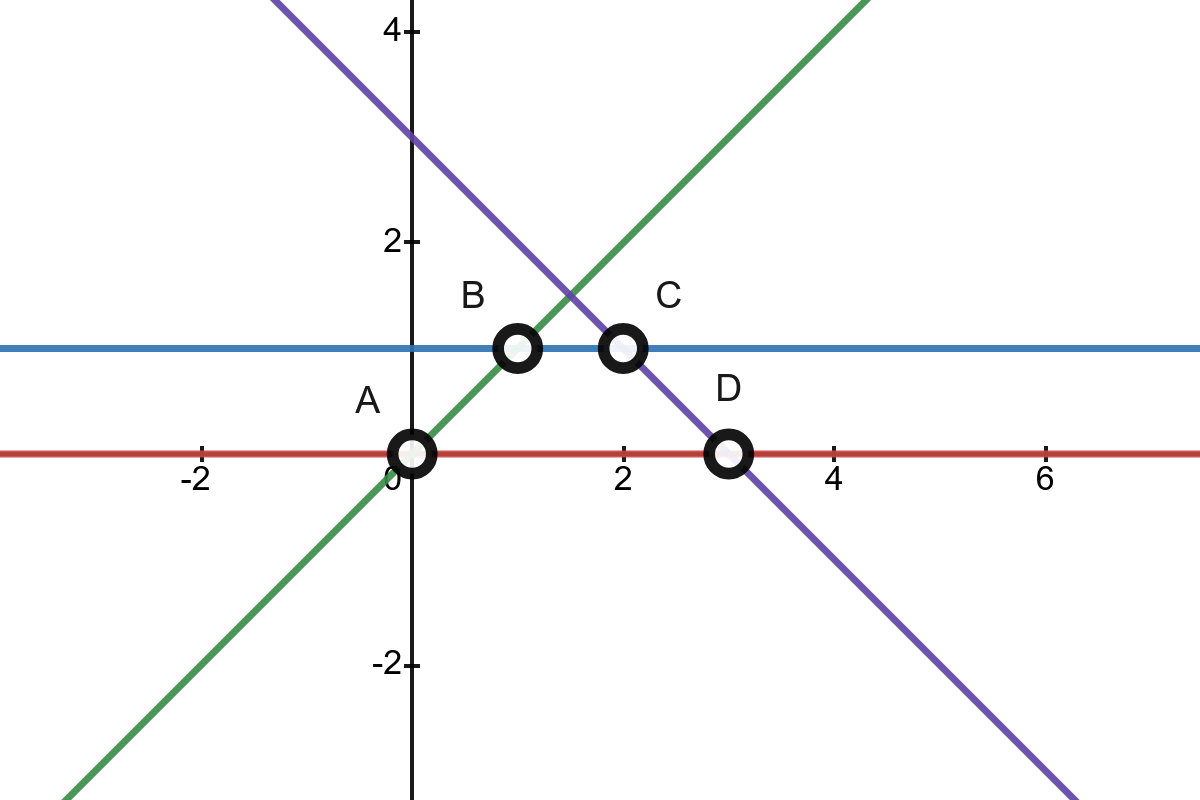
Đường thẳng đầu tiên có phương trình ~y = 0x + 0~ với màu đỏ. Bỏ đi đường thẳng này, lower envelope sẽ có đỉnh ~B~ và ~C~.
Đường thẳng thứ hai có phương trình ~y = 0x + 1~ với màu xanh dương. Bỏ đi đường thẳng này, lower envelope sẽ có đỉnh ~A~ và ~D~.
Đường thẳng thứ ba có phương trình ~y = x~ với màu xanh lá. Bỏ đi đường thẳng này, lower envelope sẽ có đỉnh ~D~.
Đường thẳng cuối cùng có phương trình ~y = -x + 3~ với màu tím. Bỏ đi đường thẳng này, lower envelope sẽ có đỉnh ~A~.