To read the problem statement in English, choose the language using the flag on the navigation bar.

Đây là một bài toán interactive.

~\textit{ngfam}~ có một chiếc máy tính lượng tử với cấu trúc vô cùng đặc biệt gồm ~n~ cổng lượng tử đánh số từ ~1~ tới ~n~. Cổng lượng tử thứ ~i~ mang một tham số đặc trưng ~c_i~ ~(0 \leq c_i \leq 100)~.

Để sử dụng chiếc máy tính, người sử dụng cần nhập vào máy một số nguyên không âm ~a~. Cùng thời điểm, chiếc máy sẽ khởi tạo biến số ~x = 1~. Sau đó, lần lượt các cổng lượng tử từ ~1~ tới ~n~ sẽ được kích hoạt. Khi kích hoạt cổng lượng tử thứ ~i~, chiếc máy sẽ thay đổi giá trị của ~x~ theo một trong hai khả năng sau:

• ~x \leftarrow (x \times a) \bmod 998\,244\,353~

• ~x \leftarrow (x \times c_i) \bmod 998\,244\,353~

trong đó ~a \bmod b~ là số dư của ~a~ khi chia cho ~b~.

Hai khả năng biến đổi của mỗi cổng lượng tử có xác suất xảy ra là như nhau, và tổng thể có ~2^n~ khả năng biến đổi giá trị ~x~ trong toàn bộ quá trình kích hoạt ~n~ cổng lượng tử. Tuy nhiên đây là chiếc máy tính lượng tử, nên thay vì trả về trả về một giá trị cụ thể của số ~x~, chiếc máy tính sẽ trả về giá trị chồng lập của ~x~, tương đương với giá trị kì vọng của ~x~ trong tất cả mọi khả năng xảy ra.

Là người dựng ra chiếc máy, ~\textit{ngfam}~ đã cài đặt các tham số trị ~c_i~ của ~n~ cổng lượng tử theo ý của mình, nhưng ~\textit{ngfam}~ sẽ không tiết lộ các tham số này cho bạn. Đổi lại, ~\textit{ngfam}~ sẽ cho bạn sử dụng chiếc máy tính lượng tử ~2 \cdot n~ lần: bạn có thể chọn các tham số ~a~ mà bạn muốn, và máy tính sẽ trả lại giá trị kì vọng của ~x~ tương ứng. Sau khi sử dụng xong, ~\textit{ngfam}~ muốn chắc chắn rằng bạn đã hiểu nguyên lý hoạt động của chiếc máy tính dựa vào các câu mà bạn đã hỏi, nên bạn cần trả lời ~\textit{ngfam}~ ~q~ câu hỏi tương tự tới từ ~\textit{ngfam}~ mà không được phép sử dụng chiếc máy tính đó nữa.

Lưu ý là kết quả của giá trị chồng lập có thể không phải là số nguyên, máy tính lượng tử cũng sẽ trả về kết quả modulo ~998\,244\,353~.

Cụ thể, gọi ~M = 998\,244\,353~ và giá trị chồng lập là ~\frac{p}{q}~, với ~p~ và ~q~ là hai số nguyên tố cùng nhau và ~q \not \equiv 0 \pmod{M}~, vậy máy tính sẽ trả về số ~p \cdot q^{-1} \bmod M~. Nói cách khác, số mà máy tính trả về là số ~r~ thỏa mãn ~0 \le r < M~ và ~r \cdot q \equiv p \pmod{M}~.

Input

Dòng đầu tiên chứa hai số nguyên ~n~ và ~q~ (~1\le n \le 50\,000~, ~1 \le q \le 50~) lần lượt là số cổng lượng tử của chiếc máy tính, và số câu hỏi mà bạn cần trả lời sau quá trình sử dụng máy tính.

Phần tiếp theo bạn cần tương tác với chương trình của ban tổ chức.

Interaction

Sau đó bạn có quyền đặt tối đa ~2 \cdot n~ câu hỏi, mỗi câu hỏi cần được in ra theo định dạng ? a (~0 \leq a < 998\,244\,353~). Sau đó chương trình của ban tổ chức sẽ in ra một số nguyên dương là giá trị chồng lập của ~x~ sau khi sử dụng máy tính với tham số ~a~.

Khi bạn đã sử dụng xong, bạn cần in ra dâu ! thể hiện là bạn muốn kết thúc quá trình hỏi.

Tiếp đó, bạn cần lần lượt trả lời ~q~ câu hỏi từ ~\textit{ngfam}~. Với mỗi câu hỏi, chương trình của ban tổ chức sẽ in ra một số nguyên ~a~ (~0 \le a \le 998\,244\,353~). Bạn cần tính toán và in ra giá trị chống lập ~x~ mà máy tính lượng tử sẽ trả về khi được sử dụng với tham số ~a~. Bạn cần trả lời các câu hỏi lần lượt, tức bạn phải trả lời câu hỏi hiện tại trước khi có thể đọc được câu hỏi tiếp theo.

Sau mỗi một lần in đáp án, hãy nhớ flush đầu ra chuẩn, nếu không bạn có thể nhận verdict Time Limit Exceeded. Để làm điều này, bạn có thể sử dụng:

• fflush(stdout) hoặc cout.flush() trong C++;
• System.out.flush() trong Java;
• flush(output) trong Pascal;
• stdout.flush() trong Python;
• xem tài liệu chuẩn đối với các ngôn ngữ khác.

Scoring

• Subtask 1, tương ứng với ~20~ điểm, có ~n \le 50~ và ~1 \le c_i \le 2~.

• Subtask 2, tương ứng với ~60~ điểm, có ~n \le 50~.

• Subtask 3, tương ứng với ~120~ điểm, không có ràng buộc gì thêm.

Tổng cộng bài toán có ~200~ điểm.

Sample 1

2 2

5

499122184

1

2

  

? 3

? 4

!

499122178

3
  

Sample 2

1 5

3

1

2

3

4

5

  

? 1

!

3

499122180

4

499122181

5
  

Notes

Ở ví dụ thứ nhất, các cổng lượng tử có giá trị đặc biệt là ~c_1 = 1~ và ~c_2 = 2~. Hai câu đã được hỏi là ~a = 3~ và ~a = 4~. Với ~a = 3~, các khả năng sau có thể xảy ra:

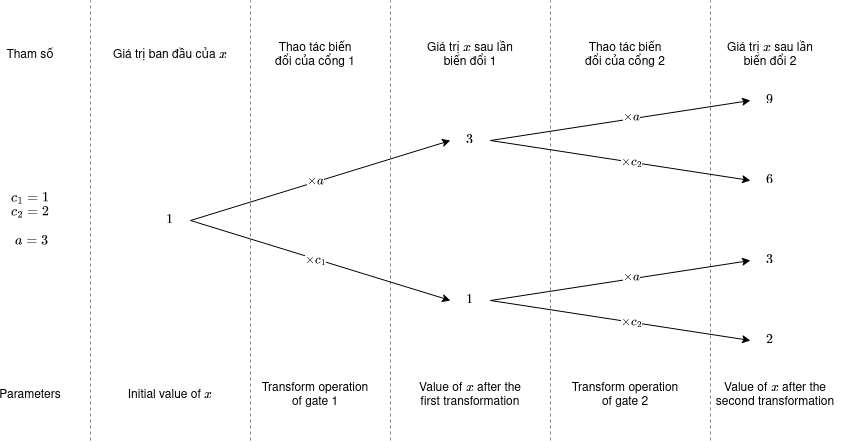
Như vậy với ~a = 3~, các giá trị ~x~ có khả năng thu về là ~[9, 6, 3, 2]~, và giá trị kì vọng của ~x~ trong các khả năng sẽ là ~\frac{9 + 6 + 3 + 2} {2^2} = \frac{20} {4} = 5~

Với ~a = 4~, các giá trị có thể thu được sẽ là:

• ~1 \times a \times a = 1 \times 4 \times 4 = 16~

• ~1 \times a \times c_2 = 1 \times 4 \times 2 = 8~

• ~1 \times c_1 \times a = 1 \times 1 \times 4 = 4~

• ~1 \times c_1 \times c_2 = 1 \times 1 \times 2 = 2~

Giá trị chồng lập của ~x~ khi sử dụng máy tính lượng tử này với ~a = 4~ sẽ là ~\frac{16 + 8 + 4 + 2} {2^2} = \frac{30}{4} = \frac{15}{2}~. Số mà máy tính lượng tử in ra là ~499122184~ bởi vì ~499122184 \times 2 \equiv 15 \bmod (998\,244\,353)~.

Với ~a = 1~, các khả năng thu được giá trị ~x~ là ~[1, 2, 1, 2]~, và với ~a = 2~, các khả năng thu được giá trị ~x~ là ~[4, 4, 2, 2]~.

Ở ví dụ thứ hai, giá trị đặc biệt của cổng lượng tử duy nhất là ~c_1 = 5~.