To read the problem statement in English, choose the language using the flag on the navigation bar.

Lower envelope (bao hình dưới) của tập ~n~ đường thẳng, trong đó đường thẳng thứ ~i~ có phương trình ~y_i = a_i \cdot x + b_i~, có đồ thị được biểu diễn bởi phương trình ~y = \min_{i = 1}^n\{ a_i \cdot x + b_i \}~.

Ta gọi đỉnh của lower envelope là điểm nằm trên lower envelope và đồng thời cũng là giao của hai đường thẳng khác nhau trong các đường thẳng đã cho. Giả sử lower envelope có ~k~ đỉnh ~p_1, p_2, \ldots, p_k~, với đỉnh ~p_i~ có hoành độ nhỏ hơn đỉnh ~p_{i + 1}~ (~1 \le i < k~). Ta gọi chu vi của lower envelope là tổng khoảng cách hai đỉnh liên tiếp của lower envelope, tức tổng ~p_1 p_2 + p_2 p_3 + \ldots p_{k - 1} p_k~. Nếu như lower envelope có ít hơn hai đỉnh, ta coi chu vi của lower envelope bằng ~0~.

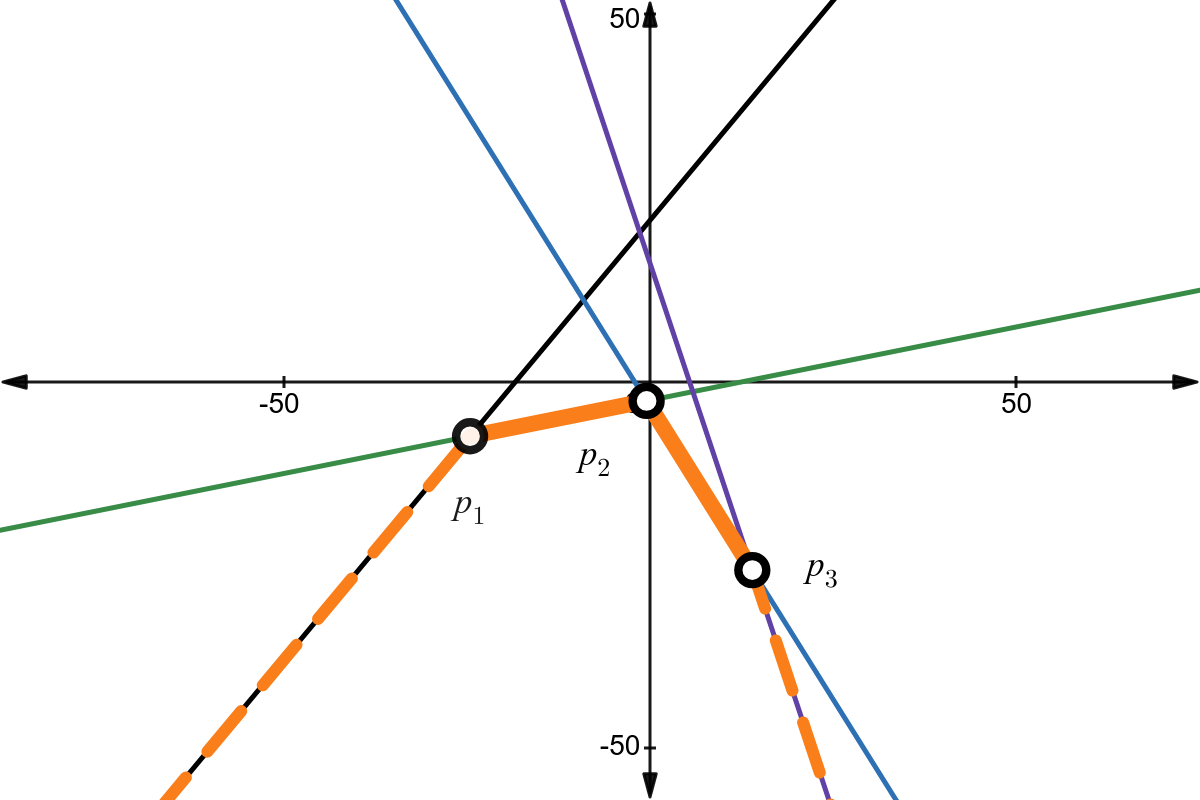
Lower envelope của 4 đường thẳng trong hình là đường màu đường màu cam. Lower envelope có 3 đỉnh ~p_1~, ~p_2~ và ~p_3~. Chu vi của Lower envelope thể hiện bởi đường màu cam liền mạch.

Cho ~n~ đường thẳng. Với mỗi đường thẳng, hãy tìm chu vi của lower envelope tạo bởi ~n - 1~ đường thẳng còn lại.

Input

Dòng đầu tiên gồm số nguyên ~n~ (~2 \le n \le 100\, 000~) là số đường thẳng.

Dòng thứ ~i~ trong ~n~ dòng tiếp theo chứa hai số nguyên ~a_i~ và ~b_i~ (~|a_i|, |b_i| \le 10^9~) là tham số của đường thẳng thứ ~i~.

Dữ liệu đảm bảo rằng không có hai đường thẳng nào trùng nhau.

Output

Hãy in ra ~n~ dòng. Dòng thứ ~i~ chứa chu vi của lower envelope của tập ~n - 1~ đường thẳng nếu như ta bỏ đi đường thẳng thứ ~i~.

Đáp án của bạn được cho là chính xác nếu như sai số tuyệt đối hoặc sai số tương đối đáp án không quá ~10^{-6}~.

Cụ thể hơn, gọi đáp án của bạn là ~a~ và đáp án của ban tổ chức là ~b~. Đáp án của bạn sẽ được cho là chính xác nếu như ~\frac{|a - b|}{\max{(1, |b|)}} \le 10^{-6}~.

Scoring

• Subtask 1, tương ứng với ~30~ điểm, có ~n \le 100~.

• Subtask 2, tương ứng với ~40~ điểm, có ~n \le 1000~.

• Subtask 3, tương ứng với ~130~ điểm, không có ràng buộc gì thêm.

Tổng cộng bài toán có ~200~ điểm.

Sample Input 1

4
0 0
0 1
1 0
-1 3

Sample Output 1

1.0
3.0
0
0

Sample Input 2

5
4 21
-3 -13
1 -3
3 15
1 -1

Sample Output 2

9.1923881554
0.0000000000
6.1282587703
7.7781745931
7.7781745931

Notes

Dưới đây là hình minh họa cho ví dụ 1.

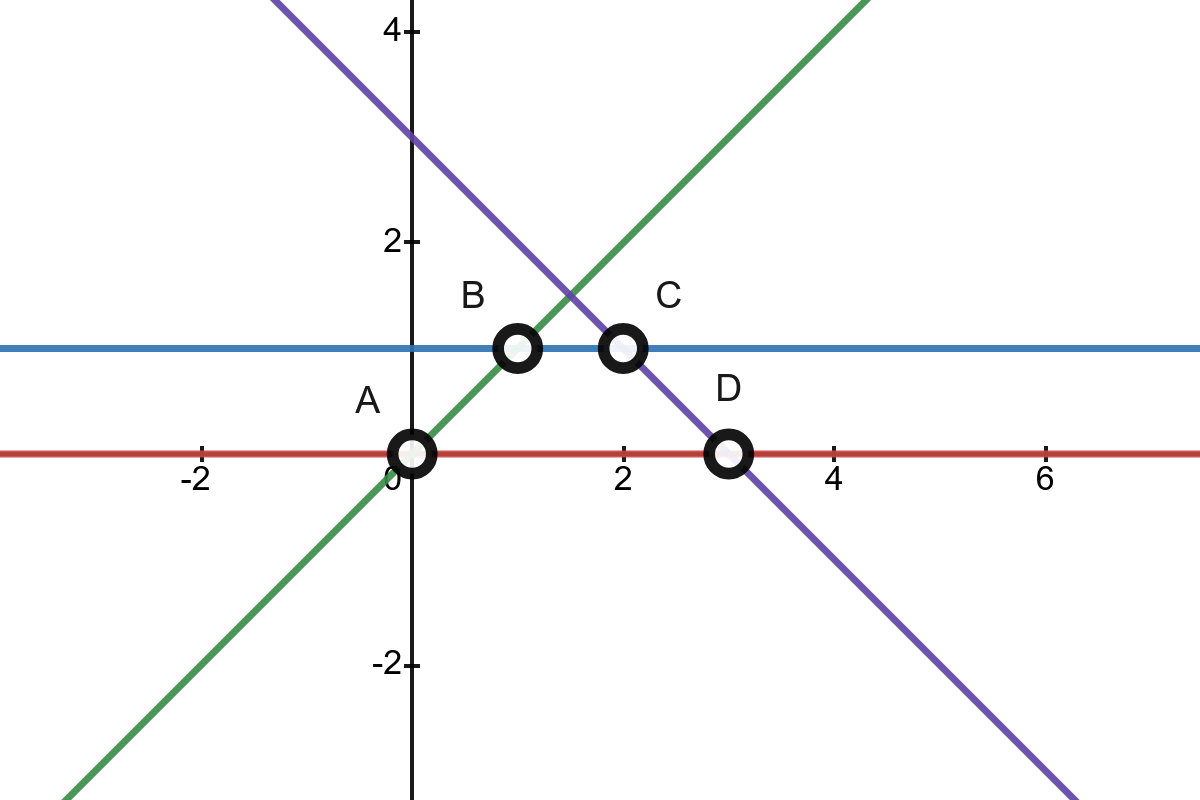
• Đường thẳng đầu tiên có phương trình ~y = 0x + 0~ với màu đỏ. Bỏ đi đường thẳng này, lower envelope sẽ có đỉnh ~B~ và ~C~.

• Đường thẳng thứ hai có phương trình ~y = 0x + 1~ với màu xanh dương. Bỏ đi đường thẳng này, lower envelope sẽ có đỉnh ~A~ và ~D~.

• Đường thẳng thứ ba có phương trình ~y = x~ với màu xanh lá. Bỏ đi đường thẳng này, lower envelope sẽ có đỉnh ~D~.

• Đường thẳng cuối cùng có phương trình ~y = -x + 3~ với màu tím. Bỏ đi đường thẳng này, lower envelope sẽ có đỉnh ~A~.