To read the problem statement in English, choose the language using the flag on the navigation bar.

Cho một đồ thị vô hướng gồm ~n~ đỉnh và ~m~ cạnh, trong đó không có cạnh nào nối một đỉnh với chính nó, và cũng không có hai đỉnh nào được nối trực tiếp với nhau bởi nhiều cạnh. Ban đầu, các đỉnh trong đồ thị đều có màu trắng. Hãy tô màu một số đỉnh trong đồ thị bởi màu xanh thỏa mãn ~q~ điều kiện, điều kiện thứ ~i~ yêu cầu rằng khoảng cách từ đỉnh ~c_i~ đến đỉnh màu xanh gần nó nhất (tính cả chính nó) là ~d_i~.

Input

Dòng đầu tiên gồm ba số nguyên ~n~, ~m~ và ~q~ (~1 \le q \le n \le 5 \times 10^5~, ~0 \le m \le 5 \times 10^5~) lần lượt là số đỉnh trong đồ thị, số cạnh của đồ thị, và số lượng điều kiện.

Mỗi dòng trong ~m~ dòng tiếp theo chứa ba số nguyên ~u~ và ~v~ (~1 \le u, v \le n~, ~u \ne v~) thể hiện có cạnh nối hai đỉnh ~u~ và ~v~ trong đồ thị. Dữ liệu đảm bảo không có hai đỉnh nào được nối với nhau trực tiếp bởi nhiều cạnh.

Dòng thứ ~i~ trong ~q~ dòng tiếp theo chứa hai số nguyên ~c_i~ và ~d_i~ (~1 \le c_i \le n~, ~0 \le d_i < n~) là mô tả điều kiện thứ ~i~: khoảng cách từ đỉnh ~c_i~ đến đỉnh màu xanh gần nó nhất là ~d_i~. Không có đỉnh nào xuất hiện trong hai điều kiện khác nhau.

Output

Nếu không tồn tại cách tô màu thỏa mãn yêu cầu đề bài, hãy in ra một dòng duy nhất chứa từ NO.

Ngược lại, dòng đầu tiên hãy in ra YES. Dòng thứ hai hãy in ra số ~k~ là số đỉnh được chọn để tô màu xanh. Dòng tiếp theo hãy in ra ~k~ số nguyên ~p_1, p_2, \ldots, p_k~ (~p_i \ne p_j~ với ~i \ne j~) là các đỉnh nên được tô màu xanh.

Nếu có nhiều cách tô thỏa mãn đề bài, hãy in ra cách tô màu bất kì.

Scoring

• Subtask 1, tương ứng với ~10~ điểm, có ~n \le 16~.

• Subtask 2, tương ứng với ~20~ điểm, có ~n \le 5000~.

• Subtask 3, tương ứng với ~70~ điểm, không có giới hạn gì thêm.

Tổng cộng bài toán có ~100~ điểm.

Sample Input 1

7 8 3
1 2
2 3
3 4
4 1
4 5
5 6
6 4
5 7
7 2
4 1
2 1

Sample Output 1

YES
2
1 6

Sample Input 2

4 3 1
1 2
2 3
3 1
4 0

Sample Output 2

YES
2
1 4

Sample Input 3

3 3 1
1 2
2 3
3 1
1 2

Sample Output 3

NO

Notes

Ở ví dụ thứ nhất, ta có thể tô hai đỉnh ~1~ và ~6~ xanh:

• Từ đỉnh ~7~, có thể đi đến đỉnh màu xanh gần nhất là đỉnh ~6~ theo đường đi ~7 \rightarrow 5 \rightarrow 6~.

• Từ đỉnh ~4~, có thể đi đến đỉnh màu xanh gần nhất là đỉnh ~1~ theo đường đi ~4 \rightarrow 1~.

• Từ đỉnh ~2~, có thể đi đến đỉnh màu xanh gần nhất là đỉnh ~1~ theo đường đi ~2 \rightarrow 1~.

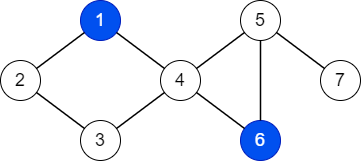
Hình vẽ minh họa ví dụ thứ nhất.

Một cách tô màu khác là tô hai đỉnh ~3~ và ~6~ xanh.

Ở ví dụ thứ hai, ta có thể tô đỉnh ~4~ xanh. Các đỉnh còn lại có thể tô hoặc không tô màu xanh tùy ý.

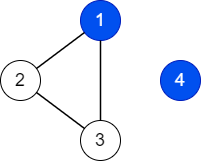
Hình vẽ minh họa ví dụ thứ hai.

Ở ví dụ thứ ba, khoảng cách từ đỉnh ~1~ đến hai đỉnh còn lại đều là ~1~, nên không có cách nào để tô màu thỏa mãn điều kiện khoảng cách từ đỉnh ~1~ đến đỉnh xanh gần nhất là ~2~.