Educational Matrix Exponentiation Contest
Điểm: 100
Limak có tâm trạng thất thường, và anh ấy luôn vui hoặc buồn. Tâm trạng anh ấy đổi với xác suất ~p~ mỗi giây. Nếu tâm trạng hiện tại của Limak đang vui, xác suất để anh ấy vui sau ~n~ giây là bao nhiêu?
Input
Gồm ~1~ dòng chứa ~1~ số nguyên ~n~ ~(1 \leq n \leq 10^{9})~ và một số thực ~p~ ~(0 \leq p \leq 1)~ có tối đa ~9~ chữ số sau dấu chấm phẩy.
Output
In ra 1 số duy nhất là xác suất để Limak vui sau ~n~ giây. Kết quả được tính là đúng nếu chênh lệch với đáp án không quá ~10^{-6}~.
Sample 1
Input
1 0.7
Output
0.3000000000
Giải thích
Có xác suất ~0.7~ là Limak sẽ thay đổi từ vui sang buồn. Còn lại, có xác suất ~0.3~ là anh ấy vẫn vui.
Sample 2
Input
2 0.1
Output
0.8200000000
Giải thích
Đáp án là ~0.1 \times 0.1+0.9 \times 0.9=0.82~. Đó là vì chúng ta muốn anh ấy đổi tâm trạng ~2~ lần hoăc không đổi lần nào hết.
Sample 3
Input
11 0.06
Output
0.6225404294
Điểm: 100
Limak, như bao người khác, lúc vui lúc buồn. Cảm xúc của anh ấy thay đổi (hoặc không thay đổi) khi anh ấy đọc một từ tiếng Anh với các chữ cái in hoa. Chữ S và D luôn làm anh ấy buồn, trong khi H làm anh ấy vui và các nguyên âm A,E,I,O,U làm đảo ngược cảm xúc của anh ấy (vui thành buồn hoặc ngược lại). Những chữ còn lại không làm thay đổi cảm xúc của anh ấy.
Hiện tại Limak đang vui. Trong tất cả ~26^n~ xâu với ~n~ chữ cái tiếng anh in hoa, đếm số xâu mà Limak sẽ vui sau khi đọc xâu đó. In ra đáp án modulo ~10^9+7~
Input
Một số nguyên dương ~n~ ~(1 \le n \le 10^{18})~.
Output
In ra đáp án modulo ~10^9+7~.
Sample 1
Input
1
Output
19
Giải thích
Có tất cả ~19~ xâu có độ dài ~n=1~ làm Limak cảm thấy vui là: B, C, F,G, H, J, K, L, M, N, P, Q, R, T, V, W, X, Y, Z.
Các xâu có nguyên âm và chữ S hoặc D sẽ làm Limak thấy buồn.
Sample 2
Input
2
Output
403
Giải thích
Với ~n=2~, có ~403~ xâu làm Limak thấy vui. Xâu AO là một ví dụ vì Limak sẽ thay đổi cảm xúc hai lần. Tương tự, xâu SO cũng được tính vì làm Limak buồn rồi sau đó vui trở lại với chữ O.
Sample 3
Input
11
Output
145418665
Điểm: 100
Hãy tìm phần dư của phép chia lấy dư số Fibonacci thứ ~n~ cho ~10^9+7~.
Số Fibonacci thứ ~n~ ~(F_n)~ được xác định bởi dãy truy hồi sau:
~F_0 = 0, F_1 = 1~
~F_n = F_{n-1} + F_{n-2}\ (\forall n \geq 2)~
Input
Gồm ~1~ dòng chứa số nguyên ~n~ ~(0 \leq n \leq 10^{18})~.
Output
Phần dư của phép chia ~F_n~ cho ~10^9 + 7~.
Sample 1
Input
3
Output
2
Sample 2
Input
6
Output
8
Sample 3
Input
50
Output
586268941
~F_{50} = 12586269025 \equiv 586268941~ ~(mod ~ ~10^9 + 7)~.
Note
Một vài số hạng đầu tiên của dãy số Fibonacci là ~(0,1,1,2,3,5,8,13,…)~.
Điểm: 100
Bạn được cho một đồ thị có hướng gồm ~n~ đỉnh và ~m~ cạnh, các đỉnh được đánh số từ ~1~ tới ~n~. Hãy đếm số đường đi có ~k~ bước (cạnh) và in ra kết quả theo modulo ~10^9 + 7~. Một đường đi có thể có ghé thăm các đỉnh và cạnh nhiều lần.
Input
Dòng đầu là ~3~ số nguyên ~n,\ m,\ k~ ~(1 \le n \le 100,\ 0 \le \ m \le n\cdot (n-1),\ 1 \le k \le 10^9)~ lần lượt là số đỉnh, số cạnh và số bước của đường đi.
~m~ dòng tiếp theo mô tả các cạnh của đồ thị. Dòng thứ ~i~ gồm ~2~ số nguyên ~a_i,\ b_i~ ~(1 \le a_i,\ b_i \le n, a_i \neq b_i)~ thể hiện đường đi từ đỉnh ~a_i~ tới đỉnh ~b_i~. Đồ thị đã cho đảm bảo không có khuyên và mỗi cạnh không xuất hiện quá một lần.
Output
In ra một dòng chứa số đường đi thoả mãn yêu cầu input theo modulo ~1000000007~.
Sample Input 1
3 4 2
1 2
2 3
3 1
2 1
Sample Output 1
5
Sample Input 2
5 10 11
2 3
4 2
2 1
2 4
1 5
5 2
3 2
3 1
3 4
1 2
Sample Output 2
21305
Giải thích
Ở ví dụ này, ta được cho đồ thị chứa ~3~ đỉnh và ~4~ cạnh như sau:
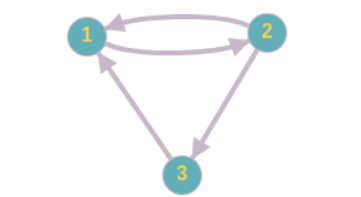
Có ~5~ đường đi với số bước ~k = 2~:
- ~1\rightarrow2\rightarrow1~
- ~1\rightarrow2\rightarrow3~
- ~2\rightarrow1\rightarrow2~
- ~2\rightarrow3\rightarrow1~
- ~3\rightarrow1\rightarrow2~
Điểm: 100
Một quân mã được đặt ở ô trái trên của bàn cờ kích thước ~8 \times 8~. Bạn được phép di chuyển quân mã đó tối đa ~k~ lần. Hãy đếm số đường đi có thể có với quân mã đó và in ra kết quả dưới dạng modulo cho ~2^{32}~.
Cụ thể hơn, một đường đi là một tập các ô ~(C_1, C_2,..., C_s)~ sao cho ~1 \le s \le k + 1~ và quân mã có thể đi từ ô ~C_i~ đến ô ~C_{i+1}~ với mọi ~i~.
(Một nước đi của quân mã trong bàn cờ vua có dạng ~1~ ô vuông theo chiều ngang và ~2~ ô vuông theo chiều dọc hoặc ~2~ ô vuông theo chiều ngang và ~1~ ô vuông theo chiều dọc)
Input
Số nguyên ~k~ ~(0 \le k \le 10^9)~
Output
In ra kết quả dưới dạng modulo cho ~2^{32} = 4294967296 ~
Sample 1
Input
1
Output
3
Sample 2
Input
2
Output
15
Sample 3
Input
6
Output
17231
Giải thích Sample 1
Quân mã có thể đứng nguyên ở ô ~(1, 1)~ hoặc có thể di chuyển tới các ô ~(2, 3)~ hoặc ~(3, 2)~. Vậy kết quả là ~3~.
Điểm: 100
Bạn được cho một đồ thị với ~n~ đỉnh (được đánh số từ ~1~ đến ~n~) và ~m~ cạnh có hướng và có trọng số. Tìm đường đi có ~k~ cạnh với tổng trọng số nhỏ nhất. Một đường đi có thể đi qua một đỉnh hay cạnh nhiều lần.
Nếu không tồn tại đường đi nào có ~k~ cạnh, in ra IMPOSSIBLE.
Input
Dòng đầu tiên gồm ~3~ số nguyên dương ~n~, ~m~ và ~k~ ~(1 \le n \le 100, 0 \le m \le n \cdot (n-1), 1 \le k \le 10^9)~
~m~ dòng tiếp theo miêu tả các cạnh. Trong đó dòng thứ ~i~ gồm 3 số ~a_i~, ~b_i~ và ~c_i~ ~(1 \le a_i,b_i \le n, a_i \neq b_i, -10^9 \le c_i \le 10^9)~, miêu tả một cạnh có hướng nối từ ~a_i~ đến ~b_i~ với trọng số ~c_i~. Đồ thị trong input đảm bảo không có cạnh trùng hoặc cạnh nối cùng một đỉnh với nhau.
Output
In ra đường đi đi qua ~k~ cạnh với tổng trọng số nhỏ nhất. Nếu không tồn tại đường đi nào đi qua ~k~ cạnh thì in ra IMPOSSIBLE.
Sample 1
Input
3 4 2
1 2 12
2 3 -5
3 1 20
2 1 -1
Output
7
Sample 2
Input
3 4 5
1 2 12
2 3 -5
3 1 20
2 1 -1
Output
17
Sample 3
Input
6 5 3
1 3 -50
2 4 -51
4 3 -52
3 6 -53
4 5 -54
Output
-156
Sample 4
Input
6 5 4
1 3 -50
2 4 -51
4 3 -52
3 6 -53
4 5 -54
Output
IMPOSSIBLE
Note
Hình vẽ dưới đây cho thấy đồ thị trong hai sample đầu tiên. Đường đi tối ưu lần lượt là ~1 \rightarrow 2 \rightarrow 3~ và ~2 \rightarrow 1 \rightarrow 2 \rightarrow 1 \rightarrow 2 \rightarrow 3~
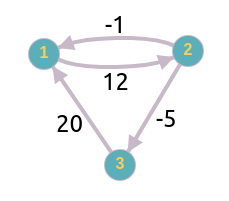
Điểm: 100
Dãy Fibonacci: ~F[i] = 1 \cdot F[i - 1] + 1 \cdot F[i - 2]~ là một dãy truy hồi tuyến tính (linear recurrence). Xét một công thức tổng quát hơn và cũng khó hơn: Chúng ta sẽ cho thêm biến ~i~ vào.
Cụ thể hơn, xét một dãy vô hạn đuợc định nghĩa bởi ~n~ phần tử đầu tiên: ~a_{0}, a_{1}, ..., a_{n - 1}~ và các hệ số ~c_{1}, c_{2}, ..., c_{n}, p, q, r~. Với mọi ~i \geq n~:
~a_{i} = (c_{1} \cdot a_{i - 1} + c_{2} \cdot a_{i - 2} + ... + c_{n} \cdot a_{i - n}) + p + i \cdot q + i^2 \cdot r~
Hãy tính ~a_{k} ~ ~mod~ ~10^9 + 7~ ~(1000000007)~.
Input
Dòng đầu chứa hai số nguyên duơng ~n~ ~(1 \leq n \leq 10)~ và ~k~ ~(1 \leq k \leq 10^{18})~.
Dòng thứ hai chứa ~n~ số nguyên ~a_{0}, a_{1}, ..., a_{n - 1}~ ~(0 \leq a_{i} < 10^9 + 7)~.
Dòng thứ ba chứa ~n~ số nguyên ~c_{1}, c_{2}, ..., c_{n}~ ~(0 \leq c_{i} < 10^9 + 7)~.
Dòng thứ tư chứa ~3~ số nguyên ~p, q, r~ ~(0 \leq p, q, r < 10^9 + 7)~.
Output
In ra một dòng chứa ~a_{k}~ ~mod~ ~10^9 + 7~.
Sample Input 1
2 2
0 30
2 1
2 1 1
Sample Output 1
68
Sample Input 2
1 3
5
1
2 3 4
Sample Output 2
85
Giải thích các test đề
Ở ví dụ thứ nhất, ta có ~a_{0} = 0, a_{1} = 30, a_{i} = (a_{i - 1} \cdot 2 + a_{i - 2}) + 2 + i + i^2~
Do đó ~a_{2} = 2 \cdot a_{1} + a_{0} + 2 + 2 + 2^2 = 2 \cdot 30 + 0 + 2 + 2 + 4 = 68~.
Ở ví dụ thứ hai, năm số đầu tiên của dãy là ~(5, 14, 38, 85, 163)~. Vì ~k = 3~, chúng ta in ra ~a_{3} = 85~.
Điểm: 100
Limak có hai trạng thái cảm xúc là hạnh phúc hoặc buồn bã. Tâm trạng của cậu ấy có thể thay đổi (hoặc không) mỗi khi cậu ấy đọc một chữ cái Tiếng Anh in hoa. Chữ cái S và D sẽ làm cậu ấy buồn bã, chữ cái H sẽ làm cậu ấy hạnh phúc, và các nguyên âm (A, E, I, O, U) sẽ đảo ngược tâm trạng của cậu ấy. Những chữ cái khác sẽ không ảnh hưởng gì cả. Limak hiện đang hạnh phúc và cậu ấy muốn mình vẫn hạnh phúc sau khi đọc một xâu kí tự.
Bạn được cho một xâu ~s~ với ~n~ kí tự. Một kí tự hợp lệ trong xâu là một dấu chẩm hỏi ? hoặc một chữ cái Tiếng Anh in hoa từ A đến Z. Nếu như xâu có ~x~ dấu chấm hỏi thì sẽ có tổng cộng ~26^x~ cách thay chúng thành các chữ cái từ A đến Z. Nhiệm vụ của bạn là đếm số cách thay các dấu chẩm hỏi sao cho Limak sẽ hạnh phúc sau khi đọc xong xâu mới (ban đầu Limak đang hạnh phúc).
Ngoài ra, còn có ~q~ phép cập nhật, mỗi phép có dạng ~(i, c)~ thể hiện thao tác thay đổi kí tự thứ ~i~ trong xâu ~s~ thành kí tự ~c~. Bạn cần in ra đáp án với xâu ~s~ ban đầu trước khi bắt đầu cập nhật và sau mỗi phép cập nhật, chia lấy dư cho ~10^9+7~.
Input
Dòng đầu tiên chứa hai số nguyên ~n~ và ~q~ ~(1 \leq n, q \leq 200\:000)~ - độ dài của xâu ~s~ và số lượng phép cập nhật.
Dòng thứ hai chứa xâu ~s~ ban đầu với ~n~ kí tự hợp lệ.
Mỗi dòng trong số ~q~ dòng tiếp theo chứa một số nguyên ~i~ ~(1 \leq i \leq n)~ và một kí tự hợp lệ ~c~. Mỗi phép cập nhật sẽ thay đổi kí tự thứ ~i~ của xâu ~s~ thành kí tự ~c~. Không có phép cập nhật nào sẽ đổi một kí tự thành chính kí tự đó.
Các kí tự trong xâu ~s~ được đánh số thứ tự từ ~1~ đến ~n~. Sau khi bạn thay đổi một kí tự, nó sẽ giữ nguyên cho tới khi nào nó bị thay đổi lần nữa (những phép cập nhật không phải là tạm thời).
Output
In ra ~q + 1~ dòng, mỗi dòng chứa đáp án ở thời điểm hiện tại, lấy số dư cho ~10^9 + 7~.
Sample Input
2 5
A?
2 O
1 H
1 ?
2 ?
2 H
Sample Output
6
1
0
7
403
26
Giải thích
Xâu ~s~ ban đầu là A? và sau các phép cập nhật lần lượt trở thành: AO, HO, ?O, ??, ?H.
Với xâu ban đầu A?, có tổng cộng ~6~ cách thay các dấu chấm hỏi để Limak cảm thấy hạnh phúc sau khi đọc hết xâu: AA, AE, AH, AI, AO, AU. Kí tự đầu tiên là một nguyên âm nên tâm trạng của Limak bị đảo ngược từ hạnh phúc sang buồn bã. Do đó, kí tự còn lại phải là một nguyên âm hoặc chữ cái H.
Điểm: 100
Bạn được cho một đồ thị có hướng gồm ~n~ đỉnh và ~m~ cạnh, các đỉnh được đánh số từ ~1~ tới ~n~ .
Đỉnh ~s~ được gọi là đến được đỉnh ~t~ trong ~k~ bước nếu như tồn tại một dãy ~k + 1~ đỉnh với đỉnh đầu tiên là đỉnh ~s~, đỉnh cuối cùng là đỉnh ~t~, sao cho luôn có đường đi trực tiếp giữa ~2~ đỉnh liên tiếp.
Bạn cần trả lời ~q~ truy vấn: cho ~3~ số ~s,\ k,\ t~, đếm số đường đi từ ~s~ tới ~t~ gồm đúng ~k~ bước. Một đường đi có thể đi qua một đỉnh hoặc một cạnh nhiều lần. Vì kết quả có thể rất lớn, hãy in ra số đường đi theo modulo ~10^9 + 7~.
Input
Dòng đầu là ~3~ số nguyên ~n,\ m,\ q~ ~(1 \le n,\ q \le 200, 0 \le m \le n \cdot (n - 1))~ lần lượt là số đỉnh, số cạnh và số truy vấn.
~m~ dòng tiếp theo mô tả các cạnh của đồ thị. Dòng thứ ~i~ gồm ~2~ số nguyên ~a_i,\ b_i~ ~(1 \le a_i,\ b_i \le n, a_i \neq b_i)~ thể hiện đường đi từ đỉnh ~a_i~ tới đỉnh ~b_i~. Đồ thị đã cho đảm bảo không có các cạnh lặp lại nhau.
~q~ dòng tiếp theo thể hiện các truy vấn. Mỗi dòng gồm ~3~ số nguyên ~s,\ t,\ k~ ~(1 \le s,\ t \le n,\ 1 \le k \le 10^9)~, lần lượt điểm xuất phát, điểm kết thúc và độ dài của một đường đi.
Output
Với mỗi truy vấn, in ra một dòng chứa đáp án theo modulo ~1000000007~, là câu trả lời cho truy vấn ấy.
Sample Input
3 4 4
1 2
2 3
3 1
2 1
1 2 6
3 3 5
1 3 1
3 2 54
Sample Output
2
1
0
922111
Giải thích
Ở ví dụ này, ta được cho đồ thị chứa ~3~ đỉnh và ~4~ cạnh như sau:

- ~1\rightarrow2\rightarrow3\rightarrow1\rightarrow2\rightarrow1\rightarrow2~
- ~1\rightarrow2\rightarrow1\rightarrow2\rightarrow3\rightarrow1\rightarrow2~