Bạn được cho một đồ thị có hướng gồm ~n~ đỉnh và ~m~ cạnh, các đỉnh được đánh số từ ~1~ tới ~n~. Hãy đếm số đường đi có ~k~ bước (cạnh) và in ra kết quả theo modulo ~10^9 + 7~. Một đường đi có thể có ghé thăm các đỉnh và cạnh nhiều lần.

Input

• Dòng đầu là ~3~ số nguyên ~n,\ m,\ k~ ~(1 \le n \le 100,\ 0 \le \ m \le n\cdot (n-1),\ 1 \le k \le 10^9)~ lần lượt là số đỉnh, số cạnh và số bước của đường đi.

• ~m~ dòng tiếp theo mô tả các cạnh của đồ thị. Dòng thứ ~i~ gồm ~2~ số nguyên ~a_i,\ b_i~ ~(1 \le a_i,\ b_i \le n, a_i \neq b_i)~ thể hiện đường đi từ đỉnh ~a_i~ tới đỉnh ~b_i~. Đồ thị đã cho đảm bảo không có khuyên và mỗi cạnh không xuất hiện quá một lần.

Output

In ra một dòng chứa số đường đi thoả mãn yêu cầu input theo modulo ~1000000007~.

Sample Input 1

3 4 2
1 2
2 3
3 1
2 1

Sample Output 1

5

Sample Input 2

5 10 11
2 3
4 2
2 1
2 4
1 5
5 2
3 2
3 1
3 4
1 2

Sample Output 2

21305

Giải thích

Ở ví dụ này, ta được cho đồ thị chứa ~3~ đỉnh và ~4~ cạnh như sau:

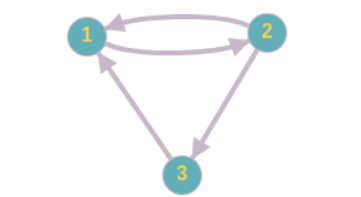
Có ~5~ đường đi với số bước ~k = 2~:

• ~1\rightarrow2\rightarrow1~
• ~1\rightarrow2\rightarrow3~
• ~2\rightarrow1\rightarrow2~
• ~2\rightarrow3\rightarrow1~
• ~3\rightarrow1\rightarrow2~