Bạn được cho một đồ thị có hướng gồm ~n~ đỉnh và ~m~ cạnh, các đỉnh được đánh số từ ~1~ tới ~n~ .

Đỉnh ~s~ được gọi là đến được đỉnh ~t~ trong ~k~ bước nếu như tồn tại một dãy ~k + 1~ đỉnh với đỉnh đầu tiên là đỉnh ~s~, đỉnh cuối cùng là đỉnh ~t~, sao cho luôn có đường đi trực tiếp giữa ~2~ đỉnh liên tiếp.

Bạn cần trả lời ~q~ truy vấn: cho ~3~ số ~s,\ k,\ t~, đếm số đường đi từ ~s~ tới ~t~ gồm đúng ~k~ bước. Một đường đi có thể đi qua một đỉnh hoặc một cạnh nhiều lần. Vì kết quả có thể rất lớn, hãy in ra số đường đi theo modulo ~10^9 + 7~.

Input

• Dòng đầu là ~3~ số nguyên ~n,\ m,\ q~ ~(1 \le n,\ q \le 200, 0 \le m \le n \cdot (n - 1))~ lần lượt là số đỉnh, số cạnh và số truy vấn.

• ~m~ dòng tiếp theo mô tả các cạnh của đồ thị. Dòng thứ ~i~ gồm ~2~ số nguyên ~a_i,\ b_i~ ~(1 \le a_i,\ b_i \le n, a_i \neq b_i)~ thể hiện đường đi từ đỉnh ~a_i~ tới đỉnh ~b_i~. Đồ thị đã cho đảm bảo không có các cạnh lặp lại nhau.

• ~q~ dòng tiếp theo thể hiện các truy vấn. Mỗi dòng gồm ~3~ số nguyên ~s,\ t,\ k~ ~(1 \le s,\ t \le n,\ 1 \le k \le 10^9)~, lần lượt điểm xuất phát, điểm kết thúc và độ dài của một đường đi.

Output

Với mỗi truy vấn, in ra một dòng chứa đáp án theo modulo ~1000000007~, là câu trả lời cho truy vấn ấy.

Sample Input

3 4 4
1 2
2 3
3 1
2 1
1 2 6
3 3 5
1 3 1
3 2 54

Sample Output

2
1
0
922111

Giải thích

Ở ví dụ này, ta được cho đồ thị chứa ~3~ đỉnh và ~4~ cạnh như sau:

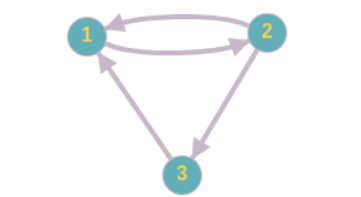
• ~1\rightarrow2\rightarrow3\rightarrow1\rightarrow2\rightarrow1\rightarrow2~
• ~1\rightarrow2\rightarrow1\rightarrow2\rightarrow3\rightarrow1\rightarrow2~