Ở thị trấn bedao, mọi người rất tin vào tâm linh. Họ quan niệm rằng, những vật dụng gắn liền với một số thần kỳ sẽ mang lại may mắn cho họ. Với họ, số thần kỳ là hiệu của ~2~ số chính phương hay nếu ~c~ là một số thần kỳ thì ~c = b^2 - a^2~. Tahp, một cư dân sống tại thị trấn, muốn chọn một số thần kỳ để làm biển hiệu cho chiếc xe mới mua. Tuy vậy, tahp không biết chọn số nào cho hợp lý. Anh ta có một số ~c~, bạn hãy tính xem ~c~ có phải số thần kỳ hay không nhé!

Input

Gồm ~1~ dòng chứa số nguyên ~c~ ~(1 \le c \le 10^9)~.

Output

Nếu ~c~ là một số thần kỳ, in ra kết quả theo trình tự sau:

• Dòng đầu tiên in ra YES.
• Dòng thứ hai in ra căn bậc hai của hai số chính phương thỏa mãn hiệu của chúng là ~c~. Nếu có nhiều cặp ~a~, ~b~ thỏa mãn, in ra cặp ~a~, ~b~ bất kì ~(1 \leq a \leq b \leq 10^9)~

Nếu ~c~ không phải là một số thần kỳ, in ra NO.

Subtask

~30\%~ số test có ~1 \le c \le 10^5~

~70\%~ số test còn lại không có ràng buộc gì thêm.

Sample Input

16

Sample Output

YES
5 3

Note

Ở test ví dụ, ~16~ là một số thần kỳ vì ~16 = 5^2-3^2~

nkwn đố egg một bài toán như sau: Cho một xâu ~s~ chỉ chứa những chữ cái in thường. Xâu con ~sub[l...r]~ được gọi là xâu con lí tưởng nếu:

• Độ dài xâu ~sub~ là ~2~, ~sub[l] = sub[r]~,
• Độ dài xâu ~sub~ lớn hơn ~2~, ~sub[l] = sub[r]~ và xâu con ~sub[l + 1, r - 1]~ chỉ chứa một loại kí tự khác với ~sub[l]~ và ~sub[r]~.

Ví dụ, ~abba~, ~bb~ là một xâu lí tưởng, trong khi ~abc~ không phải. Hãy giúp egg hoàn thành bài toán đó nhé!

Input

• Gồm ~1~ dòng chứa xâu ~s~ (~1 \le |s| \le 10^5)~.

Output

• Gồm một số nguyên duy nhất là số xâu con lí tưởng của xâu ~s~

Subtask

• ~20\%~ số test có (~1 \le |s| \le 100)~.

• ~80\%~ số test còn lại không có ràng buộc gì thêm.

Sample Input

abbcba

Sample Output

2

Note

• Ở test ví dụ, có 2 xâu con tốt: ~bb~ và ~bcb~

Rimuru vừa được isekai đến thế giới mới. Trong chuyến phiêu lưu vào hang của ~fan MU~, Rimuru gặp Veldora tempest và muốn cậu ta hòa vào trong cơ thể của mình. Để chứng minh mình có đủ trình để mang rồng Veldora ra khỏi hang của những con quỷ đỏ Rimuru được Veldora thử thách một bài toán:

Được biết chênh lệch giữa 2 số ~a~ và ~b~ là ~|a-b|~, ta cần xếp ~N~ con slime vào các hàng sao cho :

• Chênh lệch số slime giữa 2 hàng liên tiếp đều bằng ~0~ hoặc đều bằng ~1~.
• Chênh lệch số slime giữa 2 hàng bất kỳ không vượt quá ~1~.

Lưu ý : Ta có thể chia tất cả ~N~ con slime vào 1 hàng và cách chia này luôn đúng.

Với mỗi cách xếp, ta gọi tempest của cách xếp đó là chênh lệch giữa số slime nhiều nhất của ~1~ hàng và số hàng của cách xếp đó. Bạn hãy giúp Rimuru hấp thụ Veldora tempest và thoát khỏi hang ~MU~ bằng cách tính tempest nhỏ nhất trong tất cả các cách chia ~N~ con slime.

Input

Gồm ~1~ dòng chứa số nguyên dương ~N~ ~(1 \le N \le 10^{12})~.

Output

In ra kết quả là tempest nhỏ nhất có thể.

Subtask

• ~20\%~ số test có ~N \le 10^{3}~.
• ~30\%~ số test tiếp theo có ~N \le 10^{6}~.
• ~50\%~ số test còn lại không có điều kiện gì thêm.

Sample Input

6

Sample Output

1

Note

Ta chia các con slime thành ~2~ hàng :

• Hàng đầu có ~3~ con slime.
• Hàng thứ nhì có ~3~ con slime.
• Vậy tempest ~= 3 - 2 ~.

Copium rất thích xúc xích. Một hôm anh ta đi vào cửa hàng tiện lợi, cửa hàng có ~N~ cái xúc xích được bày sẵn, cái thứ ~i~ có chiều dài là ~a_i~. Copium chỉ muốn mua ~4~ cái từ cửa hàng, nhưng việc lựa ~4~ cây xúc xích của Copium rất đặc biệt, anh ta chỉ chọn ~4~ cây ở vị trí ~i~, ~j~, ~k~, ~l~ ~(1 \le i < j < k < l \le N)~ nếu cây thứ nhất có cùng chiều dài với cây cuối cùng, và cây thứ ~2~ cùng chiều dài với cây thứ ~3~. Nói cách khác ~a_i = a_l~ và ~a_j = a_k~.

Copium rất tò mò số cách để chọn ~4~ cây thoả mãn điều kiện như trên, bạn có thể giúp anh ấy không?

Input

• Dòng đầu tiên gồm số nguyên ~N~, biểu diễn số xúc xích có trong cửa hàng ~(1 \le N \le 10^5)~
• Dòng tiếp theo gồm ~N~ số nguyên ~a_1, a_2, ..., a_n~ là chiều dài của các cây xúc xích ~(1 \le a_i \le 100)~

Output

• In ra số cách để chọn ~4~ cây xúc xích thoả mãn điều kiện đã cho.

Subtask

• ~15\%~ số test có ~1 \le N \le 100~
• ~15\%~ số test tiếp theo có ~1 \le N \le 1000~
• ~20\%~ số test tiếp theo có ~1 \le N \le 5000~
• ~50\%~ số test còn lại không có điều kiện gì thêm

Sample Input 1

8
2 1 3 4 2 1 2 3

Sample Output 1

2

Sample Input 2

8
1 3 3 7 1 3 3 7

Sample Output 2

3

Cho một cây có ~n~ đỉnh và ~n - 1~ cạnh. Một đỉnh ~i~ khác đỉnh gốc có cha trên cây là đỉnh ~p_i~, còn nếu ~i~ là gốc thì ~p_i = 0~. Mỗi đỉnh trên cây còn có một giá trị gọi là giá trị của đỉnh, ban đầu giá trị của tất cả các đỉnh đều bằng ~1~.

Cho một dãy ~a~ là thứ tự xét các đỉnh, tại mỗi đỉnh ~u~ được xét cần thực hiện biển đổi sau:

• Với mỗi đỉnh ~v~ thuộc đường đi từ đỉnh gốc đến đỉnh cha của đỉnh ~u~, tăng giá trị của đỉnh ~v~ một lượng bằng với giá trị đỉnh ~u~.

Với mỗi đỉnh trên cây, hãy cho biết giá trị của đỉnh đó tính đến thời điểm nó được thăm là bao nhiêu, in ra phần dư của kết quả khi chia cho ~10^9 + 7~.

Input

• Dòng đầu tiên chứa số nguyên dương ~n~ - số đỉnh trên cây ~(1 \le n \leq 10^5)~.

• Dòng thứ hai chứa ~n~ số ~p_1, p_2,..., p_n~. ~(1 \le p_i \le n)~

• Dòng thứ ba chứa ~n~ số ~a_1, a_2,..., a_n~. ~(1 \le a_i \le n)~

Output

• In ra ~n~ dòng, dòng thứ ~i~ chứa một số duy nhất là giá trị đỉnh ~i~ tính đến thời điểm đỉnh ~i~ được xét chia lấy dư cho ~10^9 + 7~.

Subtask

• ~20\%~ số test có ~n \leq 1000~.
• ~80\%~ số test còn lại không có ràng buộc gì thêm.

Sample Input 1

6
2 3 0 5 3 5
1 4 6 5 2 3

Sample Output 1

1 2 9 1 3 1 

Note

• Giá trị ban đầu của các đỉnh: ~[1, 1, 1, 1, 1, 1]~
• ~1~: ~[1, 2, 2, 1, 1, 1]~
• ~4~: ~[1, 2, 3, 1, 2, 1]~
• ~6~: ~[1, 2, 4, 1, 3, 1]~
• ~5~: ~[1, 2, 7, 1, 3, 1]~
• ~2~: ~[1, 2, 9, 1, 3, 1]~
• ~3~: ~[1, 2, 9, 1, 3, 1]~

Chị Hiền là một người đam mê toán học. Một hôm nọ, chị gặp phải một bài toán như sau:

Cho mảng ~A~ gồm ~n~ phần tử ~A_1, A_2, \dots, A_n~. Chọn ra ~B~ là một dãy con không rỗng từ mảng ~A~ ~(~các phần tử của ~B~ không nhất thiết phải nằm liên tiếp~)~, đặt ~m~ ~(m > 0)~ là số phần tử của ~B~, lần lượt thực hiện các thao tác sau:

• Xét mặt phẳng ~Oxy~, một điểm được gọi là lattice point nếu nó có tọa độ là số nguyên dương. Chọn ra ~m~ điểm sao cho chúng đều là lattice point. Điểm thứ ~i~ phải nằm trên đường thẳng đi qua điểm ~(0, B_i)~ và ~(B_i, 0)~. Lưu ý rằng các điểm được chọn có thể ở cùng tọa độ.

• Tiếp theo, kẻ ~m~ đoạn thẳng, đoạn thứ ~i~ nối giữa gốc tọa độ ~(0, 0)~ và điểm thứ ~i~. Độ đẹp của ~1~ đoạn thẳng được tính bằng số lượng lattice point nằm trên đoạn thẳng đó.

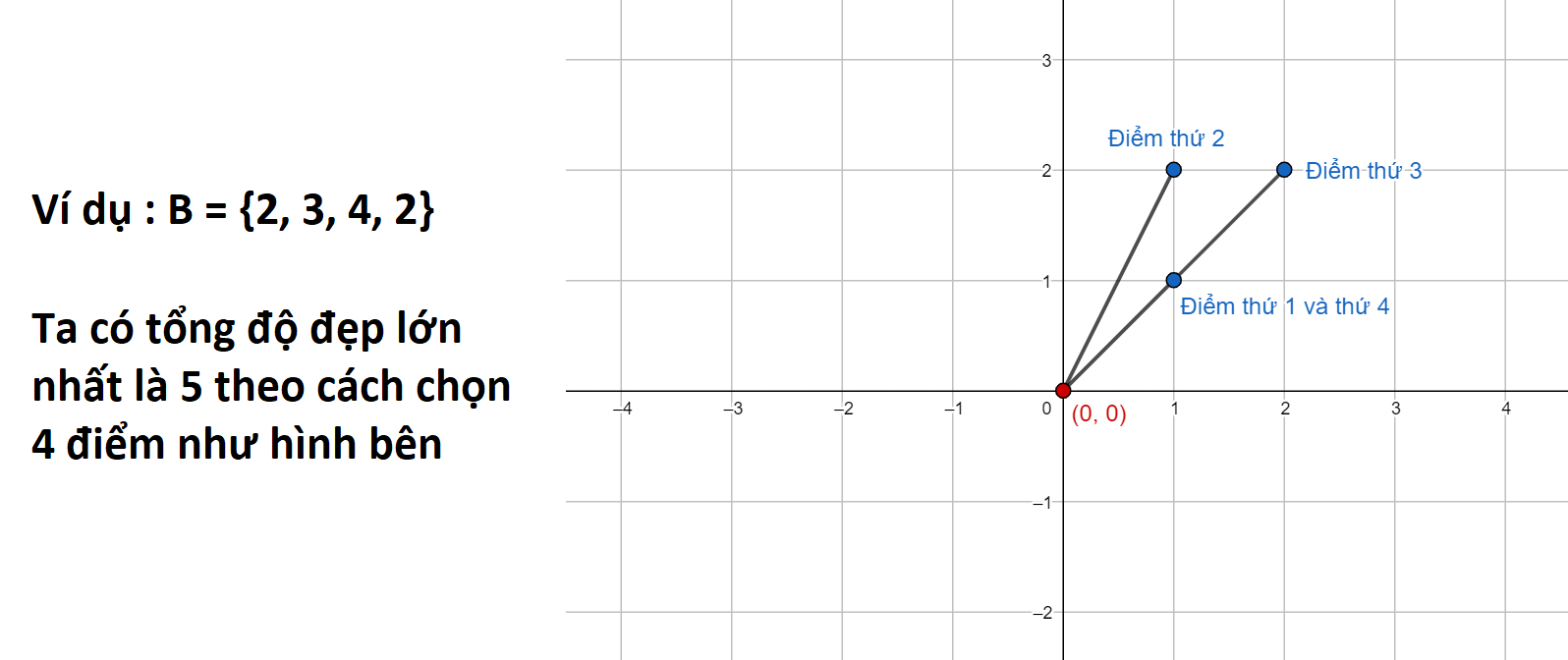
Với mỗi đãy con ~B~ được chọn, gọi ~f(B)~ là số cách chọn ~m~ điểm sao cho tổng độ đẹp của ~m~ đoạn thẳng là tối đa, 2 cách chọn là khác nhau nếu tồn tại số nguyên dương ~i~ ~(i \le m)~ sao cho điểm thứ ~i~ trong cách chọn thứ 1 có tọa độ khác điểm thứ ~i~ trong cách chọn thứ 2. Gọi ~s(A)~ là tổng các ~f(B)~ với mọi dãy con ~B~ không rỗng của ~A~ (Có tổng cộng ~2^n - 1~ dãy con ~B~ không rỗng có thể chọn từ mảng ~A~ ban đầu).

Mặc dù ban đầu mảng ~A~ có ~n~ phần tử nhưng để tiết kiệm giấy một vài trong số chúng sẽ bị chị Hiền xóa đi. Cho ~q~ truy vấn, truy vấn thứ ~i~ gồm ~1~ cặp số ~l_i~ và ~r_i~ ~(1 \le l_i \le r_i \le n)~, hãy tính số giá trị khác nhau mà ~s(A)~ có thể nhận sau khi xóa nếu chị Hiền được phép giữ lại một số phần tử trong đoạn ~A_{l_i}, A_{l_i + 1}, \dots, A_{r_i}~ rồi xóa đi các phần tử còn lại của mảng ~A~ ~(~lưu ý rằng chị Hiền phải giữ ít nhất 1 phần tử để mảng ~A~ không rỗng sau khi xóa~)~. Do đáp án có thể rất lớn nên hãy lấy phần dư khi chia cho ~10^9 + 7~.

Hãy giúp chị Hiền trả lời ~q~ truy vấn trên.

Input

• Dòng đầu tiên chứa ~2~ số nguyên ~n~ và ~q~ ~(1 \le n,q \le 10^5)~.
• Dòng tiếp theo chứa ~n~ số nguyên ~A_1, A_2, \dots, A_n~ ~(2 \le A_i \le 10^{12}~, ~max(A_1, \ldots, A_n) - min(A_1, \ldots, A_n) < 10^7)~.
• ~q~ dòng tiếp theo, dòng thứ ~i~ chứa ~2~ số nguyên ~l_i~ và ~r_i~ ~(1 \le l_i \le r_i \le n)~.

Output

• Gồm ~q~ dòng, dòng thứ ~i~ là số giá trị khác nhau mà ~s(A)~ có thể nhận tương ứng với truy vấn thứ ~i~. Do đáp án có thể rất lớn nên hãy lấy phần dư khi chia cho ~10^9 + 7~.

Subtask

• Subtask ~1~ (~10\%~ số điểm): ~A_i~ là các số nguyên dương chẵn.
• Subtask ~2~ (~30\%~ số điểm): ~1 \le q \le 100~.
• Subtask ~3~ (~60\%~ số điểm): Không có ràng buộc gì thêm.

Sample Input

4 2
2 3 4 2
1 3
3 4

Sample Output

5
2

Note

• Truy vấn ~[1, 3]~ có tất cả ~5~ giá trị ~s(A)~ khác nhau :
  • ~A = [2]~: ~s(A) = 1~
  • ~A = [3]~: ~s(A) = 2~
  • ~A = [4]~: ~s(A) = 1~
  • ~A = [2, 3]~: ~s(A) = 5~
  • ~A = [2, 4]~: ~s(A) = 3~
  • ~A = [3, 4]~: ~s(A) = 5~
  • ~A = [2, 3, 4]~: ~s(A) = 11~