Tạp chí VNOI Xuân Bính Ngọ - Coding Challenge #04
unknownnaciul
đã đăng vào 10, Tháng 2, 2026, 1:00
Coding Challenge
Coding Challenge là một chuyên mục thuộc Tạp chí VNOI, được xây dựng với mục tiêu mang đến cho cộng đồng lập trình thi đấu Việt Nam một sân chơi hữu ích và thiết thực nhằm giúp các độc giả củng cố kiến thức thuật toán và thúc đẩy tinh thần học hỏi, chia sẻ trong cộng đồng.
Hoạt động được tổ chức định kỳ hai lần mỗi tháng trên Fanpage VNOI, Group Facebook “Diễn đàn Tin học Việt Nam” và nền tảng chấm bài trực tuyến VNOJ. Toàn bộ các bài toán trong Coding Challenge được biên soạn bởi đội ngũ Tình nguyện viên thuộc Team Contest của VNOI. Chất lượng các bài toán Coding Challenge được đảm bảo về tính chuyên môn, có sự đa dạng về chủ đề và độ khó cũng như đáp ứng yêu cầu về tính chặt chẽ và chính xác.
Độc giả của Tạp chí VNOI có thể tham gia giải các bài toán thuộc Coding Challenge và gửi lời giải về cho Tạp chí. Những bài giải chất lượng sẽ được chọn lọc để đăng tải trong các số Tạp chí tiếp theo. Bên cạnh việc được ghi nhận và giới thiệu rộng rãi đến cộng đồng, các tác giả có lời giải được đăng tải sẽ nhận những phần quà tri ân từ VNOI nhằm khuyến khích tinh thần ham học hỏi và chia sẻ kiến thức đến cộng đồng
Các lời giải được chọn lọc để đăng công khai sẽ được đánh giá dựa trên tiêu chí về sự rõ ràng, mạch lạc, sáng tạo; có sự đầu tư trong diễn giải tư duy, cấu trúc và tính dễ hiểu. Đối với các bài toán có nhiều subtask, tác giả cần trình bày đầy đủ ý tưởng và hướng giải quyết cho tất cả các phần.
Phần thưởng dành cho mỗi lời giải được đăng tải trên Tạp chí là một bộ quà tặng gồm sổ tay, bút, sticker và móc khóa. Đặc biệt, với các tác giả có từ 03 bài giải trở lên được đăng trong chuyên mục, Ban biên tập Tạp chí sẽ gửi tặng một chiếc áo VNOI như lời tri ân cho những đóng góp tích cực đối với Coding Challenge.
Tiếp nối 03 số đầu tiên, các Coding Challenge #04, #05, #06 và #07 tiếp tục ghi nhận sự ủng hộ nhiệt tình của cộng đồng lập trình thi đấu. Hệ thống đã ghi nhận tổng cộng 2086 lượt nộp bài và ~x~ lời giải được gửi về cho Tạp chí.
Đội ngũ tạp chí VNOI xin gửi lời cảm ơn chân thành đến tất cả các bạn đã tích cực tham gia các Coding Challenge và đóng góp những lời giải vô cùng chất lượng trong thời gian qua!
Coding Challenge #4
Coding Challenge #4 có tên là Cân xu. Đây là bài toán mở rộng từ bài toán Quy hoạch động trên đồ thị có hướng không chu trình (DAG). Để giải quyết được bài toán lần này, yêu cầu các bạn thí sinh phải đưa ra nhiều nhận xét một cách khéo léo để biến đổi bài toán về một bài tập cấu trúc dữ liệu kinh điển.
Bài toán Cân xu đã được 362 thí sinh thử sức và có 9 lời giải xuất sắc đạt được số điểm tối đa.
Để hiểu rõ hơn về lời giải của bài toán, mời các bạn theo dõi lời giải xuất sắc do bạn Nguyễn Hoàng Minh biên soạn.
Đề bài
Bạn đọc có thể theo dõi đề bài gốc và subtasks tại nền tảng VNOJ. Sau đây là bản tóm tắt của đề bài.
Cho ~n~ đồng xu có trọng lượng phân biệt và ~m~ mối liên hệ không mâu thuẫn nhau có dạng ~x > y~, cho biết đồng xu ~x~ nặng hơn đồng xu ~y~. Gọi cấp bậc của một đồng xu là thứ tự của nó khi sắp xếp các đồng xu theo trọng lượng.
Với mỗi đồng xu, ta cần xác định giá trị ~k~ sao cho có thể xác định chính xác cấp bậc của đồng xu đó mà chỉ sử dụng ~k~ mối liên hệ đầu tiên; hoặc cho biết không thể xác định cấp bậc của đồng xu khi sử dụng cả ~m~ mối liên hệ.
Giới hạn:
- ~2 \leq n \leq 2 \cdot 10^5~.
- ~1 \leq m \leq 8 \cdot 10^5~.
Lời giải
Subtask 1
Giới hạn: ~n \leq 7~; ~m \leq 20~
Ý Tưởng
Đặt ~P~ là thứ tự của các đồng xu được sắp xếp tăng dần theo cấp bậc của chúng. Với định nghĩa này, ta có thể biểu diễn ~P~ bằng một hoán vị của ~n~ số tự nhiên đầu tiên.
Ví dụ
Với ~n = 3~, ~P = (2, 3, 1)~ có thể được hiểu như:- Đồng xu ~2~ có cấp bậc là ~1~;
- Đồng xu ~3~ có cấp bậc là ~2~;
- Đồng xu ~1~ có cấp bậc là ~3~.
- Đặt ~e_i = (x_i, y_i)~ là cặp đồng xu được cân ở lần cân thứ ~i~ (~1 \leq i \leq m~; đồng xu ~x_i~ nặng hơn đồng xu ~y_i~). Đặt ~E_j = \{e_i \vert 1 \leq i \leq j \}~ là tập hợp cặp đồng xu của ~i~ lần cân đầu tiên.
Ta gọi một thứ tự ~P~ là hợp lệ với một tập hợp lần cân ~E~ nếu không tồn tại một cặp đồng xu nào mà thứ tự của chúng không thỏa kết quả của một lần cân nào đó trong ~E~.
Nói cách khác, nếu ~(x, y) \in E~ thì vị trí của đồng xu ~y~ phải nằm phía trước vị trí của đồng xu ~x~ trong ~P~ (đồng xu ~x~ có cấp bậc cao hơn đồng xu ~y~).
Vì dữ liệu đầu vào đảm bảo rằng các kết quả cân không mâu thuẫn với nhau, ít nhất một thứ tự hợp lệ phải tồn tại với tập hợp ~m~ lần cân (~E_m~).
Cấp bậc của đồng xu ~z~ là có thể chắc chắn xác định được với tập hợp lần cân ~E~ nếu trong mọi thứ tự ~P~ hợp lệ so với ~E~, cấp bậc của ~z~ không đổi (tạm gọi đây là điều kiện ~(1)~).
Vì vậy, nếu ta chỉ kiểm tra rằng cấp bậc của từng đồng xu có thể hay không thể được xác định (và đạt ~50~% số điểm của subtask 1), ta có thể:
- Duyệt qua tất cả ~n!~ hoán vị để tìm các thứ tự hợp lệ; và
Với mỗi đồng xu, ta kiểm tra liệu có tồn tại hai thứ tự hợp lệ khác nhau mà cấp bậc của đồng xu trong hai thứ tự đó là khác nhau.
- Với mỗi đồng xu ~z~, việc tìm được thời điểm sớm nhất mà có thể chắc chắn xác định cấp bậc của đồng xu đó sẽ tương đương với việc tìm ra tập hợp gồm các lần cân đầu tiên với kích thước nhỏ nhất sao cho điều kiện ~(1)~ vẫn thỏa.
Nói cách khác, ta cần tìm ~i~ nhỏ nhất sao cho với ~E_i~, cấp bậc ~z~ có thể chắc chắn xác định.
Để thực hiện điều này, ta có thể duyệt qua một tập hợp lần cân và thực hiện kiểm tra như trên.
Độ Phức Tạp
- Ý tưởng nêu trên có thể được cài đặt với độ phức tạp thời gian ~O(m \cdot n! \cdot (m + n))~.
- Ta cần duyệt qua ~O(m)~ tập hợp lần cân.
- Với mỗi tập hợp, ta cần duyệt qua ~O(n!)~ hoán vị để tìm các thứ tự hợp lệ.
- Với mỗi thứ tự, ta thực hiện kiểm tra tính hợp lệ bằng cách duyệt qua ~O(m)~ lần cân. Nếu thứ tự hợp lệ, chúng ta cần phải kiểm tra cấp bậc của ~O(n)~ đồng xu có khác so với thứ tự hợp lệ khác không.
Code Minh Họa
Code C++ minh họa
#include <bits/stdc++.h>
using namespace std;
template<class A, class B> bool maximize(A &a, const B &b) { return (a < b) ? (a = b, true) : false; }
template<class A, class B> bool minimize(A &a, const B &b) { return (a > b) ? (a = b, true) : false; }
constexpr int MAX_N = 200'005, MAX_M = 800'005, INF = 0X3F3F3F3F, NINF = 0XC0C0C0C0;
int n, m, x[MAX_M], y[MAX_M];
void input() {
cin >> n >> m;
for (int i = 0; i < m; ++i) {
cin >> x[i] >> y[i];
--x[i];
--y[i];
}
}
vector<int> findPositions(const vector<int> &permutation) {
const int n = permutation.size();
vector<int> positions(n);
for (int i = 0; i < n; ++i)
positions[permutation[i]] = i;
return positions;
}
bool checkValid(const vector<int> &order, const int e) {
const vector<int> &positions(findPositions(order));
for (int i = 0; i < e; ++i)
if (positions[x[i]] > positions[y[i]])
return false;
return true;
}
bool checkInvalid(const vector<int> &order, const int e) {
return !checkValid(order, e);
}
vector<int> findLevels(const int e) {
vector<int> levels(n, n), permutation(n);
/**
level = -1 : The level cannot be determined
level = n : The level has not been determined yet
(as there is no contradiction, there should no final result with this value)
0 <= level < n : The level is currently determined
**/
iota(permutation.begin(), permutation.end(), 0);
do {
if (checkInvalid(permutation, e))
continue;
for (int i = 0; i < n; ++i) {
const auto &value = permutation[i];
auto &level = levels[value];
if (level < 0)
continue;
if (level == n) {
level = i;
continue;
}
if (level != i)
level = -1;
}
} while (next_permutation(permutation.begin(), permutation.end()));
return levels;
}
vector<int> findWhen() {
vector<int> result(n, -1);
for (int e = 1, i = 0; e <= m; ++e) {
const auto &levels(findLevels(e));
for (i = 0; i < n; ++i) {
if (result[i] >= 0 || levels[i] < 0)
continue;
result[i] = e;
}
}
return result;
}
int main() {
#ifdef LOCAL
freopen("input.INP", "r", stdin);
#endif // LOCAL
cin.tie(0) -> sync_with_stdio(0);
cout.tie(0);
input();
for (const int &e : findWhen())
cout << e << ' ';
cout << '\n';
return 0;
}
Subtask 2
Giới hạn: ~n \leq 100~; ~m \leq 400~
Ý Tưởng
- Ta có thể biểu diễn mối quan hệ trọng lượng tương đối bằng cách dựng một đồ thị.
Cụ thể hơn, đặt ~G = (V, E)~ với:
- ~V~ là tập hợp các đồng xu
- ~E~ là tập hợp các lần cân: ~(x, y) \in E~ (tồn tại một cung trực tiếp từ ~x~ tới ~y~) nếu như tồn tại một lần cân xác định được rằng đồng xu ~x~ nặng hơn đồng xu ~y~.
- Ta nhận thấy rằng: đồng xu ~x~ có thể được xác định nặng hơn đồng xu ~y~ khi đồ thị ~G~ phải chứa ít nhất một đường đi từ ~x~ tới ~y~.
Giải thích
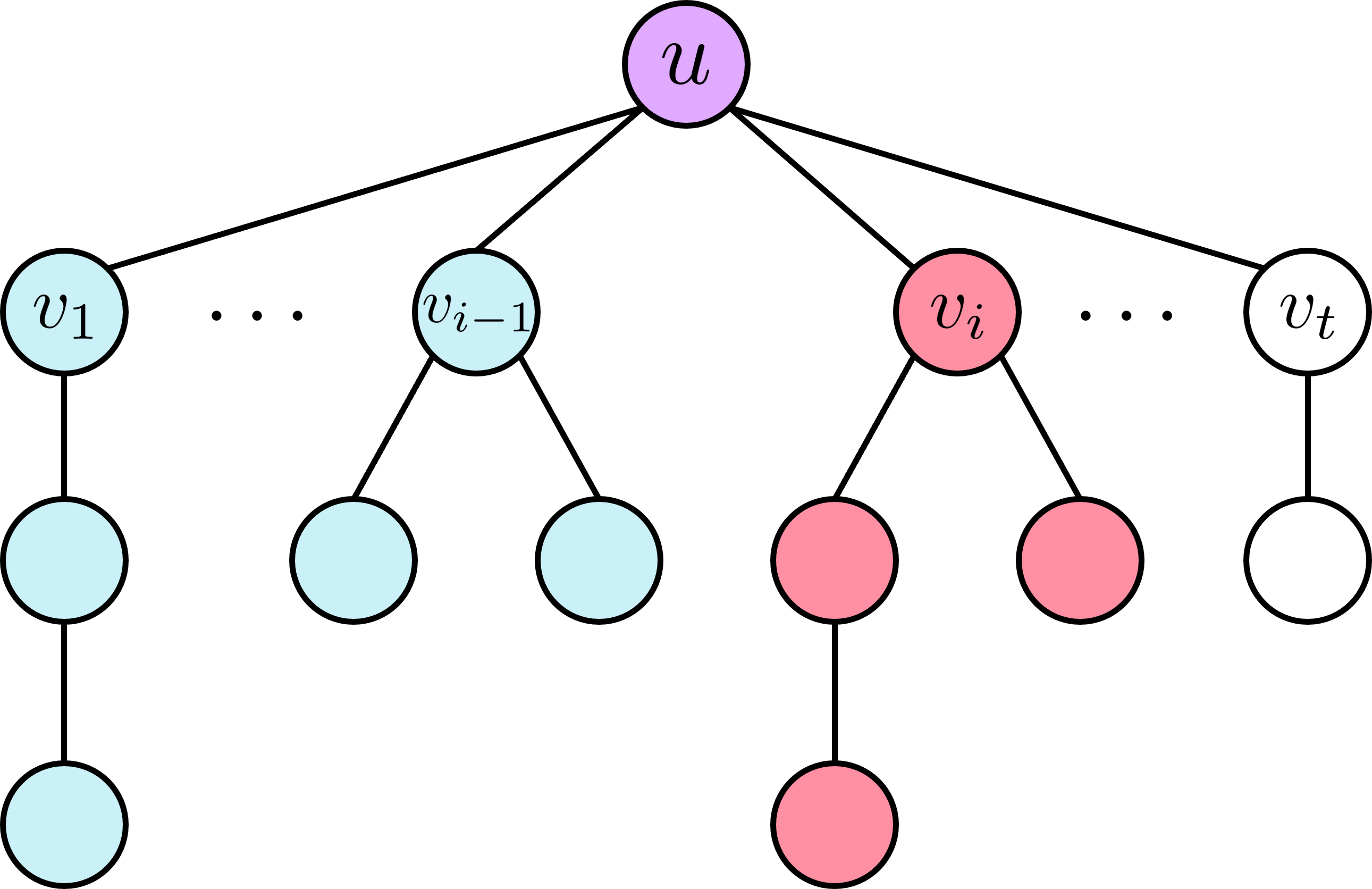
- Giả sử đường đi từ ~x~ tới ~y~ là một dãy các đỉnh ~U_1, ..., U_k~ (với ~k \geq 2~, ~U_1 = x~, ~U_k = y~) thì theo cách ta dựng đồ thị, đồng xu ~U_i~ phải nặng hơn đồng xu ~U_{i + 1}~ (với ~1 \leq i < k~). Vì thế, dựa vào tích chất bắc cầu, ta có đồng xu ~U_1~ (hay ~x~) phải nặng hơn đồng xu ~U_k~ (hay ~y~).
- Tập hợp các đỉnh mà có thể đến được từ đỉnh ~x~ cũng đồng thời là tập hợp các đỉnh đại diện cho đồng xu có thể xác định nhẹ hơn đồng xu ~x~.
- Ta có thể xác định được tập hợp này bằng cách sử dụng các thuật toán duyệt đồ thị như BFS hoặc DFS trên đồ thị ~G~.
- Tương tự, tập hợp các đỉnh mà có thể đi tới được đỉnh ~x~ cũng đồng thời là tập hợp các đỉnh đại diện cho đồng xu nhẹ có thể xác định nặng đồng xu ~x~.
- Để xác định được tập hợp này, ta cũng có thể sử dụng các thuật toán duyệt đồ thị như trên nhưng trên một đồ thị có chiều các cạnh được đảo so với ~G~.
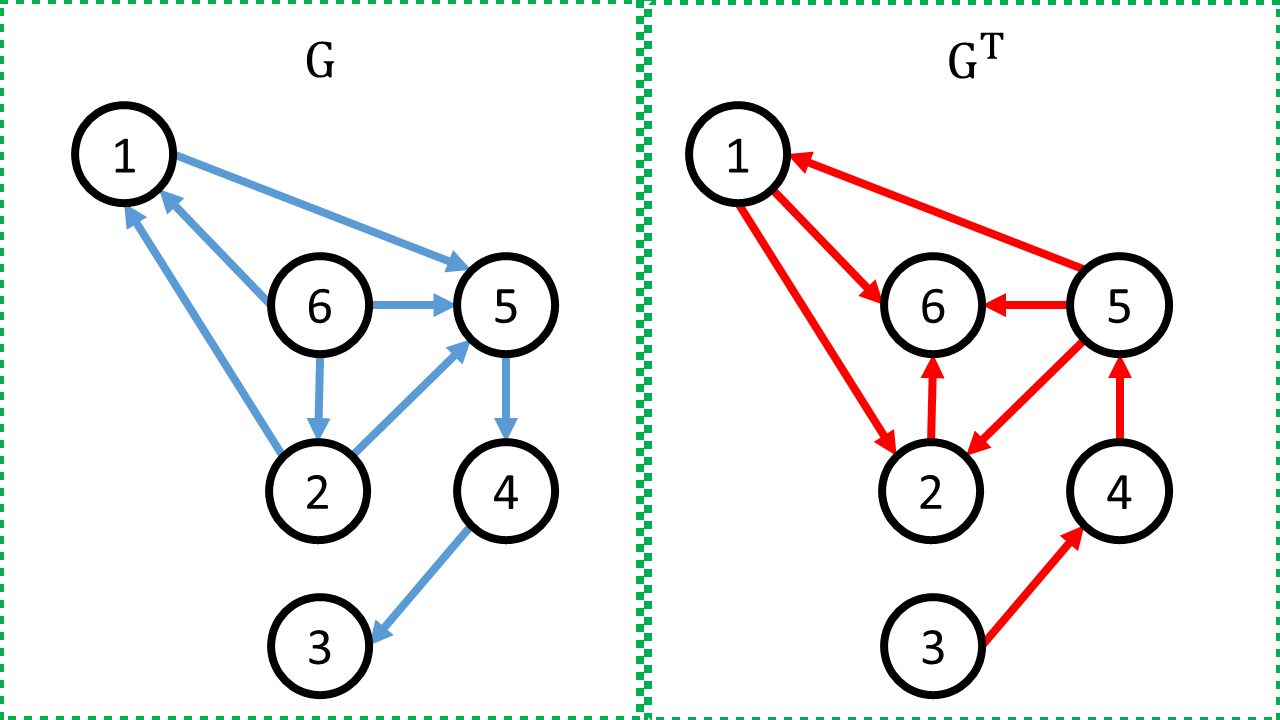
- Cụ thể hơn, ta có thể đặt ~G^T = (V, E^T)~ với ~E^T = \{(y, x) \vert (x, y) \in E\}~
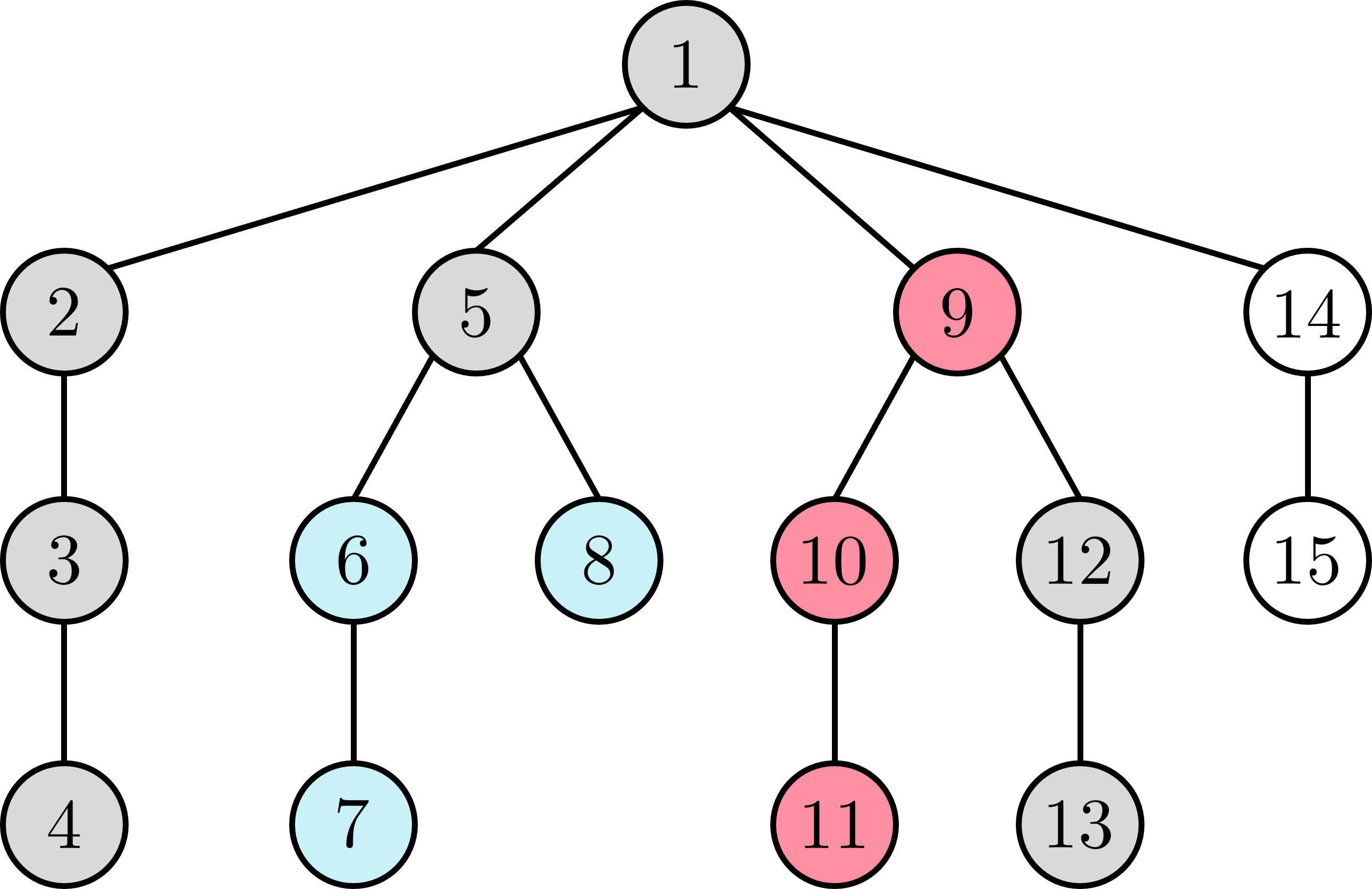
Minh họa đồ thị được dựng từ sample
- Đồ thị được dựng từ sample ~1~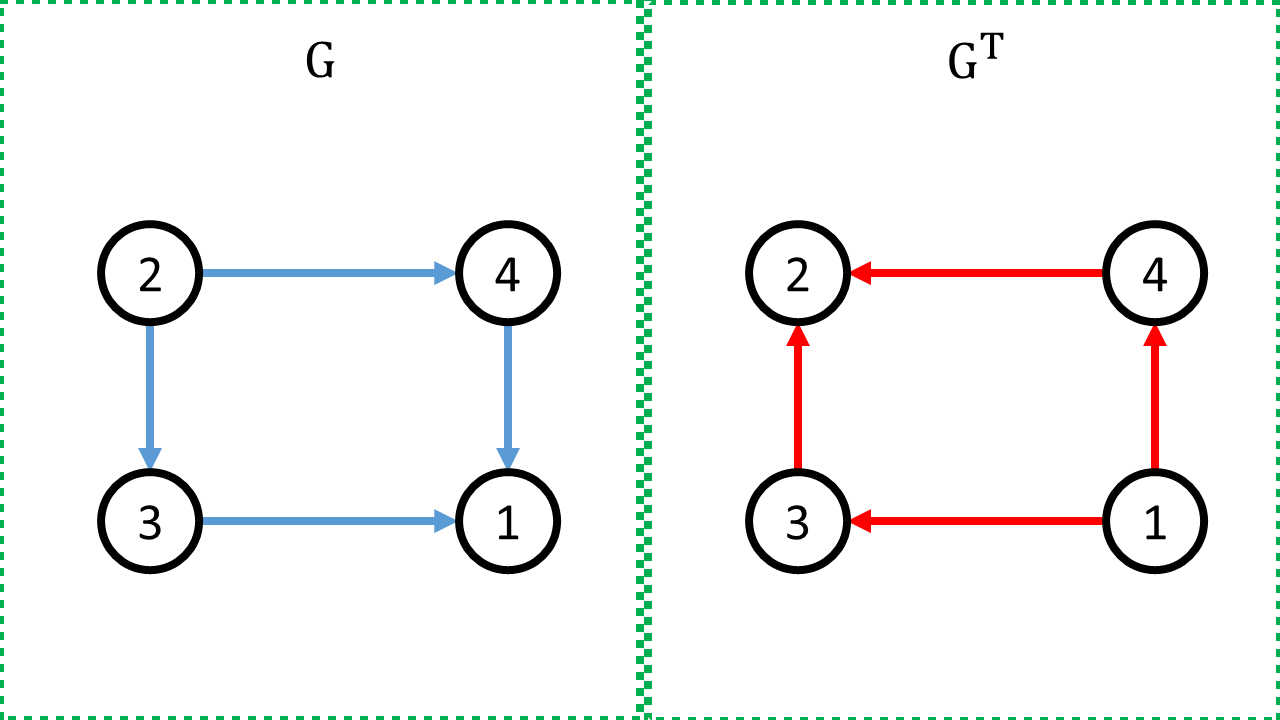
- Đồ thị được dựng từ sample ~2~
- Vì vậy, nếu ta chỉ muốn kiểm tra rằng cấp bậc của một đồng xu ~z~ có thể hay không thể được xác định (và đạt ~50~% số điểm của subtask 2, ta có thể thực hiện bằng cách kiểm tra phép hợp của hai tập hợp đến được từ ~z~ và có thể đi đến được ~z~ có chứa mọi đỉnh của đồ thị đã cho không (cấp bậc của đồng xu ~z~ chỉ có thể xác định khi trong lượng tương đối giữa nó và các đồng xu khác đều có thể xác định). Tạm gọi điều kiện của việc kiểm tra này là điều kiện ~(2)~.
- Tương tự như subtask 1, với mỗi đồng xu ~z~, việc tìm được thời điểm sớm nhất mà có thể chắc chắn xác định cấp bậc của đồng xu đó sẽ tương đương với việc tìm ra tập hợp gồm các lần cân đầu tiên với kích thước nhỏ nhất sao cho điều kiện ~(2)~ vẫn thỏa.
Độ Phức Tạp
- Ý tưởng nêu trên có thể được cài đặt với độ phức tạp thời gian ~O(n \cdot m \cdot (n + m))~.
Code Minh Họa
Code C++ minh họa
#include <bits/stdc++.h>
using namespace std;
template<class A, class B> bool maximize(A &a, const B &b) { return (a < b) ? (a = b, true) : false; }
template<class A, class B> bool minimize(A &a, const B &b) { return (a > b) ? (a = b, true) : false; }
constexpr int MAX_N = 200'005, MAX_M = 800'005, INF = 0X3F3F3F3F, NINF = 0XC0C0C0C0;
vector<pair<int, int> > graph[MAX_N], reversedGraph[MAX_N];
int n, m, x[MAX_M], y[MAX_M];
void input() {
cin >> n >> m;
for (int i = 1; i <= m; ++i) {
cin >> x[i] >> y[i];
graph[x[i]].emplace_back(i, y[i]);
reversedGraph[y[i]].emplace_back(i, x[i]);
}
}
namespace ReachabilityChecker {
bool visited[MAX_N];
int limit;
void runFirstDFS(const int x) {
visited[x] = true;
for (const auto &[e, y] : graph[x]) {
if (visited[y] || e > limit)
continue;
runFirstDFS(y);
}
}
void runSecondDFS(const int x) {
visited[x] = true;
for (const auto &[e, y] : reversedGraph[x]) {
if (visited[y] || e > limit)
continue;
runSecondDFS(y);
}
}
int check(const int source) {
for (int i = 1; i <= n; ++i)
visited[i] = false;
runFirstDFS(source);
runSecondDFS(source);
for (int i = 1; i <= n; ++i)
if (!visited[i])
return false;
return true;
}
}
void determineWhen() {
vector<int> result(n + 1, -1);
for (int e = 1, x = 0; e <= m; ++e) {
ReachabilityChecker::limit = e;
for (x = 1; x <= n; ++x) {
if (result[x] > 0)
continue;
if (ReachabilityChecker::check(x))
result[x] = e;
}
}
for (int i = 1; i <= n; ++i)
cout << result[i] << ' ';
cout << '\n';
}
int main() {
#ifdef LOCAL
freopen("input.INP", "r", stdin);
#endif // LOCAL
cin.tie(0) -> sync_with_stdio(0);
cout.tie(0);
input();
determineWhen();
return 0;
}
Subtask 3
Giới hạn: ~n \leq 1000~; ~m \leq 4000~
Ý Tưởng
- Subtask 3có thể được giải quyết theo nhiều cách khác nhau.
Cách Thứ Nhất
- Ta có nhận xét rằng, với đồng xu ~z~, nếu cấp bậc của ~z~ có thể được xác định với tập hợp ~E_i~, tập hợp của ~i~ lần cân đầu tiên, thì cũng có thể được xác định với ~E_j~ (với ~i < j \leq m~) vì ~E_i \subset E_j~. Vì vậy, thay vì duyệt tuần tự từng tập hợp lần cân (mỗi lần xét một thêm kết quả cân) như trong subtask 2, ta có thể sử dụng thuật toán chặt nhị phân để tìm được thời điểm sớm nhất.
Cách Thứ Hai
- Ý tưởng của cách thứ hai gần giống với thuật toán Prim (sử dụng trong cho bài toán tìm cây khung nhỏ nhất). Với mỗi cạnh ~e_i~ trong đồ thị ~G~ được định nghĩa trước đó, ta đặt trọng số của cạnh ~e_i~ là ~i~ (thời điểm cặp đồng xu mà ~e_i~ đại diện được cân).
- Với một đỉnh ~z~, ta đặt ~V^{+}_{z}~ là tập hợp các đỉnh có thể đến được từ ~z~ trong ~G~ (bao gồm cả ~z~). Ta nhận thấy rằng việc tìm thời điểm sớm nhất mà tập hợp ~V^{+}_{z}~ cũng sẽ tương đương với việc tối thiểu hóa trọng số lớn nhất trong cây chứa các cạnh ~V^{+}_{z}~.
- Tương tự, ta đặt ~V^{-}_{z}~ là tập hợp các đỉnh có thể đến được từ ~z~ trong ~G^{T}~ (bao gồm cả ~z~). Ta nhận thấy rằng việc tìm thời điểm sớm nhất mà tập hợp ~V^{-}_{z}~ cũng sẽ tương đương với việc tối thiểu hóa trọng số lớn nhất trong cây chứa các cạnh ~V^{-}_{z}~.
- Để tối thiểu hóa trong cả hai trường hợp, ta đều có thể thực hiện bằng cách:
- Khởi đầu với cây gồm một đỉnh ~z~ duy nhất;
- Lần lượt chọn cạnh với trọng số nhỏ nhất nối từ một đỉnh đã thuộc cây và một đỉnh chưa thuộc cây; Thêm cạnh và đỉnh của cạnh đó và cây; Thực hiện nhiều lần cho đến khi ta không thể mở rộng được cây nữa.
- Nếu ~V^{+}_{z} \cup V^{-}_{z} \neq V~ thì cấp bậc của ~z~ không thể xác định. Ngược lại, cấp bậc của ~z~ sẽ là giá trị lớn nhất trong hai trường hợp.
Độ Phức Tạp
- Ý tưởng trong cách thứ nhất có thể được cài đặt với độ phức tạp thời gian ~O(n \cdot \log m \cdot (n + m))~.
- Độ phức tạp có thể được phân tích gần như tương tự như trong Subtask 2 nhưng khi này, ta chỉ xét ~O(\log m)~ thay vì ~O(m)~ tập hợp lần cân.
- Ý tưởng trong cách thứ hai có thể được cài đặt với độ phức tạp thời gian ~O(n \cdot (n + m \log m))~.
- Ngoài ra, ý tưởng trong cách thứ hai cũng có thể được cài đặt với độ phức tạp thời gian ~O(n \cdot (n + m))~ nếu ta sử dụng một mảng danh sách đánh số theo chỉ số cạnh thay vì dùng heap bởi trọng số cạnh chỉ nằm trong đoạn từ ~1~ tới ~m~.
Code Minh Họa
Code C++ minh họa cho cách thứ nhất
#include <bits/stdc++.h>
using namespace std;
template<class A, class B> bool maximize(A &a, const B &b) { return (a < b) ? (a = b, true) : false; }
template<class A, class B> bool minimize(A &a, const B &b) { return (a > b) ? (a = b, true) : false; }
constexpr int MAX_N = 200'005, MAX_M = 800'005, INF = 0X3F3F3F3F, NINF = 0XC0C0C0C0;
vector<pair<int, int> > graph[MAX_N], reversedGraph[MAX_N];
int n, m, x[MAX_M], y[MAX_M];
void input() {
cin >> n >> m;
for (int i = 1; i <= m; ++i) {
cin >> x[i] >> y[i];
graph[x[i]].emplace_back(i, y[i]);
reversedGraph[y[i]].emplace_back(i, x[i]);
}
}
namespace ReachabilityChecker {
bool visited[MAX_N];
int limit;
void runFirstDFS(const int x) {
visited[x] = true;
for (const auto &[e, y] : graph[x]) {
if (visited[y] || e > limit)
continue;
runFirstDFS(y);
}
}
void runSecondDFS(const int x) {
visited[x] = true;
for (const auto &[e, y] : reversedGraph[x]) {
if (visited[y] || e > limit)
continue;
runSecondDFS(y);
}
}
int check(const int source) {
for (int i = 1; i <= n; ++i)
visited[i] = false;
runFirstDFS(source);
runSecondDFS(source);
for (int i = 1; i <= n; ++i)
if (!visited[i])
return false;
return true;
}
}
void determineWhen() {
for (int x = 1, low = 0, middle = 0, high = m; x <= n; ++x) {
ReachabilityChecker::limit = high = m;
if (!ReachabilityChecker::check(x)) {
cout << -1 << ' ';
continue;
}
low = 0;
while (low + 1 < high) {
middle = low + high >> 1;
ReachabilityChecker::limit = middle;
if (ReachabilityChecker::check(x))
high = middle;
else
low = middle;
}
cout << high << ' ';
}
cout << '\n';
}
int main() {
#ifdef LOCAL
freopen("input.INP", "r", stdin);
#endif // LOCAL
cin.tie(0) -> sync_with_stdio(0);
cout.tie(0);
input();
determineWhen();
return 0;
}
Code C++ minh họa cho cách thứ hai
#include <bits/stdc++.h>
using namespace std;
template<class A, class B> bool maximize(A &a, const B &b) { return (a < b) ? (a = b, true) : false; }
template<class A, class B> bool minimize(A &a, const B &b) { return (a > b) ? (a = b, true) : false; }
constexpr int MAX_N = 200'005, MAX_M = 800'005, INF = 0X3F3F3F3F, NINF = 0XC0C0C0C0;
vector<pair<int, int> > graph[MAX_N], reversedGraph[MAX_N];
int n, m, x[MAX_M], y[MAX_M];
bool visited[MAX_N];
void input() {
cin >> n >> m;
for (int i = 1; i <= m; ++i) {
cin >> x[i] >> y[i];
graph[x[i]].emplace_back(i, y[i]);
reversedGraph[y[i]].emplace_back(i, x[i]);
}
}
int findEarliestTime(const int source, vector<pair<int, int> > graph[]) {
priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > heap;
int maximum = 0;
heap.emplace(0, source);
visited[source] = false;
for (; !heap.empty();) {
const auto [t, x] = heap.top();
heap.pop();
if (visited[x])
continue;
maximize(maximum, t);
visited[x] = true;
for (const auto &[t, y] : graph[x]) {
if (visited[y])
continue;
heap.emplace(t, y);
}
}
return maximum;
}
int findEarliestTime(const int source) {
for (int i = 1; i <= n; ++i)
visited[i] = false;
const int maximum = max(findEarliestTime(source, graph), findEarliestTime(source, reversedGraph));
for (int i = 1; i <= n; ++i)
if (!visited[i])
return -1;
return maximum;
}
void determineWhen() {
for (int x = 1; x <= n; ++x)
cout << findEarliestTime(x) << ' ';
cout << '\n';
}
int main() {
#ifdef LOCAL
freopen("input.INP", "r", stdin);
#endif // LOCAL
cin.tie(0) -> sync_with_stdio(0);
cout.tie(0);
input();
determineWhen();
return 0;
}
Code C++ minh họa cho cách thứ hai
#include <bits/stdc++.h>
using namespace std;
template<class A, class B> bool maximize(A &a, const B &b) { return (a < b) ? (a = b, true) : false; }
template<class A, class B> bool minimize(A &a, const B &b) { return (a > b) ? (a = b, true) : false; }
constexpr int MAX_N = 200'005, MAX_M = 800'005, INF = 0X3F3F3F3F, NINF = 0XC0C0C0C0;
vector<pair<int, int> > graph[MAX_N], reversedGraph[MAX_N];
int n, m, x[MAX_M], y[MAX_M];
bool visited[MAX_N];
void input() {
cin >> n >> m;
for (int i = 1; i <= m; ++i) {
cin >> x[i] >> y[i];
graph[x[i]].emplace_back(i, y[i]);
reversedGraph[y[i]].emplace_back(i, x[i]);
}
}
int findEarliestTime(const int source, vector<pair<int, int> > graph[]) {
static queue<int> queues[MAX_M];
int maximum = 0;
visited[source] = false;
queues[0].push(source);
for (int t = 0; t <= m; ++t)
for (; !queues[t].empty(); queues[t].pop()) {
const auto &x = queues[t].front();
if (visited[x])
continue;
maximize(maximum, t);
visited[x] = true;
for (const auto &[e, y] : graph[x]) {
if (visited[y])
continue;
((e <= t) ? queues[t] : queues[e]).push(y);
}
}
return maximum;
}
int findEarliestTime(const int source) {
for (int i = 1; i <= n; ++i)
visited[i] = false;
const int maximum = max(findEarliestTime(source, graph), findEarliestTime(source, reversedGraph));
for (int i = 1; i <= n; ++i)
if (!visited[i])
return -1;
return maximum;
}
void determineWhen() {
for (int x = 1; x <= n; ++x)
cout << findEarliestTime(x) << ' ';
cout << '\n';
}
int main() {
#ifdef LOCAL
freopen("input.INP", "r", stdin);
#endif // LOCAL
cin.tie(0) -> sync_with_stdio(0);
cout.tie(0);
input();
determineWhen();
return 0;
}
Subtask 4
Giới hạn: ~n \leq 200,000~; ~m \leq 800,000~
Ý Tưởng
- Vì dữ liệu đầu vào đảm bảo rằng các kết quả cân không mâu thuẫn với nhau, đồ thị ~G~ được dựng trước đó sẽ không chứa chu trình. Điều này đồng nghĩa với việc ~G~ là một DAG (Directed acyclic graph).
- Ta đặt ~S~ là một thứ tự Tô-pô của ~G~ và đặt ~T_x~ là vị trí của ~x~ trong thứ tự đó (~T_x~ có thể được xem như chỉ số của ~x~ sau khi ta thực hiện sắp xếp Tô-pô).
- Để miêu tả phần còn lại của ý tưởng dễ hơn, ta sẽ đánh số đỉnh đồ thị lại theo thứ tự Tô-pô (với mọi cung ~(x, y)~ trong ~G~ sau khi đã đánh số lại, ta có ~x < y~).
- Ta đặt ~R_x~ là chỉ số đỉnh nhỏ nhất mà có cung từ trực tiếp từ ~x~ đến đỉnh đó (có thể xem như ~R_x = +\infty~ nếu như ~x~ không có cung đi ra). Ta có nhận xét rằng: với mọi đỉnh ~z < x~, nếu như ~R_u \leq x~ với mọi ~z \leq u \leq x~ thì phải tồn tại ít nhất một đường đi từ ~z~ tới ~x~.
Chứng minh
Nhận xét trên có thể được chứng minh bằng cách quy nạp:- Bước cơ sở: với ~z = x - 1~
- Vì ~z < R_z~, ta có ~x - 1 < R_z \leq x~. Nói cách khác, ~R_z = x~ hay từ ~z~ đến ~x~ có một cung trực tiếp.
- Bước quy nạp: giả định nhận xét trên thỏa với mọi ~z < u \leq x~, ta cần chứng minh nhận xét trên cũng thỏa với ~z~.
- Vì ~z~ có cung trực tiếp từ nó đến ~R_z~ (theo như định nghĩa của ~R_z~) và ~R_z~ có đường đi từ nó tới ~x~ (theo như giả định và ~z < R_z \leq x~), ~z~ có đường đi từ nó tới ~x~.
- Tương tự, ta đặt ~L_x~ là chỉ số đỉnh lớn nhất mà có cung từ trực tiếp từ đỉnh đó đến ~x~ (có thể xem như ~L_x = -\infty~ nếu như không có cung đi đến ~x~). Ta có nhận xét rằng: với mọi đỉnh ~x< z~, nếu như ~x \leq L_u~ với mọi ~x \leq u \leq z~ thì phải tồn tại ít nhất một đường đi từ ~x~ tới ~z~.
Chứng minh
Nhận xét trên có thể được chứng minh bằng cách quy nạp như nhận xét trước đó:- Bước cơ sở: với ~z = x + 1~
- Vì ~L_z < z~, ta có ~x \leq L_z < x + 1~. Nói cách khác, ~L_z = x~ hay từ ~x~ đến ~z~ có một cung trực tiếp.
- Bước quy nạp: giả định nhận xét trên thỏa với mọi ~x \leq u < z~, ta cần chứng minh nhận xét trên cũng thỏa với ~z~.
- Vì ~L_z~ có cung trực tiếp từ nó đến ~z~ (theo như định nghĩa của ~L_z~) và ~L_z~ có đường đi từ ~x~ tới nó (theo như giả định và ~x \leq L_z < z~), ~z~ có đường đi từ ~x~ tới nó.
- Dựa trên hai nhận xét này, nếu ta chỉ muốn kiểm tra rằng cấp bậc của một đồng xu ~z~ (sau khi đã đánh số lại) có thể hay không thể được xác định (và đạt ~50~% số điểm của subtask 4), ta cần kiểm tra cả hai điều kiện sau có thỏa không:
- Với mọi đỉnh ~u~ có chỉ số nhỏ hơn ~z~, ~R_u \leq z~.
- Với mọi đỉnh ~u~ có chỉ số lớn hơn ~z~, ~z \leq L_u~.
- Để xác định chính xác thời điểm sớm nhất cấp bậc của một đỉnh có thể được xác định, nếu ta thực hiện kiểm tra nêu trên nhiều lần với các tập hợp lần cân khác nhau, chi phí tính sẽ quá lớn.
- Ta đặt ~C_z~ là số lượng đỉnh ~u~ thỏa mãn điều kiện nếu ta đang xét đỉnh ~z~ (~R_u \leq z~ nếu ~u < z~ hoặc ~z \leq L_u~ nếu ~z < u~). Cấp bậc của đỉnh ~z~ có thể xác định được ở thời điểm ~C_z = n - 1~ sớm nhất.
- Ta nhận thấy rằng, nếu ta bắt đầu với một đồ thị chưa có cạnh nào và thêm dần các cạnh theo thứ tự đề bài, giả sử cạnh đang xét là ~(x, y)~ thì ta sẽ chứng kiến những thay đổi này sau đây:
- ~R_x~ có thể giảm thành ~y~: Khi này, giá trị ~C_u~ tăng thêm một đơn vị với ~u~ trong đoạn từ ~y~ tới ~R_x - 1~.
- ~L_y~ có thể tăng thành ~x~: Khi này, giá trị ~C_u~ tăng thêm một đơn vị với ~u~ trong đoạn từ ~L_x + 1~ tới ~y~.
- Sau khi cập nhật các giá trị ~C_u~ sau mỗi lần thêm cạnh, giá trị ~C_u~ mà ta cần để ý cũng chính là giá trị ~C_u~ lớn nhất (bởi ~n - 1~ cũng là giá trị lớn nhất có thể của ~C_u~).
- Dựa vào những nhận xét này, ta nhận thấy ta có thể sử dụng cấu trúc dữ liệu Segment Tree với kỹ thuật Lazy Propogation để quản lý thông tin bởi:
- Ta cần thực hiện update (tăng giá trị) các đoạn khác nhau
- Ta cần tìm giá trị lớn nhất trên đoạn.
Độ Phức Tạp
- Ý tưởng nêu trên có thể được cài đặt với độ phức tạp thời gian ~O((n + m) \log n)~.
- Việc tìm thứ tự Tô-pô có thể được thực hiện trong ~O(n + m)~.
- Vì ta cần phải duyệt qua ~O(m)~ cạnh và với mỗi cạnh, ta có thể update đoạn với độ phức tạp ~O(\log n)~.
- Ngoài ra, mỗi khi cấp bậc của một đỉnh được xác định, ta phải "xóa" đỉnh đó khỏi cấu trúc dữ liệu để có thể tìm được những đỉnh khác. Ta sẽ có ~O(n)~ thao tác "xóa" như vậy và mỗi thao tác có thể có độ phức tạp ~O(\log n)~.
Code Minh Họa
Code C++ minh họa
#include <bits/stdc++.h>
using namespace std;
template<class A, class B> bool maximize(A &a, const B &b) { return (a < b) ? (a = b, true) : false; }
template<class A, class B> bool minimize(A &a, const B &b) { return (a > b) ? (a = b, true) : false; }
constexpr int MAX_N = 200'005, MAX_M = 800'005, INF = 0X3F3F3F3F, NINF = 0XC0C0C0C0;
class SegmentTree {
private:
vector<pair<int, int> > maximum;
vector<int> lazyValue;
int length;
void pushDown(const int i) {
if (lazyValue[i]) {
int j = i << 1;
maximum[j].first += lazyValue[i];
lazyValue[j] += lazyValue[i];
j |= 1;
maximum[j].first += lazyValue[i];
lazyValue[j] += lazyValue[i];
lazyValue[i] = 0;
}
}
void modify(const int q, const int value, const int i, const int l, const int r) {
if (q < l || r < q)
return;
if (l == r) {
maximum[i] = make_pair(value, r);
return;
}
const int m = l + r >> 1;
pushDown(i);
modify(q, value, i << 1, l, m);
modify(q, value, i << 1 | 1, m + 1, r);
maximum[i] = max(maximum[i << 1], maximum[i << 1 | 1]);
}
void update(const int ql, const int qr, const int value, const int i, const int l, const int r) {
if (qr < l || r < ql)
return;
if (ql <= l && r <= qr) {
maximum[i].first += value;
lazyValue[i] += value;
return;
}
const int m = l + r >> 1;
pushDown(i);
update(ql, qr, value, i << 1, l, m);
update(ql, qr, value, i << 1 | 1, m + 1, r);
maximum[i] = max(maximum[i << 1], maximum[i << 1 | 1]);
}
void build(const int i, const int l, const int r) {
if (l == r) {
maximum[i].second = l;
return;
}
const int m = l + r >> 1;
build(i << 1, l, m);
build(i << 1 | 1, m + 1, r);
}
public:
SegmentTree(int length, const int value): length(length) {
maximum.resize(length + 1 << 2, make_pair(value, -1));
lazyValue.resize(maximum.size());
build(1, 1, length);
};
void modify(const int q, const int value) {
modify(q, value, 1, 1, length);
}
void update(const int ql, const int qr, const int value) {
update(ql, qr, value, 1, 1, length);
}
pair<int, int> getTop() const {
return maximum[1];
}
};
signed position[MAX_N], degree[MAX_N], order[MAX_N];
int n, m, x[MAX_M], y[MAX_M];
vector<int> graph[MAX_N];
void input() {
cin >> n >> m;
for (int i = 1; i <= m; ++i) {
cin >> x[i] >> y[i];
graph[x[i]].push_back(y[i]);
++degree[y[i]];
}
}
void determineTopologicalOrder() {
queue<int> q;
int t = 0;
for (int u = 1; u <= n; ++u)
if (degree[u] == 0)
q.push(u);
for (; !q.empty(); q.pop()) {
const int &u = q.front();
order[position[u] = ++t] = u;
for (const auto &v : graph[u])
if ((--degree[v]) == 0)
q.push(v);
}
}
void determineTime() {
SegmentTree segmentTree(n, 0);
vector<int> result(n + 1, -1), maximum(n + 1, NINF), minimum(n + 1, INF);
for (int i = 1, u = 0, v = 0; i <= m; ++i) {
u = position[x[i]];
v = position[y[i]];
if (v <= minimum[u]) {
segmentTree.update(v, minimum[u] - 1, 1);
minimum[u] = v;
}
if (maximum[v] <= u) {
segmentTree.update(maximum[v] + 1, u, 1);
maximum[v] = u;
}
for (;;) {
const auto &[f, z] = segmentTree.getTop();
if (f < n - 1)
break;
result[order[z]] = i;
segmentTree.modify(z, NINF);
}
}
for (int i = 1; i <= n; ++i)
cout << result[i] << ' ';
cout << '\n';
}
int main() {
#ifdef LOCAL
freopen("input.INP", "r", stdin);
#endif // LOCAL
cin.tie(0) -> sync_with_stdio(0);
cout.tie(0);
input();
determineTopologicalOrder();
determineTime();
return 0;
}
unknownnaciul
o10, Tháng 2, 2026, 1:00
0
