Bài toán cái túi trên cây
Xem dạng PDFCho cây gồm ~N~ đỉnh và một số nguyên ~K~. Các đỉnh trên cây được gán một trọng số được cho bởi dãy ~a_1, a_2, a_3, \dots, a_N~, cho biết đỉnh thứ ~i~ có trọng số ~a_i~
Tìm một thành phần liên thông~^\dagger~ gồm đúng ~k~ đỉnh trên cây sao cho tổng trọng số của các đỉnh thuộc thành phần liên thông đó là lớn nhất.
~\dagger~ Một thành phần liên thông là một tập đỉnh ~S \subseteq \{1, 2, 3, \dots, N\}~ sao cho từ một đỉnh bất kỳ thuộc tập ~S~, ta có thể di chuyển đến các đỉnh còn lại khi chỉ sử dụng cạnh thuộc cây ban đầu và đi qua các đỉnh thuộc tập ~S~.
Yêu cầu: In ra tổng trọng số của thành phần liên thông tìm được
Input
Dòng đầu tiên gồm hai số nguyên ~N, K~ là kích thước của cây và kích thước thành phần liên thông cần tìm.
Dòng thứ hai gồm ~N~ số nguyên ~a_1, a_2, a_3, \dots, a_N~ (~-10^9 \leq a_i \leq 10^9~) là trọng số của các đỉnh.
Trong ~N - 1~ dòng tiếp theo, mỗi dòng chứa hai số nguyên ~u_i, v_i~ (~1 \leq u_i, v_i \leq N~ và ~u_i \neq v_i~) mô tả một cạnh của cây.
Output
- In ra một số nguyên duy nhất là tổng trọng số lớn nhất của một thành phần liên thông có đúng ~K~ đỉnh.
Scoring
| Subtask | Điểm | ~N~ | ~K~ |
|---|---|---|---|
| 1 | ~30\%~ | ~1 \leq N \leq 300~ | ~1 \leq K \leq \min(200, N)~ |
| 2 | ~30\%~ | ~1 \leq N \leq 3000~ | ~1 \leq K \leq \min(200, N)~ |
| 3 | ~40\%~ | ~1 \leq N \leq 10^5~ | ~1 \leq K \leq \min(200, N)~ |
Sample Input 1
11 6
2 5 -1 -5 10 3 4 6 2 4 5
1 2
2 3
2 8
3 4
3 5
5 6
5 7
8 9
9 10
9 11
Sample Output 1
27
Notes
Sau đây là ảnh minh họa cho test ví dụ:
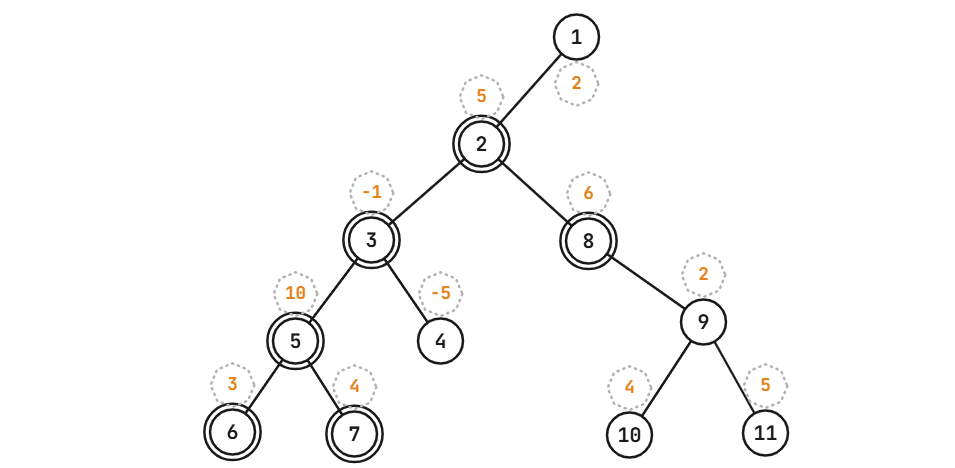
Phương án tối ưu là chọn thành phần liên thông gồm các đỉnh ~2, 3, 5, 6, 7, 8~, tổng trọng số có được là ~5 - 1 + 10 + 3 + 4 + 6 = 27~.

Bình luận