Tạp chí Tết: Tổng quan về CPU Hardware Acceleration
Author:
- Nguyễn Tấn Minh — Trường Đại học Khoa học Tự nhiên, ĐHQG-HCM.
Reviewer:
- Nguyễn Minh Nhật — Georgia Institute of Technology.
- Trần Xuân Bách — University of Chicago.
- Nguyễn Minh Hiển — Trường Đại học Công nghệ, ĐHQGHN.
Mở đầu
The things that destroy performance tend to be things that are much easier to type, such as division operations, poor cache usage, bad instruction scheduling (which is a topic by itself), and mispredicted branches.
Andrew Bromage trên nền tảng Quora
Trong lập trình thi đấu, đôi lúc chúng ta vẫn thường gặp những trường hợp "chỉ sửa code một chút thôi" nhưng từ một lời giải TLE đã trở thành lời giải AC. Ví dụ như:
- Thêm một dòng
#pragmagì đó. - Thay đổi thứ tự của một vài dòng
for. - Giảm bớt bộ nhớ của các mảng lớn hay khai báo bớt mảng.
- Thay
(a + b) % MODthànha + b - (a + b < MOD ? 0 : MOD).
Những "tối ưu" kiểu như vậy thường được các CP-ers gọi vui là ma thuật đen (hay thậm chí là... trick bẩn). Tuy nhiên, bất cứ điều gì xảy ra đều có nguyên nhân, và những trường hợp nêu trên cũng không phải ngoại lệ.
Trong bài viết này, chúng ta sẽ cùng mổ xẻ quá trình thực thi các chương trình xuống cấp độ bộ nhớ máy tính, tìm hiểu xem khi chạy những dòng code, điều gì đang thực sự diễn ra trên phần cứng, và từ đó giúp bạn đọc giải thích vì sao code lại chạy nhanh hay chậm hơn ở các trường hợp khác nhau.
Qua bài viết này, mình hy vọng bạn đọc sẽ có cái nhìn tổng quát hơn về việc phân tích tốc độ xử lý của một chương trình, bên cạnh các phương pháp tính độ phức tạp thông thường. Từ đó, những tối ưu kiểu như trên cũng không còn là những ma thuật đen nữa mà sẽ được chúng ta sử dụng một cách chủ động, hiệu quả và có ý đồ hơn.
Trong thi đấu và đặc biệt là kì thi ICPC, những "tối ưu" kiểu như vậy lại chính là ranh giới giữa việc một đội có thể giải thêm một bài (và leo lên thêm vài chục bậc trên bảng xếp hạng) hay không. Bản thân mình cũng đã trải nghiệm một trường hợp như vậy, và đó cũng chính là một trong những động lực không nhỏ đã giúp mình đưa bài viết này đến với mọi người trong Tạp chí Tết năm nay.
Sơ lược về phần cứng máy tính
Để hiểu hơn những gì đang thực sự diễn ra ở cấp độ bộ nhớ máy tính khi chúng ta chạy những dòng code, mình sẽ dành một phần của bài viết này để giới thiệu sơ lược về phần cứng máy tính cũng như cấu trúc bộ nhớ máy tính.
Phép đo tốc độ trong phần cứng máy tính
Tần số & Chu kỳ
Rõ ràng, với tốc độ xử lý của các thao tác trên máy tính, ta không thể tiến hành đo đạc bằng các loại đồng hồ đo thông thường. Do đó, người ta sử dụng một thiết bị đặc biệt có thể tạo ra dao động với tần số cực kỳ lớn và ổn định; tần số của thiết bị này thường được ghi ngay trên tên của bộ xử lý, ví dụ như 13th Gen Intel(R) Core(TM) i7-1355U (1.70 GHz).
Các lệnh máy sẽ được đo bằng đơn vị chu kỳ, tức thời gian để thiết bị này thực hiện một dao động. Với tần số ~f = 1.70~ GHz, ta có chu kỳ:
Nói cách khác, một chu kỳ chỉ xấp xỉ ~0.588~ nano-giây!
Trong bài viết này, chúng ta sẽ sử dụng chu kỳ làm đơn vị chính cho việc đánh giá các lệnh máy khác nhau.
Độ trễ và thông lượng
Để đánh giá tốc độ của các lệnh máy, ta thường sử dụng hai đại lượng thời gian sau:
- Độ trễ (latency): Đo khoảng thời gian giữa lúc bắt đầu đến khi kết thúc lệnh.
- Thông lượng (throughput): Đo khoảng thời gian giữa lúc bắt đầu đến khi có thể thực hiện lệnh cùng loại tiếp theo.
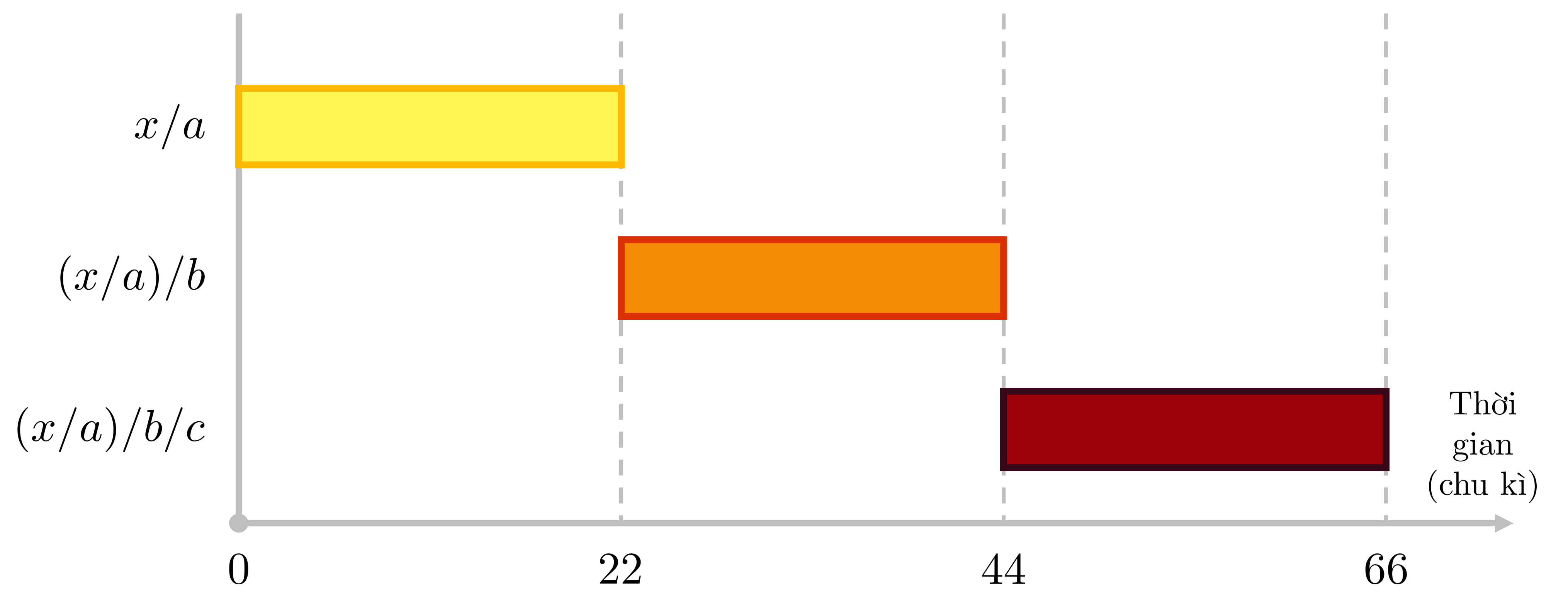
Để dễ hình dung, ta xét hai ví dụ như sau, giả sử độ trễ và thông lượng của phép chia lần lượt là ~22~ và ~8~ chu kỳ:
- Khi tính ~((x / a) / b) / c~, bắt đầu tại mốc chu kỳ ~0~, do kết quả của phép tính sau phụ thuộc vào phép tính trước nên phép tính sau sẽ được thực hiện ngay sau khi hoàn thành phép tính trước. Ta sẽ thu được kết quả của ~x / a~, ~(x / a) / b~ và ~((x / a) / b) / c~ lần lượt tại chu kỳ thứ ~22, 44, 66~.
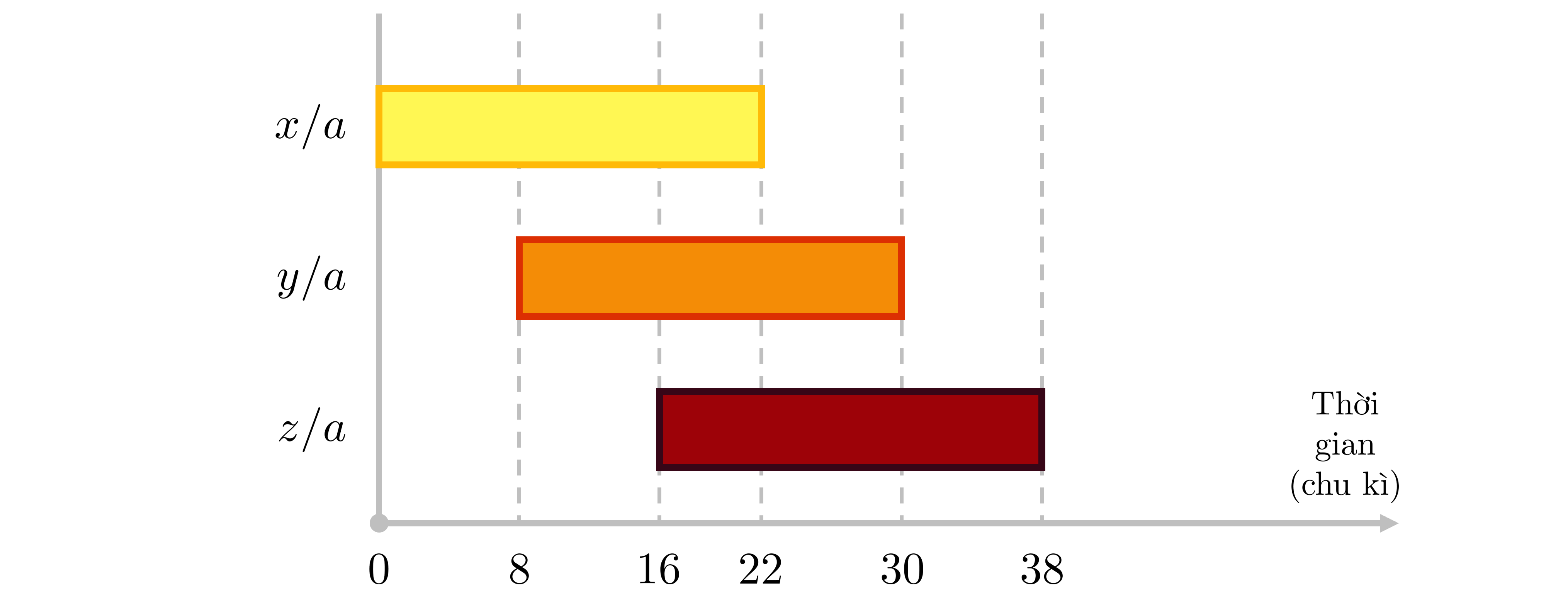
- Khi tính ~x/a~, ~y/a~ và ~z/a~, bắt đầu tại mốc chu kỳ ~0~, do kết quả của ba phép tính này độc lập với nhau, chúng sẽ được bắt đầu tại chu kỳ thứ ~0, 8, 16~. Ta sẽ thu được kết quả của ~x/a~, ~y/a~ và ~z/a~ lần lượt tại chu kỳ thứ ~22, 30, 38~.
Các loại bộ nhớ cơ bản của máy tính
Việc chúng ta sử dụng nhiều loại bộ nhớ khác nhau trong máy tính đến từ một quy luật rất tự nhiên: Bộ nhớ hỗ trợ truy cập càng nhanh thì cấu trúc vi mạch và chi phí sản xuất của nó càng cao. Do đó, trong một chiếc máy tính, ta thường tích hợp nhiều loại bộ nhớ khác nhau với những vai trò khác nhau. Các loại bộ nhớ có chi phí thấp thường được trang bị nhiều giúp ta lưu trữ được nhiều dữ liệu; các loại bộ nhớ có chi phí cao hơn thường được trang bị ít hơn và được sử dụng khi cần thực hiện tính toán nhanh.
Các loại bộ nhớ thường thấy trong một máy tính theo tốc độ truy cập giảm dần bao gồm:
- Register: Là phần bộ nhớ nằm ngay trên CPU, có khả năng thực hiện tính toán nhanh nhất. Một register trong các máy tính hiện nay thường có ~64~ bit; một nhân CPU có nhiều register (khoảng vài chục) cho các mục đích tính toán khác nhau.
- Cache (SRAM): Là phần bộ nhớ nằm rất gần CPU, đóng vai trò là phần bộ nhớ trung gian giúp tăng tốc độ truy cập dữ liệu từ main RAM. Khi cần thực hiện phép tính, các ô nhớ được quan tâm sẽ được đưa từ cache vào register, hoặc từ main RAM vào cache rồi vào register. Ta sẽ tìm hiểu cơ chế này ở phần sau.
- Main RAM (DRAM): Là phần bộ nhớ chứa các thông tin đang được hệ điều hành xử lý khi chạy các chương trình trên máy tính hay các biến trung gian phát sinh. Giới hạn bộ nhớ của main RAM hiện nay rất đa dạng và tùy thuộc vào từng dòng máy tính, có thể dao động từ ~8~ GB đến hơn ~128~ GB. Khi cần thực hiện phép tính, các ô nhớ cần quan tâm sẽ được đưa từ main RAM vào cache rồi vào register.
- Secondary storage: Là phần bộ nhớ chủ yếu được sử dụng để lưu trữ như ổ đĩa cứng, bộ nhớ đám mây,... Khác với 2 loại RAM ở trên, phần bộ nhớ này sẽ không bị mất thông tin khi máy tính không được cung cấp điện. Với cấu trúc vi mạch cực kỳ đơn giản, phần bộ nhớ này có thể lưu trữ lượng thông tin lên đến nhiều TB. Khi một chương trình được khởi động, các ô nhớ tương ứng sẽ được đưa từ Secondary storage vào main RAM.
Để dễ hình dung sự khác biệt về kích thước và tốc độ truy cập của từng loại bộ nhớ, chúng ta sẽ tìm hiểu số liệu dựa trên một máy tính cá nhân qua bảng dưới. Lưu ý rằng thời gian truy cập chỉ mang tính tương đối vì thời gian thực tế phụ thuộc vào rất nhiều yếu tố khác nhau.
| Phần bộ nhớ | Giới hạn bộ nhớ trong 1 nhân | Thời gian truy cập (chu kì) | Thời gian truy cập (giây, tần suất 1.7 GHz) |
|---|---|---|---|
| Register | ~64~ bit ~\times~ số register | Không đáng kể | Không đáng kể |
| L1 cache | ~80~ KB (performance) / ~96~ KB (efficiency) | ~3~ chu kì | ~1.76~ nano-giây |
| L2 cache | ~1280~ KB (performance) / ~2048~ KB cho 4 nhân dùng chung (efficiency) | ~9~ chu kì | ~5.29~ nano-giây |
| L3 cache | ~12~ MB cho tất cả các nhân dùng chung | ~43~ chu kì | ~25.28~ nano-giây |
| Main RAM | ~8~ đến ~16~ GB | ~400~ chu kì | ~235.20~ nano-giây |
| Local Disk (SSD) | ~256~ GB đến ~2~ TB | hơn ~3 \cdot 10^5~ chu kì | hơn ~170~ micro-giây |
Lưu ý, có hai loại nhân là performance core và efficiency core phục vụ hai mục đích khác nhau. Do đó, cấu trúc bộ nhớ trong hai loại nhân này cũng là khác nhau.
Trong lập trình thi đấu, ta thường sử dụng giới hạn ~10^8~ hay ~2 \cdot 10^8~ như một mức ước lượng "an toàn" về số thao tác tính toán ta có thể thực hiện trong ~1~ giây. Như vậy, ta đang giả sử một phép tính trung bình mất ~5~ đến ~10~ nano-giây -- một con số tương đối phù hợp với các dòng máy hiện hành.
Cache
Có thể thấy từ số liệu trên, tốc độ truy cập và tính toán của register là nhanh hơn rất nhiều (khoảng 300 lần) so với RAM. Nếu việc lấy dữ liệu để tính toán được diễn ra trực tiếp trên RAM, ta có thể thấy đây là một sự lãng phí vô cùng lớn. Cache được tạo ra để giải quyết vấn đề này, khi register yêu cầu một vùng nhớ để thực hiện tính toán, một trong hai điều sau sẽ xảy ra:
- Nếu vùng nhớ mà register cần gọi đã có sẵn trong cache, máy tính chỉ việc lấy thông tin từ phần bộ nhớ này. Ta gọi đây là cache hit.
- Nếu vùng nhớ mà register cần gọi chưa có trong cache, máy tính quay về main RAM và lấy một Cache Line (tức ~64~ bytes) ghi đè lên một vùng nhớ nào đó trong cache theo một chiến lược nhất định. Ta gọi đây là cache miss.
Trong các máy tính hiện nay, cache thường được chia ra thành nhiều lớp trung gian gọi là L1, L2, L3,... nhằm tối ưu hơn nữa quá trình vận chuyển thông tin từ main RAM sang register.
Đến đây, bạn đọc cũng có thể nhận ra, cụm từ cache-friendly coding chính là việc viết code giúp máy tính hạn chế cache miss một cách tối đa.
Lệnh máy (CPU instruction)
Để thực hiện các phép tính, phép gán, biến đổi,... tất cả các code khi chạy sẽ được biến thành lệnh máy (CPU instruction). Tùy vào mỗi dòng sản phẩm CPU và các lệnh khác nhau, hiệu suất thu được cũng là khác nhau. Để đánh giá các lệnh máy cơ bản trên bộ xử lý 13th Gen Intel(R) Core(TM) i7-1355U (1.70 GHz) (thuộc dòng Alder Lake), ta phân tích hai đại lượng là độ trễ và thông lượng qua bảng sau số liệu sau:
| Lệnh | Độ trễ (Alder Lake-P) | Thông lượng (Alder Lake-P) | Độ trễ (Alder Lake-E) | Thông lượng (Alder Lake-E) |
|---|---|---|---|---|
Phép cộng cơ bản (VPADDQ) |
1 | 0.33 | 2 | 0.67 |
Phép nhân cơ bản (VMULPD) |
4 | 0.5 | 6 | 0.5 |
Phép truy cập bộ nhớ cơ bản (VMOVDQA) |
4; 12 | 0.5 | 7; 11 | 1.0 |
Phép chia cơ bản (VDIVPD) |
13; 22 | 8.0 | 30; 33 | 32.0 |
Số liệu cụ thể được tham khảo tại đây và được đo theo đơn vị chu kì trên tần số 1.70 GHz.
Lưu ý, một số thao tác có đến hai giá trị cho độ trễ, lý do là vì ta xét tốc độ của thao tác trong các hoàn cảnh khác nhau.
Khi tính toán độ phức tạp, ta xem cả 4 thao tác trên có cùng độ phức tạp ~\mathcal{O}(1)~. Tuy nhiên, không khó để nhận ra rằng với cùng số thao tác, các loại lệnh máy khác nhau có thể cho ra chênh lệch về tốc độ một cách đáng kể.
Sơ lược về benchmarking
Đối với các code đơn giản như vòng lặp và gán đơn thuần, đôi khi, việc so sánh thời gian sẽ không được diễn ra một cách công bằng do trình biên dịch của C++ sẽ tối ưu bằng cách lược bỏ các dòng code không "hữu ích".
Để "ép" trình biên dịch C++ biên dịch toàn bộ đoạn code cần so sánh để mô phỏng các đoạn code thực tế, ta cần sử dụng một thư viện benchmarking đặc biệt. Trong bài viết này, mình sẽ sử dụng Google Benchmark – một thư viện benchmarking nổi tiếng dành cho C++.
Bạn đọc có thể cài đặt CMake và Google Benchmark theo hướng dẫn tại Github repository của thư viện này. Ngoài ra, bạn đọc cũng có thể tham khảo hướng dẫn sử dụng thư viện nếu muốn tự chạy lại các benchmark trong bài viết này. Do việc cài đặt và setup CMake cũng tương đối phức tạp, bạn đọc có thể tham khảo thêm các nguồn tài liệu sẵn có trên internet.
Ngoài ra, các benchmark trong bài viết này sẽ được chạy bằng bộ xử lý 13th Gen Intel(R) Core(TM) i7-1355U (1.70 GHz) trên máy tính cá nhân. Bạn đọc có thể tham khảo toàn bộ code được sử dụng để benchmark trong bài viết này ở phần Phụ lục ở cuối bài viết.
Cache-friendly coding
Như vậy, qua phần phân tích cấu trúc bộ nhớ máy tính, câu hỏi về việc vì sao cùng một thuật toán, nhưng hai cách cài đặt khác nhau lại có thể cho ra hai thời gian chạy rất khác nhau cũng đã phần nào được giải đáp -- có thể lý giải rằng chương trình chậm hơn đã gây ra nhiều cache miss hơn trong quá trình cài đặt.
Câu hỏi đặt ra bây giờ là: Khi cài đặt, ta cần lưu ý điều gì để code của chúng ta luôn cho ra "chương trình nhanh hơn" trong câu chuyện nêu trên?
Cục bộ hóa
Cục bộ hóa khi duyệt mảng
Tất nhiên, chiến lược caching của máy tính không thể quá cầu kì và phức tạp được. Máy tính sẽ có xu hướng cache một vùng nhớ liên tục trong main RAM. Đây là một lưu ý cực kỳ quan trọng đối với các lập trình viên khi xử lý mảng.
Ta sẽ thử nghiệm hai kiểu duyệt mảng (tuần tự và ngẫu nhiên), sau đó sử dụng Google Benchmark để so sánh hai kiểu duyệt trên các kích thước mảng khác nhau.
Kết quả benchmark cho ~N = 2^k~ với ~k \in [4; 24]~ như sau:
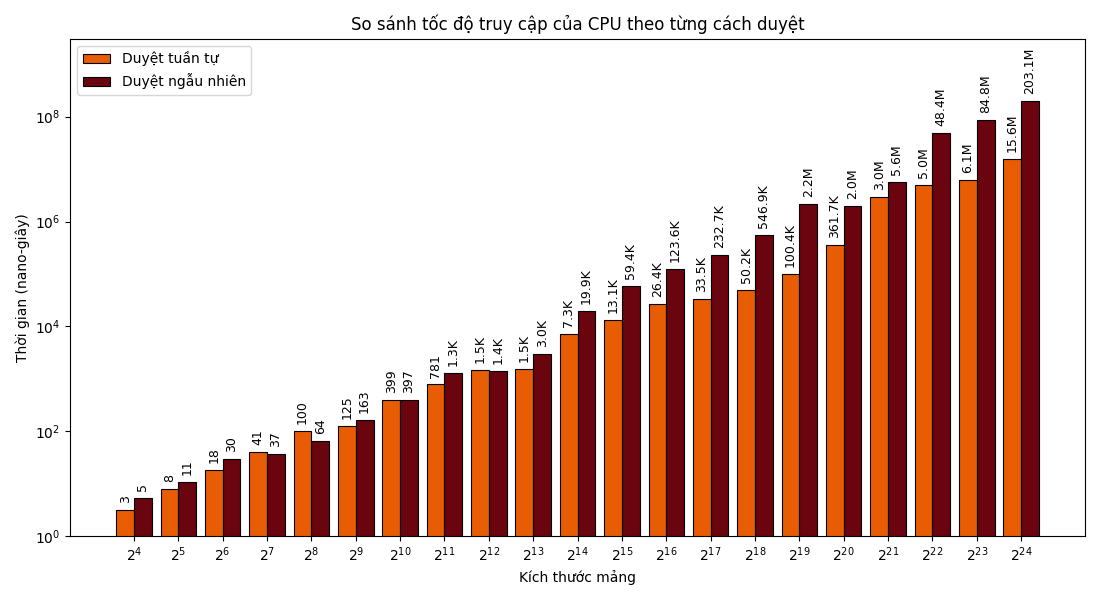
Bạn đọc lưu ý rằng trục ~y~ được thể hiện bằng thang ~\log~ với cơ số ~10~, do đó, độ cao của các cột chỉ mang tính tương đối.
Có thể thấy, kể từ mốc ~N = 2^{16} \approx 7 \cdot 10^4~, tốc độ của cách duyệt tuần tự đã là nhanh gấp 3 lần cách duyệt ngẫu nhiên. Ta có thể lý giải điều này là do cách duyệt ngẫu nhiên gây ra quá nhiều cache miss khi ~N~ đủ lớn; mặt khác, với các kích thước ~N \leq 2^{12}~, ta chưa thấy khác biệt rõ rệt là vì kích thước các cache L1, L2, L3 đủ lớn để gần như chứa cả mảng.
Cục bộ hóa khi khai báo bộ nhớ
Khi tự thiết kế các cấu trúc dữ liệu, hoặc sử dụng các cấu trúc dữ liệu thuộc thư viện chuẩn của C++, chúng ta cùng cần lưu ý đến tính phân mảnh (fragmentation) của bộ nhớ. Nói cách khác, ta cần quan tâm đến việc bộ nhớ của cấu trúc dữ liệu sẽ được lưu trong một dải các ô nhớ liên tiếp trong RAM (phân mảnh thấp) hay những ô nhớ rời rạc xa nhau (phân mảnh cao).
Ví dụ, các cấu trúc dữ liệu sau đây có tính phân mảnh thấp, phù hợp với cache-friendly coding:
| Cấu trúc dữ liệu | Giải thích |
|---|---|
|
Mảng (nhiều chiều), vector một chiều |
Mảng (nhiều chiều) và vector một chiều được lưu trữ dưới dạng một dải bộ nhớ liên tục trong RAM, từ đó, việc caching trên mảng và vector cũng được diễn ra thuận tiện hơn. |
| Hàng đợi ưu tiên |
Vì cơ chế hoạt động của hàng đợi ưu tiên cho phép đánh số các nút trên cây nhị phân và lưu trữ chúng dưới dạng mảng, container được sử dụng mặc định là vector nên việc tổ chức bộ nhớ cũng cache-friendly tương tự vector.
|
Bitset và vector chứa kiểu dữ liệu bool
|
Bitset là một cấu trúc dữ liệu cực kì cache-friendly vì dữ liệu được tổ chức một cách rất dày đặc (1 phần tử chiếm đúng 1 bit), vector<bool> là một trường hợp đặc biệt của vector và cũng có cơ chế lưu trữ tương tự. Lưu ý rằng bitset và vector<bool> hiệu quả hơn mảng về mặt lưu trữ vì một giá trị bool thông thường chiếm 1 byte (8 bit).
|
Mặt khác, các cấu trúc dữ liệu sau đây có tính phân mảnh trung bình/cao:
| Cấu trúc dữ liệu | Giải thích |
|---|---|
| Vector nhiều chiều | Một vector ~d~ (với ~d \geq 2~) chiều lại được lưu trữ dưới dạng một dải bộ nhớ liên tục, mỗi ô nhớ lại là một con trỏ, trỏ đến một vector ~d - 1~ chiều khác. Ví dụ, nếu chỉ thao tác trên các ô thuộc một dòng của vector 2 chiều, CPU vẫn có thể thực hiện caching hiệu quả; nhưng nếu thao tác trên các dòng khác nhau, tính cục bộ sẽ không còn được đảm bảo do bộ nhớ của các dòng có thể được lưu trữ ở các vị trí rời rạc trên RAM. |
|
Hàng đợi hai đầu, stack, queue |
Hàng đợi hai đầu có tính phân mảnh trung bình vì dữ liệu được lưu dưới dạng các block rời rạc. Một điều bất ngờ là stack và queue đều sử dụng container mặc định là deque nên điều tương tự cũng xảy ra với 2 cấu trúc dữ liệu này.
|
|
Danh sách liên kết đơn, danh sách liên kết đôi, set, map |
Các cấu trúc dữ liệu dựa trên node (node-based data structures) có tính phân mảnh rất cao vì các phần tử được khai báo một cách rời rạc.
|
Để so sánh tốc độ chạy của một số cấu trúc dữ liệu nêu trên, mình thực hiện benchmark thời gian thực hiện ~10^9~ thao tác duyệt trên mảng, hàng đợi hai đầu và danh sách liên kết đơn. Kết quả như sau:
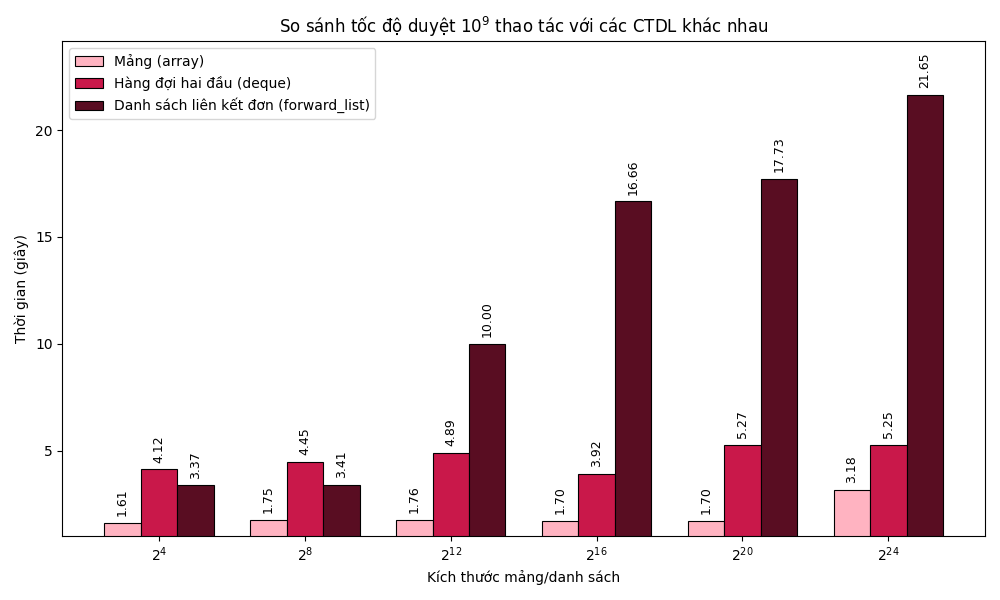
Có thể thấy, chênh lệch về hiệu suất của mảng/vector so với hàng đợi hai đầu là không quá lớn, do các ô nhớ của hàng đợi hai đầu vốn không quá phân mảnh. Tuy nhiên, danh sách liên kết đơn lại có tốc độ duyệt cực kì chậm khi số phần tử tăng cao, điều này là do các phần tử của danh sách liên kết đơn được lưu trữ rải rác trong RAM, khiến việc cục bộ hóa trở nên khó khăn.
Tất nhiên, những cấu trúc dữ liệu nêu trên, dù cho có cache-friendly hay không, đều có những ưu điểm riêng của nó. Tùy vào nhu cầu sử dụng trong từng trường hợp, ta chọn những cấu trúc dữ liệu khác nhau.
Tối ưu bộ nhớ
Trong rất nhiều trường hợp, khi cố gắng tối ưu bộ nhớ, ta cũng vô tình tối ưu thời gian chạy của thuật toán, dù trên lý thuyết, số thao tác duyệt không thay đổi. Qua số liệu benchmark ở phần trước, ta cũng thấy rằng, cùng là duyệt ~10^9~ thao tác trên cùng một loại cấu trúc dữ liệu, việc tăng/giảm kích thước của cấu trúc dữ liệu đó cũng ảnh hưởng nhiều đến tốc độ cuối cùng.
Điều này có thể được giải thích như sau: khi sử dụng càng ít bộ nhớ, vùng nhớ được đưa vào 1 trong 3 cache sẽ có xu hướng chiếm một phần lớn hơn của vùng nhớ cần thao tác; hơn nữa, khi random-access với vùng nhớ nhỏ, ta sẽ có xác suất truy cập lại vào các vùng nhớ cũ vẫn còn nằm ở trong cache, từ đó tăng số lần cache hit hơn.
Sau đây là một biểu đồ thể hiện số megabytes mà CPU có thể thực hiện random-access trong ~1~ giây trên một mảng gồm ~N = 2^k~ (với ~k \in [2; 22]~) phần tử:
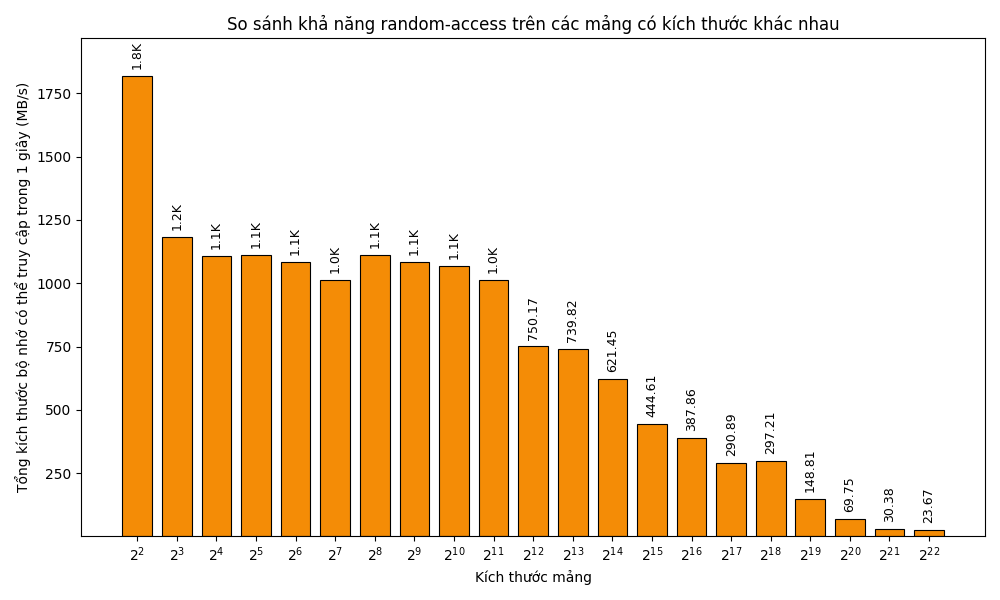
Có thể thấy, tốc độ truy cập khá tương đồng ở nhóm ~N \in [2^3; 2^{11}]~ do toàn bộ dữ liệu đều được đưa vào L1 cache. Ở các kích thước lớn hơn, tỉ lệ cache hit giảm dần kéo theo tốc độ truy cập cũng giảm mạnh.
Khử đệ quy
Trong các tài liệu lập trình nói chung, ta vẫn thường được nghe đến cụm từ "khử đệ quy". Thật vậy, trong những trường hợp có thể thay thế đệ quy thành vòng lặp, chúng ta nên sử dụng vòng lặp vì cơ chế sử dụng bộ nhớ của hai cách cài đặt rất khác nhau và từ đó tạo ra một khác biệt đáng kể về tốc độ và bộ nhớ.
Cơ chế tổ chức bộ nhớ trong hàm đệ quy
Khi dùng hàm đệ quy, với mỗi lần gọi hàm, chương trình sẽ khai báo một stack frame dùng để lưu trữ các tham số, biến trung gian,... Ví dụ, với hàm đệ quy sau:
void iterate (int node = 1, int depth = 1) { // Hàm duyệt cây nhị phân
if (depth == 3) return;
iterate(node * 2, depth + 1); // duyệt cây con trái
iterate(node * 2 + 1, depth + 1); // duyệt cây con phải
}
Khi duyệt đến nút số ~6~ ở tầng thứ ~3~, bộ nhớ stack đang phải lưu trữ bộ nhớ của cả ba lần gọi đệ quy chưa hoàn thành là ~\texttt{iterate}(1, 1)~, ~\texttt{iterate}(3, 2)~ và ~\texttt{iterate}(6, 3)~.
Như vậy, lượng bộ nhớ cần dùng là tích của độ sâu đệ quy và kích thước của một stack frame. Mặt khác, khi dùng vòng lặp, độ phức tạp bộ nhớ chỉ sẽ bằng độ phức tạp bộ nhớ của phần nằm bên trong vòng lặp.
Ví dụ, cả hai hàm sau đều có mục đích tương đương, nhưng hàm đệ quy có độ phức tạp bộ nhớ tuyến tính còn hàm sử dụng vòng lặp có độ phức tạp hằng số.
void recursiveFunction (int n, int i = 0) {
if (i + 1 < n) recursiveFunction(n, i + 1);
// ...
}
void iterativeFunction (int n) {
for (int i = 0; i < n; i++) {
// ...
}
}
Bất lợi của hàm đệ quy
Với cơ chế hoạt động của đệ quy so với vòng lặp, ta có thể thấy một số nguyên nhân khiến đệ quy hoạt động kém hiệu quả hơn như sau:
- Gọi hàm nhiều lần: Đối với các hàm thông thường, thời gian được sử dụng cho việc gọi hàm là cực kì ít so với phần còn lại của code. Tuy nhiên, khi phải gọi hàm nhiều lần như khi làm việc với hàm đệ quy, thời gian gọi hàm cũng đóng góp một lượng thời gian đáng kể vào tốc độ chạy của chương trình, bạn đọc có thể tham khảo thêm về cơ chế gọi hàm tại đây.
- Cache miss: Từ việc sử dụng nhiều bộ nhớ hơn một cách đáng kể, ta dễ thấy rằng hàm đệ quy dễ gây ra cache miss hơn nhiều so với vòng lặp.
- Một lý do khác khiến đệ quy chậm hơn vòng lặp mà ta không đào sâu trong khuôn khổ bài viết này là branching.
Ngoài ra, người ta thường khử đệ quy là vì bộ nhớ của đệ quy được khai báo trên bộ nhớ stack, vùng bộ nhớ này vốn có giới hạn nhỏ.
Tuy nhiên, như đã đề cập, đó là trong những trường hợp ta có thể thay thế đệ quy bằng vòng lặp. Trong lập trình nói chung, đệ quy vẫn là một công cụ cực kỳ mạnh mẽ và hữu ích trong nhiều trường hợp cụ thể.
Ứng dụng trong lập trình thi đấu
Quy hoạch động nhiều chiều
Sử dụng cài đặt bottom-up khi có thể
Khi tìm hiểu Quy hoạch động cơ bản, ta vẫn thường được nghe đến hai cách cài đặt bottom-up và top-down. Tuy cả hai cách trông có vẻ như sẽ cho kết quả giống nhau, nhưng điểm khác biệt lại nằm ở chỗ cách cài đặt bottom-up sử dụng vòng lặp và cách còn lại sử dụng hàm đệ quy.
Do đó, trong những trường hợp mà thứ tự duyệt trạng thái Quy hoạch động đơn giản là duyệt một biến từ bé đến lớn (hoặc ngược lại), cách cài đặt bottom-up sẽ là lựa chọn mang lại hiệu quả về thời gian chạy vượt trội so với cách cài đặt còn lại. Ta chỉ thường sử dụng top-down trong những trường hợp mà việc xác định thứ tự duyệt các trạng thái là phức tạp như DAG, vì bản chất việc sử dụng DFS để xác định thứ tự topo và hàm Quy hoạch động sử dụng đệ quy là tương đương nhau.
Giảm chiều Quy hoạch động
Đối với các dạng Quy hoạch động mà khoảng cách giữa các tham số truy hồi trong cùng một chiều là không quá lớn, ta hoàn toàn có thể rút bớt số chiều Quy hoạch động xuống để tiết kiệm bộ nhớ. Ví dụ, với công thức truy hồi cho bài toán Quy hoạch động cái túi (bỏ qua các trường hợp biên):
Ta thấy rằng để tính bất kì giá trị nào trên dòng ~i~ trên bảng Quy hoạch động, ta chỉ cần xét đến các giá trị trên dòng ngay trên nó (tức dòng ~i - 1~); hơn nữa, kết quả cuối cùng mà ta quan tâm chỉ là các giá trị nằm trên dòng thứ ~n~. Từ đó, ta có thể chỉ duy trì hai dòng liên tiếp của bảng Quy hoạch động. Dòng thứ ~i~ trên công thức định nghĩa bây giờ sẽ được lưu trên dòng thứ ~i \bmod 2~ trên bảng Quy hoạch động, và dòng ~i - 1~ trên công thức ứng với dòng ~(i - 1) \bmod 2~ của bảng.
Thậm chí, với đặc điểm của thuật toán Quy hoạch động cái túi, ta có thể giảm bộ nhớ xuống còn đúng 1 dòng, tức chỉ dùng mảng 1 chiều gồm ~C~ phần tử!
Tổng quát hơn, nếu hàm Quy hoạch động ~\texttt{solve}(i, \dots)~ chỉ truy hồi đến một giá trị ~\texttt{solve}(i - d, \dots)~ nào đó với ~d~ là một hằng số đủ nhỏ, ta hoàn toàn có thể chỉ quan tâm ~d + 1~ dòng liên tiếp của bảng Quy hoạch động.
Lưu ý rằng cách làm trên vẫn giữ nguyên độ phức tạp thời gian của Quy hoạch động cái túi là ~\mathcal{O}(nC)~, tuy nhiên, bộ nhớ bây giờ đã được giảm xuống ~\mathcal{O}(C)~ -- cực kỳ có lợi cho việc caching vùng bộ nhớ được sử dụng cho Quy hoạch động.
So sánh
Để so sánh, mình sẽ giải bài tập Knapsack 1 thuộc AtCoder Educational DP Contest trên nền tảng VNOJ bằng 3 lời giải khác nhau. Kết quả so sánh như sau:
| Tiêu chí đánh giá | Top-down | Bottom-up, bộ nhớ ~\mathcal{O}(nC)~, duyệt ~i~ trước | Bottom-up, bộ nhớ ~\mathcal{O}(C)~ |
|---|---|---|---|
| Thời gian | ~0,538~ giây | ~0,106~ giây | ~0,012~ giây |
| Bộ nhớ | ~89,88~ MB | ~80,19~ MB | ~3,95~ MB |
Lưu ý, nền tảng VNOJ chỉ cho phép xem bài nộp của người dùng khác khi bạn đã giải được bài tập đó. Bạn đọc có thể tham khảo bài viết về Quy hoạch động cái túi ở nền tảng VNOI Wiki.
Nhân ma trận
Nhắc lại, phép nhân ma trận ~\mathbf{A} \times \mathbf{B}~ (với kích thước của ~\mathbf{A}, \mathbf{B}~ lần lượt là ~n \times m~ và ~m \times q~) cho ra ma trận ~\mathbf{C}~ có kích thước ~n \times q~ được định nghĩa theo công thức:
Trong bài viết này, ta sẽ xét bài toán nhân ma trận có modulo -- dạng nhân ma trận thường gặp trong lập trình thi đấu. Nói cách khác, ta cần trả về ma trận ~\mathbf{C}~ có giá trị đã được chia lấy dư cho một modulo ~M~ cho trước. Trong các code được dùng trong bài viết này, mình sử dụng ~M = 998 \space 244 \space 353~.
Sử dụng ma trận chuyển vị
Đối với các mảng hai chiều, bộ nhớ thường được trải phẳng theo dòng, nói cách khác, các phần tử thuộc cùng một dòng sẽ được tổ chức thành một đoạn liên tiếp trên mảng trải phẳng. Do đó, trên các ma trận lớn, ta thường ưu tiên duyệt dòng rồi cột hơn là cột rồi dòng trên mảng hai chiều.
Ta thấy rằng khi thực hiện phép tích chập để tính ~\mathbf{C}_{i, j}~, ta đang duyệt các phần tử trên dòng thứ ~i~ của ~\mathbf{A}~ (cache-friendly), nhưng lại duyệt các phần tử trên cột ~j~ của ~\mathbf{B}~ (cache-unfriendly).
Để khắc phục điều này, ta có thể tính trước ma trận ~\mathbf{B}^\intercal~ (với ~\mathbf{B}^\intercal_{i, j} = \mathbf{B}_{j, i}~) để có thể duyệt các phần tử trên dòng thứ ~j~ của ~\mathbf{B}^\intercal~. Công thức nhân ma trận trở thành:
Phương pháp phân khối (tiling)
Có thể thấy, phép nhân ma trận thông thường gặp phải 2 vấn đề khiến tốc độ thực hiện trở nên chậm:
- Không có tính cục bộ cao nên caching không tốt.
- Sử dụng đúng ~n \times m \times q~ thao tác modulo -- một điểm trừ cực kỳ lớn của nhân ma trận có modulo.
Trong phần này, ta sẽ tìm hiểu phương pháp phân khối -- một phương pháp nhân ma trận khắc phục được hai điểm yếu trên tương đối tốt.
Trước tiên, ta dựa vào nhận xét rằng với các ma trận nhỏ, cho dù có duyệt các phần tử theo thứ tự nào, tốc độ nhân ma trận vẫn thường rất nhanh. Ta có thể lý giải đơn giản là kích thước của cả ba ma trận ~\mathbf{A}, \mathbf{B}, \mathbf{C}~ đủ nhỏ để lưu trữ trong L1 cache.
Bây giờ, ta chia nhỏ một phép nhân ma trận vuông ~8 \times 8~ thành các phép nhân ma trận nhỏ ~2 \times 2~. Ví dụ, để tính giá trị của một ma trận con ~2 \times 2~ nằm ở góc trên trái của ~\mathbf{C}~, ta thực hiện 4 bước nhân ma trận ~2 \times 2~ như sau:
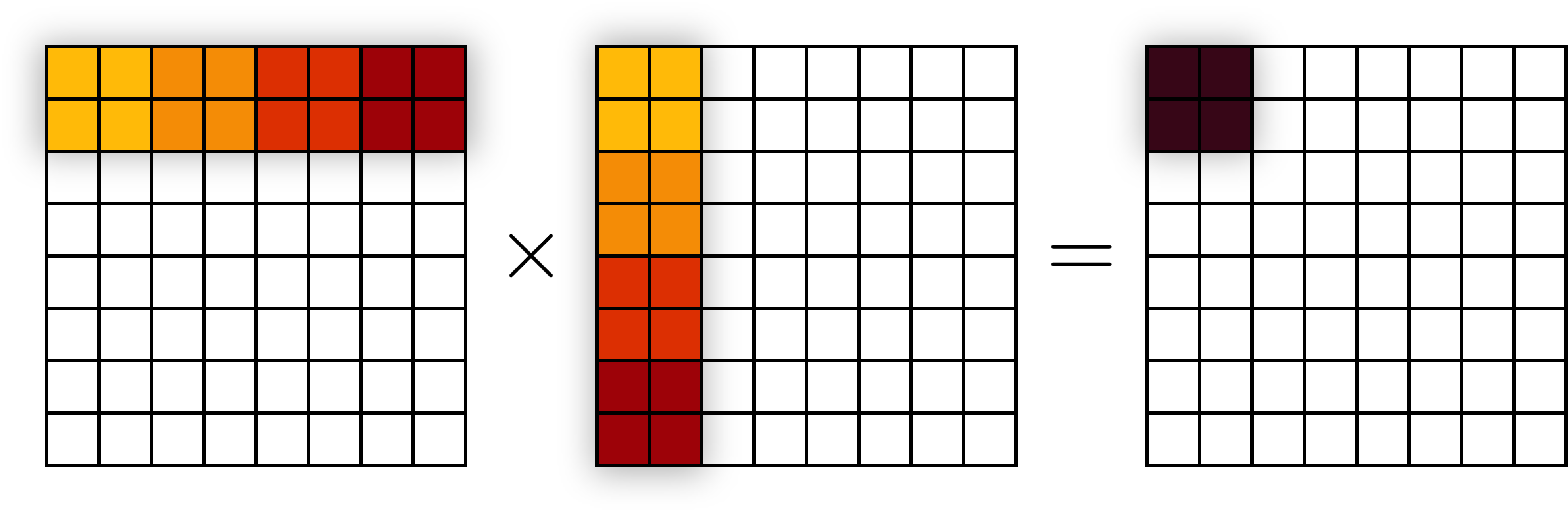
Lưu ý, các ô có cùng màu sẽ được thực hiện trong cùng một lần nhân ma trận.
Do kích thước của ba ma trận con ~2 \times 2~ là đủ nhỏ để chứa trong L1 cache và truy cập nhanh, ta xem như chi phí truy cập một phần tử nào đó chỉ bằng lần truy cập đầu tiên trong bước nhân ma trận ~2 \times 2~ tương ứng. Dễ thấy, để thực hiện phép nhân ma trận trên cả ma trận ~8 \times 8~, ta cần thực hiện ~\left( \frac{8}{2} \right)^3 = 64~ bước, mỗi bước thực hiện tốn ~3 \times 2^2 = 12~ lần đưa bộ nhớ vào L1 cache. Như vậy, tổng số lần truy cập bộ nhớ ngoài L1 cache là ~64 \times 12 = 768~, nhỏ hơn tổng số bước truy cập dữ liệu trong nhân ma trận thông thường là ~3 \times 8^3 = 1536~ gấp hai lần.
Tổng quát hơn, nếu kích thước của ma trận con là ~B \times B~ và kích thước của ma trận lớn là ~N \times N~ thì ta cần ~\frac{3N^3}{B}~ lần truy cập bộ nhớ ngoài L1 cache, tức ít hơn gấp ~B~ lần so với tổng số bước truy cập dữ liệu trong nhân ma trận thông thường.
Lưu ý, đây vẫn chỉ là một phép ước lượng khi bỏ qua chi phí truy cập các ô nhớ đã nằm trong L1 cache và bỏ qua những tối ưu khác trong quá trình truy cập dữ liệu của CPU; trên thực tế, cả hai cách tiếp cận đều cần truy cập bộ nhớ đúng ~3N^3~ lần. Nói cách khác, cách làm này không giúp giảm số lần truy cập bộ nhớ mà làm cho mỗi lần truy cập bộ nhớ được tối ưu hơn.
Ta cần chọn một giá trị ~B~ vừa đủ lớn vừa đảm bảo cả ba ma trận con ~B \times B~ đều có thể nằm vừa trong L1 hoặc L2 cache. Trên thực tế, giá trị ~B~ thường dùng cho phương pháp phân khối khi nhân ma trận là ~B = 16~ hay ~B = 32~, đủ để chứa cả ba ma trận con có mỗi phần tử chiếm ~8~ bytes (như long long hay double trong C++) trong một L1 cache thông thường có kích thước ~32~ KB.
Hơn nữa, với ~B = 16~, ta thấy rằng ~M^2 \cdot B < 2^{64}~ vẫn không gây tràn số trên số nguyên ~64~-bit, với các giá trị ~M \approx 10^9~ thường gặp trong lập trình thi đấu. Như vậy, ta chỉ cần thực hiện modulo sau khi đã thực hiện xong mỗi phép tích chập.
Có thể thấy, ta đã xử lý một lúc hai trở ngại thời gian lớn nhất được nêu trên trong phép nhân ma trận.
Ở phần cài đặt (xem phần Phụ lục ở dưới), mình thực hiện thêm một tối ưu nhỏ bằng cách chuyển vị ma trận ~\mathbf{B}~ ngay khi trích xuất ma trận con của nó. Trên nền tảng Library Checker, cách cài đặt của mình thực hiện được phép nhân ma trận ~1024 \times 1024~ trong dưới ~400~ mili-giây.
So sánh
Để so sánh hai cách tối ưu nêu trên, mình sẽ thực hiện benchmark cả 3 cách nhân ma trận trên ma trận vuông có độ dài cạnh ~N \in 2^k~ (với ~k \in [1; 10]~). Lưu ý, ma trận được sử dụng trong phần cài đặt là ma trận đã được trải phẳng thành vector 1 chiều nhằm tối ưu cache.
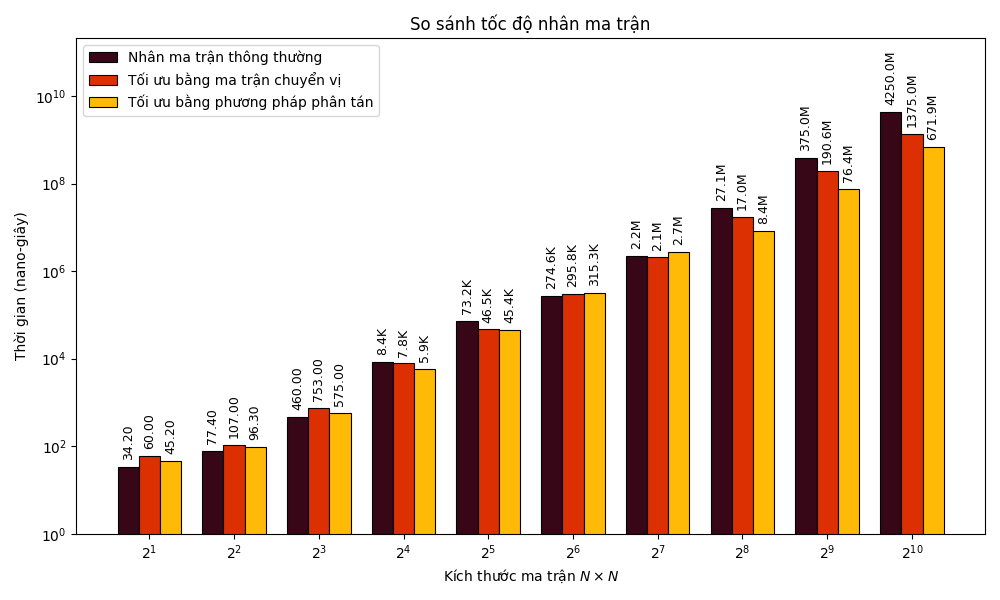
Bạn đọc lưu ý rằng trục ~y~ được thể hiện bằng thang ~\log~ với cơ số ~10~, do đó, độ cao của các cột chỉ mang tính tương đối.
Ngoài ra, bạn đọc có thể tham khảo animation sau được thực hiện bởi Jukka Suomela, so sánh phương pháp phân khối (bên phải ngoài cùng) với các phương pháp nhân ma trận khác.
Pragma
Một chi tiết được chú ý và bàn luận nhiều trên các nền tảng mạng xã hội về đề thi Học sinh giỏi Quốc gia môn Tin học năm nay (năm học 2025-2026) là dòng ghi chú ở đầu đề bài ở cả hai ngày thi như sau:

Trước khi tìm hiểu lý do dòng ghi chú này lại xuất hiện trong đề thi Học sinh giỏi Quốc gia, ta cùng tìm hiểu sơ lược về định hướng biên dịch chương trình (hay từ khóa pragma) và ứng dụng của nó trong lập trình C++.
Sơ lược về pragma
Từ khóa pragma là những chỉ thị đặc biệt dành cho trình biên dịch nhằm làm thay đổi một số hành vi của chương trình khi biên dịch chương trình. Từ khóa này thường được sử dụng kèm với các chỉ thị như once hay GCC poison hay GCC target và thường đi kèm các từ khóa như O2, unroll-loops, avx2,... tùy vào chỉ thị được dùng. Ta có thể sử dụng một lúc nhiều từ khóa như sau:
#pragma GCC optimize("O3", "unroll-loops")
Nếu muốn sử dụng chỉ thị cho đúng một hàm của chương trình, ta có thể sử dụng thêm từ khóa __attribute__, ví dụ:
__attribute__((optimize("O3", "unroll-loops"))) void function { /* ... */ }
Một lưu ý cực kỳ quan trọng khi sử dụng pragma đó là chúng ta cần hiểu những chỉ thị được dùng sẽ hoạt động như thế nào và hoạt động một cách hiệu quả trong những hoàn cảnh nào. Bởi việc sử dụng từ khóa pragma một cách mù quáng sẽ làm cho chương trình không chỉ không thể được tối ưu mà còn bị tệ đi nhiều lần.
Một trong những ví dụ của việc sử dụng pragma một cách mù quáng đó là copy/paste 3 dòng code sau vào đầu của mọi chương trình, đây là một thói quen không được khuyến khích, mặc dù trong phạm vi lập trình thi đấu, chúng rất ít khi làm chương trình tệ đi:
#pragma GCC target("avx2")
#pragma GCC optimize("O3")
#pragma GCC optimize("unroll-loops")
Do đây là bài viết tập trung vào tối ưu tốc độ và bộ nhớ, chúng ta chỉ sẽ tìm hiểu về hai chỉ thị liên quan đến tối ưu là:
#pragma GCC optimize(...)
#pramge GCC target(...)
Chỉ thị #pragma GCC optimize
Đúng như cái tên, chỉ thị này sẽ ra lệnh cho trình biên dịch thay đổi một vài chi tiết trong quá trình biên dịch nhằm thực hiện các tối ưu phần cứng cho chương trình cuối cùng. Một số từ khóa thường dùng với chỉ thị GCC optimize là:
| Từ khóa | Công dụng | Lưu ý |
|---|---|---|
O2
|
Thực hiện tất cả các loại tối ưu "an toàn" -- tức sẽ không phản tác dụng trong mọi trường hợp. Ví dụ: sắp xếp các lệnh độc lập để hạn chế thời gian CPU không làm gì, loại bỏ các phép tính trung gian trùng lặp,... | Đã được tích hợp trong máy chấm Themis, VNOJ, Codeforces và đa số các Online Judges nên thường không cần dùng trong code. |
O3
|
Bao gồm các tối ưu thuộc nhóm O2 và các tối ưu khác như tự động vector hóa các phép tính độc lập với SIMD, sử dụng nhiều hàm nội tuyến hơn, gộp một nhóm các thao tác liên tiếp trong vòng lặp để giảm số lần kiểm tra điều kiện lặp (loop unroll),...
|
Trong khuôn khổ lập trình thi đấu, từ khóa O3 không mạo hiểm vì các code thường có độ dài không lớn hơn kích thước instruction cache.
|
Ofast
|
Bao gồm các tối ưu thuộc nhóm O3 và các tối ưu có phần mạo hiểm hơn, như bỏ qua tiêu chuẩn của ngôn ngữ lập trình về xử lý số thực, nguyên tắc quản lý con trỏ,... Việc sử dụng từ khóa Ofast làm chương trình mất đi sự chính xác khi thao tác với số thực, khó caching và debug hơn.
|
Từ khóa Ofast vẫn luôn là từ khóa gây tranh cãi vì bất lợi mà nó đem lại là không nhỏ. Đặc biệt khi làm việc với số thực, ta thường chấp nhận bỏ qua Ofast để chương trình được thực hiện một cách chặt chẽ hơn.
|
unroll-loops
|
Trình biên dịch sẽ gộp một nhóm các thao tác liên tiếp trong lặp để giảm số lần kiểm tra điều kiện lặp. |
Chỉ thị #pragma GCC target
Các chỉ thị GCC target giúp chúng ta thực hiện các chỉ thị liên quan để tập lệnh máy, ví dụ như sử dụng SIMD để thực hiện các lệnh liên tiếp không phụ thuộc vào nhau một cách song song. Một số từ khóa thường dùng với chỉ thị GCC target là:
| Từ khóa | Công dụng | Lưu ý |
|---|---|---|
avx, avx2 |
Chỉ định CPU sử dụng SIMD cho các lệnh có thể thực hiện song song (vectorization) nếu có. | Sử dụng cùng optimize("O3") hay optimize("unroll-loops") |
popcnt, lzcnt |
Làm cho tốc độ của __builtin_popcount() và __builtin_clz() nhanh hơn |
Lưu ý, độ phức tạp thời gian của hai hàm trên vẫn là ~\mathcal{O}(1)~ bất kể có sử dụng pragma hay không. |
abm, bmi, bmi2 |
Các tối ưu nhắm vào các thao tác trên bit nói chung. | |
fma |
Thực hiện các phép tính nhân rồi cộng ~d = a \cdot b + c~ trong một lần (fused multiply-add). | |
omit-frame-pointer |
Giúp tăng kích thước register có thể sử dụng để tính toán, tiện lợi hơn cho việc caching. | Đã được tích hợp vào chỉ thị optimize("O2"). |
Đây là một bài nộp trên nền tảng oj.uz đã có tận dụng tối đa các chỉ thị pragma để làm cho một thuật toán trâu có thể chạy vừa giới hạn thời gian. Tuy nhiên, đây là một bài tập có giới hạn khá lỏng để thí sinh sử dụng nhiều thuật toán khác nhau (chia căn, đường quét, chia để trị CDQ,...) và bản thân máy chấm của nền tảng này là tương đối mạnh.
Vì sao không nên sử dụng pragma trong thi cử?
Các chỉ thị pragma, ngoại trừ optimize("O2") đã được tích hợp trong máy chấm, nhìn chung là những tối ưu tạo ra nhiều biến số khi thực thi chương trình trên từng máy tính khác nhau; như đã đề cập, đôi khi việc sử dụng pragma một cách mù quáng không chỉ không thể tối ưu mà còn làm chậm tốc độ chương trình; chỉ thị Ofast thậm chí dẫn đến sai số tính toán và các hành vi không được kiểm soát (undefined behaviour).
Hơn nữa, trong môi trường lập trình thi đấu, việc xây dựng tư duy để thiết kế các thuật toán tối ưu được chú trọng hơn rất nhiều so với việc sử dụng những tối ưu không đáng kể để cố gắng ép các chương trình chưa tối ưu có thể vượt qua giới hạn thời gian.
Vì vậy, không chỉ tại kì thi Học sinh giỏi Quốc gia, nhiều kì thi lập trình thi đấu nói chung thường không cho phép sử dụng pragma để các thí sinh có thể tập trung vào các mặt tư duy, thiết kế thuật toán và cài đặt hơn là tối ưu phần cứng -- những bước tối ưu chỉ nên thực hiện sau khi đã có thuật toán tốt. Ngay ở những kì thi cho phép sử dụng pragma như ICPC hay IEEExtreme, các bài tập cũng được thiết kế sao cho thí sinh hoàn toàn có thể giải quyết mà không sử dụng từ khóa này.
Bài tập Codeforces 1146E -- Hot is Cold và lời giải vét cạn
Đây là một bài tập thú vị nhất thuộc vòng loại kì thi Forethought Future Cup, nếu xem các lời giải hiện đã nhận Accepted trên Codeforces, ta thấy các lời giải hầu hết rơi vào 1 trong 2 trường hợp sau:
- Có thời gian chạy dưới 200ms.
- Có thời gian chạy trên 950ms.
Nguyên nhân là do giới hạn của bài tập này là tương đối lỏng, hơn nữa, ta có thể tận dụng các nhận xét về tối ưu phần cứng để làm lời giải "vét cạn" trở nên nhanh hơn 1 giây. Trước tiên, ta cùng nghiên cứu đề bài.
Đề bài
Cho một dãy ~A~ gồm ~N~ phần tử và ~Q~ thao tác có dạng:
- Cho hai số nguyên ~s_j, x_j~ với ~s_j \in \{<, >\}~ và ~x_j~ là một số nguyên bất kỳ. Với mọi ~1 \leq i \leq N~, ta đổi dấu ~A_i~ nếu bất đẳng thức ~A_is_jx_j~ đúng.
Yêu cầu in ra mảng ~A~ sau khi thực hiện ~Q~ thao tác.
Giới hạn:
- ~1 \leq N \leq 10^5~
- ~-10^5 \leq A_i, x_j \leq 10^5~.
- Thời gian: ~1~ giây.
- Bộ nhớ: ~256~ MB.
Phân tích
Mình cực kì khuyến khích các bạn tự giải quyết bài toán bằng lời giải chuẩn trước khi đọc tiếp phần này.
Trong bài viết này, chúng ta sẽ không bàn luận về lời giải chuẩn của bài toán, mà sẽ phân tích các lời giải có thời gian chạy hơn 950ms -- một lời giải vét cạn vừa đủ giới hạn thời gian.
Có thể thấy, với các thao tác trong lời giải vét cạn (so sánh, gán, và truy cập mảng), thao tác truy cập mảng là nguyên nhân chính cho tốc độ chậm của thuật toán. Đây sẽ là cơ sở để ta thực hiện tối ưu phần cứng.
Trong lời giải ~\mathcal{O}(NQ)~, ta duyệt các thao tác từ ~1~ đến ~Q~ rồi duyệt mảng từ ~1~ đến ~N~ (hoặc ngược lại, duyệt mảng rồi duyệt thao tác). Khi này, thời gian truy cập mảng ~A~ là vô cùng lớn, vì phải cách ~N~ lần truy cập mảng thì ta mới truy cập lại một ô nhớ cũ. Điều này làm cache miss diễn ra rất nhiều nếu kích thước mảng lớn hơn sức chứa của các cache L1, L2, L3.
Thay vào đó, sử dụng một ý tưởng tương tự phương pháp phân khối trong nhân ma trận, ta chỉ giải bài toán cho một phần nhỏ của mảng ~A~ đủ để chứa trong L1 cache. Sau đó, lặp lại ý tưởng với phần còn lại của mảng. Nói cách khác, ta sẽ chia mảng ~A~ thành các nhóm gồm ~B~ phần tử rồi áp dụng lời giải vét cạn lên từng nhóm. Ta chọn ~B = 1024~ để mọi phần tử thuộc cùng một nhóm có thể nằm trọn trong L1 cache.
Dĩ nhiên, số thao tác truy cập phần tử vẫn là ~NQ~, tuy nhiên, khác biệt nằm ở thứ tự truy cập. Có thể thấy, ở cách ban đầu, thứ tự truy cập là như sau:
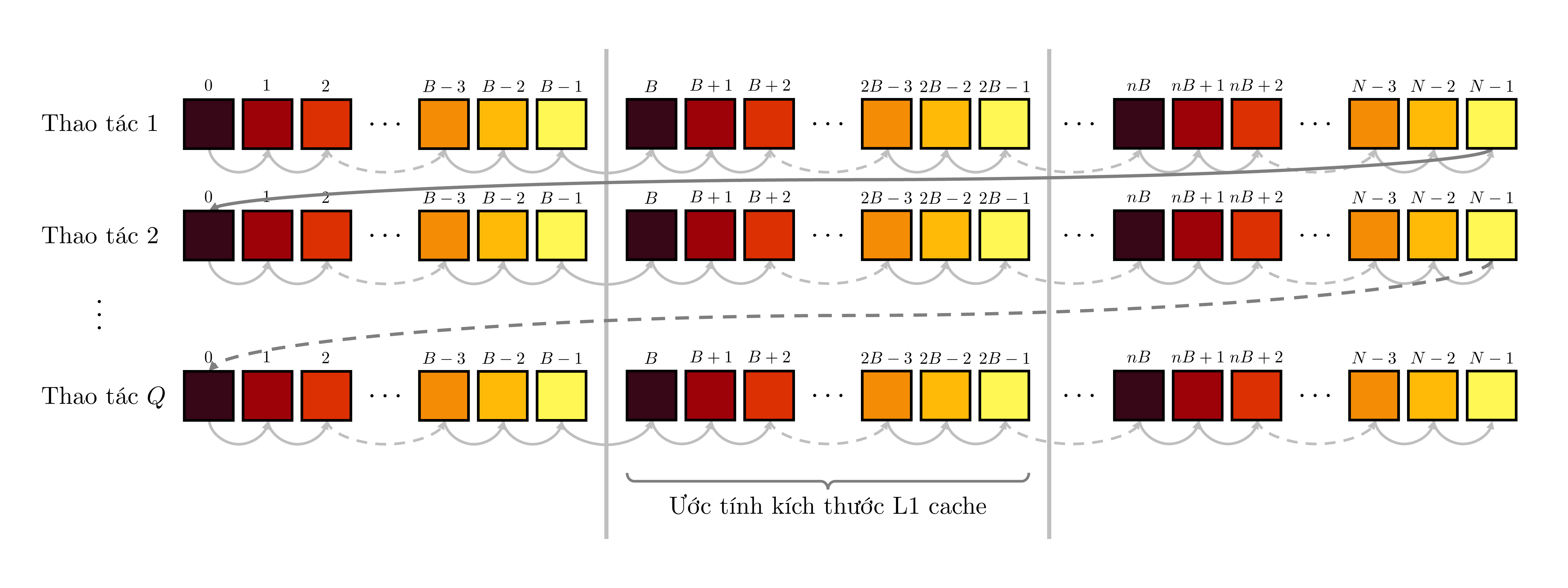
Tuy nhiên, ở cách chia nhóm, ta tận dụng rất triệt để việc các phần tử đã được đưa vào L1 cache sau thao tác đầu tiên:
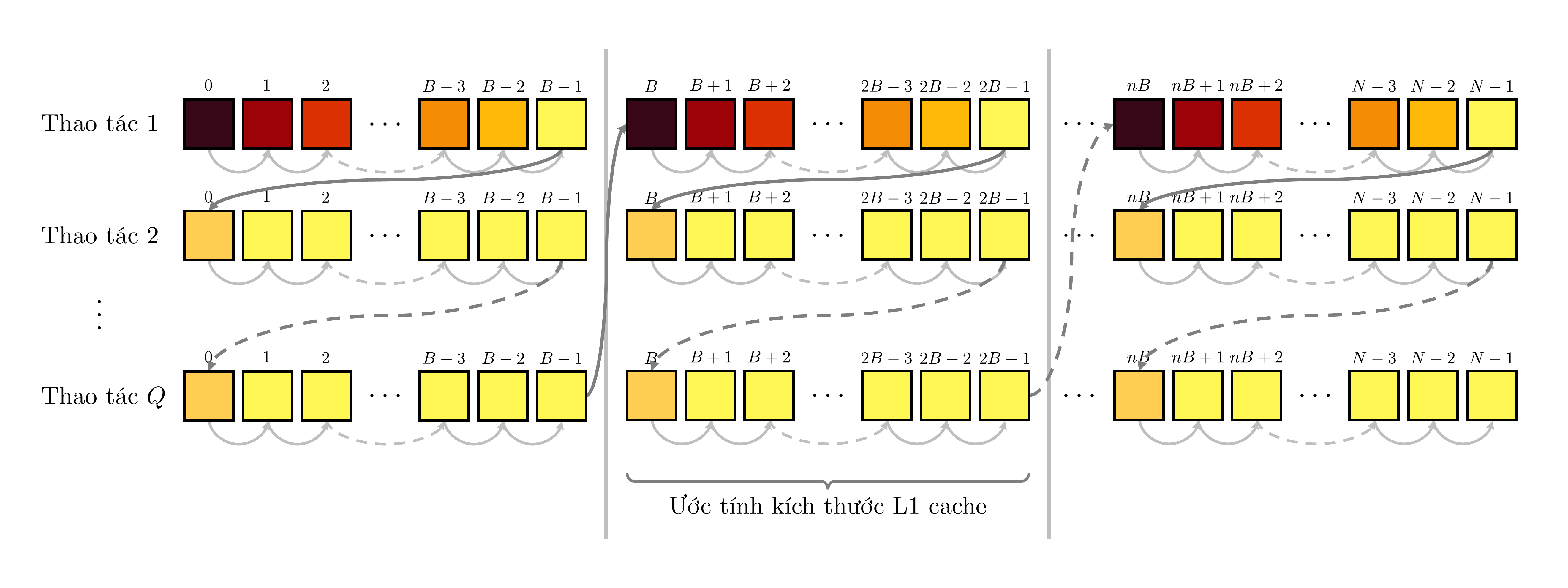
Lưu ý, màu sắc của mỗi phần tử dùng để ước lượng tốc độ truy cập chỉ mang tính tương đối, tốc độ truy cập các phần tử phụ thuộc vào rất nhiều yếu tố khác nhau đang diễn ra trong bộ nhớ máy tính.
Nếu kết hợp ý tưởng trên với chỉ định sử dụng SIMD (avx và avx2), chỉ định gộp phép nhân và phép cộng (fma), tối ưu Ofast, unroll-loops và input/output nhanh (sử dụng scanf), ta đã có thể giải quyết bài toán với lời giải "vét cạn".
Lời kết
Việc hiểu được cơ chế hoạt động của máy tính ở cấp độ bộ nhớ phần nào cũng sẽ giúp các lập trình viên có được cho mình những thói quen cài đặt hiệu quả hơn. Tuy nhiên, theo quan điểm cá nhân, mình nghĩ rằng nền tảng lớn nhất của một chương trình tốt vẫn luôn nằm ở ý tưởng thuật toán khôn ngoan, ở một độ phức tạp thời gian/bộ nhớ đủ tốt; chỉ khi đó, những tối ưu phần cứng như trên mới thực sự có ý nghĩa và tạo ra được một chương trình tối ưu.
Cảm ơn các bạn đã theo dõi bài viết. Xin chúc tất cả các bạn đọc của Tạp chí VNOI một mùa Tết thật ấm no, đầy đủ và hạnh phúc cùng gia đình, người thân và bạn bè!
Phụ lục
Code benchmark và vẽ biểu đồ
Bạn đọc có thể tham khảo các code đã được sử dụng để benchmark trong bài viết này:
- So sánh tốc độ truy cập của CPU theo từng cách duyệt
- So sánh tốc độ duyệt ~10^9~ thao tác với các CTDL khác nhau
- So sánh khả năng random-access trên các mảng có kích thước khác nhau
- So sánh tốc độ nhân ma trận
Các biểu đồ trong bài viết được thực hiện dựa trên thư viện Matplotlib.
Tài liệu tham khảo
- Igor Ostrovsky, Gallery of Processor Cache Effects.
- Jonathan Müller, Cache Friendly C++, Meeting C++ 2025.
- Prof. Peter YK Cheung, Introduction to Memories and Computer Architecture, Imperial College London.
- Nhiều tác giả, What does it mean for code to be "cache-friendly"?, Stack overflow.
- Tianqi Chen, Hardware Acceleration, Carnegie Mellon University.
- nor, GCC Optimization Pragmas.
- Options That Control Optimizations, GCC, the GNU Compiler Collection.
- Algorithmica, Contract Programming.
- Algorithmica, AoS and SoA.
- Alvin Wan, How to tile matrix multiplication.
Bình luận
Mình có đôi chút góp ý cho bài viết:
Throughput và latency của một lệnh không hẳn quyết định nhanh chậm mà vẫn còn dựa vào khả năng pipelining của CPU để "giấu" độ trễ cho một số nhóm lệnh. Khi đó nhiều lệnh có thể hoàn thành cùng lúc (và CPU có thể nhắm và chọn lệnh nào thực hiện trước để cho nhanh nhất mà không ảnh hướng tới thứ tự chương trình). Khi đó throughput thực sẽ phụ thuộc vào khả năng đáp ứng của các cổng ALU bên trong CPU
Một số lệnh Single-instruction Multiple-data (SIMD) mà tác giả so sánh không tương đương với nhau.
VPADDQ(vectorized-packed-add-quadword): cộng 4 số nguyên 64bit trên 2 thanh ghi AVX (256bit)VMULPD(vectorized-multiply-packed-double-precision): nhân 4 số thực double trên 2 thanh ghi AVXVDIVPD(vectorized-divide-packed-double-precision): chia 4 số thực double trên 2 thanh ghi AVXCác lệnh này cũng không gọi là "cơ bản" do sử dụng nguyên lý SIMD để xử lý nhiều dữ liệu nhanh hơn, sử dụng bởi complier tối ưu hoặc tự gọi intrinsic để sử dụng. Có thể tìm hiểu từng lệnh SIMD (x86) tại đây và đây
Tối ưu đệ quy còn có một kỹ thuật nữa là tail-call optimization: khi đệ quy, ta sẽ return chính hàm cần đệ quy. Khi bật tối ưu hàm gọi của chúng ta thành các bước nhảy, làm "phẳng hóa" thành những vòng lập tương đương với cách iterative
Trong các bài benchmark mình thắc mắc tác giả có cố định nhân CPU (set affinity) và cố định xung nhịp cho nhân (nhân chạy cố định một xung nhịp, không bị tăng giảm do các yếu tố boost hay quá nhiệt) hay không? Vì các CPU Alder Lake sử dụng kiến trúc hybrid có nhân lớn lẫn nhỏ. Sự khác biệt hiệu năng là lớn, và khi không thể xác định tiến trình đang chạy trên nhân nào sẽ ảnh hưởng đến độ chính xác của bài benchmark
-O3có thể tạo ra một số bug (hoặc thậm chí làm chương trình chậm đi) so với-O2vì compiler phải tối ưu mạnh hơn. Điểm chí mạng của-Ofastso với hai lựa chọn còn lại là việc bật cờ-ffast-mathđể tối ưu số thực. Khi đó compiler sẽ bỏ qua một số quy tắc khi làm việc với số thực (ví dụ kết quả phép tính(a + b) + cvàa + (b + c)là khác nhau!) hoặc các edge case của IEEE 754 (nguồn)Về phần lệnh máy thì em thấy các lệnh là dùng cho số dạng double (ngoại trừ vpaddq) chứ không phải long long. Nếu để các lệnh dùng cho long long thì sẽ tốt hơn.
Có thể thêm sự phân biệt giữa lệnh trên vector và lệnh trên giá trị thông thường.