Tunnel
Xem dạng PDF
Gửi bài giải
Điểm:
0,65 (OI)
Giới hạn thời gian:
1.0s
Giới hạn bộ nhớ:
256M
Input:
stdin
Output:
stdout
Dạng bài
Ngôn ngữ cho phép
C, C++, Go, Java, Kotlin, Pascal, PyPy, Python, Rust, Scratch
Dưới lòng đất của VNOI là hệ thống đường ngầm dày đặc gồm ~n~ địa điểm đánh số từ ~1~ đến ~n~. Có ~m~ đoạn đường ngầm, đoạn đường ngầm thứ ~i~ kết nối địa điểm ~u_i~ và ~v_i~ có chi phí là ~c_i~, nghĩa là muốn kích hoạt sử dụng đoạn đường hầm này phải trả chi phí là ~c_i~. Aaron và Hasun là đôi bạn thân đang hoạt động dưới lòng đất này.
Buổi sáng, Aaron cần đi từ ~A~ đến ~B~, và tất nhiên cậu chọn tuyến đường sao cho cần trả ít chi phí nhất.
Buổi chiều, Hasun cần đi từ ~C~ đến ~D~, nhưng may thay, những đoạn đường hầm mà buổi sáng Aaron đã trả chi phí để kích hoạt rồi thì Hasun có thể sử dụng mà không cần trả chi phí nữa.
Hãy hãy tính xem Hasun cần trả chi phí ít nhất là bao nhiêu?
Input:
- Dòng đầu tiên gồm hai số nguyên ~n, m~.
- Dòng thứ hai là bốn số nguyên ~A, B, C, D~.
- ~m~ dòng tiếp theo, mỗi dòng gồm ba số nguyên ~u_i, v_i, c_i~.
- Dữ liệu đảm bảo từ một địa điểm có thể đi đến mọi địa điểm khác, không có hai đoạn đường hầm nối cùng một cặp địa điểm.
Output:
- In ra một số nguyên là kết quả của bài toán.
Note
- Trong mọi test: ~A \neq B, C \neq D~, ~1 \le u_i < v_i \le n~, ~1 \le c_i \le 10^9~.
- Subtask 1 (~15\%~ số điểm): ~A=C~;
- Subtask 2 (~15\%~ số điểm): Có duy nhất một tuyến đường từ ~A~ đến ~B~ có giá trị nhỏ nhất;
- Subtask 3 (~30\%~ số điểm): ~n \le 300~;
- Subtask 4 (~40\%~ số điểm): ~2 \le n \le 10^5, 1 \le m \le 2 \times 10^5~
Ví dụ
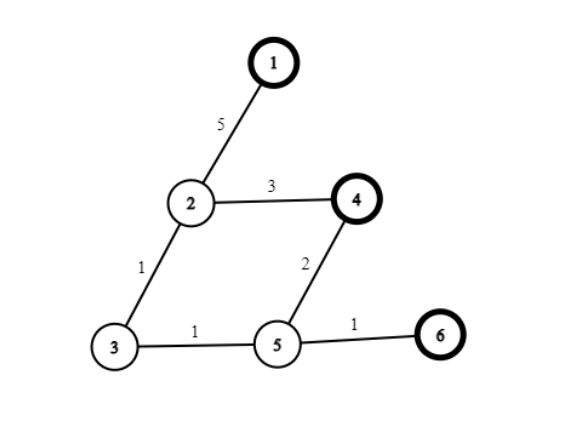
Input:
6 6
1 6 1 4
1 2 5
2 3 1
3 5 1
2 4 3
4 5 2
5 6 1
Output:
2
Giải thích:
- Chỉ có duy nhất một đường đi ngắn nhất từ ~1~ đến ~6~ là ~1-2-3-5-6~, nên Aaron sẽ sử dụng tuyến đường này.
- Hasun sẽ chỉ phải trả chi phí thêm đoạn đường hầm ~4-5~ với giá trị ~2~ đến di chuyển từ ~1~ đến ~4~.
Bình luận
Ai có solution bài này cho em tham khảo với
Comment này spoil thuật