Khi nghiên cứu về lý thuyết đồ thị, Nam đã tìm ra một đặc trưng cho đồ thị vô hướng. Cụ thể, với đồ thị vô hướng ~G~ gồm ~n~ đỉnh, xét lần lượt từng đỉnh từ ~1~ đến ~n~, với đỉnh ~i~, Nam tính được số ~a_i~ bằng số lượng đỉnh ~j~, thỏa mãn ~1 \le j < i~, mà ~j~ có cạnh nối với ~i~. Dãy số nguyên ~a_1, a_2, \ldots, a_n~ được gọi là dãy đặc trưng của đồ thị. Dễ nhận thấy rằng một đồ thị chỉ có duy nhất một dãy đặc trưng, tuy nhiên, có thể có nhiều đồ thị khác nhau nhưng có cùng một dãy đặc trưng.

Bẵng đi một thời gian, một hôm, Nam tìm lại được một file văn bản ghi một dãy số là một dãy đặc trưng của một đồ thị vô hướng. Tuy nhiên, dãy bị khuyết mất một số số và biết rằng bậc mỗi đỉnh của đồ thị này đều nhỏ hơn hoặc bằng ~b~. Nam muốn tính số lượng cách điền các số vào các vị trí bị khuyết để nhận được dãy ~f~ là dãy đặc trưng biết rằng:

1. Tồn tại ít nhất một đồ thị có dãy đặc trưng là ~f~;
2. Tất cả các đồ thị có dãy đặc trưng là ~f~ đều có bậc của mỗi đỉnh trong đồ thị nhỏ hơn hoặc bằng ~b~.

Yêu cầu: Cho số nguyên ~b~ và dãy đặc trưng bị khuyết, gọi ~S~ là số lượng cách điền các số vào các vị trí bị khuyết để nhận được dãy ~f~ là dãy đặc trưng thỏa mãn, hãy tính ~S \bmod (10^9 + 7)~, trong đó ~\bmod~ là phép toán chia lấy dư. Hai cách điền gọi là khác nhau nếu như tồn tại một vị trí khuyết mà giá trị điền vào trong cách này khác với giá trị điền vào trong cách kia.

Dữ liệu

Vào từ file văn bản GRAPH.INP:

• Dòng đầu tiên chứa hai số nguyên dương ~n, b~ (~b \le n~);
• Dòng thứ hai chứa ~n~ số nguyên, số thứ ~i~ có giá trị ~a_i~ (~1 \le i \le n~; ~0 \le a_i \le i - 1~ hoặc ~a_i = -1~) mô tả dãy đặc trưng. Giá trị ~a_i = -1~ có nghĩa là vị trí thứ ~i~ bị khuyết.

Các số trên cùng một dòng cách nhau bởi dấu cách.

Kết quả

Ghi ra file văn bản GRAPH.OUT một số nguyên duy nhất là giá trị ~S \bmod (10^9 + 7)~.

• Có ~25\%~ số test ứng với ~25\%~ số điểm của bài thỏa mãn: ~n \le 6~;
• ~30\%~ số test khác ứng với ~30\%~ số điểm của bài thỏa mãn: ~n \le 200~ và chỉ có duy nhất một ô bị khuyết;
• ~25\%~ số test khác ứng với ~25\%~ số điểm của bài thỏa mãn: ~n \le 200~;
• ~20\%~ số test còn lại ứng với ~20\%~ số điểm của bài thỏa mãn: ~n \le 2000~.

Ví dụ

Input

4 1
-1 -1 1 -1

Output

1

Giải thích

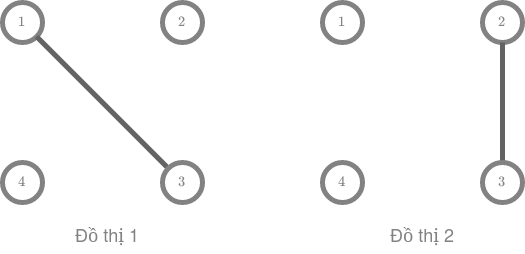
Có duy nhất một dãy đặc trưng thỏa mãn là ~(0, 0, 1, 0)~ và có tất cả ~2~ đồ thị cùng có dãy đặc trưng này như trong hình sau: