English below the Vietnamese tutorial

Subtask 1

Nhiệm vụ tương đương với việc tìm đường đi ngắn nhất biến một trạng thái bảng thành trạng thái khác.

Lưu ý rằng với mỗi ô chưa được phủ ~(r, c)~, một khi bạn bắt đầu đặt các tromino hình chữ L, cách lát sẽ là duy nhất. Vì vậy một ô ~(r, c)~ có thể đại diện cho cả trạng thái bảng. Tổng cộng có ~2^k × 2^k~ trạng thái.

Với giới hạn của subtask này, ta có thể liệt kê mọi trạng thái và chạy BFS.

• Xây dựng đồ thị trong đó mỗi đỉnh tương ứng một trạng thái bảng (tức một ô), và hai đỉnh kề nhau nếu chuyển được từ trạng thái này sang trạng thái kia chỉ bằng một lần xoay tromino.

Trong bước tiền xử lý cần sinh đồ thị. Để tạo cạnh, có thể mô phỏng mọi phép xoay hợp lệ:

• Mô phỏng sao chép. Sau mỗi lần xoay, sao chép toàn bộ bảng rồi tiếp tục từ bản sao.
• DFS tại chỗ. Giữ duy nhất một bảng: xoay, đệ quy sang trạng thái lân cận, và khi back-track thì hoàn tác lại phép xoay.

Độ phức tạp

• Tiền xử lý: ~O((2^k × 2^k)^2)~ nếu sao chép bảng mỗi bước, hoặc ~O(2^k × 2^k)~ nếu chỉ giữ một bảng và back-track.
• ~O(2^k × 2^k)~ cho mỗi truy vấn.

Subtask 2

Độ dài đường đi ngắn nhất giữa hai đỉnh chỉ ~O(2^k)~, nên ta có thể trả lời mỗi truy vấn trong đúng thời gian đó bằng cách đi theo chính đường đi ấy.

Những nhận xét quan trọng về bảng:

1. Bảng ~2^1 × 2^1~ chứa đúng một tromino chữ L, tạo thành hình vuông; hai ô cùng nằm trên một cạnh là kề nhau.
2. Bảng ~2^2 × 2^2~ tách được thành bốn bảng con ~2^1 × 2^1~, và tromino ở giữa nối bốn góc trong của các bảng con.
3. …
4. Tổng quát, bảng ~2^k × 2^k~ tách thành bốn bảng con ~2^{k-1} × 2^{k-1}~, kèm một tromino trung tâm nối bốn góc trong của chúng.

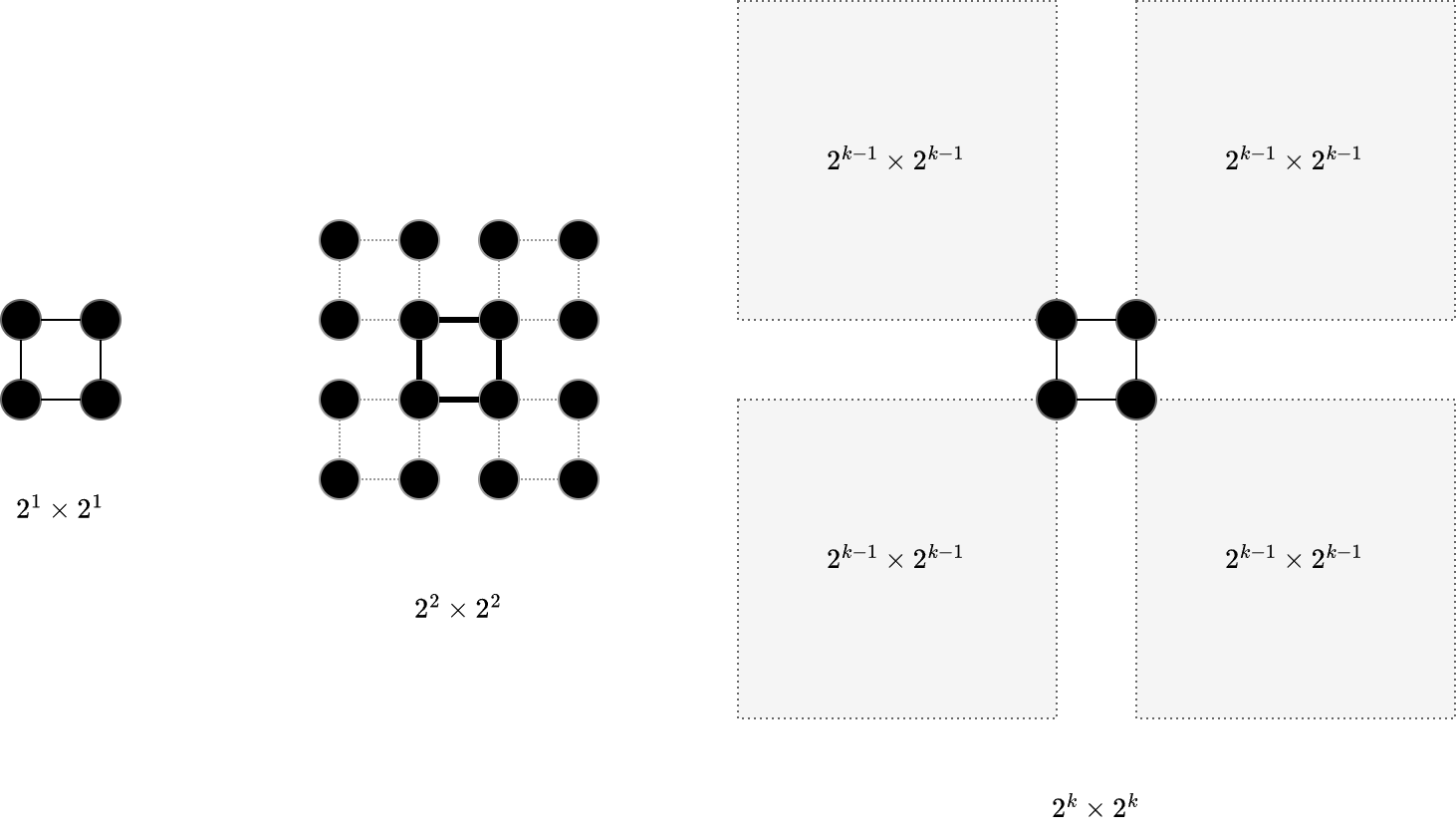
Nhờ cấu trúc đó, đường đi từ ~u~ tới ~v~ có thể tách thành các đoạn nhỏ hơn nằm trọn trong cùng một góc phần tư.

Gọi hàm ~\mathrm{md}(u, v)~ là khoảng cách Manhattan giữa ~u~ và ~v~. Định nghĩa thủ tục ~\mathrm{shortest\_path}(board, u, v)~ như sau:

• Trường hợp cơ bản

  • Nếu ~u = v~, đáp án là ~0~.
  • Nếu bảng kích thước ~2^1 × 2^1~, đáp án là ~\mathrm{md}(u, v)~ (đi quanh cạnh hình vuông).

• Đệ quy - bảng kích thước ~2^k × 2^k~ với ~k ≥ 2~.

  • Chia thành bốn bảng con ~2^{k-1} × 2^{k-1}~.
    • ~board_u~: bảng con chứa ~u~.
    • ~board_v~: bảng con chứa ~v~.
    • ~joint_u~: góc trong của ~board_u~.
    • ~joint_v~: góc trong của ~board_v~.
  • Nếu ~board_u = board_v~, chỉ cần đệ quy trong bảng con đó: ~\mathrm{shortest\_path}(board_u, u, v)~.

  • Ngược lại, chia đường đi thành ba đoạn:

    1. ~u → joint_u~ (trong ~board_u~)
    2. ~joint_u → joint_v~ (qua tromino trung tâm)
    3. ~joint_v → v~ (trong ~board_v~)

    Đáp án:

  $$\mathrm{shortest\_path}(board_u, u, joint_u) + \mathrm{md}(joint_u, joint_v) + \mathrm{shortest\_path}(board_v, joint_v, v)$$

Không cần tiền xử lý; mỗi truy vấn chạy trong ~O(2^k)~.

Subtask 3

Với ~k~ lên tới ~60~, ~O(2^k)~ quá chậm; ta tối ưu xuống ~O(k)~ cho mỗi truy vấn.

• Sau lần tách đầu tiên ~u → joint_u → joint_v → v~, cả ~joint_u~ và ~joint_v~ đều là góc của một bảng con.
• Nếu ta tiếp tục tách đoạn ~u → joint_u~ thành ~u → joint_u' → joint_u'' → joint_u~, thì ~joint_u''~ cũng là một góc.
• Quan sát: ~joint_u''~ và ~joint_u~ là hai góc đối diện của cùng một bảng con.

Với hai góc đối diện ~p~, ~q~ của bảng ~2^t × 2^t~, đường đi ngắn nhất chính là ~\mathrm{md}(p, q)~. Như vậy ta không cần tách đường đi thành cách đoạn con nhỏ hơn.

Bổ sung trường hợp cơ bản cho thuật toán ở subtask 2:

• Nếu ~u~ và ~v~ là hai góc đối diện của bảng hiện tại, trả về ~\mathrm{md}(u, v)~.

Một cách kiểm tra 2 góc đối diện đơn giản: trong bảng ~2^k × 2^k~, hai góc đối diện thỏa ~\mathrm{md}(u, v) = 2 × (2^k - 1)~, cũng là khoảng cách lớn nhất trong bảng.

Phân tích độ phức tạp thời gian:

• Tách ban đầu chỉ thực hiện một lần.
• Đoạn ~u → joint_u~ bị tách tối đa ~k~ lần (mỗi cấp một lần).
• Tương tự, đoạn ~joint_v → v~ cũng tối đa ~k~ lần.

Vì vậy mỗi truy vấn chạy trong ~O(k)~.

Subtask 1

The task is equivalent to finding the shortest path that transforms one board state into another.

Notice that for every uncovered cell ~(r, c)~, once you start placing the L-shaped trominoes, the tiling is unique. Therefore a single cell ~(r, c)~ can represent an entire board state. In total there are ~2^k \times 2^k~ states.

Given the limits of this subtask, we can simply enumerate all states and run a BFS.

• Build a graph where each vertex corresponds to a board state (i.e. a cell), and two vertices share an edge if one state can be reached from the other by a single tromino rotation.

During preprocessing you have to generate this graph. To create the edges you can simulate every legal rotation:

• Copy-based simulation. After each rotation, copy the whole board and continue from the new copy.
• In-place DFS. Keep just one board: perform the rotation, recurse to the neighbour state, and when backtracking undo the rotation.

Time complexity

• Preprocessing: ~O\bigl((2^k \times 2^k)^2\bigr)~ if you copy the board every step, or ~O(2^k \times 2^k)~ if you keep a single board and back-track.
• ~O(2^k \times 2^k)~ per query.

Subtask 2

The shortest path between any two vertices has length ~O(2^k)~, which suggests we can answer each query in that time by following exactly that path.

Key observations about the board:

1. A ~2^1 \times 2^1~ board contains exactly one L-tromino. It forms a square; two cells on the same edge are adjacent.
2. A ~2^2 \times 2^2~ board splits into four ~2^1 \times 2^1~ sub-boards, and the central tromino connects the four inner corners of those sub-boards.
3. …
4. In general, a ~2^k \times 2^k~ board splits into four ~2^{k-1} \times 2^{k-1}~ quadrants, plus a central tromino that joins the four inner corners of the quadrants.

With this structure, a path from ~u~ to ~v~ can be decomposed into shorter paths that stay inside the same quadrant.

Let ~\mathrm{md}(u, v)~ be the Manhattan distance between ~u~ and ~v~. Define ~\mathrm{shortest\_path}(board, u, v)~ as follows:

• Base cases

  • If ~u = v~, answer is ~0~.
  • If the board is ~2^1 \times 2^1~, answer is ~\mathrm{md}(u, v)~ (walk along the square's edges).

• Recursive case - board size ~2^k \times 2^k~ with ~k ≥ 2~.

  • Split it into four ~2^{k-1} \times 2^{k-1}~ quadrants.
    • ~board_u~: quadrant containing ~u~.
    • ~board_v~: quadrant containing ~v~.
    • ~joint_u~: inner corner of ~board_u~.
    • ~joint_v~: inner corner of ~board_v~.
  • If ~board_u = board_v~, recurse inside that quadrant: ~\mathrm{shortest\_path}(board_u, u, v)~.

  • Otherwise split the full path into three segments:

    1. ~u → joint_u~ (inside ~board_u~)
    2. ~joint_u → joint_v~ (via the central tromino)
    3. ~joint_v → v~ (inside ~board_v~)

    Answer:

  $$\mathrm{shortest\_path}(board_u, u, joint_u) + \mathrm{md}(joint_u, joint_v) + \mathrm{shortest\_path}(board_v, joint_v, v)$$

No preprocessing is required and each query runs in ~O(2^k)~.

Subtask 3

With ~k~ up to ~60~, ~O(2^k)~ is far too slow. We can optimise the previous method to ~O(k)~ per query.

• After the first split ~u → joint_u → joint_v → v~, both ~joint_u~ and ~joint_v~ are corners of a sub-board.
• If we later split ~u → joint_u~ into ~u → joint_u' → joint_u'' → joint_u~, then ~joint_u''~ is also a corner.
• Observation: ~joint_u''~ and ~joint_u~ are opposite corners of the same sub-board.

For two opposite corners ~p~, ~q~ of a ~2^t \times 2^t~ board, the shortest path length equals ~\mathrm{md}(p, q)~. Hence we never need to split such a segment again.

Add this extra base case to the algorithm in the subtask 2:

• If ~u~ and ~v~ are opposite corners of the current board, return ~\mathrm{md}(u, v)~.

A simple test: in a ~2^k \times 2^k~ board, opposite corners satisfy ~\mathrm{md}(u, v) = 2 \times (2^k - 1)~, which is also the maximum possible distance inside the board.

Complexity:

• The initial split is done once.
• The path ~u → joint_u~ is split at most ~k~ times (one per level).
• Symmetrically, ~joint_v → v~ is also split at most ~k~ times.

Thus each query runs in ~O(k)~.

use std::{io::*, ops::*};

#[derive(Debug, Clone, Copy, Eq, PartialEq, Ord, PartialOrd)]
struct Cell(usize, usize);

impl Cell {
    fn inside(&self, top_left: Cell, bottom_right: Cell) -> bool {
        self.0 >= top_left.0 && self.0 <= bottom_right.0 && self.1 >= top_left.1 && self.1 <= bottom_right.1
    }

    fn mul(self, scalar: usize) -> Self {
        Self(self.0 * scalar, self.1 * scalar)
    }

    fn mahattan_dist(self, other: Cell) -> usize {
        self.0.abs_diff(other.0) + self.1.abs_diff(other.1)
    }
}

impl Add<Cell> for Cell {
    type Output = Cell;
    fn add(self, other: Cell) -> Self::Output {
        Self(self.0 + other.0, self.1 + other.1)
    }
}

impl Sub<Cell> for Cell {
    type Output = Cell;
    fn sub(self, other: Cell) -> Self::Output {
        Self(self.0 - other.0, self.1 - other.1)
    }
}

#[derive(Debug, Clone, Copy, Eq, PartialEq)]
struct PartBoard {
    k: usize,
    top_left: Cell,
}

impl PartBoard {
    fn size(&self) -> usize {
        1 << self.k
    }

    fn half(&self) -> usize {
        1 << (self.k - 1)
    }

    fn bottom_right(&self) -> Cell {
        self.top_left + Cell(1 << self.k, 1 << self.k) - Cell(1, 1)
    }

    fn get_quad(&self, cell: Cell) -> Cell {
        assert!(cell.inside(self.top_left, self.bottom_right()));
        let half = self.half();
        let is_bottom = cell.0 - self.top_left.0 >= half;
        let is_right = cell.1 - self.top_left.1 >= half;
        Cell(is_bottom as usize, is_right as usize)
    }

    fn part_of(&self, quad: Cell) -> Self {
        Self { k: self.k - 1, top_left: self.top_left_of(quad) }
    }

    fn joint_of(&self, quad: Cell) -> Cell {
        self.top_left + Cell(self.half() - 1, self.half() - 1) + quad
    }

    fn top_left_of(&self, quad: Cell) -> Cell {
        self.top_left + quad.mul(self.half())
    }
}

fn dist(pb: PartBoard, u: Cell, v: Cell) -> usize {
    if pb.k == 0 {
        return 0;
    }
    let diag_dist = (pb.size() - 1) * 2;
    if u.mahattan_dist(v) == diag_dist {
        return diag_dist;
    }

    let quad_u = pb.get_quad(u);
    let quad_v = pb.get_quad(v);
    if quad_u == quad_v {
        dist(pb.part_of(quad_u), u, v)
    } else {
        let u_joint = pb.joint_of(quad_u);
        let v_joint = pb.joint_of(quad_v);

        u_joint.mahattan_dist(v_joint) + dist(pb.part_of(quad_u), u, u_joint) + dist(pb.part_of(quad_v), v, v_joint)
    }
}

fn main() {
    let stdout = std::io::stdout();
    let mut writer = std::io::BufWriter::new(stdout.lock());
    let lines = std::io::stdin().lines().map(|x| x.unwrap());
    let mut tokens = lines.flat_map(|x| x.split_ascii_whitespace().map(|x| x.to_string()).collect::<Vec<_>>());
    let mut next_usize = move || tokens.next().unwrap().parse::<usize>().ok().expect("Failed to parse");

    let k = next_usize();
    let q = next_usize();

    let mut cur_empty = Cell(0, 0);

    for _qid in 0..q {
        let r = next_usize();
        let c = next_usize();
        let target = Cell(r, c);

        let ans = dist(PartBoard { k, top_left: Cell(0, 0) }, cur_empty, target);

        writeln!(writer, "{ans}").ok();
        cur_empty = target;
    }
}