Bài học đệ quy đầu tiên
Xem dạng PDFChắc hẳn bạn nào học tin cũng biết đến câu đố dưới đây khi được học đến phần đệ quy.
Cho một bảng có kích thước ~2^k \times 2^k~ và các mảnh ghép hình chữ L được tạo thành bởi 3 ô vuông. Các mảnh ghép có thể được xoay tùy ý. Tìm cách đặt các mảnh ghép lên bảng sao cho ngoại trừ ô ~(r, c)~, các ô trên bảng đều bị bao phủ bởi chính xác một mảnh ghép.
Bí quyết để giải được câu đố này là cần nhận thấy ta có thể xếp được các mảnh ghép chữ L lớn hơn từ các mảnh ghép nhỏ, và sử dụng các mảnh ghép lớn để lát vào bảng. Để giúp các bạn gợi nhớ, tóm tắt thuật toán tổng quát để giải câu đố này sẽ được mô tả lại ở phần chú thích phía dưới.
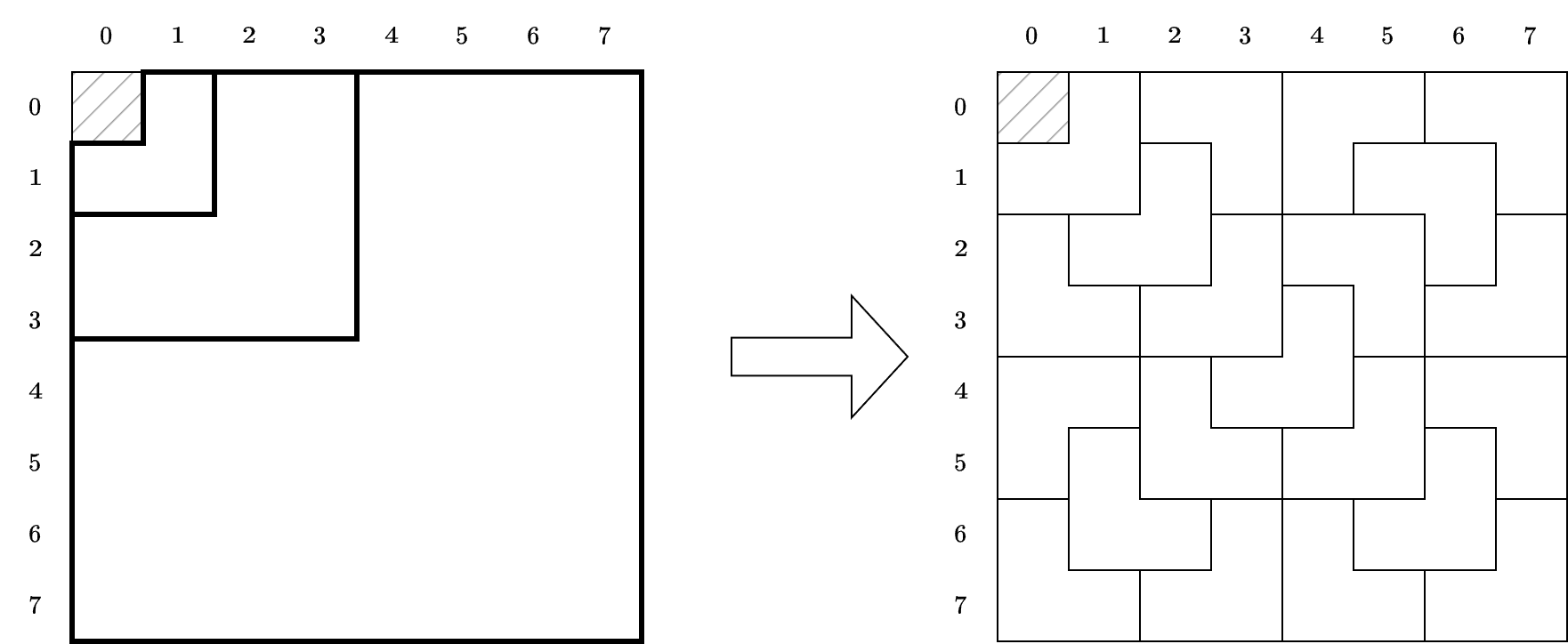
Sau khi giảng cho bạn thuật toán này, thầy giáo đã rất kinh ngạc khi thấy bạn đã hiểu và có khả năng áp dụng nó rất nhanh. Thầy giáo đành phải ra thêm bài tập bổ sung xoay quanh thuật toán này. Cho một bảng có kích thước ~2^k \times 2^k~. Các hàng được đánh số ~0, 1, 2, \ldots, 2^k - 1~ từ trên xuống dưới, và các cột được đánh số ~0, 1, 2, \ldots, 2^k - 1~ từ trái qua phải. Ban đầu bảng đã được lát bằng các mảnh ghép chữ L sao cho ô ~(0, 0)~ là ô không bị bao phủ theo như thuật toán bạn đã được học.
Sau đó thầy giáo có ~q~ câu đố nhỏ liên tiếp. Với câu đố thứ ~i~, thầy giáo muốn biến bảng, từ trạng thái ngay trước câu đố này, đến trạng thái mà bảng có ô ~(r_i, c_i)~ không được bao phủ. Để làm điều này thầy giáo cho bạn thực hiện thao tác sau (không hoặc nhiều lần):
- Chọn một mảnh ghép chữ L mà đang kề với 2 cạnh của ô không được bao phủ. Xoay mảnh ghép này đi 90 độ theo chiều mà bạn muốn. Có thể thấy sau thao tác này, một ô mới sẽ trở thành ô không được bao phủ.
Có thể chỉ ra rằng, với cách lát ban đầu theo như thuật toán mà bạn đã được học, lúc nào cũng tồn tại dãy thao tác xoay các mảnh ghép, để biến bảng có ô chưa bao phủ từ một ô này đến một ô khác.
Dưới đây là minh họa cách thực hiện thao tác cho bảng ~2^2 \times 2^2~. Thầy giáo đã ra ba câu đố, với mỗi câu cần biến đổi ô không bao phủ như sau:
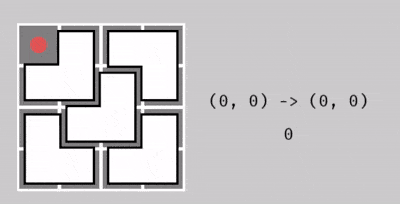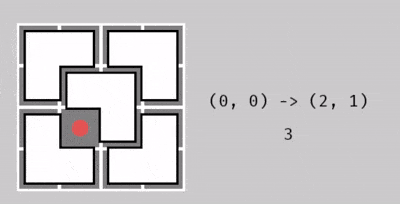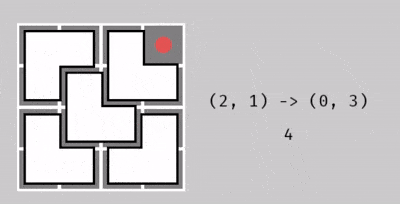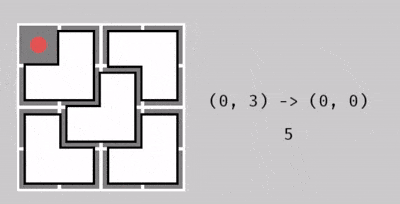
Từ ô ~(0, 0)~ thành ô ~(2, 1)~, với 3 thao tác.
Từ ô ~(2, 1)~ thành ô ~(0, 3)~, với 4 thao tác.
Từ ô ~(0, 3)~ thành ô ~(0, 0)~, với 5 thao tác.
Thầy giáo muốn bạn giải đáp các câu đố càng nhanh càng tốt. Do đó với mỗi câu đố, bạn muốn tìm xem cần thực hiện ít nhất bao nhiêu thao tác để đáp câu đố đó.
Input
Dòng đầu tiên gồm hai số nguyên ~k~ và ~q~ (~1 \le k \le 60~, ~1 \le q \le 10^5~). Tham số ~k~ cho biết kích thước của bảng là ~2^k \times 2^k~, và thầy giáo sẽ hỏi bạn ~q~ câu đố.
Dòng thứ ~i~ trong ~q~ dòng tiếp theo chứa hai số nguyên ~r_i~ và ~c_i~ (~0 \le r_i, c_i < 2^k~) – ô không được bao phủ sau câu đố thứ ~i~.
Output
In ra ~q~ dòng. Dòng thứ ~i~ chứa một số nguyên là số thao tác ít nhất để giải đáp câu đố thứ ~i~.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~500~ | ~k \le 5~, ~q \le 1000~ |
| 2 | ~750~ | ~k \le 10~ |
| 3 | ~1000~ | Không có ràng buộc gì thêm |
| Tổng | ~2250~ |
Sample Input 1
2 3
2 1
0 3
0 0
Sample Output 1
3
4
5
Sample Input 2
3 4
6 2
7 7
3 4
4 6
Sample Output 2
10
10
7
5
Notes
Ví dụ đầu tiên đã được minh họa qua hình ở phía trên.
Dưới đây là minh họa cho ví dụ thứ hai.
Tóm tắt thuật toán lát các mảnh ghép chữ L
Từ các mảnh ghép chữ L nhỏ, ta có thể tạo ra các mảnh ghép cũng có hình chữ L to hơn theo cách ghép sau:
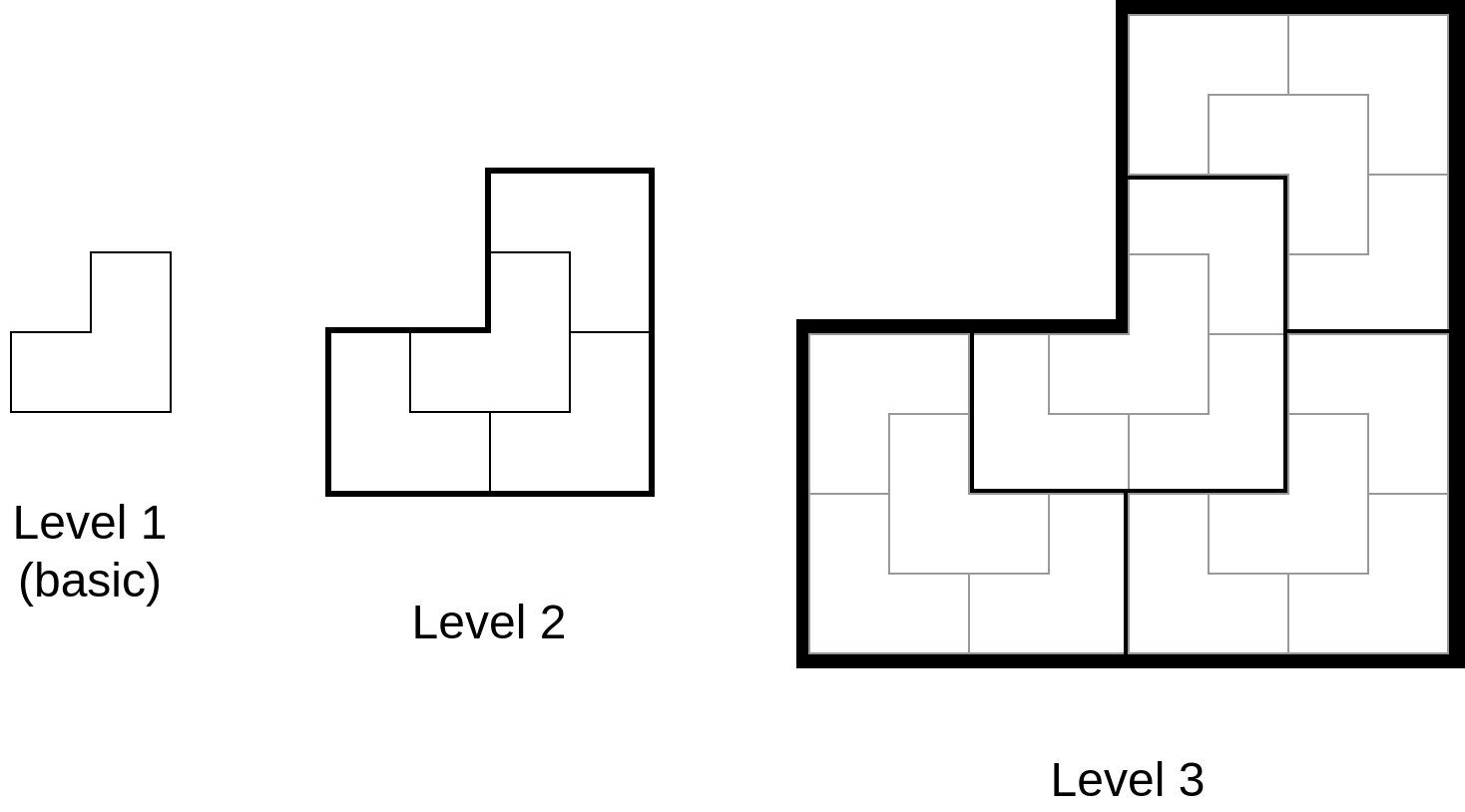
Để lát các mảnh ghép chữ L vào bảng, sao cho ô ~(0, 0)~ không bị bao phủ, ta có thể ghép chúng thành các mảnh ghép chữ L to hơn và chồng chúng lên như sau:
Bình luận
ae nao k bt lam bai thi cu bao toi