Subtask 1: ~n, m \leq 100~

Duyệt hai cạnh ~i, j~ sau đó sử dụng Dijkstra trong ~O(m \log n)~ để tìm đường đi ngắn nhất.

Độ phức tạp: ~O(m^3 \log n)~.

Subtask 2: ~n, m \leq 2000~

Ta có thể bỏ duyệt ~j~ mà chỉ lấy ~w_j~ lớn nhất mà ~i < j~. Sau đó làm như subtask 1.

Độ phức tạp: ~O(m^2 \log n)~

Subtask 3: ~m = n - 1~.

Vì đồ thị lúc này là cây nên sẽ chỉ có duy nhất một đường đi từ đỉnh ~1~ tới đỉnh ~n~ cho nên nếu ta tăng bất kì cạnh nào trên đường đi này cũng làm tăng độ dài đường đi ngắn nhất. Khi đó ta có thể duyệt từng cạnh trên đường đi này và thử tìm ~w_i~ lớn nhất mà có thể cộng vào cạnh đó.

Độ phức tạp: ~O(m)~.

Subtask 4: ~w_i = 1~.

Nhận xét 1: Đáp án có thể tăng lên nếu ta tăng một cạnh nằm trên ít nhất một đường đi ngắn nhất từ ~1~ đến ~n~.

Gọi ~dist(u, v)~ là khoảng cách ngắn nhất từ đỉnh ~u~ đến đỉnh ~v~. Với mỗi cạnh ~(u, v)~, cạnh này sẽ nằm trên ít nhất một đường đi ngắn nhất khi ~dist(1, u) + 1 + dist(v, n) = dist(1, n)~ (hoặc ~dist(1, v) + 1 + dist(u, n) = dist(1, n)~).

Nhận xét 2: Đáp án chỉ tăng lên nếu ta tăng một cạnh nằm trên tất cả các đường đi từ ~1~ đến ~n~.

Vậy ta chỉ cần tìm xem có tồn tại một cạnh mà nằm trên tất cả các đường đi ngắn nhất từ ~1~ đến ~n~. Điều kiện để cạnh thứ ~i~ nằm trên mọi đường đi từ ~1~ đến ~n~ trong trường hợp này là:

• Cạnh này nằm trên ít nhất một đường đi ngắn nhất từ ~1~ đến ~n~.

• Không tồn tại cạnh ~j~ khác mà ~dist(1, u_j) = dist(1, u_i)~ và ~dist(v_j, n) = dist(v_i, n)~.

Điều kiện này là bởi cạnh thứ ~i~ phải là cạnh thứ ~dist(1, u_i) + 1~ trên đường đi từ ~1~ đến ~n~, và nếu tồn tại cạnh ~j~ thỏa mãn điều kiện thứ hai thì vai trò của hai cạnh là như nhau và ta không thể tăng cùng lúc cả hai cạnh.

Chú ý là ta không thể tăng cạnh thứ ~m~.

Độ phức tạp: ~O(m)~ nếu dùng BFS thay cho Dijkstra.

Subtask 5: ~w_i \leq 10~.

Vì ~w_i \leq 10~ nên đáp án chỉ có thể thuộc đoạn ~[dist(1, n), dist(1, n) + 10]~. Với mỗi ~X \in [dist(1, n), dist(1, n) + 10]~, ta sẽ tìm xem có cách tăng sao cho đáp án lớn hơn hoặc bằng ~X~ hay không.

Gọi ~P_i~ là lượng lớn nhất mà ta có thể tăng cạnh ~i~ lên (chính là ~w_j~ lớn nhất trong Subtask 2). Để làm cho ~dist(1, n) \geq X~, ta phải tìm một cạnh ~i~ thỏa mãn:

• Cạnh đó nằm trên mọi đường đi từ ~1~ đến ~n~ mà có độ dài ngắn hơn ~X~.

• ~dist(1, u_i) + w_i + P_i + dist(v_i, n) \geq X~ và ~dist(1, v_i) + w_i + P_i + dist(u_i, n) \geq X~.

Vì điều kiện thứ hai có thể kiểm tra khá dễ dàng, nên việc của ta chỉ là tìm các cạnh thỏa mãn điều kiện thứ nhất. Gọi các cạnh thỏa mãn điều kiện thứ nhất là cạnh tốt. Để tìm các cạnh tốt, đầu tiên ta dựng một đồ thị mới ~H~, trong đó các cạnh trong ~H~ chính là các cạnh trong đồ thị ban đầu mà thuộc vào ít nhất một đường đi từ ~1~ đến ~n~ mà có độ dài ngắn hơn ~X~ (việc kiểm tra các cạnh cũng giống Subtask 4).

Nhận xét: Cạnh tốt khi xóa đi sẽ khiến ~1~ và ~n~ không còn liên thông trong ~H~.

Chứng minh: Hiển nhiên nếu xóa đi một cạnh mà ~1~ và ~n~ không còn liên thông thì cạnh đó chắc chắn là cạnh tốt, nên giờ ta sẽ chứng minh chiều ngược lại. Giả sử ta xóa cạnh tốt ~i~, mà ~1~ với ~n~ vẫn còn liên thông. Khi đó tồn tại đường đi ~1 = a_1 \xrightarrow{\ \ e_1 \ \ } a_2 \ldots a_{k - 1} \xrightarrow{e_{k - 1}} a_k = n~. (đường đi này không nhất thiết phải ngắn hơn ~X~). Vì ~i~ là cạnh tốt nên tồn tại một đường đi ngắn hơn ~X~ mà đi qua cạnh ~e_1~ và ~i~, và cũng tồn tại một đường đi ngắn hơn ~X~ mà đi qua cạnh ~i~ và ~e_k~. Khi đó phải tồn tại cạnh ~e_{j - 1}~ và ~e_j~ sao cho ~e_{j - 1}~ đứng trước cạnh ~i~ nhưng ~e_{j}~ đứng sau cạnh ~i~.

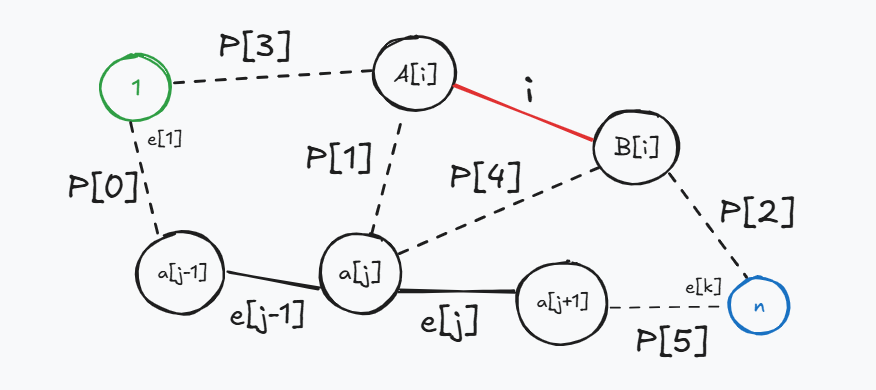
Trong hình trên (các đường nét đứt thể hiện đường đi, các đường liền thể hiện cạnh):

• Đường đi từ ~1~ đến ~n~: ~1 \xrightarrow{\ P_0\ } a_{j - 1} \xrightarrow{e_{j - 1}} a_j \xrightarrow{\ \ e_j\ \ } a_{j + 1} \xrightarrow{\ P_5\ } n~.

• Đường đi ngắn hơn ~X~ mà đi qua cạnh ~e_1~ và ~i~: ~1 \xrightarrow{\ P_0\ } a_{j - 1} \xrightarrow{e_{j - 1}} a_j \xrightarrow{\ P_1\ } A_{i} \xrightarrow{\ \ i\ \ } B_i \xrightarrow{\ P_2 \ } n~.

• Đường đi ngắn hơn ~X~ mà đi qua cạnh ~i~ và ~e_k~: ~1 \xrightarrow{\ P_3\ } A_i \xrightarrow{\ \ i\ \ } B_i \xrightarrow{\ P_4\ } a_j \xrightarrow{\ \ e_j\ \ } a_{j + 1} \xrightarrow{\ P_5\ } n~.

Đặt ~T_1 = P_3 + P_1 + P_4 + P_2~, ~T_2 = P_0 + e_{j - 1} + e_j + P_5~. Do ~T_1 + T_2~ là tổng độ dài của hai đường đi ngắn hơn ~X~ ở trên trừ đi cạnh ~i~ nên ~T_1 + T_2 < 2X~. Khi đó ít nhất một trong hai số ~T_1~ và ~T_2~ phải bé hơn ~X~, tức là một trong hai đường đi

• ~1 \xrightarrow{\ P_3\ } A_i \xrightarrow{\ P_1\ } a_j \xrightarrow{\ P_4\ } B_i \xrightarrow{\ P_2\ } n~

• ~1 \xrightarrow{\ P_0\ } a_{j - 1} \xrightarrow{e_{j - 1}} a_j \xrightarrow{\ \ e_j\ \ } a_{j + 1} \xrightarrow{\ P_5\ } n~

có độ dài ngắn hơn ~X~. Nhưng khi đó tồn tại một đường đi ngắn hơn ~X~ mà không đi qua cạnh ~i~, mâu thuẫn với định nghĩa cạnh tốt ban đầu.

Vậy ta chỉ cần tìm các cạnh mà khi bỏ đi sẽ làm ~1~ và ~n~ mất tính liên thông. Đến đây ta có thể sử dụng Tarjan để tìm các cạnh cầu trong đồ thị ~H~, sau đó kiểm tra cùng điều kiện thứ hai.

Chú ý: Chỉ trong bài này, các cạnh mà khi bỏ đi sẽ làm ~1~ và ~n~ mất tính liên thông là các cạnh cầu, do tất cả các cạnh trong đồ thị ~H~ đều thuộc một đường đi nào đó từ ~1~ đến ~n~. Trong các đồ thị khác, có thể một cạnh là cạnh cầu, nhưng khi bỏ đi thì ~1~ và ~n~ vẫn có thể liên thông do cạnh đó không đóng góp vào việc kết nối hai đỉnh.

Độ phức tạp: ~O(m \cdot w_{max} + m \log m)~.

Subtask 6: Không có ràng buộc gì thêm.

Chú ý ở Subtask 5 ta phải kiểm tra xem có cách tăng để mọi đường đi lớn hơn hoặc bằng ~X~ hay không, nên giá trị True/False của việc kiểm tra là đơn điệu. Vì thế ta có thể sử dụng tìm kiếm nhị phân để tối ưu.

Độ phức tạp: ~O(m \log w_{max} + m \log m)~.

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ii pair<int,int>
const int N = 3e5+5;
int n,m;
struct edge {
    int v;
    int w;
    int id;
};
vector<edge> a[N];
struct vcl {
    int u;
    ll val;
    bool operator < (const vcl &o) const {
        return val > o.val;
    }
};
bool mini (ll &a, ll b) {
    if (a > b) {
        a = b;
        return true;
    }
    return false;
}
ll d[N],g[N];
void dijkstra (int st, ll *d) {
    for (int i=1; i<=n; i++) d[i]  =1e18;
    priority_queue<vcl> pq;
    pq.push({st,0ll});
    d[st] = 0ll;
    while (pq.size()) {
        vcl dak = pq.top();
        pq.pop();
        int u = dak.u; ll val = dak.val;
        if (val > d[u]) continue;
        for (auto v : a[u]) {
            if (mini(d[v.v],val+v.w)) {
                pq.push({v.v,d[v.v]});
            }
        }
    }
}
struct adak {
    int u,v;
    int w;
}e[N];
int value[N];
namespace sub4 {
    int vis[N];
    vector<edge> adj[N];
    int low[N],num[N],cnt;
    bool ok;
    ll val;
    int in[N];
    void dfs (int u, int p) {
        vis[u] = true;
        if (u == n) in[u] = true;
        for (auto cc : adj[u]) {
            int v = cc.v;
            int w = cc.w;
            if (vis[v]) continue;
            dfs(v,u);
            in[u] |= in[v];
        }           
    }
    void go (int u, int p) {
        num[u] = low[u] = ++cnt;
        for (auto cc : adj[u]) {
            int v = cc.v; int w = cc.w;
            int id = cc.id;
            if (v == p) continue;
            if (num[v]) low[u] = min (low[u],num[v]);
            else {
                go (v,u);
                low[u] = min (low[u],low[v]);
                if (low[v] >= num[v]) {
                    if (in[v] && d[u] + g[v] + value[id]>= val && d[v] + g[u] + value[id] >= val) {
                    //  cout << "cau "<< u << ' ' << v << "?\n";
                        ok = true;
                        return;
                    }
                }
            }
        }
    }
    bool check (ll mid) {
        ok = false;
        cnt = 0;
        val = mid;
        for (int i=1; i<=n; i++) {
            adj[i].clear();
            vis[i] = false;
            in[i] = false;
            num[i] = low[i] = 0;
        }
        for (int i=1; i<=m; i++) {
            int u = e[i].u, v = e[i].v, w = e[i].w;
            if (d[u] + w + g[v] < mid || d[v] + w + g[u] < mid) {
                adj[u].push_back({v,w,i});
                adj[v].push_back({u,w,i});
            }
        }
        dfs(1,0);
        go(1,0);
        return ok;
    }
    void solve () {
        dijkstra(n,g);
        dijkstra(1,d);
        vector<ll> adu;
        for (int i=1; i<=m; i++) {
            int u = e[i].u, v = e[i].v, w = e[i].w;
            adu.push_back(d[u] + w + g[v]);
            adu.push_back(d[v] + w + g[u]);
            adu.push_back(d[u] + value[i] + g[v]);
            adu.push_back(d[v] + value[i] + g[u]);
        }
        sort (adu.begin(),adu.end());
        adu.resize(unique(adu.begin(),adu.end())-adu.begin());
        ll l = 1, r = (int) adu.size() - 1, res = d[n];
        while (r >= l) {
            ll mid = (r+l) >> 1;
            if (check(adu[mid])) res = adu[mid], l = mid + 1;
            else r = mid - 1;
        }
        cout << res;
    }
}
signed main() {
    ios_base::sync_with_stdio(false);
    cin.tie(0);
    cin >> n >> m;
    for (int i=1; i<=m; i++) {
        int u,v,w; cin >> u >> v >> w;
        a[u].push_back({v,w,i});
        a[v].push_back({u,w,i});
        e[i].u = u, e[i].v = v, e[i].w = w;
    }
    int mx = 0;
    for (int i=m; i>=1; i--) {
        value[i] = e[i].w + mx;
        mx = max (mx,e[i].w);
    }
    sub4::solve();
}