Bedao OI Contest 7 - Đồ thị tăng
Xem dạng PDFQuân có một đồ thị hai chiều liên thông gồm ~n~ đỉnh và ~m~ cạnh, cạnh thứ ~i~ nối giữa đỉnh ~u_i~ với ~v_i~ và có trọng số là ~w_i~. Bảo thực hiện thao tác sau chính xác một lần lên đồ thị của Quân:
Chọn cạnh thứ ~i~ và cạnh thứ ~j~ (~i < j~) và gán ~w_i~ = ~w_i~ + ~w_j~.
Bảo muốn tối đa hoá đường đi ngắn nhất từ đỉnh ~1~ tới đỉnh ~n~ trên đồ thị mới này. Hãy giúp Bảo tính xem độ dài đường đi ngắn nhất từ đỉnh ~1~ tới đỉnh ~n~ lớn nhất có thể là bao nhiêu.
Input
Dòng đầu tiên chứa số nguyên dương ~n~ và ~m~ ~(1 \le n,m \le 3 \cdot 10^5).~
~m~ dòng tiếp theo, dòng thứ ~i~ chứa ba số nguyên ~u_i~, ~v_i~, ~w_i~ biểu thị cạnh nối thứ ~i~ ~(1 \le u_i, v_i \le n, 0 \le w_i \le 10^9).~
Output
In ra một số là kết quả của bài toán.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~10~ | ~n,m\le100~ |
| 2 | ~10~ | ~n,m \le 2000~ |
| 3 | ~10~ | ~m=n-1~ |
| 4 | ~20~ | ~w_i=1~ ~\forall~ i ~\in~ [1,~m~] |
| 5 | ~25~ | ~w_i \le 10~ ~\forall~ i ~\in~ [1,~m~] |
| 1 | ~25~ | Không có ràng buộc gì thêm |
Sample Input 1
6 8
1 2 2
1 3 4
2 3 1
3 5 3
2 5 3
2 6 3
5 6 2
6 4 1
Sample Output 1
8
Notes
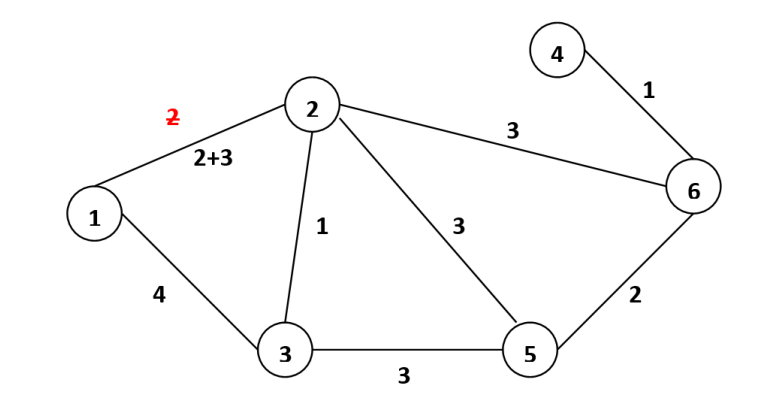
Bảo chọn cạnh ~(1, 2)~ và ~(2, 6)~ và gán trọng số cạnh ~(1, 2)~ thành ~2 + 3 = 5~.
Đường đi ngắn nhất: ~1 - 2 - 6~

Bình luận
Mấy bạn nhớ thêm freopen nha, để nhập xuất file
Bài này khó vc, sao dc có 0,01 điểm z
do có editorial đó bạn hihi