Quy hoạch động cái túi trên cây
Người viết:
- Nguyễn Tấn Minh - Trường Đại học Khoa học Tự nhiên, ĐHQG-HCM.
Reviewer:
- Nguyễn Quang Minh - Michigan State University.
- Võ Khắc Triệu - National University of Singapore.
Mở đầu
Đối với nhiều người theo đuổi Lập trình thi đấu, hai lớp bài toán quy hoạch động cái túi và quy hoạch động trên cây chắc hẳn là hai lớp bài toán vô cùng quen thuộc.
Bên cạnh đó, ta còn có dạng bài toán kết hợp ý tưởng quy hoạch động cái túi lên cấu trúc cây, cho ra đời lớp bài toán quy hoạch động cái túi trên cây. Đây tưởng chừng như một dạng bài tập rất hóc búa và đòi hỏi các thuật toán phức tạp. Tuy nhiên, chỉ với một vài lập luận tương đối đơn giản thì ta đã thấy được rằng, chỉ cần duyệt cây một cách khéo léo, ta đã có thể giải quyết bài toán quy hoạch động cái túi trên cây đơn giản hơn nhiều.
Trong mục Kỹ thuật thú vị của Tạp chí VNOI lần này, chúng ta sẽ cùng điểm qua các phân tích liên quan đến lớp bài toán quy hoạch động cái túi này.
Trường hợp chính
Bài toán: CEOI 2017 - Museum
Cho cây gồm ~n~ đỉnh (~1 \leq n \leq 10^4~), ~n - 1~ cạnh có trọng số cho biết thời gian di chuyển qua cạnh đó, và hai số nguyên ~k, x~. Tìm lộ trình tốn ít thời gian nhất để di chuyển từ ~x~ qua ~k~ đỉnh khác nhau kể cả ~x~ (kết thúc tại đỉnh bất kỳ).
Phân tích bài toán
Để đơn giản hóa bài toán, ta tạm thời biến đổi ràng buộc bài toán thành lộ trình xuất phát từ ~x~ phải quay về đỉnh ~x~.
Đặt gốc cây tại ~x~. Ta thấy rằng với mỗi cây con ~v_{x, i}~ của ~x~, ta cần thăm ~s_{x, i}~ đỉnh sao cho ~s_{x, 1} + s_{x, 2} + \dots + s_{x, t} = k - 1~. Hơn nữa, tập các đỉnh được thăm tạo thành một thành phần liên thông.
Từ đó, ta có ý tưởng đặt trạng thái quy hoạch động ~\texttt{dp}(u, j)~ là tổng thời gian để thăm ~j~ đỉnh của cây con gốc ~u~ và quay lại đỉnh ~u~. Dễ thấy ~j \leq \texttt{sz}[u]~ với ~\texttt{sz}[u]~ là kích thước của cây con gốc ~u~. Gọi ~v_1, v_2, \dots, v_t~ và ~w_1, w_2, \dots, w_t~ lần lượt là các đỉnh con của ~u~ và trọng số các cạnh nối tới chúng. Khi đó, ta có công thức truy hồi:
$$ \texttt{dp}(u, j) = \min_{s_1 + s_2 + \dots + s_t = j - 1} \left( \sum_{1 \leq i \leq t} \texttt{dp}(v_i, s_i) + [s_i \geq 1] \cdot 2w_i \right) $$
Nếu xem một cây con ~v_i~ là "một loại món đồ" và cây con ~u~ là "cái túi", ta có thể biến đổi chúng thành một bài toán quy hoạch động cái túi: Với mỗi loại món đồ, ta có thể chọn ~s_i~ cái với chi phí ~\texttt{dp}(v_i, s_i) + [s_i \geq 1] \cdot 2w_i~, cần chọn các món đồ sao cho tổng số lượng được chọn là ~j - 1~. Ở đây ~[X]~ là ký hiệu của Inverson bracket, mang giá trị ~1~ khi mệnh đề ~X~ đúng và ~0~ nếu ngược lại.
Để xử lý bài toán con trên, ta gọi ~\texttt{knap}(i, j)~ là tổng chi phí tối thiểu nếu chọn ~j~ món đồ ở ~i~ loại món đồ đầu tiên. Ta có công thức truy hồi
$$ \texttt{knap}(i, j) = \min_{0 \leq c \leq \texttt{sz}[v_i]} (\texttt{knap}(i - 1, j - c) + \texttt{dp}(v_i, c) + [c \geq 1] \cdot 2w_i) $$
Để tính mọi trạng thái ~(i, j)~, độ phức tạp của hàm quy hoạch động cái túi này là ~\mathcal{O}(\texttt{sz}[u]^2)~, dẫn đến độ phức tạp chung của bài toán lên đến ~\mathcal{O}(n^3)~. Tuy nhiên, nếu chỉ duyệt những trạng thái "có nghĩa" một cách khéo léo, độ phức tạp của thuật toán đã có thể giảm xuống ~\mathcal{O}(n^2)~!
Cải tiến & Phân tích độ phức tạp
Để ý rằng khi duyệt đến ~i~ cây con đầu tiên, ~v_1, v_2, v_3, \dots, v_i~, chỉ có các trạng thái ~\texttt{knap}(i, j)~ thỏa ~j \leq \texttt{sz}[v_1] + \texttt{sz}[v_2] + \dots + \texttt{sz}[v_i]~ mới có giá trị xác định, còn lại là các giá trị vô cực, không đóng góp vào công thức truy hồi. Do đó, để tiết kiệm tối đa số lần duyệt, ta có thể cài đặt quy hoạch động trên cây như sau:
int knap[2020], dp[2020][2020];
void dfs (int u, int p) {
// khởi tạo mảng knap[...]
// ...
int knapSize = 0;
for (int v : adj[u]) {
if (v == p) continue;
dfs(v, u);
for (int preTake = knapSize; preTake >= 0; preTake--)
for (int curTake = 0; curTake <= sz[v]; curTake++)
// tính knap[preTake + curTake] dựa trên
// knap[preTake] và dp[v][take]
knapSize += sz[v];
}
sz[u] = 1 + knapSize;
// cập nhật dp[u][...] dựa trên knap[...]
// ...
}
Để phân tích độ phức tạp, ta có thể mô hình hóa quá trình duyệt các cặp ~(\texttt{preTake}, \texttt{curTake})~ thành duyệt các cặp đỉnh ~(s_1, s_2)~ với ~s_1~ thuộc một trong các cây con trước đó ~v_1, v_2, \dots, v_{i-1}~ hoặc ~s_1 = u~, và ~s_2~ thuộc cây con hiện tại ~v_i~. Đặc biệt, các cặp ~(s_1, v_i)~ sẽ được tính 2 lần.
Cả hai mô hình duyệt đều có đúng ~(\texttt{knapSize} + 1) \cdot (\texttt{sz}[v] + 1)~ bước duyệt.
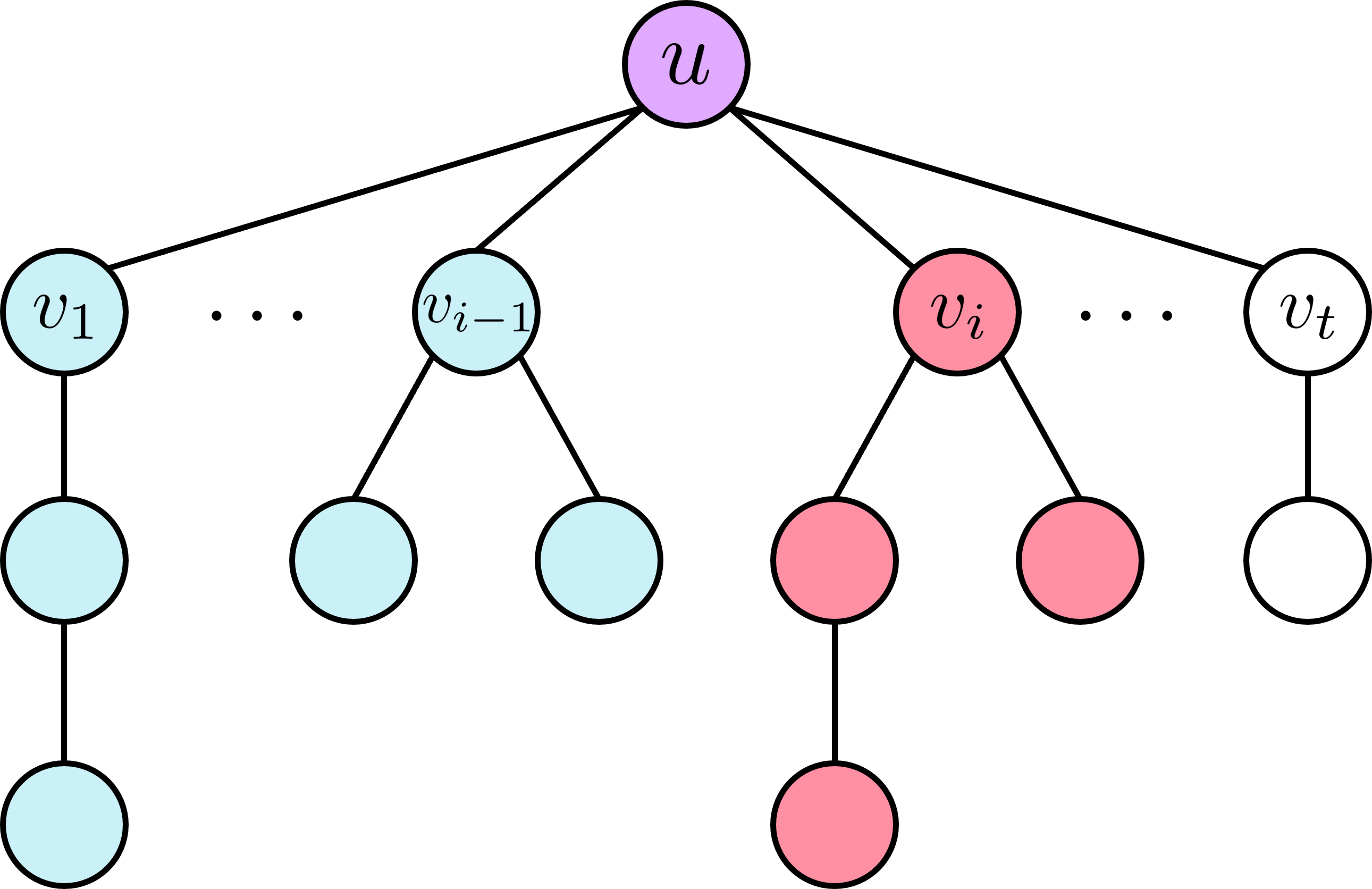
Ví dụ, ở hình trên, tại bước duyệt cây con ~v_i~, ta có thể hình dung việc duyệt các cặp ~(\texttt{preTake}, \texttt{curTake})~ giống như việc duyệt các cặp ~(s_1, s_2)~ sao cho ~s_1~ thuộc nhóm màu xanh/tím và ~s_2~ thuộc nhóm màu đỏ.
Một nhận xét quan trọng là hai đỉnh ~s_1, s_2~ chỉ sẽ được bắt cặp tại lượt DFS của đỉnh ~u~ thỏa ~\texttt{lca}(s_1, s_2) = u~. Do đó, với hai đỉnh ~z_1 < z_2~, dễ thấy tổng số lần duyệt của cặp ~(z_1, z_2)~ và ~(z_2, z_1)~ chỉ là tối đa ~2~ lần.
Tổng kết lại, số lần duyệt tối đa của cách cài đặt quy hoạch động như trên là:
$$ 2 \cdot C_n^2 = n \cdot (n - 1) = \mathcal{O}(n^2) $$
Có thể thấy, số lần duyệt tối đa thậm chí còn chưa đến ~n^2~!
Thuật toán
Quay lại bài toán ban đầu, ta gọi ~\texttt{dp}_0(u, j)~ và ~\texttt{dp}_1(u, j)~ lần lượt là tổng thời gian để thăm ~j~ đỉnh thuộc cây con ~u~ rồi quay về ~u~ (trạng thái 0) hoặc kết thúc ở một đỉnh bất kỳ là con của ~u~ (trạng thái 1). Khi đó, ta điều chỉnh công thức truy hồi thành:
$$ \begin{align*} \texttt{dp}_0(u, j) &= \min_{s_1 + s_2 + \dots + s_t = j - 1} \left( \sum_{1 \leq i \leq t} \texttt{dp}_0(v_i, s_i) + [s_i \geq 1] \cdot 2 w_i \right) \\ \texttt{dp}_1(u, j) &= \min_{\substack{s_1 + s_2 + \dots + s_t = j - 1 \\ b_1 + b_2 + \dots + b_t = 1}} \left( \sum_{1 \leq i \leq t} \texttt{dp}_{b_i}(v_i, s_i) + [s_i \geq 1] \cdot (2 - b_i) \cdot w_i \right) \end{align*} $$
Nói cách khác, với ~\texttt{dp}_0(u, j)~, mọi cây con sẽ được thăm rồi quay về ~u~. Với ~\texttt{dp}_1(u, j)~, ta chọn một cây con để kết thúc hành trình, các cây con còn lại sẽ được thăm rồi quay về ~u~. Việc thực hiện quy hoạch động cái túi sẽ diễn ra tương tự phần phân tích như trên. Như vậy, ta có lời giải quy hoạch động trong ~\mathcal{O}(n^2)~.
Code tham khảo
#include <bits/stdc++.h>
using namespace std;
using pii = pair<int,int>;
const int mn = 1e4 + 1;
int dp[2][mn][mn], knap[2][mn], sz[mn], n, k, x;
vector<pii> adj[mn];
void dfs (int u, int p) {
// gọi DFS và tính kích thước cây con (sz[u])
sz[u] = 1;
for (auto [v, w] : adj[u])
if (v != p) dfs(v, u), sz[u] += sz[v];
// khởi tảo mảng knap[...]
knap[0][0] = knap[1][0] = 0;
for (int i = 1; i <= sz[u]; i++)
knap[0][i] = knap[1][i] = INT_MAX;
// chạy DP Knapsack trên các cây con v[1], v[2], v[3],..., v[t]
int knapSize = 0;
for (auto [v, w] : adj[u]) {
if (v == p) continue;
for (int preTake = knapSize; preTake >= 0; preTake--) {
for (int curTake = 1; curTake <= sz[v]; curTake++) {
int sum = preTake + curTake;
knap[0][sum] = min(knap[0][sum], knap[0][preTake] + dp[0][v][curTake] + 2 * w);
knap[1][sum] = min(knap[1][sum], knap[0][preTake] + dp[1][v][curTake] + w);
knap[1][sum] = min(knap[1][sum], knap[1][preTake] + dp[0][v][curTake] + 2 * w);
}
}
knapSize += sz[v];
}
// trả các giá trị từ hàm knap[...] sang dp[...]
for (int i = 0; i < sz[u]; i++)
dp[0][u][i + 1] = knap[0][i], dp[1][u][i + 1] = knap[1][i];
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int n, k, x; cin >> n >> k >> x;
for (int i = 1; i < n; i++) {
int a, b, c; cin >> a >> b >> c;
adj[a].emplace_back(b, c);
adj[b].emplace_back(a, c);
}
dfs(x, -1);
cout << dp[1][x][k] << "\n";
return 0;
}
Trường hợp có cận trên cố định
Bài toán: VNOJ - Bài toán cái túi trên cây
Cho cây gồm ~n~ đỉnh (~1 \leq n \leq 10^5~) và một số nguyên ~k~ (~1 \leq k \leq 200~). Các đỉnh trên cây được gán một trọng số được cho bởi dãy ~a_1, a_2, a_3, \dots, a_n~ (~-10^9 \leq a_i \leq 10^9~).
Tìm một thành phần liên thông gồm đúng ~k~ đỉnh trên cây sao cho tổng trọng số của các đỉnh thuộc thành phần liên thông đó là lớn nhất.
Phân tích bài toán
Tương tự với bài toán ở trên, ta cũng định nghĩa hàm quy hoạch động ~\texttt{dp}(u, j)~ là tổng trọng số tối đa của thành phần liên thông gồm đỉnh ~u~ và các nút con của ~u~. Công thức truy hồi của quy hoạch động là:
$$ \texttt{dp}(u, j) = \max_{s_1 + s_2 + \dots + s_t = j - 1} \left( \sum_{1 \leq i \leq t} \texttt{dp}(v_i, s_i) \right) + a_u $$
Ta cũng coi các cây con ~v_1, v_2, \dots, v_t~ như những "món đồ" trong bài toán quy hoạch động cái túi và tính hàm ~\texttt{knap}(i, j)~ như sau:
$$ \texttt{knap}(i, j) = \max_{0 \leq c \leq \min(k, \texttt{sz}[v_i])} ( \texttt{knap}(i - 1, j - c) + \texttt{dp}(v_i, c)) $$
Thoạt nhìn như thuật toán có độ phức tạp ~\mathcal{O}(nk^2)~ hay ~\mathcal{O}(n^2)~. Nhưng cũng tương tự trường hợp như trên, nếu duyệt một cách khéo léo, ta có thể giảm độ phức tạp xuống ~\mathcal{O}(nk)~!
Cải tiến & Giảm độ phức tạp
Khi duyệt để tính hàm ~\texttt{knap}(i, j)~, ta giới hạn các giá trị ~\texttt{preTake}~ bởi ~\min(\texttt{knapSize}, k)~ và các giá trị ~\texttt{curTake}~ bởi ~\min(\texttt{sz}[v_i], k - \texttt{preTake})~. Nói cách khác, ta có thể cài đặt quy hoạch động như sau:
long long knap[202], dp[100'002][202];
int k;
void dfs (int u, int p) {
// khởi tạo mảng knap[...]
// ...
int knapSize = 0;
for (int v : adj[u]) {
if (v == p) continue;
dfs(v, u);
for (int preTake = min(knapSize, k); preTake >= 0; preTake--)
for (int curTake = 0; curTake <= min(sz[v], preTake); curTake++)
// tính knap[preTake + curTake] dựa trên
// knap[preTake] và dp[v][take]
knapSize += sz[v];
}
sz[u] = 1 + knapSize;
// cập nhật dp[u][...] dựa trên knap[...]
// ...
}
Để phân tích độ phức tạp, ta lại sử dụng ý tưởng biến đổi mô hình for như trên thành duyệt các cặp đỉnh ~(s_1, s_2)~ có ~\texttt{lca}(s_1, s_2) = u~. Tuy nhiên, trong trường hợp số lượng đỉnh có thể chọn làm ~s_1~ hoặc ~s_2~ là nhiều hơn ~k + 1~, ta sẽ ưu tiên chọn ~s_1~ có thứ tự thăm DFS muộn nhất và ~s_2~ có thứ tự thăm DFS sớm nhất. Tương tự với phân tích ở phần trước, nếu đã chọn đủ ~\texttt{sz}[v_i]~ đỉnh làm ~s_2~, ta quay về chọn ~v_i~ làm đỉnh thứ ~\texttt{sz}[v_i] + 1~.
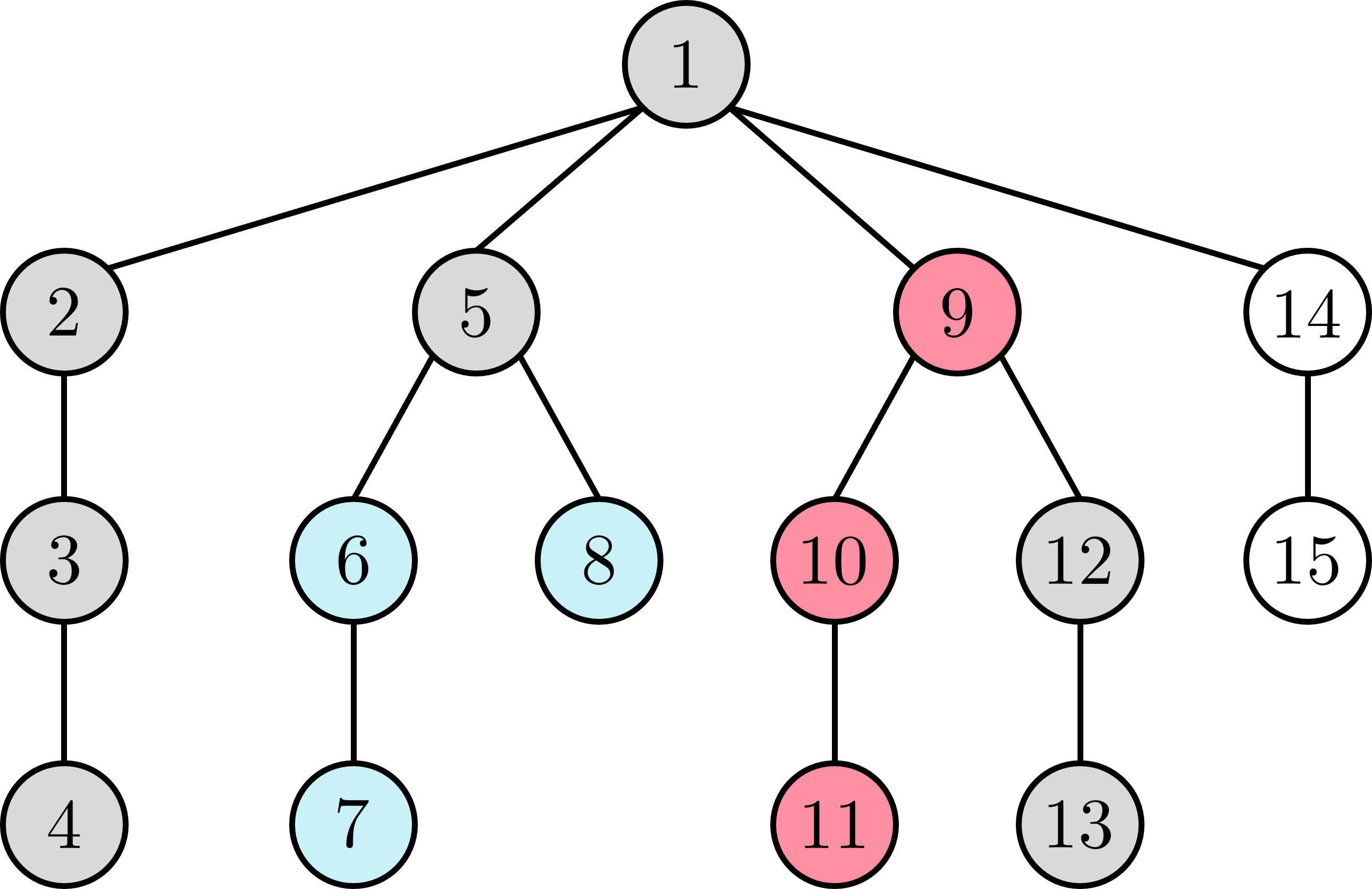
Ví dụ, với trường hợp trên, khi duyệt đến ~u = 1~ và ~v_i = 9~, với ~k = 2~, ta chỉ chọn các đỉnh ~6, 7, 8~ làm ~s_1~ và ~9, 10, 11~ làm ~s_2~. Để dễ phân tích, các đỉnh đã được đánh số theo thứ tự DFS.
Một nhận xét vô cùng quan trọng đó là khoảng cách của ~s_1, s_2~ trên dãy thứ tự DFS với cách chọn này sẽ là không quá ~2k + 1~. Trên thực tế, với điều kiện ~\texttt{preTake} + \texttt{curTake} \leq k~, ta còn có thể kết luận rằng khoảng cách thực sự là không quá ~k~.
Từ đó, ta cũng lập luận được rằng một cặp ~(s_1, s_2)~ xuất hiện không quá ~2~ lần, cộng với việc khoảng cách của ~s_1, s_2~ trên dãy thứ tự DFS là không quá ~k~, ta có thể kết luận rằng với mọi ~s_1~, ta chỉ có tối đa ~2k~ đỉnh có thể chọn làm ~s_2~.

Nói cách khác, số lần duyệt tối đa trong hàm quy hoạch động như trên là:
$$ 2nk = \mathcal{O}(nk) $$
Code tham khảo
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
using pl = pair<ll,ll>;
using pii = pair<int,int>;
using tpl = tuple<int,int,int>;
#define all(a) a.begin(), a.end()
#define filter(a) a.erase(unique(all(a)), a.end())
const int mn = 1e5 + 5;
ll knap[202], dp[mn][202];
int a[mn], sz[mn], n, k;
vector<int> adj[mn];
void dfs (int u, int p) {
// tiền xử lý và khởi tạo mảng knap[...]
sz[u] = 1;
for (int v : adj[u])
if (v != p) dfs(v, u), sz[u] += sz[v];
for (int i = 1; i <= min(sz[u], k); i++) knap[i] = LLONG_MIN;
knap[0] = 0;
// thực hiện QHĐ cái túi trên các cây con của u
int knapSize = 0;
for (int v : adj[u]) {
if (v == p) continue;
for (int preTake = min(k, knapSize); preTake >= 0; preTake--)
for (int curTake = 0; curTake <= min(k - preTake, sz[v]); curTake++)
knap[preTake + curTake] = max(knap[preTake + curTake], knap[preTake] + dp[v][curTake]);
knapSize += sz[v];
}
// cập nhật dp[u][...] dựa trên knap[...]
for (int i = 0; i < min(sz[u], k); i++) dp[u][i + 1] = a[u] + knap[i];
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> k;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i < n; i++) {
int a, b; cin >> a >> b;
adj[a].push_back(b);
adj[b].push_back(a);
}
dfs(1, -1);
ll ans = LLONG_MIN;
for (int i = 1; i <= n; i++)
if (sz[i] >= k) ans = max(ans, dp[i][k]);
cout << ans << "\n";
return 0;
}
Công thức biến thể
Bên cạnh đó, nếu công thức quy hoạch động cái túi có dạng:
$$ \texttt{dp}(u, j) = \min_{\substack{s_1 \neq s_2 \\ j_1 + j_2 = j}} (\texttt{dp}(s_1, j_1) + \texttt{dp}(s_2, j_2)) $$
Ta cũng có thể thực hiện quy hoạch động trong ~\mathcal{O}(n^2)~ (không có cận trên cố định) và ~\mathcal{O}(nk)~ (có cận trên ~k~ cố định). Phần chứng minh có thể được tìm thấy tại đây và tại đây.
Bài tập áp dụng
- CEOI 2017, Museum
- COCI 2019, Dzumbus
- Codeforces Round 419, C, Karen and Supermarket
- Codeforces Testting Round 10, D, Berland Federalization
- AtCoder Beginner Contest 207, F, Tree Patrolling
- Codefroces Round 607, D, Miss Punyverse
Đóng góp từ cộng đồng
📌 Các bạn cũng có thể đóng góp bằng cách gửi bài viết và câu hỏi cho VNOI qua: Form
📌 Phần thưởng dành cho những đóng góp xuất sắc từ cộng đồng: lựa chọn một bộ merch độc quyền của VNOI gồm sổ, bút và sticker, hoặc nhận tiền nhuận bút. Ngoài ra, các bạn có nhiều đóng góp sẽ được nhận thêm áo VNOI.
Bình luận
Hay quá