Tạp chí VNOI - Số 1: Bài viết học thuật

Giải quyết bài toán LCA bằng DSU

Tác giả:

Võ Đức Đoàn - THPT Chuyên Nguyễn Tất Thành, Quãng Ngãi.

Reviewer:

Nguyễn Tiến Mạnh - Đại học Bách khoa Hà Nội.
Nguyễn Tấn Minh - Trường Đại học Khoa học Tự nhiên, ĐHQG-HCM.
Nguyễn Minh Hiển - Trường Đại học Công nghệ, ĐHQGHN.

Bài toán lowest common ancestor (gọi tắt là LCA) là một bài toán kinh điển, yêu cầu ta tìm tổ tiên chung gần nhất của hai đỉnh trên một cây. Các bạn có thể đã quen thuộc với các phương pháp giải quyết bài toán LCA như sử dụng nâng nhị phân hoặc RMQ.

Các phương pháp trên tuy rất tối ưu trong những trường hợp cụ thể, nhưng nếu số lượng đỉnh trên cây (~n~) và số lượng truy vấn (~m~) rất lớn thì sẽ không hiệu quả.

Để giải quyết những trường hợp trên, ta sử dụng thuật toán offline tìm LCA của Tarjan. Đây là một ứng dụng của cấu trúc dữ liệu (gọi tắt là CTDL) DSU, có thể giải quyết bài toán LCA với độ phức tạp rất nhanh: ~\mathcal{O}(n + m)~.

Thuật toán offline tìm LCA của Tarjan

Thuật toán offline tìm LCA của Tarjan, đúng như tên gọi của nó, là một thuật toán offline, tức là thuật toán phải biết trước được rằng nó sẽ phải tìm LCA của các cặp đỉnh nào.

Trước tiên, thuật toán sẽ tạo ~n~ tập hợp, mỗi tập hợp sẽ chứa một đỉnh trên cây. Sau đó, thuật toán duyệt cây bằng DFS. Với mỗi đỉnh ~u~, ta đánh dấu đỉnh ~u~ là đã được duyệt qua. Sau đó, ta thực hiện ~2~ quy trình chính:

Duyệt cây: với mỗi đỉnh con ~v~ của ~u~, ta duyệt cây con gốc ~v~ và thực hiện hợp hai tập hợp chứa hai đỉnh ~u, v~. Lưu ý rằng phần tử đại diện của tập hợp chứa đỉnh ~u~ bất kì là đỉnh gần đỉnh gốc nhất.
Xử lí truy vấn: với mỗi truy vấn ~(u, v)~ chứa đỉnh ~u~, nếu đỉnh ~v~ đã được duyệt qua, ta tính được LCA của truy vấn là phần tử đại diện của tập hợp chứa đỉnh ~v~.

Giả sử ta có cây sau, và ta cần tìm LCA của hai cặp đỉnh ~(4, 5)~ và ~(5, 6)~.

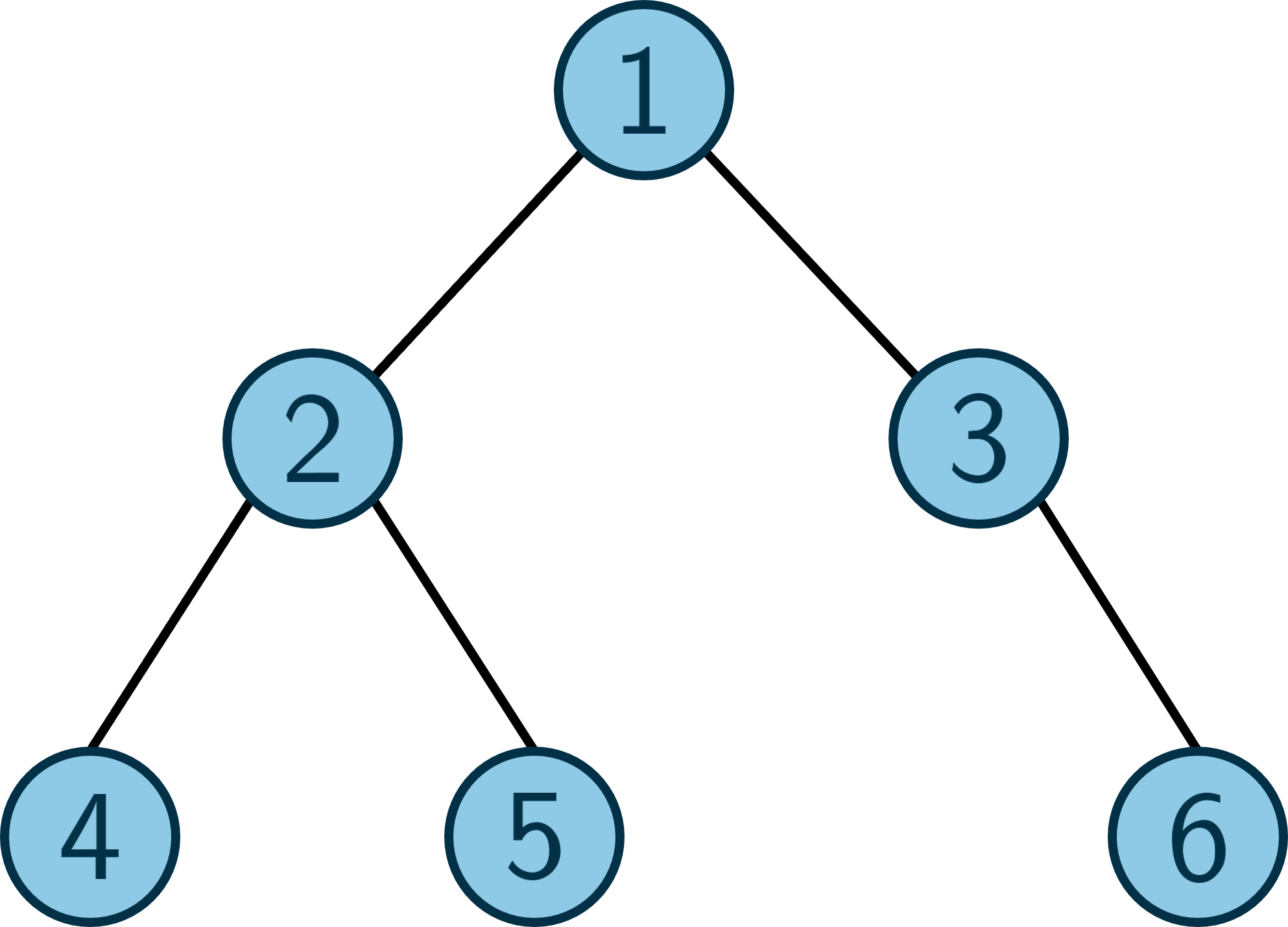OLCA_init )

Khi duyệt DFS đến đỉnh ~5~, cây sẽ có dạng sau: các đỉnh màu xanh dương là các đỉnh chưa được duyệt còn các đỉnh màu xanh lục là các đỉnh đã thăm duyệt, các đỉnh nằm trong mỗi ô có đường màu đỏ là các đỉnh thuộc cùng một tập hợp.

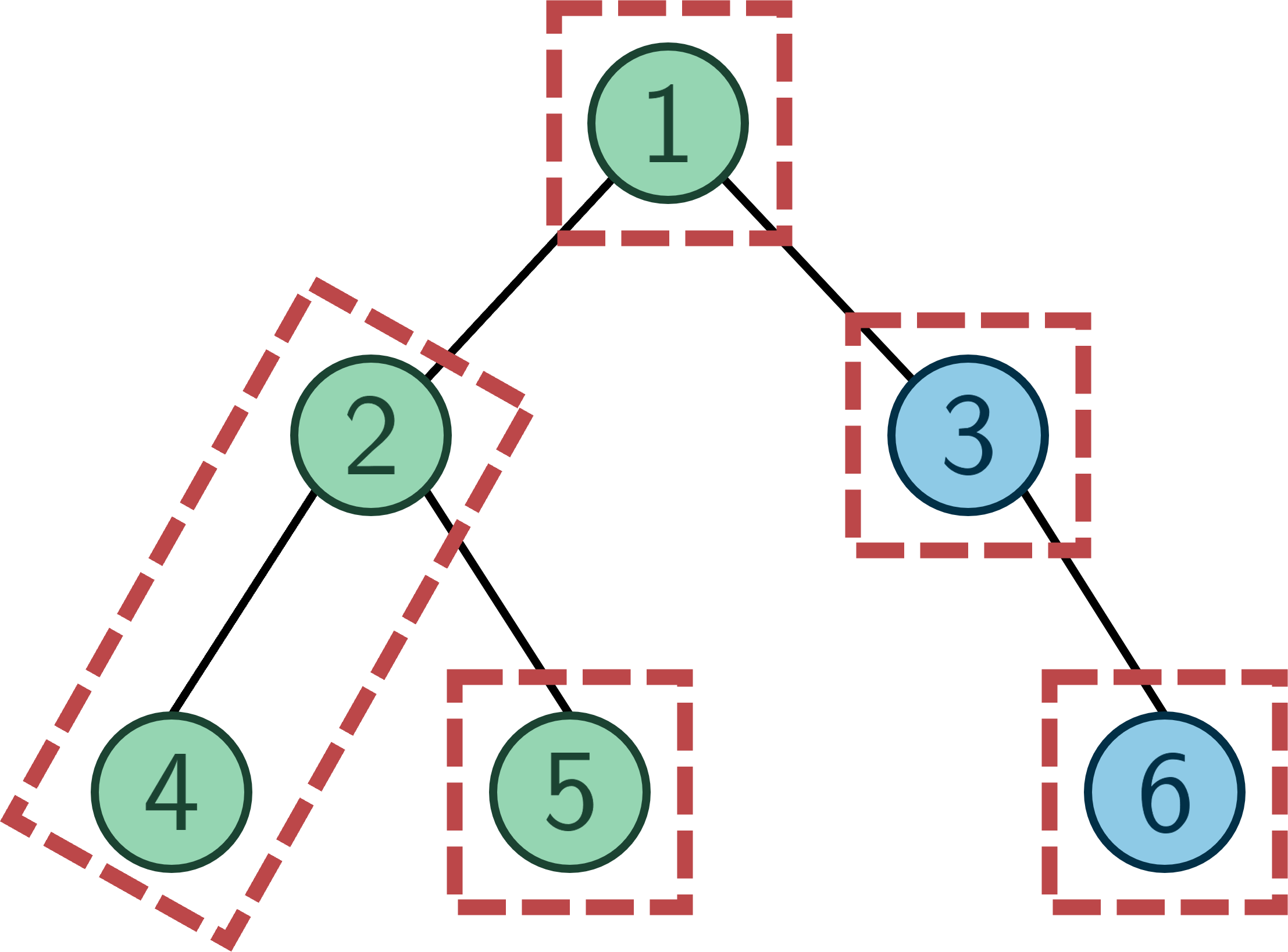
OLCA<em>4</em>5

Ta có phần tử đại diện của tập hợp chứa đỉnh ~4~ là đỉnh ~2~ nên LCA của ~(4,5)~ sẽ là đỉnh ~2~.

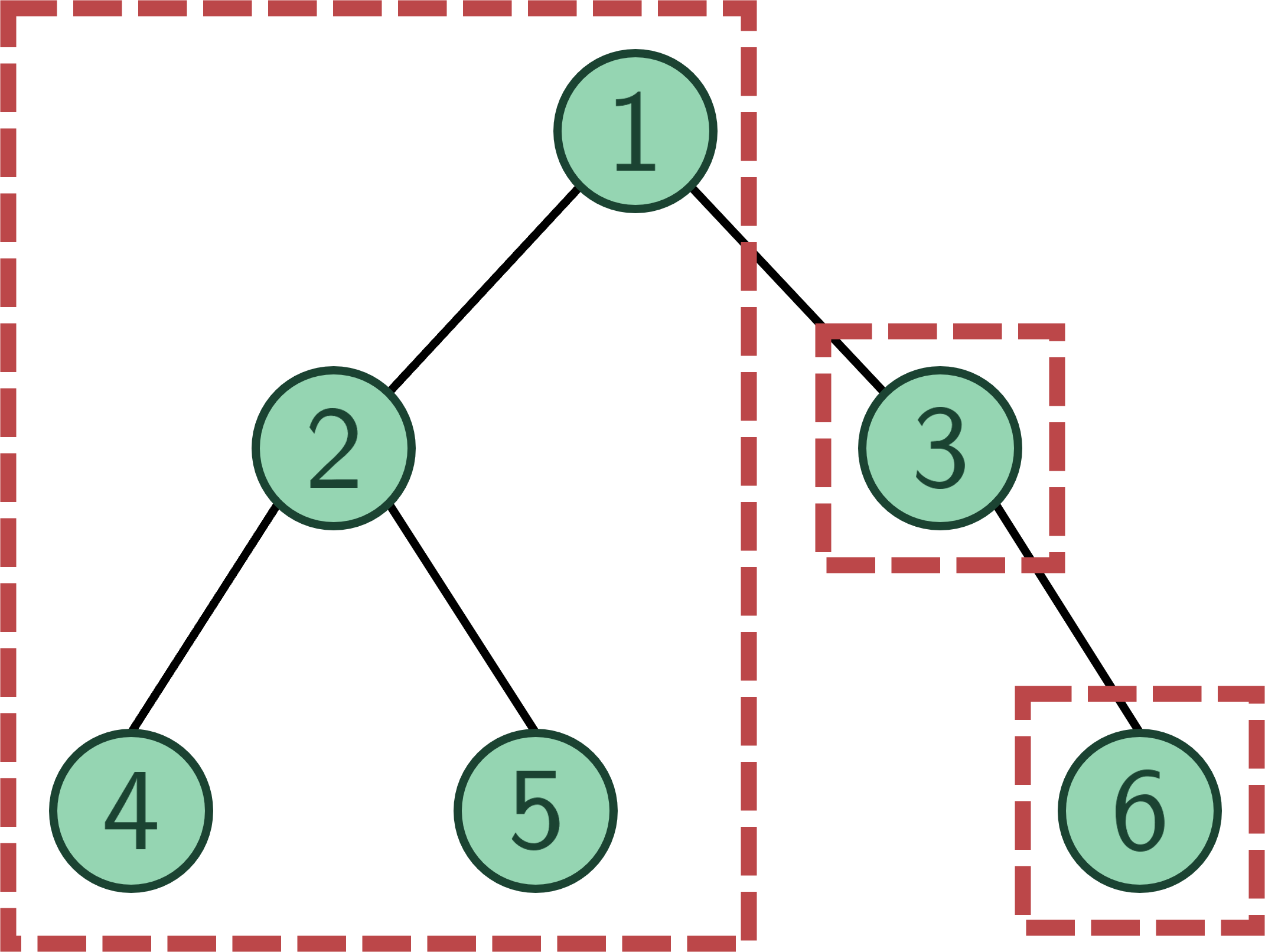
OLCA<em>5</em>6

Cũng với lập luận tương tự, khi duyệt tới đỉnh ~6~, ta có LCA của ~(5, 6)~ sẽ là đỉnh ~1~.

Thông thường, các cách cài đặt DSU ở trên sẽ không đảm bảo việc sau khi hợp hai tập hợp, phần tử đại diện của tập hợp chứa đỉnh ~u~ sẽ là đỉnh gần gốc nhất. Để khắc phục điều này, ta cần một biến ancestor để khắc phục điều này. ancestor của một đỉnh ~u~ là đỉnh gần gốc nhất trong tất cả các đỉnh nằm trong tập hợp chứa đỉnh ~u~. Ở phần duyệt các cây con của ~u~, sau khi hợp hai tập hợp, Ta sẽ gán ancestor của đỉnh đại diện là đỉnh gần gốc nhất, ở đây là đỉnh ~u~. Đoạn code dưới đây thực hiện điều này có dạng: ancestor[dsu.find(u)] = u.

// CTDL DSU
struct UnionFind{ 
    vector<int> p;
    UnionFind(int n) : p(n, -1) { }
    int find(int u) { return p[u] < 0 ? u : p[u] = find(p[u]); }             
    bool isSameSet(int u, int v) { return find(u) == find(v); }   
    bool Union(int u, int v) {                                    
        u = find(u);                                              
        v = find(v);                                              
        if (u == v) return 0;
        if(p[u] > p[v]) swap(u, v);
        p[u] += p[v];
        p[v] = u;
        return 1;
    }
} dsu(N);
vector<int> adj[N]; // cây
vector<pair<int, int>> queries; // các truy vấn
int ancestor[N]; // đỉnh gần gốc nhất trong tập hợp chứa đỉnh u
vector<int> qry[N]; // truy vấn sau tiền xử lí
bitset<N> vst; // đỉnh đã được duyệt hay chưa

void OLCA(int u, int p){
    vst[u] = 1; // đã thăm đỉnh u
    ancestor[u] = u;

    // duyệt cây
    for(int v : adj[u]){
        if(v == p) continue;
        OLCA(v, u); // xử lí cây con
        dsu.Union(u, v); // Union tập hợp chứa đỉnh cha và tập hợp chứa đỉnh con
        ancestor[dsu.find(u)] = u;
    }

    // xử lí truy vấn
    for(int v : qry[u]){
        if(vst[v]){
            cout << "LCA(" << u << ", " << v << "): " << ancestor[dsu.find(v)] << '\n';
        }
    }
}

void lca(){
    // tiền xử lí các truy vấn
    for (auto [u, v] : queries){
        qry[u].push_back(v);    
        qry[v].push_back(u);    
    }

    // các đỉnh được đánh số từ 0 đến n - 1
    OLCA(0, -1);
}

Phân tích thuật toán

Có lẽ điều làm bạn lăn tăn nhất về thuật toán này chính là phần in ra LCA của cặp đỉnh ~(u, v)~.

Giả sử ~LCA(u, v) = w~, ta có thể thấy: Khi ta duyệt đỉnh ~w~, hai đỉnh ~u~, ~v~ sẽ nằm trong hai cây con khác nhau của đỉnh ~w~.

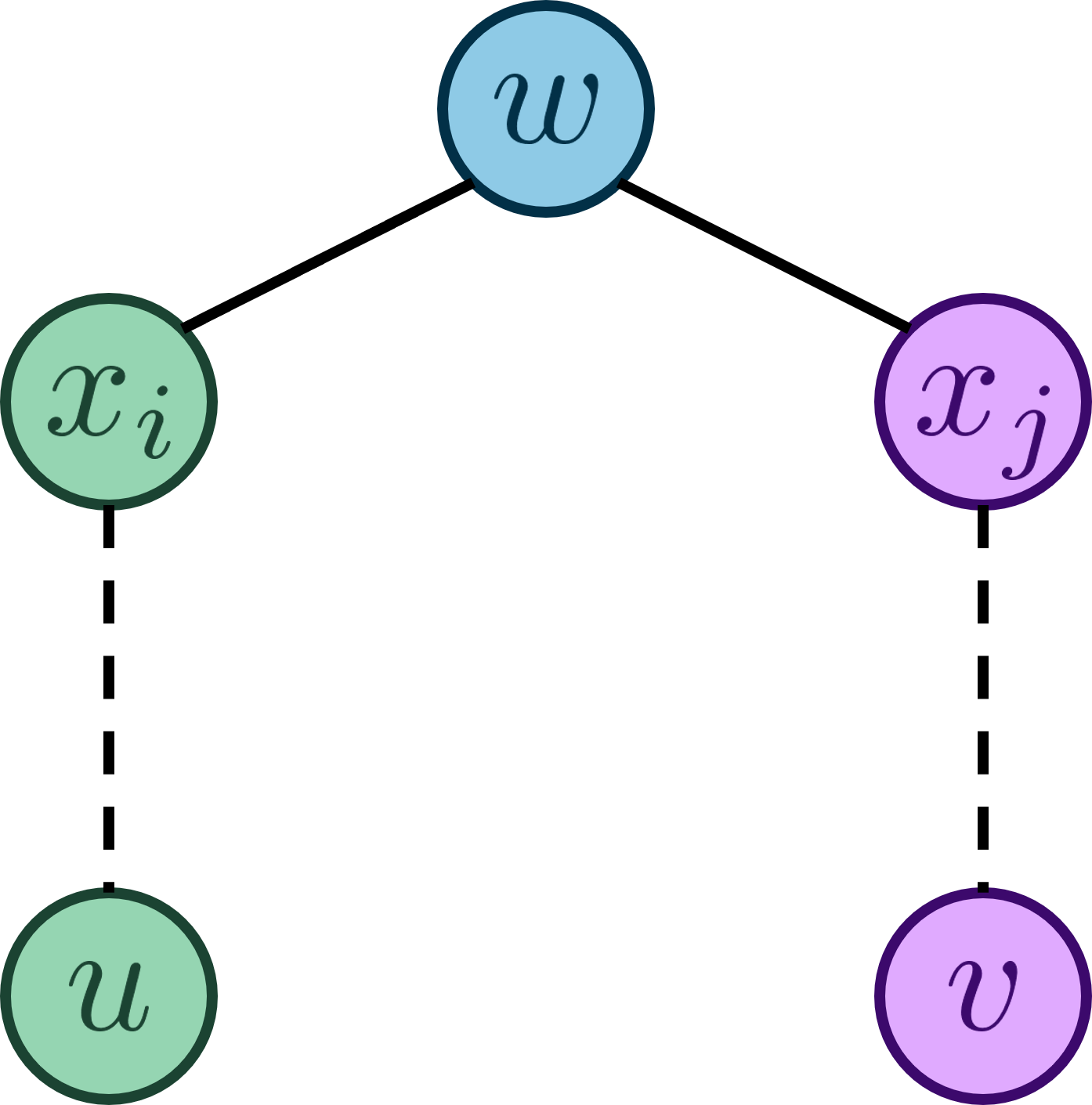
lca(u,v) = w

Sau khi duyệt cây con của ~w~ chứa đỉnh ~u~ (giả sử cây con chứa đỉnh ~u~ được duyệt trước), toàn bộ các đỉnh của cây con sẽ chỉ đến đỉnh ~w~ là đỉnh đại diện của tập hợp chứa các đỉnh ấy cho tới khi chương trình duyệt xong đỉnh ~w~. Khi này, lúc duyệt sang cây con chứa đỉnh ~v~, đỉnh đại diện của tập hợp chứa đỉnh ~u~ (tức là đỉnh ~w~) sẽ là LCA của cặp đỉnh ~(u, v)~.

Sử dụng lập luận trên, ta cũng có thể kết luận được rằng việc in ~LCA(u, v)~ của truy vấn ~(u, v)~ chỉ xảy ra đúng một lần mặc dù cặp truy vấn sẽ được xét ~2~ lần trong thuật toán.

Phân tích độ phức tạp

Quá trình duyệt cây có độ phức tạp ~\mathcal{O}(n)~. Với mỗi đỉnh, ta duyệt các truy vấn tổng cộng là ~2m~ lần nên có độ phức tạp ~\mathcal{O}(m)~. Độ phức tạp của DSU rất nhỏ (~\alpha(n)~ cho các thao tác find, union với kĩ thuật nén đường đi và union theo thứ hạng/kích thước) nên ta cho nó bằng ~\mathcal{O}(1)~.

Độ phức tạp của thuật toán bằng ~\mathcal{O}(n + m)~.

So sánh với các thuật toán khác

Thuật toán offline tìm LCA của Tarjan có thể nói là thuật toán tìm LCA nhanh nhất khi so với các thuật toán ta thường sử dụng trong lập trình thi đấu.

Thuật toán/kĩ thuật	Tiền xử lí	Xử lí từng truy vấn	Tổng độ phức tạp	Bộ nhớ
Nâng nhị phân	~\mathcal{O}(n\log{n})~	~\mathcal{O}(\log{n})~	~\mathcal{O}(n\log{n} + m\log{n})~	~\mathcal{O}(n\log{n})~
Nâng nhị phân bộ nhớ ~\mathcal{O}(n)~	~\mathcal{O}(n)~	~\mathcal{O}(\log{n})~	~\mathcal{O}(n + m\log{n})~	~\mathcal{O}(n)~
RMQ (bảng thưa)	~\mathcal{O}(n\log{n})~	~\mathcal{O}(1)~	~\mathcal{O}(n\log{n} + m)~	~\mathcal{O}(n\log{n})~
RMQ (segment tree)	~\mathcal{O}(n)~	~\mathcal{O}(\log{n})~	~\mathcal{O}(n + m\log{n})~	~\mathcal{O}(n)~
HLD	~\mathcal{O}(n)~	~\mathcal{O}(\log{n})~	~\mathcal{O}(n + m\log{n})~	~\mathcal{O}(n)~
Tarjan	~\mathcal{O}(n + m)~	~\mathcal{O}(1)~	~\mathcal{O}(n + m)~	~\mathcal{O}(n + m)~

Tuy nhiên, trên thực tế, nếu dữ liệu nhập không đủ lớn, thuật toán của Tarjan sẽ chậm hơn do những hạn chế về việc cài đặt thuật toán như việc gọi các hàm đệ quy liên lục như hàm OLCA và hàm dsu.find.

Tổng kết

Thuật toán offline tìm LCA của Tarjan là một thuật toán giúp ta giải quyết bài toán tìm LCA một cách nhanh chóng và hiệu quả. Thuật toán cũng là một ứng dụng của CTDL DSU mà nhiều người không hề hay biết.

Luyện tập

Đóng góp từ cộng đồng

📌 Các bạn cũng có thể đóng góp bằng cách gửi bài viết và câu hỏi cho VNOI qua: Form

📌 Phần thưởng dành cho những đóng góp xuất sắc từ cộng đồng: lựa chọn một bộ merch độc quyền của VNOI gồm sổ, bút và sticker, hoặc nhận tiền nhuận bút. Ngoài ra, các bạn có nhiều đóng góp sẽ được nhận thêm áo VNOI.