Kỳ thi Học sinh giỏi Quốc gia 2025 - Ngày 2
Điểm: 7
Một trường THPT chuyên đang tổ chức trò chơi tập thể cho ~M~ học sinh lớp chuyên Toán đánh số từ 1 đến ~M~ và ~L~ học sinh lớp chuyên Văn đánh số từ ~1~ đến ~L~. Trên sân, có ~N~ vị trí cách đều nhau đã được đánh dấu sẵn, các vị trí được đánh số từ ~1~ đến ~N~ tạo thành một vòng tròn:
Vị trí thứ ~1~ kề với vị trí thứ ~2~ và thứ ~N~;
Vị trí thứ ~i~ ~(2 \le i \le N-1)~ kề với vị trí thứ ~i-1~ và thứ ~i+1~;
Vị trí thứ ~N~ kề với vị trí thứ ~N-1~ và vị trí ~1~.
Ban đầu ~M+L~ học sinh đứng ở các vị trí sao cho không có ~2~ học sinh nào đứng cùng một vị trí. Học sinh thứ ~u~ của lớp chuyên Toán đứng ở vị trí ~P_u (1 \le u \le M)~, học sinh thứ ~v~ của lớp chuyên Văn đứng ở vị trí ~Q_v (1 \le v \le L)~. Mỗi bước, học sinh có thể di chuyển sang một trong ~2~ vị trí kề với vị trí đang đứng. Lưu ý, trong quá trình di chuyển, một vị trí có thể có nhiều hơn một học sinh. Các thầy cô muốn xác định vị trí tập trung của từng bạn sao cho:
Vị trí tập trung của ~M~ học sinh lớp chuyên Toán là ~M~ vị trí liên tiếp trên vòng tròn;
Vị trí tập trung của ~L~ học sinh lớp chuyên Văn là ~L~ vị trí liên tiếp trên vòng tròn;
Không có ~2~ học sinh nào đứng cùng một vị trí.
Yêu cầu: Hãy giúp các thầy cô xác định vị trí tập trung của các học sinh sao cho tổng số bước phải di chuyển của tất cả học sinh là nhỏ nhất.
Input
Vào từ file văn bản CYCLE.INP: Dòng đầu chứa một số nguyên ~T~ là số lượng trường hợp test ~(1 \le T \le 10^5)~. Tiếp theo ~T~ nhóm dòng, mỗi nhóm dòng mô tả một trường hợp test như sau:
Dòng thứ nhất chứa ~3~ số nguyên dương ~N, M~ và ~L (2 \le M + L \le N \le 10^5)~.
Dòng thứ hai chứa ~M~ số nguyên dương ~P_1, P_2, \ldots, P_M (1 \le P_1, P_2, \ldots, P_M \le N)~.
Dòng thứ ba chứa ~L~ số nguyên dương ~Q_1, Q_2, \ldots, Q_L (1 \le Q_1, Q_2, \ldots, Q_L \le N)~.
Dữ liệu đảm bảo tổng các số ~N~ trong một file dữ liệu vào không vượt quá ~2 \times 10^5~. Các số trên cùng một dòng cách nhau bởi dấu cách.
Output
Ghi ra file văn bản CYCLE.OUT:
- Gồm ~T~ dòng, mỗi dòng chứa một số nguyên duy nhất là tổng số bước di chuyển nhỏ nhất của tất cả học sinh tương ứng với trường hợp test trong dữ liệu vào.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~10\%~ | ~N \le 10; T \le 10.~ |
| 2 | ~15\%~ | ~N \le 500; 1 \le P_1, P_2, \ldots, P_M \lt \frac{N}{2}; 1 \le Q_1, Q_2, \ldots, Q_L \lt \frac{N}{2}; T \le 10.~ |
| 3 | ~15\%~ | ~N \le 5000; 1 \le P_1, P_2, \ldots, P_M \lt \frac{N}{2}; 1 \le Q_1, Q_2, \ldots, Q_L \lt \frac{N}{2}; T \le 10.~ |
| 4 | ~20\%~ | ~N \le 5000; T \le 10.~ |
| 5 | ~20\%~ | ~1 \le P_1, P_2, \ldots, P_M \lt \frac{N}{2}; 1 \le Q_1, Q_2, \ldots, Q_L \lt \frac{N}{2}; T \le 10.~ |
| 6 | ~20\%~ | Không có ràng buộc nào thêm. |
Sample Input 1
1
12 6 4
1 3 5 7 9 11
2 12 8 4
Sample Output 1
15
Notes
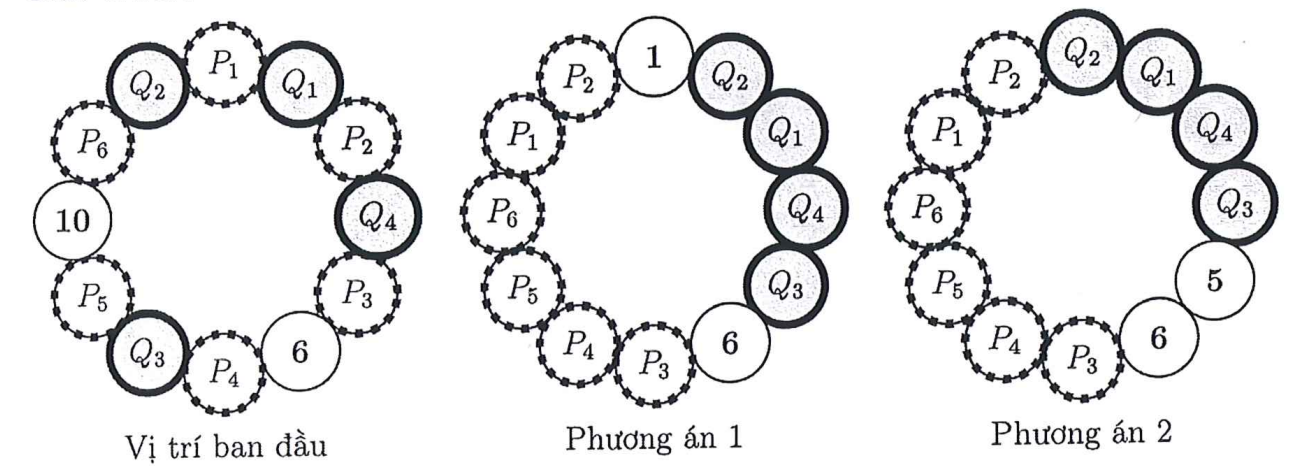
Trong phương án ~1~, số bước di chuyển của các học sinh chuyên Văn lần lượt là: ~1,2,3,0~; số bước di chuyển của các học sinh chuyên Toán lần lượt là: ~2,3,2,1,0,1~.
Trong phương án ~2~, số bước di chuyển của các học sinh chuyên Văn lần lượt là: ~0,1,4,1~; số bước di chuyển của các học sinh chuyên Toán lần lượt là: ~2,3,2,1,0,1~.
Cả hai phương án đều tối ưu và đều có tổng số bước là ~15~.
Điểm: 7
Với niềm đam mê về các bài toán trên dãy số của mình, hôm nay thầy giáo Lê nghiên cứu bài toán trên hai dãy số ~A~ và ~B~.
Dãy ~A~ gồm các số tự nhiên sắp xếp tăng dần từ 1 tới ~10^9~. Dãy ~B~ chỉ gồm duy nhất một số ~0~. Thầy Lê lần lượt đưa ra ~Q~ yêu cầu, mỗi yêu cầu thuộc một trong 3 loại sau:
Loại 1: Cho hai số ~X~ và ~K~, yêu cầu cắt ~K~ số đầu tiên của dãy ~A~, ghép vào ngay sau số có giá trị ~X~ của dãy ~B~;
Loại 2: Cho hai số ~Y~ và ~H~, yêu cầu xóa đi ~H~ số ngay sau số có giá trị ~Y~ của dãy ~B~;
Loại 3: Cho hai số ~L~ và ~R~, yêu cầu tính tổng của các số từ vị trí ~L~ đến vị trí ~R~ của dãy ~B~. Vị trí các phần tử trong dãy ~B~ được đánh số từ 1.
Yêu cầu: Hãy thực hiện các yêu cầu đó theo đúng thứ tự mà thầy Lê đưa ra.
Input
Vào từ file văn bản TSEQ.INP:
Dòng đầu chứa một số nguyên ~Q~ là số lượng yêu cầu thầy Lê cần thực hiện ~(1 \leq Q \leq 5 \times 10^5)~.
Mỗi dòng trong số ~Q~ dòng tiếp theo chứa ba số nguyên mô tả một trong ba loại yêu cầu theo định dạng sau:
Loại 1: 1 X K mô tả yêu cầu loại 1 ~(0 \leq X \leq 10^9; 1 \leq K \leq 10^9)~. Dữ liệu bảo đảm tổng ~K~ của tất cả các yêu cầu loại 1 không quá ~10^9~ và giá trị ~X~ hiện đang có trong dãy ~B~;
Loại 2: 2 Y H mô tả yêu cầu loại 2 ~(0 \leq Y \leq 10^9; 1 \leq H \leq 10^9)~. Dữ liệu bảo đảm có ít nhất ~H~ số sau giá trị ~Y~ và giá trị ~Y~ hiện đang có trong dãy ~B~;
Loại 3: 3 L R mô tả yêu cầu loại 3 ~(1 \leq L \leq R \leq |B|)~, với ~|B|~ là số lượng phần tử hiện tại của dãy ~B~.
Các số trên cùng một dòng cách nhau bởi dấu cách.
Output
Ghi ra file văn bản TSEQ.OUT:
- Với mỗi yêu cầu loại 3, ghi ra trên một dòng một số nguyên là đáp án tính được.
Scoring
| Subtask | Điểm | Điều kiện |
|---|---|---|
| ~1~ | ~15~ | ~Q, K \leq 500~ |
| ~2~ | ~15~ | ~Q \leq 5000~ |
| ~3~ | ~20~ | Không có yêu cầu loại ~2~; Các yêu cầu loại ~1~ xuất hiện trước tất cả các yêu cầu loại ~3~. |
| ~4~ | ~25~ | Không có yêu cầu loại ~2~. |
| ~5~ | ~25~ | Không có ràng buộc nào thêm. |
Sample Input 1
6
1 0 3
1 1 2
3 3 5
2 4 2
1 4 4
3 2 7
Sample Output 1
11
35
Notes
| Yêu cầu | Dãy B | Giải thích |
|---|---|---|
| Ban đầu | [0] | |
| 1 | [0, 1, 2, 3] | |
| 2 | [0, 1, 4, 5, 2, 3] | |
| 3 | [0, 1, 4, 5, 2, 3] | Các số từ vị trí 3 đến 5 là [4, 5, 2] có tổng là 11 |
| 4 | [0, 1, 4, 3] | |
| 5 | [0, 1, 4, 6, 7, 8, 9, 3] | |
| 6 | [0, 1, 4, 6, 7, 8, 9, 3] | Các số từ vị trí 2 đến 7 là [1, 4, 6, 7, 8, 9] có tổng là 35 |
Điểm: 6
Ngày nay, lĩnh vực an ninh mạng đang dần trở thành một lĩnh vực thiết yếu trong việc bảo mật an toàn thông tin trên toàn thế giới. Tuấn là một kỹ sư an ninh mạng và rất đam mê khám phá các bài toán về mã hóa bảo mật. Cậu đang quan tâm đến bài toán mã hóa một dãy số ~S=(S_1, S_2, \ldots, S_N)~ với các phần tử là số nguyên dương không quá ~K~. Cậu thử nghiệm việc mã hóa bằng cách viết ra tất cả các dãy hậu tố của dãy ~S~. Cụ thể, với mỗi ~i \in \{1, 2, \ldots, N\}~, Tuấn viết ra dãy ~A_i = (S_i, S_{i+1},\ldots,S_N)~. Sau đó, cậu sắp xếp các dãy này tăng dần theo thứ tự từ điển. Cuối cùng, cậu ghi lại độ dày của các dãy theo thứ tự đã sắp xếp, thu được dãy ~L=(L_1, L_2, \ldots, L_N)~ và gọi đây là dãy đặc trưng của ~S~.
Ví dụ, với dãy ~S~ = ~(2, 1, 4, 3, 1, 3, 4)~ thì Tuấn sẽ viết ra ~7~ dãy: ~A_1 = (2, 1, 4, 3, 1, 3, 4)~; ~A_2=(1, 4, 3, 1, 3, 4)~; ~A_3=(4, 3, 1, 3, 4)~; ~A_4=(3, 1, 3, 4)~; ~A_5=(1, 3, 4)~; ~A_6=(3, 4)~; ~A_7=(4)~. Sau khi sắp xếp tăng dần theo thứ tự từ điển, Tuấn thu được: ~(A_5, A_2, A_1, A_4, A_6, A_7, A_3)~. Cuối cùng, Tuấn ghi lại độ dài các dãy theo thứ tự đó và thu được các dãy đặc trưng của ~S~ là ~L =~ (~3, 6, 7, 4, 2, 1, 5~).
Nhắc lại, dãy ~(X_1, X_2, \ldots, X_u)~ được gọi là đi trước dãy ~(Y_1, Y_2, \ldots, Y_v)~ theo thứ tự từ điển nếu một trong hai điều kiện sau thỏa mãn:
Tồn tại ~i \in \{1, 2, \ldots, min(u, v)\}~ sao cho ~X_1 = Y_1, X_2 = Y_2, \ldots, X_{i - 1} = Y_{i - 1}~ và ~X_i < Y_i~;
~X_1 = Y_1, X_2 = Y_2, \ldots, X_u = Y_u~ và ~u < v~.
Bây giờ Tuấn muốn biết khả năng giải mã ngược lại ra dãy ~S~ nếu chỉ biết số ~K,~ dãy ~L~ và phương pháp xây dựng dãy ~L~. Tuấn nhận ra rằng có thể tồn tại nhiều dãy ~S~ có các phần tử là các số nguyên dương không quá ~K~ mà sau khi thực hiện phương pháp mã hóa như trên có thể cho ra cùng một dãy đặc trưng ~L~.
Tiếp tục quá trình thử nghiệm, Tuấn thực hiện ~Q~ phép biến đổi liên tiếp trên dãy ~L~. Với mỗi phép biến đổi, cậu sẽ chọn hai phần tử của dãy ~L~ hiện tại và đổi giá trị cho nhau, sau đó đếm số dãy ~S~ thỏa mãn dãy đặc trưng ~L~ vừa được biến đổi. Sau mỗi phép biến đổi, dãy ~L~ được cập nhật.
Yêu cầu: Cho biết ~N, K~, dãy ~L~ và các phép biến đổi của Tuấn. Trước lần biến đổi đầu tiên và sau mỗi lần biến đổi của Tuấn trên dãy ~L~, hãy tính số lượng dãy ~S~ có ~N~ phần tử, các phần tử là các số nguyên dương không quá ~K~, sao cho dãy đặc trưng của ~S~ là dãy ~L~.
Input
Vào từ file văn bản ENCODE.INP:
Dòng đầu tiên chứa ba số nguyên ~N, K, Q~ (~1 \leq N, K \leq 5 \times 10^5~, ~0 \leq Q \leq 5 \times 10^5~).
Dòng thứ hai chứa ~N~ số nguyên dương ~L_1, L_2, \ldots, L_N~. Dữ liệu đảm bảo dãy ~L=(L_1, L_2, \ldots, L_N)~ là một hoán vị của ~N~ số tự nhiên ~1, 2, \ldots, N~.
Mỗi dòng trong số ~Q~ dòng tiếp theo chứa hai số nguyên dương khác nhau ~i, j~ ~(1 \leq i, j \leq N)~ mô tả một phép biến đổi của Tuấn với ý nghĩa là đổi giá trị của ~L_i~ và ~L_j~ cho nhau.
Các số trên cùng một dòng cách nhau bởi dấu cách.
Output
In ra file văn bản ENCODE.OUT:
- Gồm ~Q + 1~ dòng, mỗi dòng là phần dư trong phép chia cho ~1\,000\,000\,007~ của số lượng dãy ~S~ tính được cho dãy ~L~ ban đầu và cho dãy ~L~ sau mỗi phép biến đổi theo thứ tự đầu vào.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~10\%~ | ~N, K, Q \leq 8.~ |
| 2 | ~10\%~ | ~N, Q \leq 8.~ |
| 3 | ~24\%~ | ~Q=0~ và ~L~ là dãy tăng dần hoặc giảm dần. |
| 4 | ~28\%~ | ~N, K, Q \leq 1000.~ |
| 5 | ~28\%~ | Không có ràng buộc nào thêm. |
Sample Input 1
3 3 2
3 1 2
2 3
1 2
Sample Output 1
4
4
1
Notes
Các dãy ~S~ có dãy đặc trưng ~L=(3, 1, 2)~ là: ~(1, 2, 2)~; ~(1, 3, 3)~;, ~(2, 3, 3)~; ~(1, 3, 2)~.
Các dãy ~S~ có dãy đặc trưng ~L=(3, 2, 1)~ là: ~(1, 1, 2)~; ~(1, 1, 3)~; ~(2, 2, 3)~; ~(1, 2, 3)~.
Các dãy ~S~ có dãy đặc trưng ~L=(2, 3, 1)~ là: ~(2, 1, 3)~.