VOI 25 Bài 4 - Vòng tròn
Xem dạng PDFMột trường THPT chuyên đang tổ chức trò chơi tập thể cho ~M~ học sinh lớp chuyên Toán đánh số từ 1 đến ~M~ và ~L~ học sinh lớp chuyên Văn đánh số từ ~1~ đến ~L~. Trên sân, có ~N~ vị trí cách đều nhau đã được đánh dấu sẵn, các vị trí được đánh số từ ~1~ đến ~N~ tạo thành một vòng tròn:
Vị trí thứ ~1~ kề với vị trí thứ ~2~ và thứ ~N~;
Vị trí thứ ~i~ ~(2 \le i \le N-1)~ kề với vị trí thứ ~i-1~ và thứ ~i+1~;
Vị trí thứ ~N~ kề với vị trí thứ ~N-1~ và vị trí ~1~.
Ban đầu ~M+L~ học sinh đứng ở các vị trí sao cho không có ~2~ học sinh nào đứng cùng một vị trí. Học sinh thứ ~u~ của lớp chuyên Toán đứng ở vị trí ~P_u (1 \le u \le M)~, học sinh thứ ~v~ của lớp chuyên Văn đứng ở vị trí ~Q_v (1 \le v \le L)~. Mỗi bước, học sinh có thể di chuyển sang một trong ~2~ vị trí kề với vị trí đang đứng. Lưu ý, trong quá trình di chuyển, một vị trí có thể có nhiều hơn một học sinh. Các thầy cô muốn xác định vị trí tập trung của từng bạn sao cho:
Vị trí tập trung của ~M~ học sinh lớp chuyên Toán là ~M~ vị trí liên tiếp trên vòng tròn;
Vị trí tập trung của ~L~ học sinh lớp chuyên Văn là ~L~ vị trí liên tiếp trên vòng tròn;
Không có ~2~ học sinh nào đứng cùng một vị trí.
Yêu cầu: Hãy giúp các thầy cô xác định vị trí tập trung của các học sinh sao cho tổng số bước phải di chuyển của tất cả học sinh là nhỏ nhất.
Input
Vào từ file văn bản CYCLE.INP: Dòng đầu chứa một số nguyên ~T~ là số lượng trường hợp test ~(1 \le T \le 10^5)~. Tiếp theo ~T~ nhóm dòng, mỗi nhóm dòng mô tả một trường hợp test như sau:
Dòng thứ nhất chứa ~3~ số nguyên dương ~N, M~ và ~L (2 \le M + L \le N \le 10^5)~.
Dòng thứ hai chứa ~M~ số nguyên dương ~P_1, P_2, \ldots, P_M (1 \le P_1, P_2, \ldots, P_M \le N)~.
Dòng thứ ba chứa ~L~ số nguyên dương ~Q_1, Q_2, \ldots, Q_L (1 \le Q_1, Q_2, \ldots, Q_L \le N)~.
Dữ liệu đảm bảo tổng các số ~N~ trong một file dữ liệu vào không vượt quá ~2 \times 10^5~. Các số trên cùng một dòng cách nhau bởi dấu cách.
Output
Ghi ra file văn bản CYCLE.OUT:
- Gồm ~T~ dòng, mỗi dòng chứa một số nguyên duy nhất là tổng số bước di chuyển nhỏ nhất của tất cả học sinh tương ứng với trường hợp test trong dữ liệu vào.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~10\%~ | ~N \le 10; T \le 10.~ |
| 2 | ~15\%~ | ~N \le 500; 1 \le P_1, P_2, \ldots, P_M \lt \frac{N}{2}; 1 \le Q_1, Q_2, \ldots, Q_L \lt \frac{N}{2}; T \le 10.~ |
| 3 | ~15\%~ | ~N \le 5000; 1 \le P_1, P_2, \ldots, P_M \lt \frac{N}{2}; 1 \le Q_1, Q_2, \ldots, Q_L \lt \frac{N}{2}; T \le 10.~ |
| 4 | ~20\%~ | ~N \le 5000; T \le 10.~ |
| 5 | ~20\%~ | ~1 \le P_1, P_2, \ldots, P_M \lt \frac{N}{2}; 1 \le Q_1, Q_2, \ldots, Q_L \lt \frac{N}{2}; T \le 10.~ |
| 6 | ~20\%~ | Không có ràng buộc nào thêm. |
Sample Input 1
1
12 6 4
1 3 5 7 9 11
2 12 8 4
Sample Output 1
15
Notes
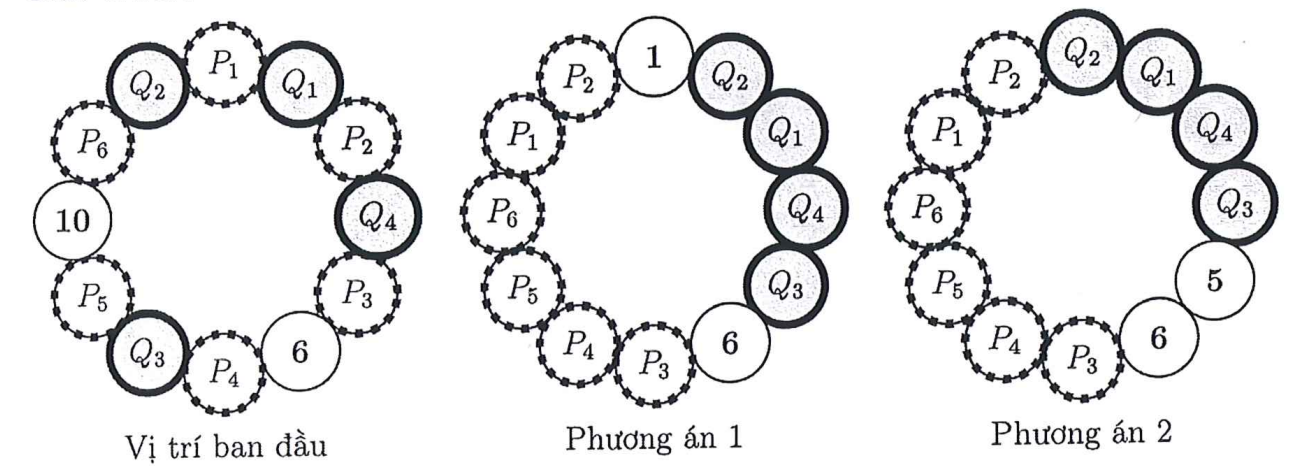
Trong phương án ~1~, số bước di chuyển của các học sinh chuyên Văn lần lượt là: ~1,2,3,0~; số bước di chuyển của các học sinh chuyên Toán lần lượt là: ~2,3,2,1,0,1~.
Trong phương án ~2~, số bước di chuyển của các học sinh chuyên Văn lần lượt là: ~0,1,4,1~; số bước di chuyển của các học sinh chuyên Toán lần lượt là: ~2,3,2,1,0,1~.
Cả hai phương án đều tối ưu và đều có tổng số bước là ~15~.

Bình luận
cho mình hỏi là bài này vị trí có được sắp xếp sẵn không
Trong đề bài, phần input không có đề cập tới việc ~P_i~ hay ~Q_i~ được sắp xếp tăng dần / giảm dần. Nên ông cứ mặc định là không có nhé.
Bình luận này đã bị ẩn vì có quá nhiều phản ứng tiêu cực. Nhấn để xem.