[Mirror] VNOI Cup 2025 - Final
Điểm: 500
Sau một ngày dài vui chơi với những fan hâm mộ cua của mình, Saba chuẩn bị trở về ngọn hải đăng trên một chiếc thuyền giấy nhỏ băng qua biển. Muốn tiễn Saba lần cuối trước khi trời tối, những chú cua quyết định xếp hàng dọc theo lộ trình chèo thuyền của cô để tạm biệt. Vì số lượng fan của Saba đã vượt quá một triệu, những chú cua cần phải đứng đủ thưa để Saba có thể chèo thuyền về nhà an toàn.
Lộ trình chèo thuyền được mô hình dưới dạng lưới với ~k~ hàng và ~2^{60}~ cột. Các hàng được đánh số từ ~0~ đến ~k - 1~ từ trên xuống dưới, và các cột được đánh số từ ~0~ đến ~2^{60} - 1~, bắt đầu từ bờ biển. Bờ biển nằm trước cột ~0~, và nhà của Saba nằm ngay sau cột ~2^{60} - 1~. Nắm được điều này, những chú cua đã phối hợp để xếp hàng như sau:
Các chú cua chọn ra hai số ~l~ và ~r~, sao cho ~0 \le l \le r < 2^{60}~;
Đối với mỗi cột ~i~ từ ~l~ đến ~r~, một chú cua sẽ đứng ở hàng thứ ~j~ nếu và chỉ nếu bit thứ ~j~ từ bên phải của ~i~ là ~0~ (nói cách khác, ~\left\lfloor \frac{i}{2^j} \right\rfloor~ chẵn);
Không có chú cua nào đứng ở bất kỳ ô nào khác của lưới.
Saba phải điều hướng qua các fan của mình để về nhà như sau.
Bắt đầu từ bờ biển, Saba có thể chọn một ô trống ở cột thứ ~0~ để đặt chiếc thuyền giấy của mình.
Saba có thể về đến nhà nếu cô ấy di chuyển được đến một ô trống ở cột thứ ~(2^{60} - 1)~.
Chiếc thuyền có thể di chuyển từ một ô sang ô khác nếu hai ô đó có cạnh chung.
Chiếc thuyền không được rời khỏi lưới.
Và vì chiếc thuyền cực kỳ mong manh, nó sẽ hỏng nếu nó đi vào cùng một ô chứa một chú cua.
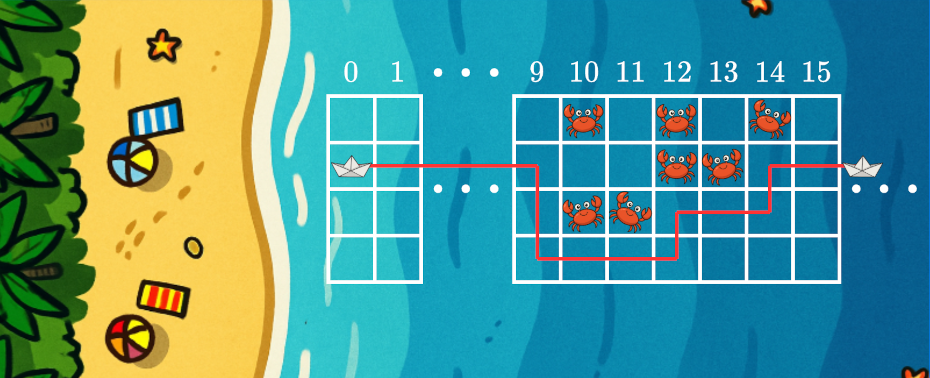
Minh họa cho test case đầu tiên: ~l = 10~, ~r = 14~, ~k = 4~. Saba có thể trở về nhà an toàn.
Thấy được sự tận tâm của những người hâm mộ, Saba rất cảm động! Tuy nhiên, cô nổi tiếng là kém toán, vì vậy cô không chắc liệu mình có thể về nhà an toàn hay không. Giúp Saba xác định xem có một lối đi an toàn về nhà hay không, dựa trên cách sắp xếp của những chú cua.
Input
Dòng đầu tiên chứa một số nguyên dương ~t~ (~1 \leq t \leq 10\,000~) – số lượng testcase.
Dòng đầu tiên và duy nhất của mỗi testcase chứa 3 số ~l~, ~r~, ~k~ (~0 \leq l \leq r < 2^{60}~, ~1 \leq k \leq 60~) – khoảng cột mà những chú cua sẽ đứng, và số lượng hàng.
Output
Với mỗi testcase, in ra ~\mathtt{YES}~ nếu có một lối đi để Saba có thể an toàn về nhà, hoặc ~\mathtt{NO}~ nếu không.
Scoring
Tổng điểm cho bài này là ~500~.
Sample Input 1
6
10 14 4
52 54 7
100 200 60
999999999999999999 1000000000000000000 1
6 6 1
15 29 3
Sample Output 1
YES
YES
NO
NO
NO
NO
Notes
Test case đầu tiên đã được giải thích qua hình minh họa ở phần đề bài.
Trong test case thứ hai: ~l = 52~, ~r = 54~, ~k = 7~. Dưới đây là minh họa cho vị trí đứng của các chú cua và cách Saba di chuyển qua:
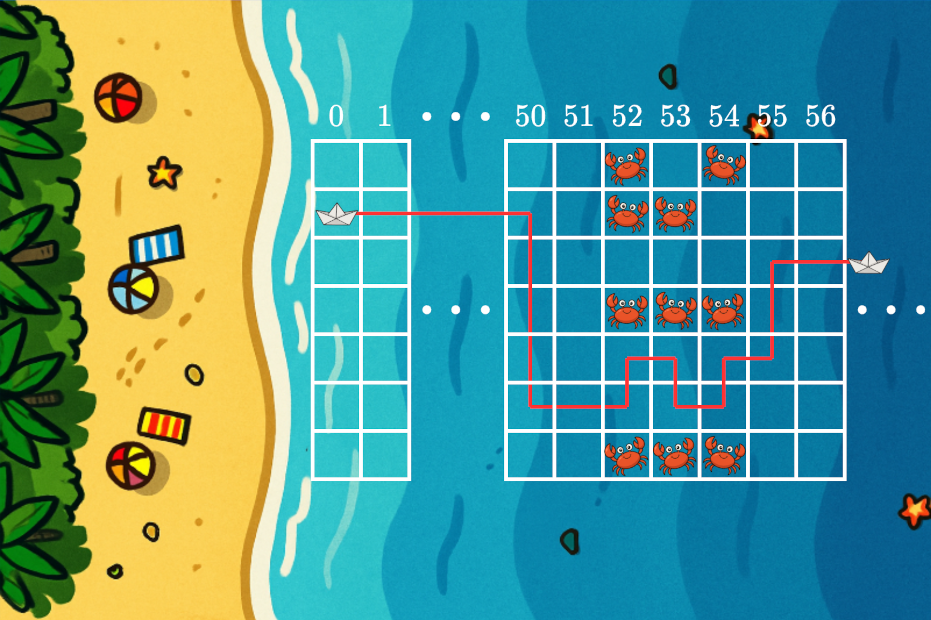
Trong các test case còn lại, tất cả mọi con đường về nhà đều phải đi qua ít nhất một chú cua, do đó không có cách để Saba có thể di chuyển về nhà một cách an toàn.
Là một họa sĩ tài ba, Văn được mời làm giám khảo cho một kỳ thi hội họa do VNOI tổ chức. Mỗi thí sinh tham gia sẽ phải tự mình vẽ lên một bức họa là một bảng hình lưới có kích thước ~n \times m~, với hàng được đánh số từ ~1~ đến ~n~ theo thứ tự từ trên xuống dưới, và cột được đánh số từ ~1~ đến ~m~ từ trái qua phải. Ô nằm ở hàng ~i~ và cột ~j~ trên lưới mang một giá trị số nguyên ~c_{i,j}~, biểu thị chỉ số màu của ô đó trong bức tranh. Văn sẽ là người thẩm định các bài dự thi và quyết định kết quả chung cuộc.
Tuy nhiên, trong thời đại AI phát triển mạnh mẽ, rất có khả năng một số thí sinh đã lợi dụng AI để làm giả bài thi của mình. Qua quá trình điều tra, Văn phát hiện ra cách AI được sử dụng để sinh ra bức tranh như sau:
AI xuất phát từ một bức vẽ trống, với mọi ô có màu ~c_{i,j} = 0~.
AI sử dụng một trong hai thao tác sau (không hoặc nhiều lần) để tô màu cho bức tranh:
Chọn một hàng bất kỳ (~1 \leq i \leq n~) và màu ~c~, tô các ô nằm trên hàng đó bằng màu ~c~.
Chọn một cột bất kỳ (~1 \leq j \leq m~) và màu ~c~, tô các ô nằm trên cột đó bằng màu ~c~.
Văn biết bạn là một kỹ sư tài năng, do đó Văn nhờ bạn kiểm tra xem bức tranh của thí sinh có thể là do AI tạo ra hay không, và nếu có thể, hãy đưa ra một trình tự bất kỳ các thao tác vẽ thỏa mãn để làm bằng chứng.
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên của bộ dữ liệu chứa số nguyên dương ~t~ (~1 \leq t \leq 100~) – số lượng testcase. Mô tả của mỗi test case như sau:
Dòng đầu tiên chứa hai số nguyên dương ~n, m~ (~1 \leq n, m \leq 1500~) – số lượng hàng và cột của lưới bảng vẽ.
Dòng thứ ~i~ trong ~n~ dòng tiếp theo, mỗi dòng chứa ~m~ số nguyên dương ~c_{i,1}, c_{i,2}, \ldots, c_{i,m}~ (~1 \le c_{i,j} \le n \cdot m~) – chỉ số màu của các ô nằm trên hàng thứ ~i~.
Đảm bảo rằng:
tổng của ~n~ qua các testcase không vượt quá ~1500~,
tổng của ~m~ qua các testcase không vượt quá ~1500~.
Output
Với mỗi test case, nếu chắc chắn rằng bài làm không phải do AI tạo ra, hãy in ra ~\mathtt{NO}~. Ngược lại,
Dòng đầu tiên, hãy in ra ~\mathtt{YES}~.
Dòng tiếp theo, hãy in ra một số nguyên ~k~ (~1 \leq k \leq 5000~) là số phép vẽ cần có cho bảng vẽ. Không yêu cầu cách vẽ phải tối ưu.
Mỗi dòng ~i~ trong ~k~ dòng tiếp theo hãy in ra ba số nguyên ~t, j, c~ (~t = 0~, ~1 \le j \le n~ hoặc ~t = 1~, ~1 \le j \le m~; ~1 \le c \le n \cdot m~) – mô tả thao tác vẽ thứ ~i~.
~t = 0~ với thao tác tô hàng, ~t = 1~ với thao tác tô cột,
~i~ là vị trí hàng hoặc cột của thao tác,
~c~ là chỉ số màu vẽ.
Nếu như tồn tại cách vẽ, có thể chứng minh rằng rằng cần không quá ~5000~ thao tác với giới hạn đã cho.
Nếu như có nhiều cách vẽ thỏa mãn, hãy in ra cách vẽ bất kỳ.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~500~ | ~\sum n, \sum m \leq 200~ |
| 2 | ~750~ | Không có ràng buộc gì thêm |
| Tổng | ~1250~ |
Sample Input 1
2
3 3
1 1 3
1 1 3
2 2 2
2 2
1 2
3 4
Sample Output 1
YES
4
0 1 1
0 2 1
1 3 3
0 3 2
NO
Sample Input 2
2
3 4
1 1 1 1
1 1 1 1
1 2 2 1
5 20
8 8 8 8 1 8 1 1 1 1 1 8 1 1 8 1 8 8 8 8
8 1 1 1 1 8 1 1 1 1 1 8 1 1 8 1 8 1 1 1
8 1 8 8 1 8 1 1 1 1 1 8 8 8 8 1 8 8 8 8
8 1 1 8 1 8 1 1 1 1 1 8 1 1 8 1 8 1 1 1
8 8 8 8 1 8 8 8 8 1 1 8 1 1 8 1 8 1 1 1
Sample Output 2
YES
6
1 4 1
1 3 2
1 2 2
1 1 1
0 2 1
0 1 1
NO
Notes
Dưới đây là hình minh họa cho test case thứ nhất của ví dụ đầu tiên.
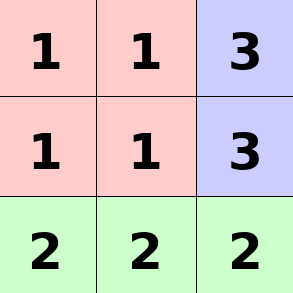
Để vẽ được hình này ta cần ~4~ đường vẽ theo thứ tự như sau:
Kẻ màu ~1~ (màu đỏ trong hình) ở cột 1, 2
Kẻ màu ~3~ (màu xanh dương trong hình) ở cột 3
Kẻ màu ~2~ (màu xanh lá trong hình) ở hàng 3.
Dưới đây là minh họa cho test case thứ hai của ví dụ đầu tiên. Có thể thấy không có cách vẽ nào để tạo ra được bảng như trên. Đây là một bài làm hợp lệ.
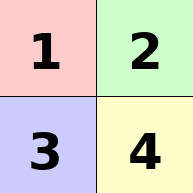
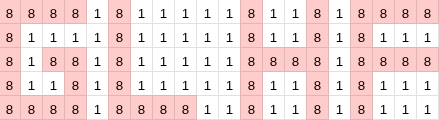
Dưới đây là hình minh họa cho test case thứ hai của ví dụ thứ hai. Good luck!
Điểm: 1500
Chắc hẳn bạn nào học tin cũng biết đến thuật toán sàng số nguyên tố sau đây khi được học đến phần số học. Dưới đây là mã giả của thuật toán sàng:
function sieve(n, values):
primes := []
is_prime := array[2..n], initialized to true
for v in values do:
if not is_prime[v] then:
continue
end if
append v to primes
for i := 2 to ⌊n / v⌋ do:
is_prime[i * v] := false
end for
end for
return primes
end function
// ...
primes = sieve(n, [2, 3, ..., n])
Bí quyết để ghi nhớ thuật toán này, cũng như để chứng minh được tính đúng đắn, là khi duyệt đến một giá trị ~v~ bất kỳ, ta đánh dấu tất cả các bội của ~v~ là hợp số.
Sau khi giảng cho bạn thuật toán này, thầy giáo đã rất kinh ngạc khi thấy bạn đã hiểu và có khả năng áp dụng nó rất nhanh. Thầy giáo đành phải ra thêm bài tập bổ sung xoay quanh thuật toán này. Mỗi bài tập của thầy giáo gồm số nguyên ~n~ và mảng số nguyên ~a~ là hoán vị~^*~ của ~n - 1~ số nguyên ~[2, 3, \ldots, n]~. Thầy giáo muốn bạn thay đổi mảng ~a~, sao cho khi thực hiện thuật toán ~\mathtt{sieve}(n, a)~, kết quả thu được là một danh sách chỉ bao gồm số nguyên tố.
Để làm điều này, thầy giáo cho phép bạn thực hiện thao tác sau (không hoặc nhiều lần):
- Chọn hai phần tử kề nhau trong ~a~ sao cho có chính xác một phần tử được chọn là số nguyên tố và phần tử còn lại là hợp số, rồi hoán đổi vị trí của hai phần tử này.
Ví dụ, với ~a = [\underline{2}, 4, \underline{5}, \underline{3}, 8, 6, \underline{7}]~, được phép đổi chỗ cặp phần tử ~(2, 4)~, ~(4, 5)~, ~(3, 8)~ hoặc ~(6, 7)~. Các cặp phần tử sau không được phép đổi chỗ:
~(4, 3)~, do chúng không kề nhau,
~(5, 3)~, do chúng cùng là số nguyên tố,
~(8, 6)~, do chúng cùng là hợp số.
Thầy giáo muốn bạn giải đáp bài tập càng nhanh càng tốt. Do đó với mỗi câu đố, bạn muốn tìm xem cần thực hiện ít nhất bao nhiêu thao tác để giải đáp bài tập đó. Có thể chứng minh được rằng với mọi mảng ~a~ hợp lệ, tồn tại mỗi dãy các thao tác đổi chỗ sao cho ~\mathtt{sieve}(n, a)~ là một danh sách chỉ bao gồm số nguyên tố.
————————————————–
~^*~ Một hoán vị của một dãy là một dãy khác có cùng tập hợp các phần tử (bao gồm cả các phần tử trùng lặp, nếu có), nhưng có thể được sắp xếp theo bất kỳ thứ tự nào. Ví dụ, ~[1, 2, 2, 3]~, ~[2, 3, 1, 2]~, và ~[2, 2, 1, 3]~ là một số hoán vị của ~[3, 2, 1, 2]~, nhưng ~[2, 4, 3, 1]~, ~[2, 1, 2]~, và ~[1, 1, 2, 3]~ thì không.
Input
Dòng đầu tiên gồm số nguyên ~t~ (~1 \le t \le 10\,000~) – số lượng bài tập thầy giáo ra cho bạn. Mô tả của mỗi bài tập như sau.
Dòng đầu tiên gồm số nguyên ~n~ (~2 \le n \le 10^6~).
Dòng thứ hai gồm ~n - 1~ số nguyên ~a_1, a_2, \ldots, a_{n - 1}~ (~2 \le a_i \le n~, ~a_i \ne a_j~ với mọi ~i \ne j~).
Đảm bảo rằng tổng ~n~ qua tất cả các bài tập không quá ~10^6~.
Output
Với mỗi bài tập, in ra số thao tác hoán đổi phần tử mảng ~a~ ít nhất, sao cho ~\mathtt{sieve}(n, a)~ là một danh sách chỉ bao gồm số nguyên tố.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~750~ | ~\sum{n} \leq 5000~ |
| 2 | ~750~ | Không có ràng buộc gì thêm |
| Tổng | ~1500~ |
Sample Input 1
4
3
3 2
4
4 3 2
8
7 6 2 3 4 5 8
9
4 6 9 2 8 5 7 3
Sample Output 1
0
2
1
9
Notes
Trong bài tập đầu tiên, ta có ~a = [3, 2]~. Ta không cần sử dụng thêm thao tác gì vì khi đó kết quả khi thực hiện ~\mathtt{sieve}(3, [3, 2])~ là ~[3, 2]~.
Trong bài tập thứ hai, ta có ~a = [4, 3, 2]~. Ta có thể sử dụng 2 thao tác để biến đổi ~a~ thành ~[3, 2, 4]~. Khi đó ~\mathtt{sieve}(3, [3, 2, 4]) = [3, 2]~.
Trong bài tập thứ ba, ta có thể đảo chỗ vị trí của phần tử ~6~ và ~2~.
Điểm: 2250
Bạn được cho đồ thị có hướng liên thông yếu~^*~ gồm ~n~ đỉnh và ~m~ cạnh có dạng ~u_i \to v_i~ với ~1 \le i \le m~, một xâu nhị phân ~s~ có độ dài là ~m~, và một hoán vị ~p~ của các giá trị từ ~1~ tới ~n~. Bạn được thực hiện thao tác sau không hay nhiều lần:
- Chọn một chỉ số ~i~ từ ~1~ tới ~m~. Hoán đổi giá trị của ~p_{u_i}~ và ~p_{v_i}~, và đồng thời đảo chiều cạnh thứ ~i~ của đồ thị (nếu cạnh này đang là ~u_i \to v_i~ thì sẽ biến thành ~v_i \to u_i~, và ngược lại).
Bạn muốn thực hiện các thao tác trên cho đến khi cả hai điều kiện sau được thoả mãn.
Hoán vị ~p~ thoả mãn ~p_i = i~ với mọi ~1 \le i \le n~.
Với mọi cạnh ~u_i \to v_i~ (~1 \le i \le m~) ở đồ thị ban đầu, nếu ~s_i = \mathtt{0}~ thì cạnh này không bị đảo chiều, ngược lại thì cạnh này bị đảo chiều.
Bạn cần xác định xem có tồn tại dãy thao tác nào để thoả mãn hai điều kiện trên hay không. Nếu có, hãy tìm một dãy thao tác như vậy với tối đa ~4n^2~ thao tác.
————————————
~^*~ Một đồ thị có hướng được gọi là liên thông yếu khi và chỉ khi nếu thay thế toàn bộ cạnh có hướng ~u \to v~ của đồ thị thành cạnh vô hướng ~(u, v)~, thì đồ thị vô hướng thu được là liên thông.
Input
Dòng đầu tiên chứa số nguyên ~t~ (~1 \le t \le 10\,000~) – số lượng test case. Mô tả của mỗi test case như sau.
Dòng đầu tiên chứa hai số nguyên ~n~ và ~m~ (~2 \le n \le 500, n - 1 \le m \le \frac{n(n-1)}{2}~) — số lượng đỉnh và cạnh của đồ thị. Đảm bảo rằng đồ thị đã cho liên thông yếu.
Dòng thứ hai chứa một xâu nhị phân ~s~ (~|s| = m, s_i \in \{\mathtt{0}, \mathtt{1}\}~).
Dòng thứ ba chứa ~n~ số nguyên ~p_1, p_2, \ldots, p_n~ (~1 \le p_i \le n~) là các phần tử của hoán vị mà bạn được cho.
Dòng thứ ~i~ trong ~m~ dòng tiếp theo chứa hai số nguyên ~u_i~ và ~v_i~ (~1 \le u_i, v_i \le n, u_i \neq v_i~) mô tả cạnh ~u_i \to v_i~ trên đồ thị ban đầu. Đảm bảo rằng giữa hai đỉnh bất kì trên đồ thị, tồn tại tối đa một cạnh giữa chúng.
Đảm bảo rằng tổng ~n^2~ qua tất cả các test case không quá ~250\,000~.
Output
Với mỗi test case, nếu không tồn tại dãy thao tác nào để thoả mãn cả hai điều kiện như đề bài, in ra ~\mathtt{NO}~ trên một dòng. Ngược lại
Ở dòng đầu tiên, in ra ~\mathtt{YES}~.
Ở dòng thứ hai, in ra ~k~ (~0 \le k \le 4n^2~) là số lượng thao tác cần dùng.
Ở dòng thứ ba, in ra ~k~ số nguyên ~i_1, i_2, \dots, i_k~ (~1 \le i_j \le m~) là các chỉ số mà sẽ bạn sẽ áp dụng thao tác lên. Nếu ~k = 0~, bạn có thể chọn in ra một dòng trống, hoặc bạn không in ra dòng này.
Ta có thể chứng minh rằng với giới hạn đã có, nếu tồn tại bất kì dãy thao tác nào để thoả mãn đề bài, thì cũng tồn tại dãy thao tác thoả mãn đề bài mà sử dụng tối đa ~4n^2~ thao tác.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~1000~ | ~m = n - 1~, đồng thời cạnh thứ ~i~ của đồ thị nối giữa đỉnh ~i~ và ~i + 1~ với mọi ~1 \le i \le m~ |
| 2 | ~1250~ | Không có ràng buộc gì thêm |
| Tổng | ~2250~ |
Sample Input 1
4
5 7
0100101
2 4 1 3 5
5 1
2 4
2 3
1 3
4 3
1 4
4 5
5 7
0100101
3 2 1 5 4
5 1
2 4
2 3
1 3
4 3
1 4
4 5
4 6
000000
1 2 3 4
1 2
1 3
1 4
2 3
2 4
3 4
3 2
11
1 2 3
1 2
2 3
Sample Output 1
YES
5
1 5 7 1 2
NO
YES
0
YES
6
1 2 1 2 1 2
Notes
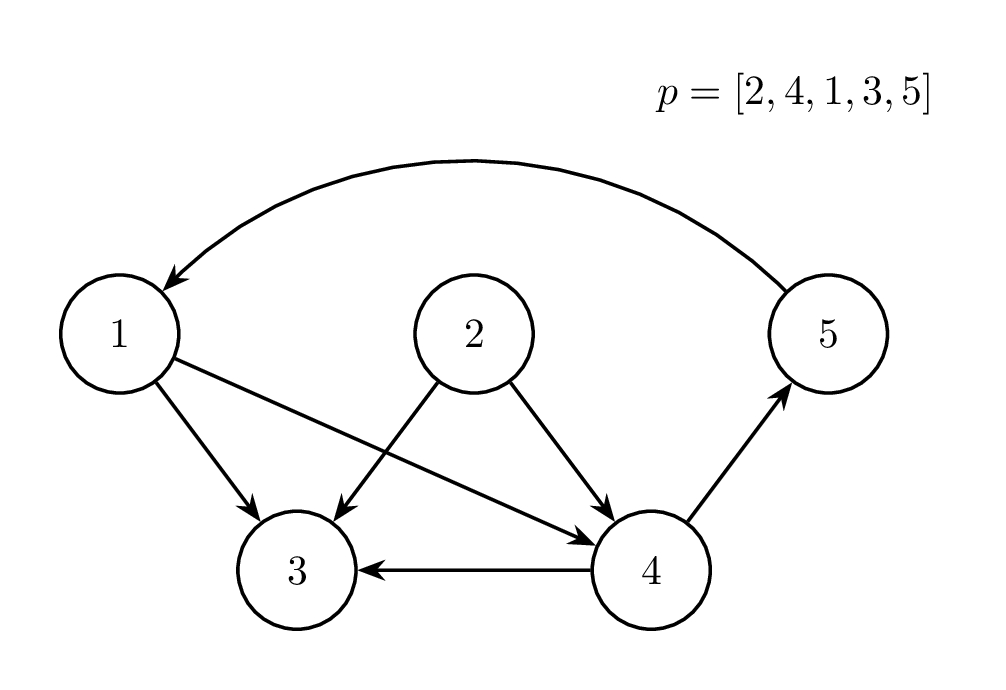
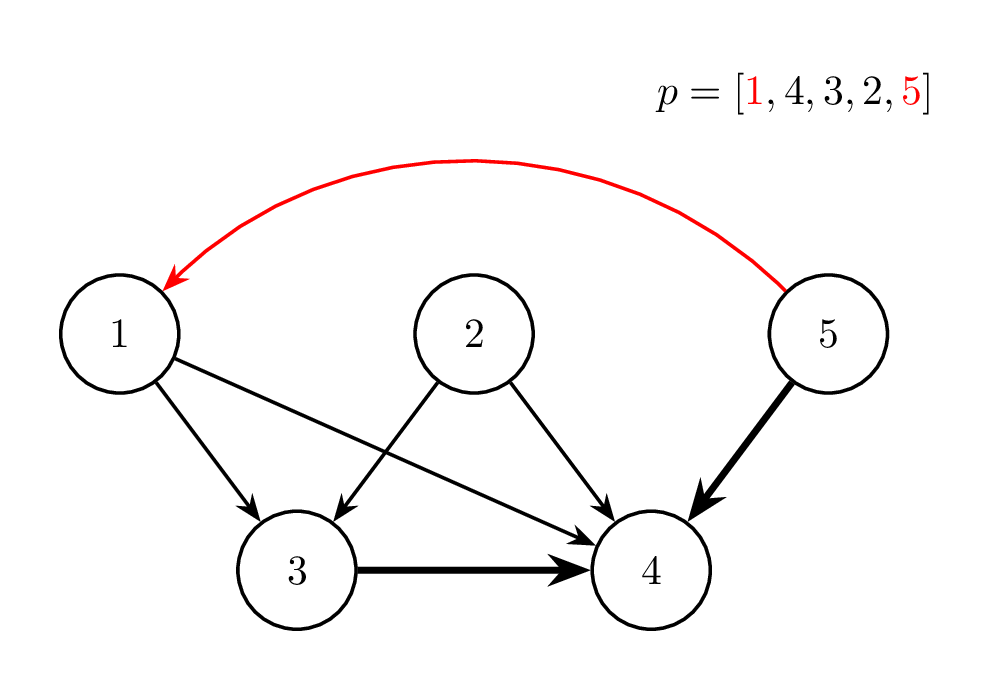
Sáu hình dưới đây minh hoạ cho các phép biến đổi trong test case thứ nhất. Ở mỗi hình, màu đỏ chỉ cạnh được đảo chiều và hai phần tử được hoán đổi ở từng phép thao tác. Ngoài ra, cạnh in đậm chỉ những cạnh đã bị đảo chiều so với đồ thị ban đầu.
Trạng thái ban đầu |
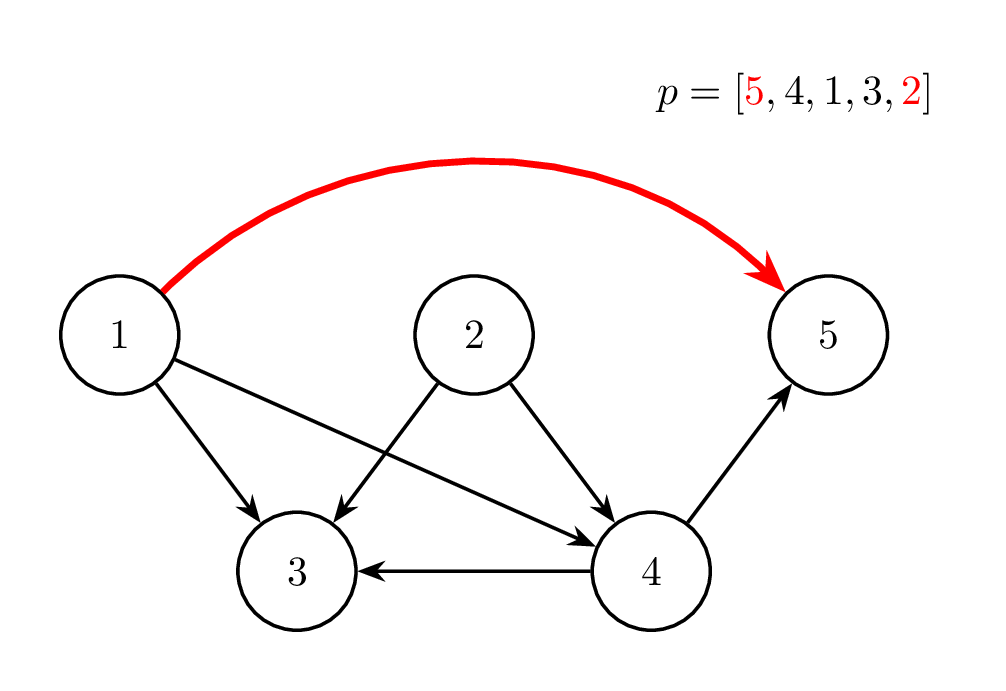
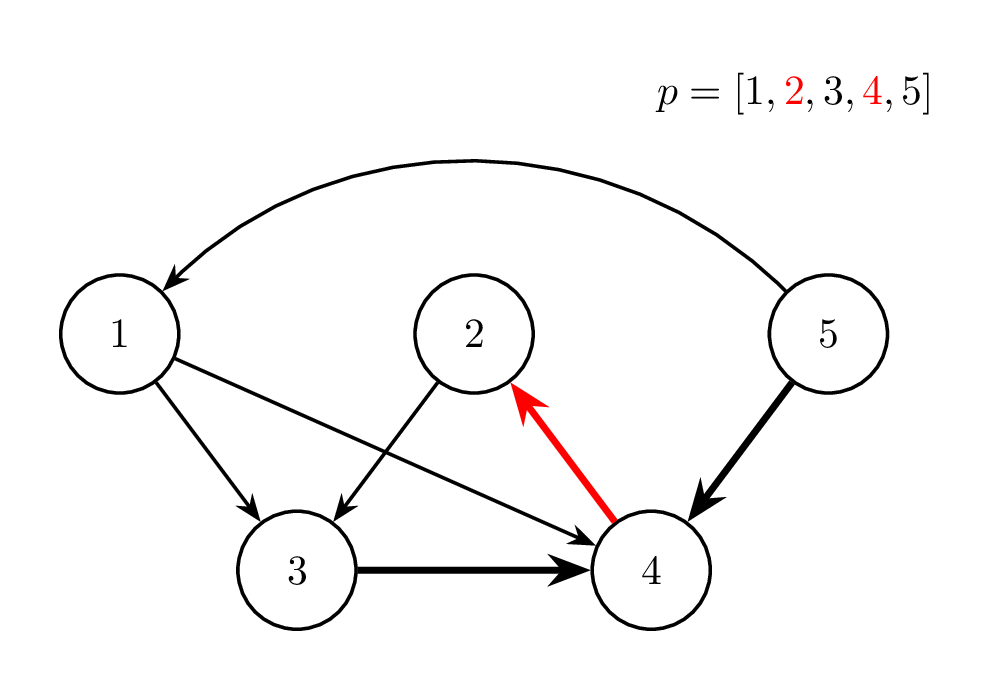
Thao tác 1: ~i = 1~ |
Thao tác 2: ~i = 5~ |
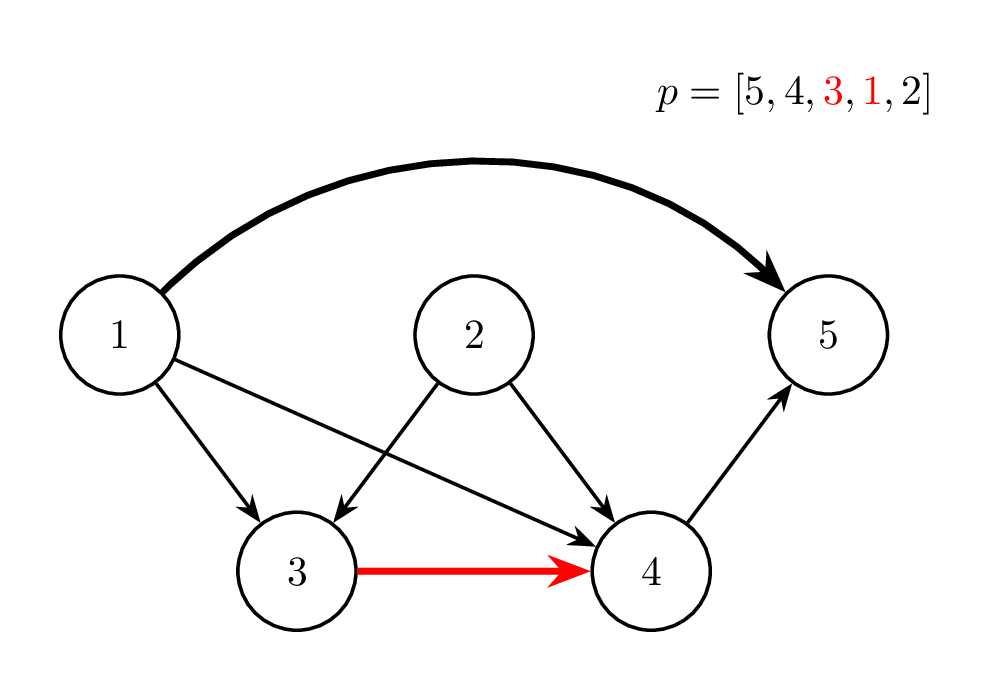
Thao tác 3: ~i = 7~ |
Thao tác 4: ~i = 1~ |
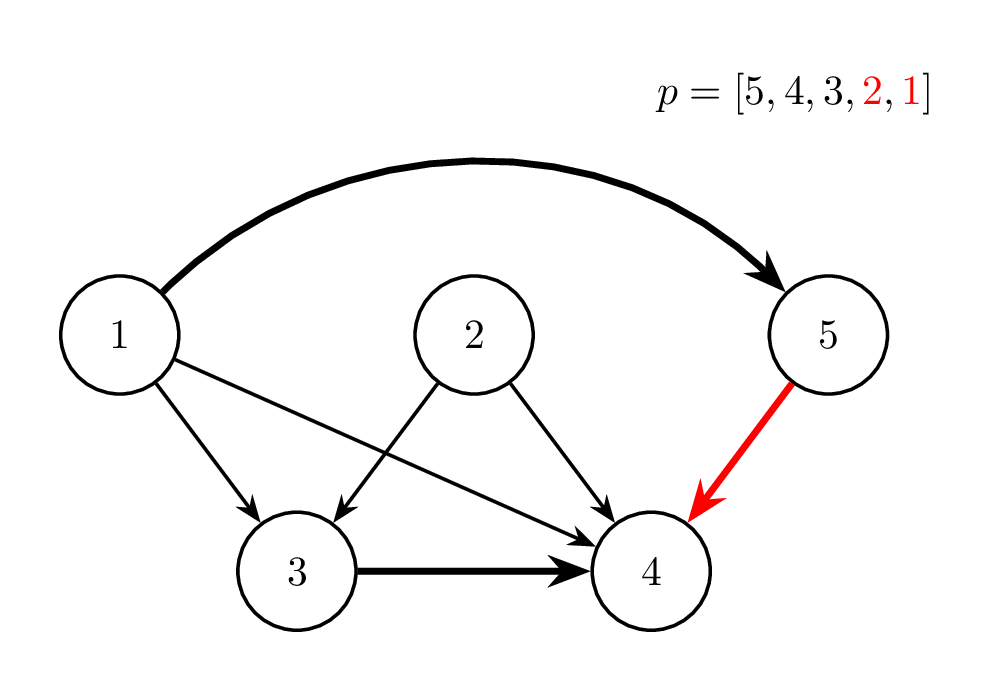
Thao tác 5: ~i = 2~ |
Điểm: 2500
Hikamura Nakaru là một kì thủ cờ tướng và streamer nổi tiếng, người từng đánh bại kỳ vương Carlos Magnussen một lần (và thua ~14~ lần). Hôm nay, Hikamura giao lưu với ~m~ thí sinh của kì thi VNOI Cup 2025. Dĩ nhiên, với khả năng của mình, Hikamura có thể dễ dàng đánh bại tất cả các thí sinh. Do vậy, để tăng sự hấp dẫn, ban tổ chức VNOI Cup đã chuẩn bị sẵn ~n~ thử thách cho Hikamura, từ những thử thách đơn giản như "chấp thời gian" hay "chấp một quân tốt" cho đến những thử thách phức tạp hơn như "quân mã không được đi lùi". Thử thách thứ ~i~ có độ khó ~a_i~. Ban tổ chức có thể chọn bao nhiêu thử thách tùy ý cho một ván cờ.
Xác suất thắng của Hikamura ở một ván cờ phụ thuộc vào độ khó của các thử thách trong ván cờ đó. Cụ thể, gọi ~S~ là tập các thử thách được chọn của ván cờ, xác suất để Hikamura thắng ván cờ này là:
$$1 - \frac{\sum_{j \in S} a_j}{\sum_{j=1}^{n} a_j}$$
Theo đó, nếu tất cả các thử thách đều được chọn thì Hikamura chắc chắn thua; ngược lại, nếu không có thử thách nào được chọn thì anh chắc chắn thắng.
Hikamura chơi ván đầu tiên với ~0~ thử thách (~S = \varnothing~). Sau mỗi ván Hikamura thắng, ban tổ chức sẽ chọn một thử thách ngẫu nhiên ~i \notin S~ và thêm vào ~S~ cho ván tiếp theo. Xác suất thử thách ~i~ được chọn là:
$$\frac{a_i}{\sum_{j \notin S} a_j}$$
Tương tự, sau mỗi ván Hikamura thua, ban tổ chức sẽ loại một thử thách ngẫu nhiên ~i \in S~ khỏi ~S~ cho ván tiếp theo. Xác suất thử thách ~i~ được bỏ là:
$$\frac{a_i}{\sum_{j \in S} a_j}$$
Hikamura sẽ chơi ~m~ ván cờ, một ván với mỗi thí sinh VNOI Cup. MofK, một thành viên ban tổ chức muốn biết giá trị kì vọng số ván thắng của Hikamura, tuy nhiên do học xác suất hơi kém nên MofK quyết định bắt các thí sinh VNOI Cup giải được bài toán này mới được chơi cờ. Hãy giúp các thí sinh nhé!
Input
Dòng đầu tiên chứa số nguyên ~t~ (~1 \leq t \leq 10\,000~) – số lượng test case. Mô tả của mỗi test case như sau:
Dòng đầu tiên chứa hai số nguyên dương ~n~, ~m~ (~1 \leq n \leq 10\,000~, ~1 \leq m \leq 10^9~) – số thử thách ban tổ chức đưa ra và số ván cờ Hikamura sẽ chơi.
Dòng thứ hai chứa ~n~ số nguyên dương ~a_1, a_2, \ldots, a_n~ (~1 \leq a_i \leq 10\,000~) – độ khó của mỗi thử thách.
Đảm bảo rằng tổng ~n~ qua tất cả các test case không vượt quá ~2 \cdot 10^5~.
Output
Với mỗi test case, in ra một số nguyên duy nhất là giá trị kì vọng số ván thắng của Hikamura, modulo ~998\,244\,353~. Cụ thể, nếu đáp án được biểu diễn dưới dạng phân số tối giản ~\frac{p}{q}~, in ra số nguyên không âm ~s < 998\,244\,353~ sao cho ~q \cdot s = p \pmod {998\,244\,353}~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~750~ | ~n \le 4~ cho mọi test case, ~t \le 100~ |
| 2 | ~1750~ | Không có giới hạn gì thêm |
| Total | ~2500~ |
Sample Input 1
4
4 1
1 4 2 3
4 2
1 4 2 3
2 3
1 1
10 420
31 41 59 26 53 58 97 93 23 84
Sample Output 1
1
99824437
2
172856962
Notes
Trong ví dụ đầu tiên, Hikaru chỉ chơi đúng một ván cờ. Do ban đầu ~S = \varnothing~, Hikaru chắc chắn sẽ chiến thắng ván cờ này, nên kì vọng số ván thắng của Hikaru là ~1~.
Trong ví dụ thứ hai, Hikaru chơi ~m = 2~ ván cờ, với ~a = [1, 4, 2, 3]~, và ~\sum_{i = 1}^4 a_i = 10~. Sau khi chiến thắng ván đấu đầu tiên, có 4 khả năng xảy ra, tương ứng với 4 cách chọn thử thách để thêm vào tập ~S~, được thể hiện qua bảng sau:
| Thử thách được thêm | Xác suất xảy ra | Xác suất Hikaru thắng |
|---|---|---|
| ~1~ | ~\frac{a_1}{\sum_{i = 1}^4 a_i} = \frac{1}{10}~ | ~\frac{a_2 + a_3 + a_4}{\sum_{i = 1}^4 a_i} = \frac{4 + 2 + 3}{10} = \frac{9}{10}~ |
| ~2~ | ~\frac{a_2}{\sum_{i = 1}^4 a_i} = \frac{4}{10}~ | ~\frac{a_1 + a_3 + a_4}{\sum_{i = 1}^4 a_i} = \frac{1 + 2 + 3}{10} = \frac{6}{10}~ |
| ~3~ | ~\frac{a_3}{\sum_{i = 1}^4 a_i} = \frac{2}{10}~ | ~\frac{a_1 + a_2 + a_4}{\sum_{i = 1}^4 a_i} = \frac{1 + 4 + 3}{10} = \frac{8}{10}~ |
| ~4~ | ~\frac{a_4}{\sum_{i = 1}^4 a_i} = \frac{3}{10}~ | ~\frac{a_1 + a_2 + a_3}{\sum_{i = 1}^4 a_i} = \frac{1 + 4 + 2}{10} = \frac{7}{10}~ |
Như vậy kì vọng số ván thắng của Hikaru là:
$$1 + \left( \frac{1}{10} \cdot \frac{9}{10} + \frac{4}{10} \cdot \frac{6}{10} + \frac{2}{10} \cdot \frac{8}{10} + \frac{3}{10} \cdot \frac{7}{10} \right) = 1 + \frac{70}{100} = \frac{17}{10}$$
Lưu ý ta cộng thêm ~1~ vì Hikaru đã thắng ván đấu đầu tiên. Ta in ra ~998\,244\,37~ do ~17 \equiv 998\,244\,37 \cdot 10 \pmod{998\,244\,353}~
Ở ví dụ thứ 3, Hikaru chơi ~m = 3~ ván cờ. Hai thử thách đều có ~a_i = 1~, do đó ta có thể coi hai thử thách tương đương nhau.
Sau khi thắng ván đấu đầu tiên, một thử thách được thêm vào tập ~S~. Xác suất chiến thắng ván đấu thứ hai là ~\frac{1}{2}~.
Nếu thắng ván thứ hai, Hikaru sẽ thua ván thứ ba, do tất cả các thử thách đều đã được chọn.
Nếu thua ván thứ hai, Hikaru sẽ thắng ván thứ ba, do không có thử thách nào được chọn.
Như vậy kì vọng số ván thắng của Hikaru là:
$$1 + \frac{1}{2} \cdot (1 + 0) + \frac{1}{2} \cdot (0 + 1) = 2$$
Điểm: 3250
Giải đấu Eo Xi Cây có ~2n~ đội tuyển, được đánh số từ ~1~ đến ~2n~ theo thứ tự thực lực giảm dần (~1~ là mạnh nhất). Trước khi giải đấu bắt đầu, có ~m~ cặp đội tuyển là anh em. Trong thời gian diễn ra giải đấu, một số cặp đội tuyển có thể kết thân thành anh em hoặc chấm dứt mối quan hệ anh em của họ. Tuy nhiên, để tránh việc các mối quan hệ có thể ảnh hưởng đến giải đấu, tại một thời điểm bất kỳ trong giải đấu, mỗi đội tuyển chỉ có tối đa một anh em.
Giải đấu gồm hai bảng đấu Baron và Rồng, mỗi bảng bao gồm ~n~ đội. Với tư cách đương kim vô địch thế giới, đội Tê Đỏ được đánh số ~1~ mặc định vào bảng Baron. Trong khi đó, đương kim vô địch quốc nội, đội Hạt Lê được đánh số ~2~ mặc định vào bảng Rồng. Sau đó, các bảng lần lượt chọn đội tuyển, bắt đầu từ bảng Baron. Cụ thể:
Ở mỗi lượt chọn, đội vừa được chọn gần nhất trong bảng sẽ chọn thêm một đội mới.
Nếu đội anh em của đội này chưa được chọn, họ sẽ chọn đội anh em đó.
Nếu không, họ sẽ chọn đội mạnh nhất còn lại chưa được chọn.
Quy trình lặp lại cho đến khi mỗi bảng có đúng ~n~ đội.
Có ~q~ sự kiện xảy ra trong giải đấu. Mỗi sự kiện có thể:
Hai đội kết thân thành anh em.
Hai đội chấm dứt quan hệ anh em.
Ban tổ chức muốn biết một đội bất kỳ đang thi đấu ở bảng nào.
Với mỗi câu hỏi của ban tổ chức, hãy tìm ra bảng mà đội đó đang thi đấu.
Input
Dòng đầu tiên chứa một số nguyên ~t~ (~1 \leq t \leq 100)~ — số bộ test. Mỗi bộ test có dạng như sau:
Dòng đầu tiên chứa hai số nguyên ~n~, ~m~ (~2 \le n \le 10^5~, ~0 \le m \le n~) — số đội mỗi bảng và số cặp anh em ban đầu.
Mỗi trong ~m~ dòng tiếp theo chứa hai số nguyên ~x_i~, ~y_i~ (~1 \le x_i, y_i \le 2n~) — một cặp anh em ban đầu.
Dòng tiếp theo chứa một số nguyên ~q~ (~2 \le q \le 10^5~) — số sự kiện.
Mỗi trong ~q~ dòng tiếp theo mô tả một sự kiện:
~\texttt{+} \; i \; j~: Hai đội ~i~ và ~j~ trở thành anh em (~1 \le i, j \le 2n~, ~i \ne j~). Đảm bảo rằng trước truy vấn này, đội ~i~ không có đội anh em, và đội ~j~ không có đội anh em.
~\texttt{-} \; i \; j~: Hai đội ~i~ và ~j~ không còn là anh em (~1 \leq i, j \le 2n~, ~i \ne j~). Đảm bảo rằng trước truy vấn này, hai đội ~i~ và ~j~ đang là anh em.
~\texttt{?} \; i~: Hỏi hiện tại đội ~i~ đang thi đấu cho bảng nào (~1 \le i \le 2n~).
Đảm bảo rằng tổng của ~n~, tổng của ~m~, và tổng của ~q~ qua mọi test case không vượt quá ~10^5~.
Output
Với mỗi truy vấn dạng ~\mathtt{?} \; i~, in ra:
~\mathtt{0}~ nếu đội ~i~ thuộc bảng Baron.
~\mathtt{1}~ nếu đội ~i~ thuộc bảng Rồng.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~250~ | ~\sum q \le 1000~ |
| 2 | ~1000~ | Tại mọi thời điểm bất kỳ có tối đa ~10~ cặp anh em |
| 3 | ~2000~ | Không có ràng buộc gì thêm |
| Tổng | ~3250~ |
Sample Input 1
2
5 1
1 7
7
+ 4 9
? 3
+ 6 5
- 4 9
- 1 7
? 5
? 6
4 4
2 4
7 1
8 5
3 6
4
- 7 1
? 3
+ 7 1
? 6
Sample Output 1
1
0
1
0
0
Notes
Ở test case thứ nhất, các sự kiện diễn ra như sau.
Ban đầu, cặp anh em duy nhất là ~(1, 7)~.
Sau truy vấn thứ nhất, các cặp anh em là ~(1, 7), (4, 9)~.
Ở truy vấn thứ hai, các đội được sắp xếp như sau, với cặp đội anh em có cùng màu:
| Baron | ~\color{blue}1~ | ~\color{blue}7~ | ~\color{red}4~ | ~\color{red}9~ | ~8~ |
| Rồng | ~2~ | ~3~ | ~5~ | ~6~ | ~10~ |
Đội ~1~ vào bảng Baron.
Đội ~2~ vào bảng Rồng.
Vì đội ~1~ là đội gần nhất vào bảng Baron, và đội ~7~ là anh em của đội ~1~, đội ~7~ vào bảng Baron.
Vì đội ~2~ là đội gần nhất vào bảng Rồng, và đội ~2~ không là anh em với đội nào, đội mạnh nhất chưa được chọn là đội ~3~ vào bảng Rồng.
Vì đội ~7~ là đội gần nhất vào bảng Baron, và đội ~1~ là anh em của đội ~7~ đã thuộc bảng này, đội mạnh chưa được chọn là đội ~4~ vào bảng Baron.
Vì đội ~3~ là đội gần nhất vào bảng Rồng, và đội ~3~ không là anh em với đội nào, đội mạnh nhất chưa được chọn là đội ~5~ vào bảng Rồng.
Vì đội ~4~ là đội gần nhất vào bảng Baron, và đội ~9~ là anh em của đội ~4~, đội ~9~ vào bảng Baron.
Vì đội ~5~ là đội gần nhất vào bảng Rồng, và đội ~5~ không là anh em với đội nào, đội mạnh nhất chưa được chọn là đội ~6~ vào bảng Rồng.
Đội ~8~ vào bảng Baron.
Đội ~10~ vào bảng Rồng.
Vì thế, với truy vấn ~\mathtt{?} \; 3~, ta in ra ~\mathtt{1}~ vì đội ~3~ thuộc bảng Rồng.
Sau truy vấn thứ ba, các cặp anh em là ~(1, 7), (4, 9), (6, 5)~.
Sau truy vấn thứ tư, các cặp anh em là ~(1, 7), (6, 5)~.
Sau truy vấn thứ năm, các cặp anh em là ~(6, 5)~.
Ở truy vấn thứ sáu và bảy, các đội được sắp xếp như sau:
| Baron | ~1~ | ~3~ | ~\color{green}5~ | ~7~ | ~9~ |
| Rồng | ~2~ | ~4~ | ~\color{green}6~ | ~8~ | ~10~ |
Đội ~1~ vào bảng Baron.
Đội ~2~ vào bảng Rồng.
Đội ~3~ vào bảng Baron.
Đội ~4~ vào bảng Rồng.
Đội ~5~ vào bảng Baron.
Vì đội ~4~ là đội gần nhất vào bảng Rồng, và đội ~4~ không là anh em với đội nào, đội mạnh nhất chưa được chọn là đội ~6~ vào bảng Rồng.
Đội ~5~ là đội gần nhất vào bảng Baron. Tuy nhiên, đội anh em của đội ~5~, là đội ~6~, đã được chọn vào bảng Rồng. Vì thế, đội mạnh nhất chưa được chọn là đội ~7~ vào bảng Baron.
Đội ~8~ vào bảng Rồng.
Đội ~9~ vào bảng Baron.
Đội ~10~ vào bảng Rồng.
Vì thế, với truy vấn thứ sáu, ta in ra ~\mathtt{0}~ vì đội ~5~ thuộc bảng Baron; với truy vấn thứ bảy, ta in ra ~\mathtt{1}~ vì đội ~6~ thuộc bảng Rồng.
Điểm: 4000
Bạn được cho xâu ~s~ gồm ~n~ kí tự ~\mathtt{g}~, ~\mathtt{e}~, hoặc ~\mathtt{?}~, thoả mãn điều kiện rằng ~s_1 = s_n = \mathtt{g}~. Hãy đếm số mảng ~a~ có độ dài ~n~ thoả mãn các điều kiện sau.
Mọi phần tử của ~a~ đều là ~1~ hoặc ~-1~.
Gọi ~p_i = \sum_{j=1}^{i} a_j~ là tổng của ~i~ phần tử đầu tiên của ~a~, với quy ước ~p_0 = 0~. Thế thì:
~p_i \ge 0~ với mọi ~1 \le i \le n~.
Với mọi ~1 \le i \le n~ mà ~s_i = \mathtt{g}~, thì ta phải có $$\max(p_0, p_1, \dots, p_i) > \max(p_0, p_1, \dots, p_{i - 1}).$$
Với mọi ~1 \le i \le n~ mà ~s_i = \mathtt{e}~, thì ta phải có $$\max(p_0, p_1, \dots, p_i) = \max(p_0, p_1, \dots, p_{i - 1}).$$
Input
Dòng đầu tiên chứa số nguyên ~t~ (~1 \le t \le 1000~) – số lượng test case. Mô tả của mỗi test case như sau.
Dòng đầu tiên chứa số nguyên ~n~ (~1 \le n \le 4000~) — độ dài của ~s~.
Dòng thứ hai chứa xâu ~s~ (~|s| = n, s_i \in \{\mathtt{g}, \mathtt{e}, \mathtt{?}\}, s_1 = s_n = \mathtt{g}~).
Đảm bảo rằng tổng ~n^2~ qua tất cả các test case không quá ~30 \cdot 10^6~.
Output
Với mỗi test case, in ra một số nguyên là số lượng mảng ~a~ thoả mãn các điều kiện trên đề bài. Do số này có thể rất lớn, hãy in ra đáp án dưới modulo ~998\,244\,353~.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~500~ | ~n \le 1000~ với mọi test case, ~\sum n^2 \le 10^6~ |
| 2 | ~500~ | ~s~ không chứa kí tự ~\mathtt{?}~ với mọi test case |
| 3 | ~750~ | ~n \le 1000~ với mọi test case |
| 4 | ~2250~ | Không có ràng buộc gì thêm |
| Tổng | ~4000~ |
Sample Input 1
7
4
ge?g
4
g??g
4
gegg
6
geeeeg
10
g?eg??eegg
10
g????????g
27
geeeee?e??e????e?e?ee?eg??g
Sample Output 1
1
2
0
1
3
49
460
Notes
Ở test case thứ nhất, mảng duy nhất thoả mãn là ~a = [1, -1, 1, 1]~, với ~p = [1, 0, 1, 2]~:
Tại ~i = 1~, ta có ~\max(p_0, p_1) = 1 > 0 = \max(p_0)~, thoả mãn ~s_1 = \mathtt{g}~.
Tại ~i = 2~, ta có ~\max(p_0, p_1, p_2) = 1 = 1 = \max(p_0, p_1)~, thoả mãn ~s_2 = \mathtt{e}~.
Tại ~i = 4~, ta có ~\max(p_0, p_1, p_2, p_3, p_4) = 2 > 1 = \max(p_0, p_1, p_2, p_3)~, thoả mãn ~s_4 = \mathtt{g}~.
Ở test case thứ hai, hai mảng thoả mãn là:
~a = [1, 1, 1, 1]~. Ở đây, ~p = [1, 2, 3, 4]~.
~a = [1, -1, 1, 1]~. Ở đây, ~p = [1, 0, 1, 2]~.
Ở test case thứ tư, mảng duy nhất thoả mãn là ~a = [1, -1, 1, -1, 1, 1]~ với ~p = [1, 0, 1, 0, 1, 2]~.
Điểm: 5000
Tahp vừa khám phá ra một thuật toán thú vị với các ngăn xếp đơn điệu. Cậu bắt đầu với một dãy số yêu thích ~p_1, p_2, \ldots, p_n~ là hoán vị của các số nguyên từ ~1~ đến ~n~ và một dãy vô hạn các ngăn xếp (stack) được đánh số từ ~1~. Ban đầu, các ngăn xếp đều rỗng.
Cậu định nghĩa thuật toán đệ quy để thêm một phần tử có giá trị ~x~ vào ngăn xếp thứ ~i~ như sau:
function add(i, x):
while (stack[i] is not empty) and (x < top(stack[i])) do
y := top(stack[i])
pop(stack[i])
add(i + 1, y)
end while
push(stack[i], x)
end function
Tahp sẽ lần lượt thêm các phần tử của dãy ~p~ vào ngăn xếp số ~1~, tức là gọi liên tiếp các thao tác: ~\texttt{add(1, $p_1$)}, \texttt{add(1, $p_2$)}, \ldots, \texttt{add(1, $p_n$)}~
Sau khi quá trình trên kết thúc, cậu ghi lại trạng thái của toàn bộ dãy ~n~ ngăn xếp, ký hiệu là ~s(p)~. Tahp nhận thấy rằng có nhiều dãy ~p~ khác nhau nhưng đều tạo ra cùng một trạng thái.
Giờ đây, Tahp muốn thử thách bạn tìm một hoán vị ~q_1, q_2, \ldots, q_n~ sao cho:
~q > p~ theo thứ tự từ điển~^*~
~s(q) = s(p)~
Nếu không tồn tại hoán vị nào như vậy, hãy kết luận rằng không thể tìm được. Hai trạng thái được xem là giống nhau nếu với mọi ngăn xếp, dãy các phần tử trong ngăn xếp đó giống hệt nhau theo thứ tự từ dưới lên trên.
Hơn nữa, Tahp có những yêu cầu khác nhau cho hoán vị ~q~ cần tìm, được mô tả bằng số nguyên ~k \in \{0, 1\}~:
Nếu ~k = 0~: ~q~ là một hoán vị bất kỳ thoả mãn.
Nếu ~k = 1~: ~q~ là hoán vị nhỏ nhất theo thứ tự từ điển trong tất cả các hoán vị thoả mãn. Nói cách khác, không tồn tại hoán vị ~q'~ nào thoả mãn các điều kiện trên mà ~q' < q~
——————————————————
~^*~Với hai hoán vị ~p~ và ~q~ khác nhau cùng có độ dài ~n~, ta nói ~q~ nhỏ hơn ~p~ theo thứ tự từ điển nếu ~q_i < p_i~, với ~i~ là vị trí đầu tiên mà ~p_i \neq q_i~.
Input
Dòng đầu tiên chứa số nguyên ~t~ (~1 \le t \le 10\,000~) – số lượng test case. Mô tả của mỗi test case như sau.
Dòng đầu tiên chứa hai số nguyên ~n~, ~k~ ~(1 \le n \le 2 \cdot 10^5; k \in \{0, 1\})~ — độ dài dãy ~p~ và yêu cầu của Tahp.
Dòng thứ hai chứa ~n~ số nguyên ~p_1, p_2, \ldots, p_n~ ~(1 \le p_i \le n)~ — dãy số yêu thích của Tahp.
Đảm bảo dãy ~p~ là một hoán vị của các số nguyên từ ~1~ đến ~n~, và tổng ~n~ trong tất cả các test case không vượt quá ~10^5~.
Output
Với mỗi test case, nếu không tồn tại hoán vị nào thoả mãn yêu cầu, in ra ~\mathtt{-1}~. Ngược lại, in ra trên một dòng hoán vị ~q~ tìm được. Với ~k = 0~, nếu có nhiều hoán vị ~q~ thỏa mãn, hãy in ra hoán vị ~q~ bất kỳ.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~1000~ | ~\sum n \le 2000, k = 0~ |
| 2 | ~1000~ | ~\sum n \le 2000~ |
| 3 | ~1000~ | ~k = 0~ |
| 4 | ~2000~ | Không có ràng buộc gì thêm |
| Tổng | ~5000~ |
Sample Input 1
4
3 1
1 3 2
5 0
5 4 3 2 1
6 0
3 4 1 6 2 5
6 1
3 4 1 6 2 5
Sample Output 1
3 1 2
-1
4 3 1 2 6 5
4 1 3 2 6 5
Notes
Ta kí hiệu ngăn xếp thứ ~i~ là ~s_i~, và ta sẽ không quan tâm đến các ngăn xếp rỗng.
Ở test case thứ nhất, ta xét quá trình thêm hoán vị ~[1, 3, 2]~ như sau:
Khi ~\texttt{add(1, $p_1 = 1$)}~, ta có ~s_1 = [1]~.
Khi ~\texttt{add(1, $p_2 = 3$)}~, vì ~3~ lớn hơn đầu ~s_1~ là ~1~, ta thêm ~3~ vào ~s_1~. ~s_1 = [1, 3]~.
Khi ~\texttt{add(1, $p_3 = 2$)}~:
Vì ~2~ nhỏ hơn đầu ~s_1~ là ~3~, ta pop ~3~ ra khỏi ~s_1~ và thực hiện ~\texttt{add(2, $3$)}~. Sau thao tác này, ~s_1 = [1], s_2 = [3]~.
Bây giờ ~2~ lớn hơn đầu ~s_1~ là ~1~, ta thêm ~2~ vào ~s_1~. Sau thao tác này, ~s_1 = [1, 2], s_2 = [3]~.
Cuối cùng, ta có ~s_1 = [1, 2], s_2 = [3]~. Đây cũng là trạng thái của ~p = [1, 3, 2]~.
Bây giờ, ta xét quá trình thêm hoán vị ~[3, 1, 2]~ như sau:
Khi ~\texttt{add(1, $p_1 = 3$)}~, ta có ~s_1 = [3]~.
Khi ~\texttt{add(1, $p_2 = 1$)}~:
Vì ~1~ nhỏ hơn đầu ~s_1~ là ~3~, ta pop ~3~ ra khỏi ~s_1~ và thực hiện ~\texttt{add(2, $3$)}~. Sau thao tác này, ~s_1 = [], s_2 = [3]~.
Bây giờ ~s_1~ rỗng, nên ta thêm ~1~ vào ~s_1~. Sau thao tác này, ~s_1 = [1], s_2 = [3]~.
Khi ~\texttt{add(1, $p_3 = 2$)}~, vì ~2~ lớn hơn đầu ~s_1~ là ~1~, ta thêm ~2~ vào ~s_1~. ~s_1 = [1, 2], s_2 = [3]~.
Cuối cùng, ta có ~s_1 = [1, 2], s_2 = [3]~. Đây cũng là trạng thái của ~p = [3, 1, 2]~.
Vì thế, ta thấy ~s([1, 3, 2]) = s([3, 1, 2])~. Ta có thể chứng minh được rằng không có hoán vị nào có giá trị từ điển giữa ~[1, 3, 2]~ và ~[3, 1, 2]~ mà cho ra trạng thái tương tự. Vì thế, do ~k = 1~ ở test case này, đáp án duy nhất được chấp nhận là ~q = [3, 1, 2]~.