Thuyền Giấy
Xem dạng PDFSau một ngày dài vui chơi với những fan hâm mộ cua của mình, Saba chuẩn bị trở về ngọn hải đăng trên một chiếc thuyền giấy nhỏ băng qua biển. Muốn tiễn Saba lần cuối trước khi trời tối, những chú cua quyết định xếp hàng dọc theo lộ trình chèo thuyền của cô để tạm biệt. Vì số lượng fan của Saba đã vượt quá một triệu, những chú cua cần phải đứng đủ thưa để Saba có thể chèo thuyền về nhà an toàn.
Lộ trình chèo thuyền được mô hình dưới dạng lưới với ~k~ hàng và ~2^{60}~ cột. Các hàng được đánh số từ ~0~ đến ~k - 1~ từ trên xuống dưới, và các cột được đánh số từ ~0~ đến ~2^{60} - 1~, bắt đầu từ bờ biển. Bờ biển nằm trước cột ~0~, và nhà của Saba nằm ngay sau cột ~2^{60} - 1~. Nắm được điều này, những chú cua đã phối hợp để xếp hàng như sau:
Các chú cua chọn ra hai số ~l~ và ~r~, sao cho ~0 \le l \le r < 2^{60}~;
Đối với mỗi cột ~i~ từ ~l~ đến ~r~, một chú cua sẽ đứng ở hàng thứ ~j~ nếu và chỉ nếu bit thứ ~j~ từ bên phải của ~i~ là ~0~ (nói cách khác, ~\left\lfloor \frac{i}{2^j} \right\rfloor~ chẵn);
Không có chú cua nào đứng ở bất kỳ ô nào khác của lưới.
Saba phải điều hướng qua các fan của mình để về nhà như sau.
Bắt đầu từ bờ biển, Saba có thể chọn một ô trống ở cột thứ ~0~ để đặt chiếc thuyền giấy của mình.
Saba có thể về đến nhà nếu cô ấy di chuyển được đến một ô trống ở cột thứ ~(2^{60} - 1)~.
Chiếc thuyền có thể di chuyển từ một ô sang ô khác nếu hai ô đó có cạnh chung.
Chiếc thuyền không được rời khỏi lưới.
Và vì chiếc thuyền cực kỳ mong manh, nó sẽ hỏng nếu nó đi vào cùng một ô chứa một chú cua.
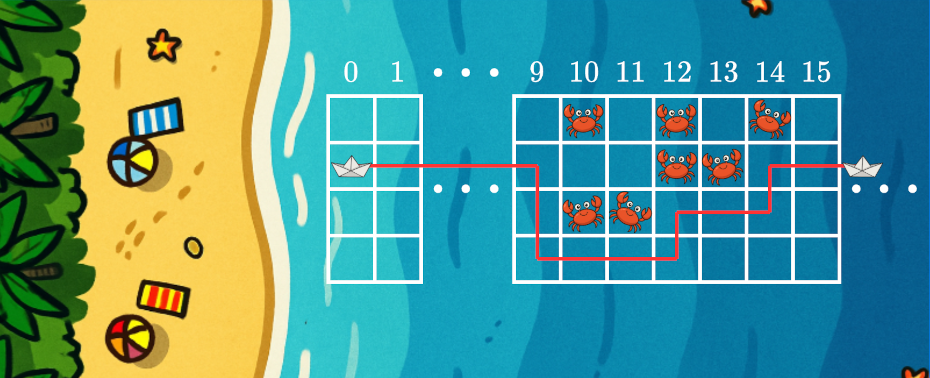
Minh họa cho test case đầu tiên: ~l = 10~, ~r = 14~, ~k = 4~. Saba có thể trở về nhà an toàn.
Thấy được sự tận tâm của những người hâm mộ, Saba rất cảm động! Tuy nhiên, cô nổi tiếng là kém toán, vì vậy cô không chắc liệu mình có thể về nhà an toàn hay không. Giúp Saba xác định xem có một lối đi an toàn về nhà hay không, dựa trên cách sắp xếp của những chú cua.
Input
Dòng đầu tiên chứa một số nguyên dương ~t~ (~1 \leq t \leq 10\,000~) – số lượng testcase.
Dòng đầu tiên và duy nhất của mỗi testcase chứa 3 số ~l~, ~r~, ~k~ (~0 \leq l \leq r < 2^{60}~, ~1 \leq k \leq 60~) – khoảng cột mà những chú cua sẽ đứng, và số lượng hàng.
Output
Với mỗi testcase, in ra ~\mathtt{YES}~ nếu có một lối đi để Saba có thể an toàn về nhà, hoặc ~\mathtt{NO}~ nếu không.
Scoring
Tổng điểm cho bài này là ~500~.
Sample Input 1
6
10 14 4
52 54 7
100 200 60
999999999999999999 1000000000000000000 1
6 6 1
15 29 3
Sample Output 1
YES
YES
NO
NO
NO
NO
Notes
Test case đầu tiên đã được giải thích qua hình minh họa ở phần đề bài.
Trong test case thứ hai: ~l = 52~, ~r = 54~, ~k = 7~. Dưới đây là minh họa cho vị trí đứng của các chú cua và cách Saba di chuyển qua:
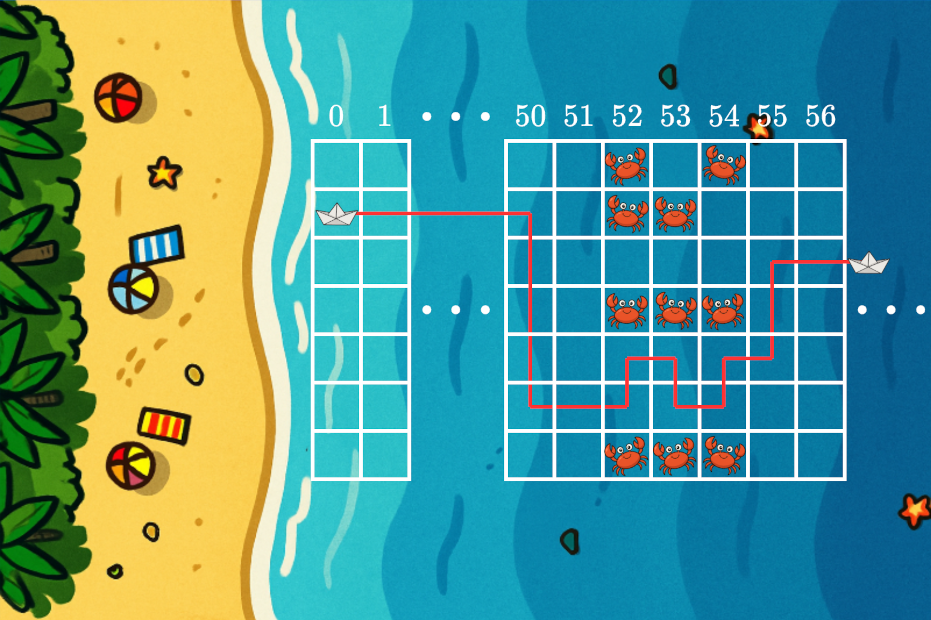
Trong các test case còn lại, tất cả mọi con đường về nhà đều phải đi qua ít nhất một chú cua, do đó không có cách để Saba có thể di chuyển về nhà một cách an toàn.
Bình luận
mò ra được công thức do mô phỏng bằng nháp nhưng không biết giải thích sao, nhưng đến một giá trị nào đó cua sẽ cản hoàn toàn một đoạn, ví dụ cột 32 thì bị chắn 5 hàng đầu, cột 64 bị chắn 6 hàng đầu cột 2^n bị chắn n hàng, ta dùng công thức với mỗi hàng để xác định có ra được không và ra kết quả. Cụ thể tại hàng j(0 <= j < k):
l // (1 << j) % 2 == 0 bị chắn đúng j hàng nên không qua hàng j được bỏ qua
nếu không thì l + (1 << j) - l % (1 << j) - 1 sẽ xét nếu có thể đi qua r tại j + 1 được lập tức in "YES", ngược lại duyệt hết mà ko có là "NO"
bài này theo mình thì khá khó cho người mới
Bình luận này đã bị ẩn vì có quá nhiều phản ứng tiêu cực. Nhấn để xem.