Đồ Thị, Hoán Vị và Xâu Nhị Phân
Xem dạng PDFBạn được cho đồ thị có hướng liên thông yếu~^*~ gồm ~n~ đỉnh và ~m~ cạnh có dạng ~u_i \to v_i~ với ~1 \le i \le m~, một xâu nhị phân ~s~ có độ dài là ~m~, và một hoán vị ~p~ của các giá trị từ ~1~ tới ~n~. Bạn được thực hiện thao tác sau không hay nhiều lần:
- Chọn một chỉ số ~i~ từ ~1~ tới ~m~. Hoán đổi giá trị của ~p_{u_i}~ và ~p_{v_i}~, và đồng thời đảo chiều cạnh thứ ~i~ của đồ thị (nếu cạnh này đang là ~u_i \to v_i~ thì sẽ biến thành ~v_i \to u_i~, và ngược lại).
Bạn muốn thực hiện các thao tác trên cho đến khi cả hai điều kiện sau được thoả mãn.
Hoán vị ~p~ thoả mãn ~p_i = i~ với mọi ~1 \le i \le n~.
Với mọi cạnh ~u_i \to v_i~ (~1 \le i \le m~) ở đồ thị ban đầu, nếu ~s_i = \mathtt{0}~ thì cạnh này không bị đảo chiều, ngược lại thì cạnh này bị đảo chiều.
Bạn cần xác định xem có tồn tại dãy thao tác nào để thoả mãn hai điều kiện trên hay không. Nếu có, hãy tìm một dãy thao tác như vậy với tối đa ~4n^2~ thao tác.
————————————
~^*~ Một đồ thị có hướng được gọi là liên thông yếu khi và chỉ khi nếu thay thế toàn bộ cạnh có hướng ~u \to v~ của đồ thị thành cạnh vô hướng ~(u, v)~, thì đồ thị vô hướng thu được là liên thông.
Input
Dòng đầu tiên chứa số nguyên ~t~ (~1 \le t \le 10\,000~) – số lượng test case. Mô tả của mỗi test case như sau.
Dòng đầu tiên chứa hai số nguyên ~n~ và ~m~ (~2 \le n \le 500, n - 1 \le m \le \frac{n(n-1)}{2}~) — số lượng đỉnh và cạnh của đồ thị. Đảm bảo rằng đồ thị đã cho liên thông yếu.
Dòng thứ hai chứa một xâu nhị phân ~s~ (~|s| = m, s_i \in \{\mathtt{0}, \mathtt{1}\}~).
Dòng thứ ba chứa ~n~ số nguyên ~p_1, p_2, \ldots, p_n~ (~1 \le p_i \le n~) là các phần tử của hoán vị mà bạn được cho.
Dòng thứ ~i~ trong ~m~ dòng tiếp theo chứa hai số nguyên ~u_i~ và ~v_i~ (~1 \le u_i, v_i \le n, u_i \neq v_i~) mô tả cạnh ~u_i \to v_i~ trên đồ thị ban đầu. Đảm bảo rằng giữa hai đỉnh bất kì trên đồ thị, tồn tại tối đa một cạnh giữa chúng.
Đảm bảo rằng tổng ~n^2~ qua tất cả các test case không quá ~250\,000~.
Output
Với mỗi test case, nếu không tồn tại dãy thao tác nào để thoả mãn cả hai điều kiện như đề bài, in ra ~\mathtt{NO}~ trên một dòng. Ngược lại
Ở dòng đầu tiên, in ra ~\mathtt{YES}~.
Ở dòng thứ hai, in ra ~k~ (~0 \le k \le 4n^2~) là số lượng thao tác cần dùng.
Ở dòng thứ ba, in ra ~k~ số nguyên ~i_1, i_2, \dots, i_k~ (~1 \le i_j \le m~) là các chỉ số mà sẽ bạn sẽ áp dụng thao tác lên. Nếu ~k = 0~, bạn có thể chọn in ra một dòng trống, hoặc bạn không in ra dòng này.
Ta có thể chứng minh rằng với giới hạn đã có, nếu tồn tại bất kì dãy thao tác nào để thoả mãn đề bài, thì cũng tồn tại dãy thao tác thoả mãn đề bài mà sử dụng tối đa ~4n^2~ thao tác.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~1000~ | ~m = n - 1~, đồng thời cạnh thứ ~i~ của đồ thị nối giữa đỉnh ~i~ và ~i + 1~ với mọi ~1 \le i \le m~ |
| 2 | ~1250~ | Không có ràng buộc gì thêm |
| Tổng | ~2250~ |
Sample Input 1
4
5 7
0100101
2 4 1 3 5
5 1
2 4
2 3
1 3
4 3
1 4
4 5
5 7
0100101
3 2 1 5 4
5 1
2 4
2 3
1 3
4 3
1 4
4 5
4 6
000000
1 2 3 4
1 2
1 3
1 4
2 3
2 4
3 4
3 2
11
1 2 3
1 2
2 3
Sample Output 1
YES
5
1 5 7 1 2
NO
YES
0
YES
6
1 2 1 2 1 2
Notes
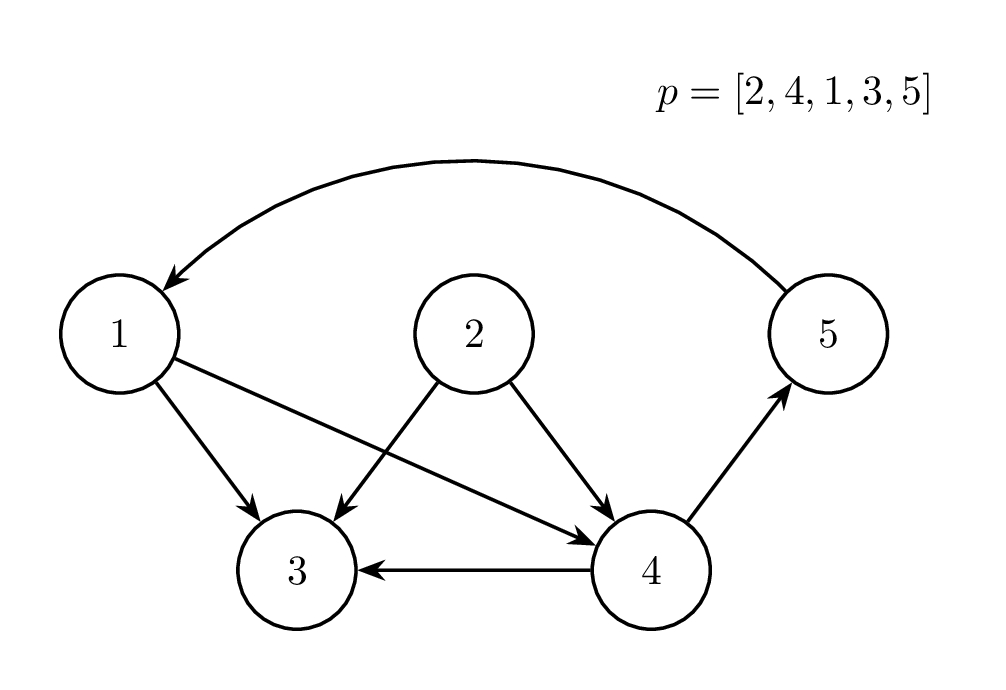
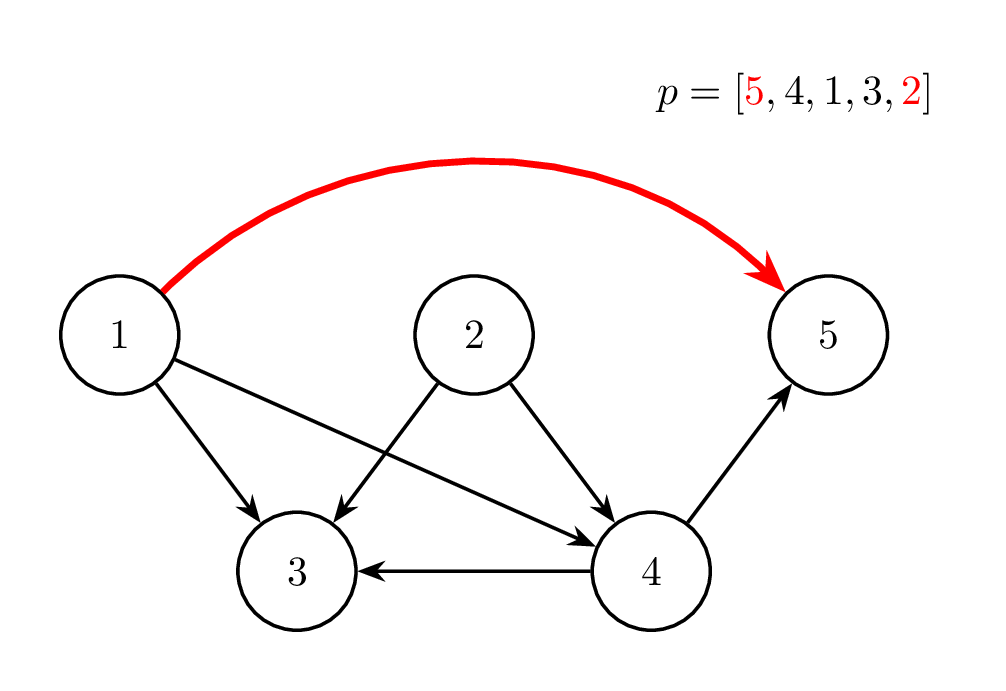
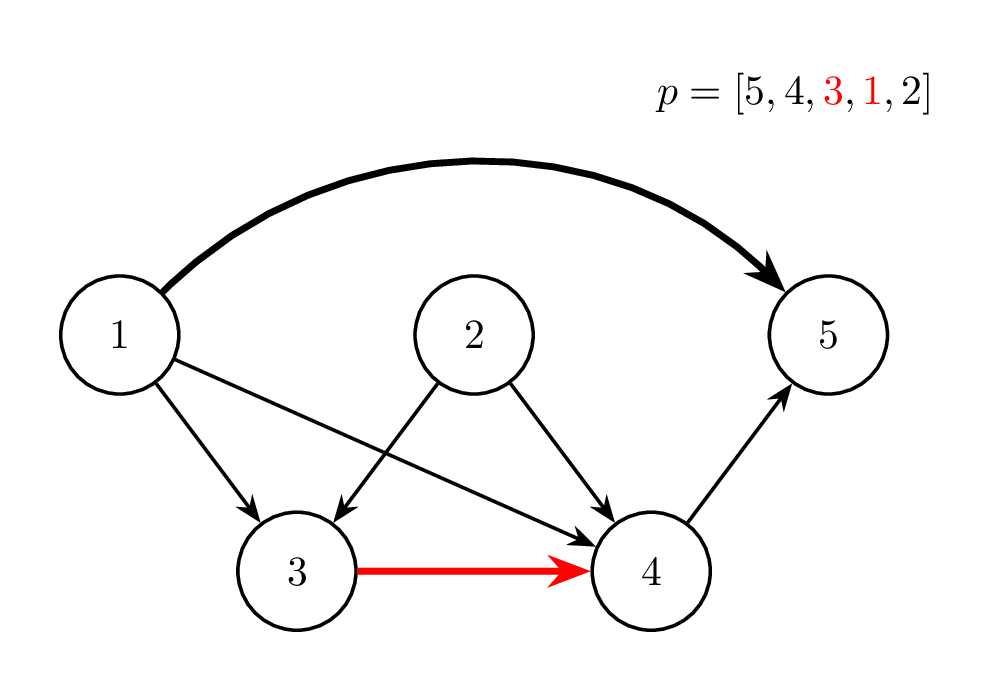
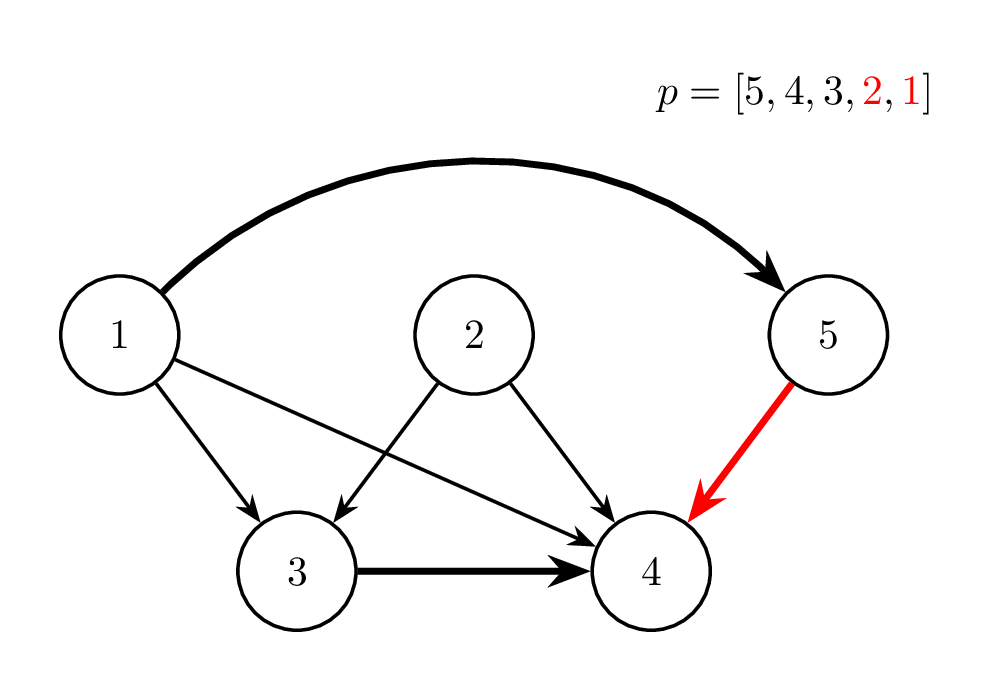
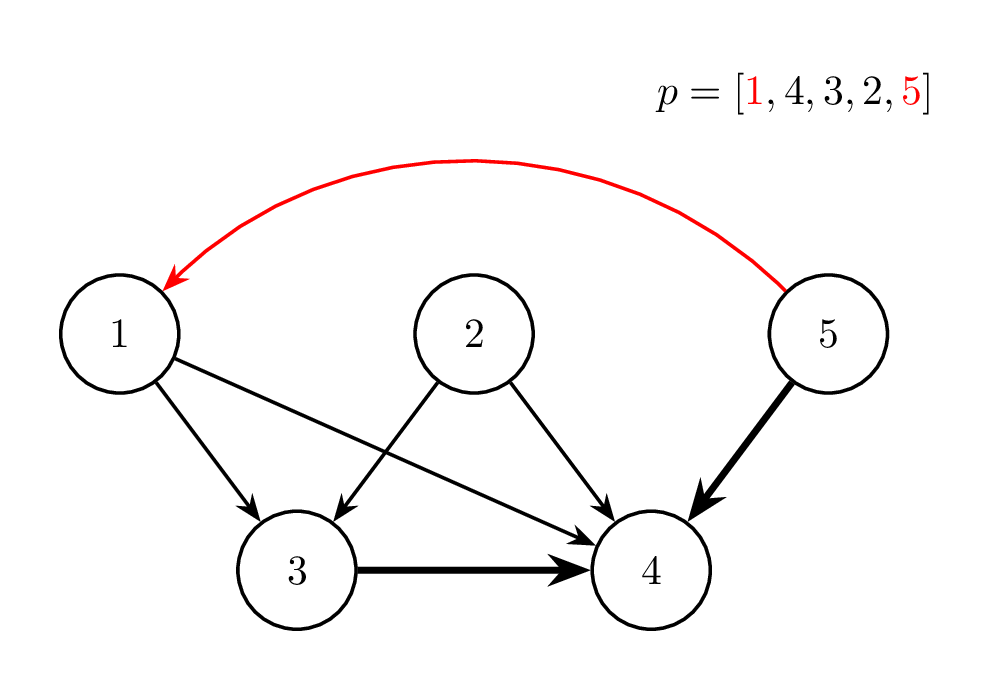
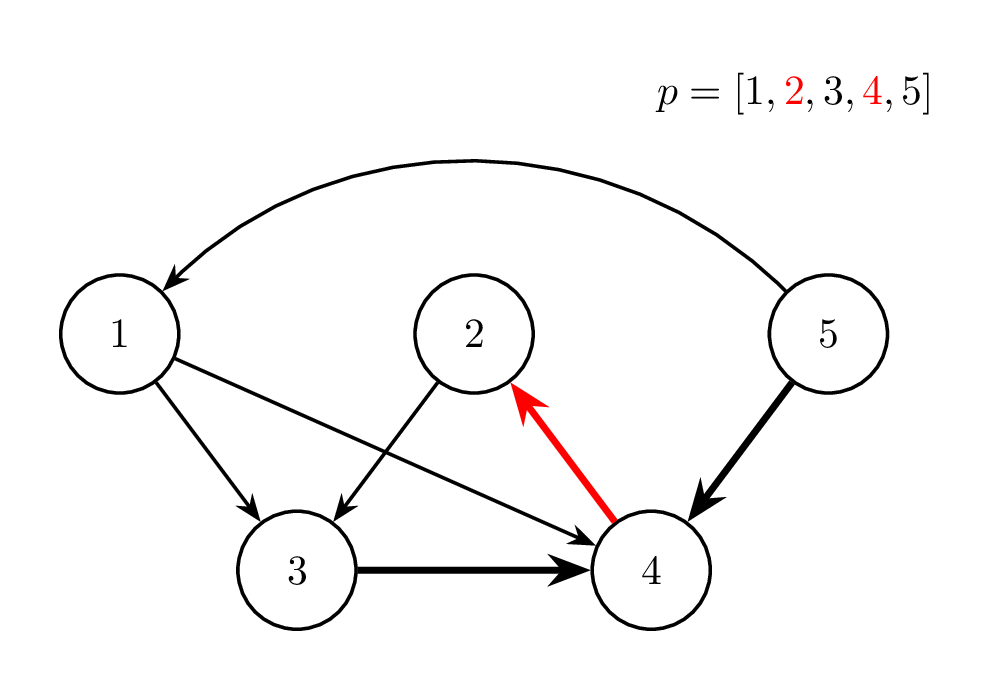
Sáu hình dưới đây minh hoạ cho các phép biến đổi trong test case thứ nhất. Ở mỗi hình, màu đỏ chỉ cạnh được đảo chiều và hai phần tử được hoán đổi ở từng phép thao tác. Ngoài ra, cạnh in đậm chỉ những cạnh đã bị đảo chiều so với đồ thị ban đầu.
Trạng thái ban đầu |
Thao tác 1: ~i = 1~ |
Thao tác 2: ~i = 5~ |
Thao tác 3: ~i = 7~ |
Thao tác 4: ~i = 1~ |
Thao tác 5: ~i = 2~ |
Bình luận