VNOI CUP 2023 - Vòng loại thứ hai
Điểm: 500
Ban nhạc Đoàn Kết gồm có ~4~ thành viên là HG, NI, RY và IK. Ngoài việc luyện tập rất chăm chỉ, thi thoảng ban nhạc có tổ chức một số hoạt động vui chơi, để các thành viên trong ban nhạc được gần gũi với nhau hơn, tăng tinh thần đoàn kết của ban nhạc.
Hôm nay các bạn quyết định chơi trốn tìm, và lần này các bạn sẽ chơi trốn tìm trên sân trường. Sân trường có thể coi là một bảng có kích thước ~n \times m~, với các hàng được đánh số từ ~1~ đến ~n~, và các cột được đánh số từ ~1~ đến ~m~. Khi nhìn từ trên cao xuống sân trường, có thể thấy ô ở hàng thứ ~i~ và cột ~j~ đang có màu là ~c_{i,j}~.
Vì tính tình rụt rè, nhút nhát, bạn HG nhận là người trốn. Hiểu tính cách của HG, ba bạn NI, RY và IK đoán rằng HG sẽ nằm cuộn tròn thành một viên đá. Viên đá này sẽ có hình dáng của một hình vuông kích thước ~2 \times 2~ và sẽ chiếm ~4~ ô trên sân trường.
Ngoài ra viên đá này sẽ có màu sắc rất đặc trưng. Viên đá sẽ có ~3~ màu phân biệt, sau cho màu của ~2~ ô ở cột thứ hai giống nhau. Cụ thể hơn, nếu viên đá chiếm ~4~ ô ~(i, j)~, ~(i + 1, j)~, ~(i, j + 1)~ và ~(i + 1, j + 1)~ thì:
~c_{i, j} \ne c_{i + 1, j}~,
~c_{i, j} \ne c_{i, j + 1}~,
~c_{i + 1, j} \ne c_{i + 1, j + 1}~,
~c_{i, j + 1} = c_{i + 1, j + 1}~.

Minh hoạ cho ví dụ thứ tư. Hình vuông có viền in đậm trong hình thể hiện một ví trị hợp lệ viên đá HG.
Cho màu sắc của các ô trên sân trường. Hãy đoán xem HG có đang trốn trên sân trường hay không.
Input
Dòng đầu tiên gồm hai số nguyên ~n~ và ~m~ (~2 \le n, m \le 500~) – kích thước của sân trường.
Dòng thứ ~i~ trong ~n~ dòng tiếp theo chứa một xâu kí tự có độ dài ~m~ bao gồm các kí tự tiếng Anh in hoa. Kí tự thứ ~j~ thể hiện màu ~c_{i, j}~.
Output
In ra "YES" nếu như tồn tại một hình vuông có kích thước ~2 \times 2~ trên sân trường trùng với mô tả viên đá HG. In ra "NO" trong trường hợp ngược lại.
Scoring
Số điểm nhận được nếu bạn giải thành công bài toán này là ~500~ điểm.
Sample Input 1
2 2
BP
YP
Sample Output 1
YES
Sample Input 2
3 3
VOI
IOI
TST
Sample Output 2
YES
Sample Input 3
5 5
QWERT
YUIOP
ASDFG
HJKLZ
XCVBN
Sample Output 3
NO
Sample Input 4
16 16
WWWWWWWWWWWWWWWW
WPPWWWWWWWWWWWWW
PWWPWWWPPWWWWWWW
WWWWBPPPPPPWWWWW
WWWWYPPPPPPPWWWW
WWWPPPPPPPPPPWWW
WWWPGGGPPGGGPWWW
WWWPPPGPPGPPPWWW
WWWPPGPPPPGPPWWW
WWWPGPPPPPPGPWWW
WWWPBPPPPPPBPWWW
WWPPPPPPPPPPPPWW
WWPPPPPPPPPPPPWW
WPPPPWPPPPWPPPPW
WPPPWWWPPWWWPPPW
WWWWWWWWWWWWWWWW
Sample Output 4
YES
Notes
Trong ví dụ đầu tiên, sân trường có kích thước ~2 \times 2~. Có duy nhất một hình vuông ~2 \times 2~ trên sân trường có mô tả khớp với viên đá HG.
Ví dụ thứ tư đã có hình minh họa trên đề bài.
Điểm: 1250
Trung đang tham dự lớp học tin của thầy giáo Chung, và chủ đề của buổi học hôm nay là ước chung lớn nhất. Tiếng giảng bài của thầy bắt đầu vang lên.
"Với hai số nguyên ~a~ và ~b~ bất kì không đồng thời bằng ~0~, ước chung lớn nhất của ~a~ và ~b~ được định nghĩa là số nguyên ~x~ lớn nhất mà cả ~a~ và ~b~ đều chia hết cho ~x~. Ước chung lớn nhất của ~a~ và ~b~ được kí hiệu là ~\gcd(a, b)~, tương ứng với các chữ cái đầu tiên của khái niệm này khi dịch sang tiếng Anh (Greatest Common Divisor). Ví dụ, ~\gcd(8, 12) = 4~, ~\gcd(5, 7) = 1~, ~\gcd(0, 100) = 100~."
Đang say sưa giảng bài, thầy Chung bỗng phát hiện Trung đang nghịch điện thoại. Thấy vậy, thầy Chung trở nên tức giận và yêu cầu Trung phải giải được bài tập mà thầy đưa ra, nếu không thì cậu sẽ bị đuổi khỏi lớp. Ngặt nỗi, bài toán mà thầy Chung đưa ra lại vô cùng hóc búa:
"Cho dãy số ~a~ gồm ~n~ số nguyên dương ~a_1, a_2, \ldots, a_n~. Cậu hãy viết một đoạn mã để đổi chỗ các phần tử của dãy ~a~ theo một thứ tự bất kì, sao cho nếu định nghĩa dãy ~b~ gồm ước chung lớn nhất giữa các cặp số liên tiếp của dãy ~a~ (~b_i = \gcd(a_i, a_{i+1})~ với ~1 \le i < n~) thì giá trị lớn thứ nhì của dãy ~b~ là lớn nhất có thể. Cậu không cần phải in ra dãy ~a~ sau khi đổi chỗ, mà chỉ cần đưa ra giá trị lớn thứ nhì của dãy ~b~ tối đa tìm được."
Hãy giúp Trung giải bài toán trên, đồng thời giúp cậu thoát khỏi cơn thịnh nộ của thầy Chung nhé.
Input
Mỗi input sẽ gồm nhiều test cases. Dòng đầu tiên của input gồm số nguyên dương ~t~ (~1 \le t \le 1000~) — số test cases của bài toán. Sau đây là mô tả của các test cases.
Dòng đầu tiên của mỗi test case gồm số nguyên dương ~n~ (~3 \le n \le 100~) — số phần tử của dãy ~a~.
Dòng tiếp theo của mỗi test case gồm ~n~ số nguyên dương ~a_1, a_2, \dots, a_n~ (~1 \le a_i \le 100~) — các phần tử của dãy ~a~.
Output
Với mỗi test case, in ra một số nguyên duy nhất là số lớn thứ nhì của dãy ~b~ tối đa tìm được.
Scoring
Số điểm nhận được nếu bạn giải thành công bài toán này là ~1250~ điểm.
Sample Input 1
3
3
20 6 12
4
9 6 10 5
5
2 3 5 7 11
Sample Output 1
4
3
1
Notes
Ở ví dụ thứ nhất, nếu ta đổi dãy ~a~ thành ~[20, 12, 6]~ thì dãy ~b~ ứng với dãy ~a~ là ~[\gcd(20, 12), \gcd(12, 6)] = [4, 6]~, phần tử lớn thứ nhì của dãy ~b~ là ~4~. Có thể chứng minh rằng không có cách sắp xếp nào cho kết quả tốt hơn.
Ở ví dụ thứ hai, nếu ta giữ nguyên dãy ~a~ như ban đầu (~[9, 6, 10, 5]~) thì dãy ~b~ ứng với dãy ~a~ là ~[3, 2, 5]~, phần tử lớn thứ nhì của dãy ~b~ là ~3~. Có thể chứng minh rằng không có cách sắp xếp nào cho kết quả tốt hơn.
Ở ví dụ thứ ba, mọi phần tử của dãy ~a~ đều là số nguyên tố nên với mọi cách đổi chỗ dãy ~a~ thì dãy ~b~ ứng với dãy ~a~ đều sẽ là ~[1, 1, 1, 1]~. Do đó phần tử lớn nhì của dãy ~b~ luôn là ~1~.
Điểm: 1500
Lộc đang nghiên cứu về một thuật toán sắp xếp mới có tên gọi Vectorized Neural-network in Ordering Intergers (VNOI) – thuật toán ứng dụng công nghệ mạng thần kinh vector hóa để tối ưu hóa việc sắp xếp mảng số nguyên. Sau một thời gian rất dài cất công nghiên cứu, cuối cùng Lộc cũng đã có một bước tiến mới trong thao tác sắp xếp mảng số nguyên!
Lộc đang có một mảng số nguyên gồm ~n~ phần tử ~a_1, a_2, \ldots, a_n~. Với công nghệ mới vừa được nghiên cứu, Lộc có thể thực hiện thao tác sau đây rất nhiều lần một cách nhanh chóng:
- Chọn ra hai chỉ số ~i~ và ~j~ (~1 \le i, j \le n~) sao cho ~i + j~ chia hết cho ~k~. Sau đó thực hiện tráo đổi giá trị của ~a_i~ và ~a_j~.
Tuy đây là thao tác rất nhanh với công nghệ vừa được nghiên cứu, Lộc vẫn thắc mắc rằng liệu có thể sử dụng thao tác này (không hoặc nhiều lần) để sắp xếp mảng ~a~ không giảm hay không. Hãy giúp Lộc kiểm tra xem có cách nào sử dụng thao tác trên để sắp xếp mảng ~a~ thoả yêu cầu không nhé!
Input
Dòng đầu tiên gồm số nguyên ~t~ (~1 \le t \le 10\,000~) – số lượng các test case. Mô tả của mỗi test case như sau.
Dòng đầu tiên gồm hai số nguyên ~n~ và ~k~ (~1 \le n \le 200\,000~, ~1 \le k \le n~) – độ dài mảng ~a~ của Lộc và tham số ~k~ cho thao tác.
Dòng thứ hai chứa ~n~ số nguyên ~a_1, a_2, \ldots, a_n~ (~1 \le a_i \le 10^9~).
Dữ liệu đảm bảo tổng của các số ~n~ trong tất cả các test case không quá ~200\,000~.
Output
Với mỗi test case, hãy in ra "YES" (không bao gồm ngoặc nháy), nếu như tồn tại một dãy thao tác để sắp xếp mảng ~a~ không giảm. Ngược lại hãy in ra "NO" (không bao gồm ngoặc nháy).
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | 500 | ~k = 2~ |
| 2 | 1000 | Không có giới hạn gì thêm |
| Tổng | 1500 |
Sample Input 1
3
3 2
1 2 3
4 2
1 4 3 2
3 2
2 1 2
Sample Output 1
YES
YES
NO
Sample Input 2
3
3 3
1 2 3
3 3
2 1 3
3 3
3 2 1
Sample Output 2
YES
YES
NO
Sample Input 3
2
10 1
10 9 8 7 6 5 4 3 2 1
10 10
10 9 8 7 6 5 4 3 2 1
Sample Output 3
YES
NO
Notes
Trong test ví dụ đầu tiên:
Ở test case đầu tiên, mảng ~a~ đã được sắp xếp.
Ở test case thứ hai, mảng ~a = [1, 4, 3, 2]~ và ~k = 2~. Ta có thể chọn chỉ số ~i = 2~ và ~j = 4~ (do ~2 + 4 = 6~ chia hết cho ~k = 2~) và tráo đổi ~a_2~ và ~a_4~ để thu được mảng ~a = [1, 2, 3, 4]~.
Ở test case thứ ba, mảng ~a = [2, 1, 2]~ và ~k = 2~. Cặp chỉ số ~(i, j)~ hợp lệ duy nhất là ~(1, 3)~, tuy nhiên vì ~a_1 = a_3 = 2~, khi tráo đổi chúng, ta thu được mảng ban đầu. Do đó không có cách nào để sắp xếp mảng.
Trong test ví dụ thứ hai:
Ở test case đầu tiên, mảng ~a~ đã được sắp xếp.
Ở test case thứ hai, mảng ~a = [2, 1, 3]~ và ~k = 3~. Ta có thể chọn chỉ số ~i = 1~ và ~j = 2~ (do ~1 + 2 = 3~ chia hết cho ~k = 3~) và tráo đổi ~a_1~ và ~a_2~ để thu được ~a = [1, 2, 3]~.
Ở test case thứ ba, mảng ~a = [3, 2, 1]~ và ~k = 3~. Cặp chỉ số ~(i, j)~ hợp lệ duy nhất là ~(1, 2)~, và khi tráo đổi ~a_1~ và ~a_2~ ta thu được mảng ~a = [2, 1, 3]~. Ta không thể thu được mảng ~a~ khác, do đó không có cách nào để sắp xếp mảng.
Điểm: 2500
Vì muốn rời xa những ồn ào của chốn phồn hoa đô thị, Lộc đã quyết định dành toàn bộ kì nghỉ hè của mình để khám phá khu rừng nằm ở vùng rìa quê mình. Để hoàn toàn hòa mình vào không khí thiên nhiên, Lộc cần xây một ngôi nhà ở trong khu rừng và sống tại đây trong suốt thời gian nghỉ hè.
Khu rừng có thể được miêu tả bằng một lưới chữ nhật gồm ~n~ dòng và ~m~ cột. Các dòng được đánh số từ ~1~ đến ~n~ từ bắc xuống nam, các cột được đánh số từ ~1~ đến ~m~ từ tây sang đông, ô nằm ở dòng ~i~ và cột ~j~ được gọi là ô ~(i, j)~. Kì lạ thay, mỗi ô trên lưới chữ nhật có chứa đúng một cây gỗ sồi, cây ở ô ~(i, j)~ có chiều cao là ~h_{i,j}~.
Kế hoạch xây nhà của Lộc sẽ bắt đầu bằng việc xây dựng hàng rào bao bọc xung quanh ngôi nhà. Trước tiên, Lộc cần chọn ra bốn cây gỗ sồi nằm ở bốn ô ~(r_1, c_1)~, ~(r_1, c_2)~, ~(r_2, c_1)~, ~(r_2, c_2)~ sao cho ~1 \le r_1 < r_2 \le n~, ~1 \le c_1 < c_2 \le m~. Nói cách khác, bốn ô được chọn sẽ là bốn góc của một hình chữ nhật có góc trái trên ở ô ~(r_1, c_1)~ và góc phải dưới ở ô ~(r_2, c_2)~. Đồng thời, sau khi Lộc thực hiện kế hoạch chặt cây thì hàng rào tạo thành cần phải khép kín.
Cụ thể, kế hoạch chặt cây của Lộc, và điều kiện tương ứng để đảm bảo hàng rào tạo thành được khép kín như sau:
Chặt cây ở ô ~(r_1, c_1)~ đổ theo hướng đông. Cây ở ô ~(r_1, c_1)~ cần có chiều cao ít nhất là ~c_2 - c_1~.
Chặt cây ở ô ~(r_1, c_2)~ đổ theo hướng nam. Cây ở ô ~(r_1, c_2)~ cần có chiều cao ít nhất là ~r_2 - r_1~.
Chặt cây ở ô ~(r_2, c_2)~ đổ theo hướng tây. Cây ở ô ~(r_2, c_2)~ cần có chiều cao ít nhất là ~c_2 - c_1~.
Chặt cây ở ô ~(r_2, c_1)~ đổ theo hướng bắc. Cây ở ô ~(r_2, c_1)~ cần có chiều cao ít nhất là ~r_2 - r_1~.
Để cân nhắc việc lựa chọn các cây gỗ sồi cần chặt, Lộc cần biết có bao nhiêu số cách chọn bộ bốn cây thỏa mãn yêu cầu như trên. Hãy giúp Lộc thực hiện việc này nhé.
Input
Dòng đầu tiên gồm số nguyên dương ~n~ và ~m~ (~2 \leq n, m~; ~n \times m \leq 80\,000~) — kích thước của lưới chữ nhật mô tả khu rừng.
Dòng thứ ~i~ trong ~n~ dòng tiếp theo gồm ~m~ số nguyên ~h_{i,1}, h_{i,2}, \ldots, h_{i,m}~ (~1 \le h_{i,j} \le 10^9~) — chiều cao của các cây trong khu rừng.
Output
In ra tổng số cách chọn bộ bốn cây thỏa yêu cầu đề bài.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | 500 | ~n\times m \le 1000~ |
| 2 | 750 | ~h_{i, j} \le 10~ với mọi ~1 \le i \le n, 1 \le j \le m~ |
| 3 | 1250 | Không có ràng buộc gì thêm |
| Tổng | 2500 |
Sample Input 1
2 4
4 3 2 1
1 2 3 4
Sample Output 1
6
Sample Input 2
3 4
3 1 2 2
1 2 1 2
2 2 1 3
Sample Output 2
9
Sample Input 3
4 3
3 1 2
1 2 2
2 1 1
2 2 3
Sample Output 3
10
Notes
Ở ví dụ đầu tiên, tất cả các hình chữ nhật con đều có bốn góc thỏa mãn điều chặt cây ở đề bài.
Ở ví dụ thứ hai, ngoài ~6~ hình chữ nhật con có kích thước ~2 \times 2~ thì còn ~3~ cách chọn bộ bốn cây như sau:
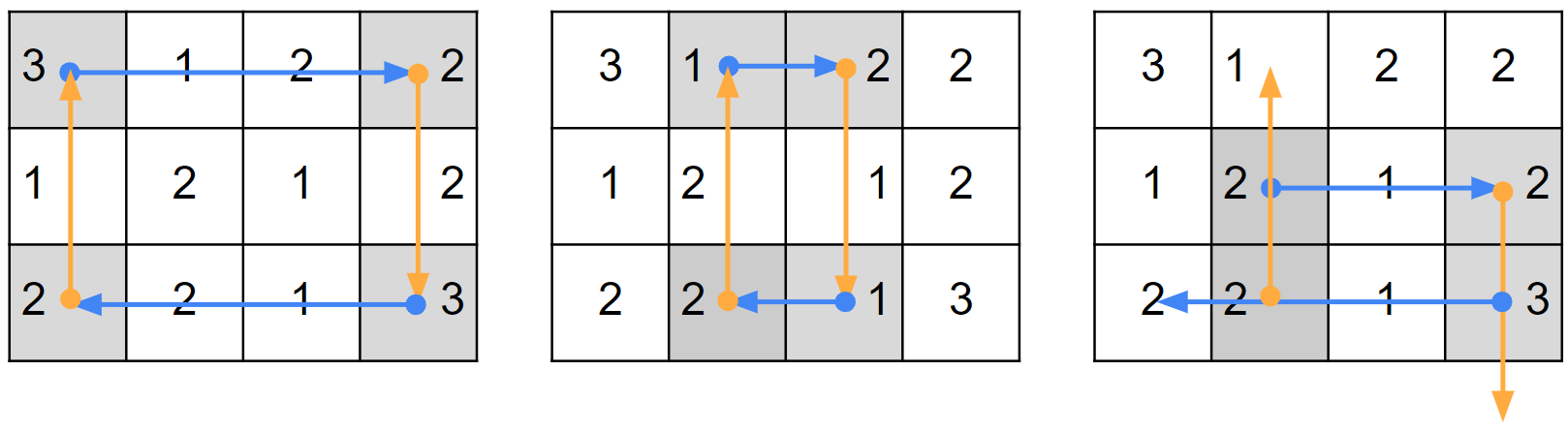
Hình vẽ minh họa ví dụ thứ hai.
Điểm: 2750
Nhanh nhạy khi tấn công và phòng thủ tầm xa, mang trong mình phong thái của một nhà hoạch định chiến lược, đặc biệt phát huy năng lực khi thế trận thông thoáng, đó là tất cả những đặc điểm của một quân nhẹ chủ lực trên bàn cờ vua — quân tượng.
Với các đặc điểm tuyệt vời trên, việc khéo léo để sử dụng quân tượng trong mỗi ván cờ là hết sức quan trọng. Để tập luyện, Trung đã đầu tư mua về hẳn một bàn cờ vua kích thước ~n~ ~\times~ ~m~ chỉ để học cách sử dụng các quân tượng. Cậu đã đặt trước ~k~ quân tượng trên bàn cờ, quân thứ ~i~ được đặt ở ô có vị trí (~x_i~, ~y_i~) và muốn đặt thêm nhiều quân tượng vào bàn cờ nhất, sao cho không tồn tại hai quân nào có thể ăn nhau. Hai quân tượng chỉ có thể ăn nhau khi chúng nằm trên cùng một đường chéo.
Vì số lượng cách đặt có thể rất lớn, Trung lại muốn thử hết tất cả các cách để rút ra nhiều kinh nghiệm cho bản thân. Bạn hãy giúp Trung tính số lượng quân tượng nhiều nhất có thể đặt thêm vào bàn cờ và số cách để thực hiện điều đó, in ra phần dư của số cách sau khi chia cho ~10^9+7~.
Input
Dòng đầu tiên chứa ba số nguyên ~n~, ~m~ và ~k~ (~1 \leq n \leq 16, 1 \leq m \leq 100, 0 \leq k \leq 100~) — kích thước của bàn cờ vua và số quân tượng đã có sẵn trên bàn cờ.
Dòng thứ ~i~ trong ~k~ dòng tiếp theo chứa hai số nguyên ~x_i~, ~y_i~ (~1 \leq x_i \leq n~, ~1 \leq y_i \leq m~) — vị trí của quân tượng thứ ~i~.
Dữ liệu đảm bảo ~k~ quân tượng Trung đã đặt không tồn tại hai quân có thể ăn nhau.
Output
Một dòng duy nhất chứa hai số nguyên là số lượng quân tượng tối đa có thể đặt thêm và số cách để đặt thêm tối đa các con tượng modulo ~10^9 + 7~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | 500 | ~1 \leq n, m \leq 4~ |
| 2 | 750 | ~1 \leq n \leq 8, 1 \leq m \leq 100~ |
| 3 | 1500 | Không có ràng buộc gì thêm |
| Tổng | 2750 |
Sample Input 1
3 3 1
2 2
Sample Output 1
2 2
Sample Input 2
4 4 2
1 1
4 1
Sample Output 2
4 4
Sample Input 3
8 100 4
2 5
8 6
8 99
5 1
Sample Output 3
102 857399411
Notes
Các ô màu xanh chứa quân tượng màu đen là những quân tượng có sẵn trên bàn cờ. Những quân tượng màu trắng là những quân tượng được đặt thêm.
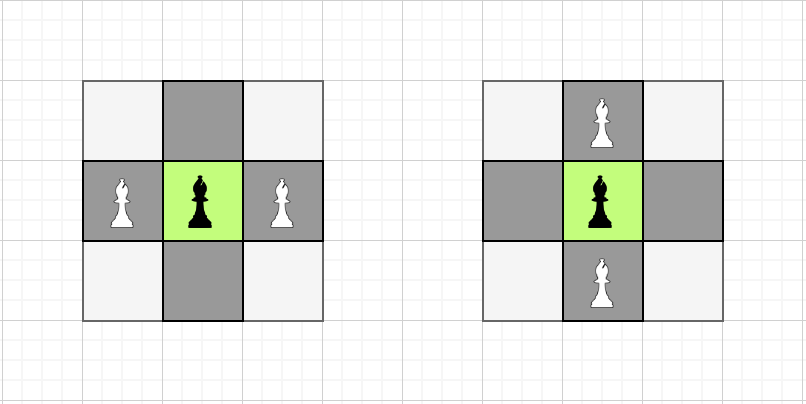
Minh họa cho ví dụ đầu tiên.
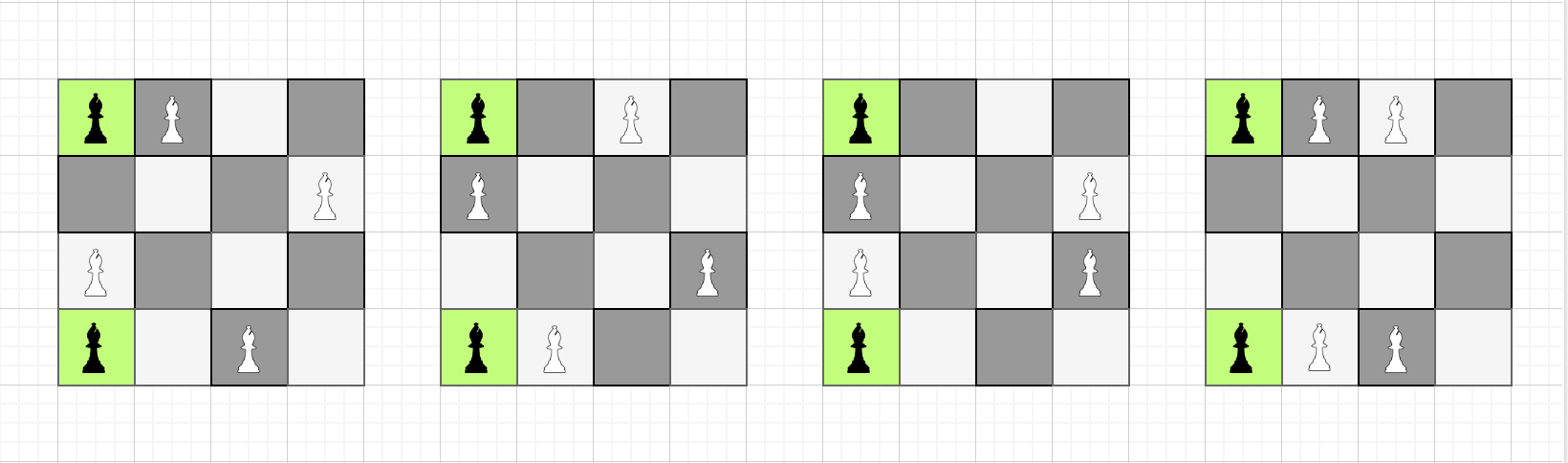
Minh họa cho ví dụ thứ hai
Điểm: 3500
Nhân dịp Giáng Sinh, Kuroni và ~n~ người bạn chơi một phiên bản của trò Secret Santa với Kuroni làm quản trò. Trò chơi sẽ diễn ra trong ~d~ ngày (với ~d~ được chọn bởi Kuroni); diễn biến mỗi ngày xảy ra như sau:
Đầu tiên, Kuroni chọn ~k~ bạn khác nhau ~u_1, u_2, \dots, u_k~, rồi đề xuất với một giá trị thực dương ~w~. Lưu ý là ~k~, ~w~, và ~u_1, u_2, \dots, u_k~ có thể có giá trị khác nhau qua từng ngày.
Sau đó, mỗi bạn được chọn sẽ mua một món đồ có giá trị đúng bằng ~w~.
Cuối cùng, các bạn tặng món đồ mình đã mua theo vòng tròn: ~u_1~ tặng món quà của mình cho ~u_2~, ~u_2~ tặng món quà của mình cho ~u_3~, ..., ~u_k~ tặng món quà của mình cho ~u_1~.
Để gắn kết ~n~ người bạn của mình lại gần nhau hơn, Kuroni đã lên sẵn một danh sách gồm ~m~ cặp ~(u, v)~, với mong muốn rằng khi kết thúc trò chơi này, bạn thứ ~u~ phải gửi cho bạn thứ ~v~ ít nhất một món quà; ngoài ra, với những cặp ~(x, y)~ không nằm trong danh sách của anh ấy, bạn thứ ~x~ không được phép gửi quà cho bạn thứ ~y~ (vì như thế sẽ khiến bạn ~y~ hiểu nhầm ý định của bạn ~x~).
Dĩ nhiên, Kuroni cũng không muốn nảy sinh tình cảm không trong sáng giữa ~n~ bạn của mình, nên anh ấy muốn rằng khi kết thúc trò chơi, với mọi bạn ~u~, tổng giá trị quà ~u~ nhận được từ các bạn đã tặng quà cho ~u~ là như nhau. Nói cách khác, nếu ~v~ và ~t~ là hai bạn đã tặng cho ~u~ ít nhất một món quà, thì tổng giá trị quà ~v~ tặng ~u~ phải bằng với tổng giá trị quà ~t~ tặng ~u~ (nếu không thì ~u~ sẽ ưu ái bạn tặng nhiều quà hơn).
Kuroni nghĩ nát óc vẫn chưa tìm được cách dàn xếp trò chơi để đạt được nguyện vọng của mình. Bạn hãy giúp anh ấy nhé!
Input
Dòng đầu tiên bao gồm hai số nguyên dương ~n~ và ~m~ (~1 \le n, m \le 200~) — số lượng bạn của Kuroni và số lượng cặp đôi trong danh sách của anh.
Dòng thứ ~i~ trong ~m~ dòng tiếp theo bao gồm hai số nguyên dương ~u_i~ và ~v_i~ (~1 \le u_i, v_i \le n~) — biểu diễn cặp thứ ~i~ trong danh sách của Kuroni.
Dữ liệu đảm bảo rằng không tồn tại cặp nhau xuất hiện lại nhiều lần trong danh sách, cũng như không tồn tại cặp nào nối một bạn về chính bạn ấy.
Output
Ở dòng đầu tiên, in ra "YES" (không chứa ngoặc nháy) nếu tồn tại một cách dàn xếp trò chơi để đạt được ý muốn của Kuroni; nếu không, in ra "NO" (không chứa ngoặc nháy).
Nếu dòng đầu tiên in ra "YES", bạn cần in ra ở dòng thứ hai số ~d~ không quá ~500~ là số lượng ngày mà mọi người sẽ chơi. Ta có thể chứng minh được rằng dưới giới hạn của bài này, nếu tồn tại một cách dàn xếp trò chơi thỏa mãn điều kiện thì cũng tồn tại một cách mà không cần chơi quá ~500~ ngày.
Tiếp theo, bạn cần in ra ~d~ dòng, với dòng thứ ~i~ biểu diễn ngày chơi thứ ~i~. Ở mỗi dòng:
Đầu tiên, in ra số thực dương không quá ~10^{15}~ ~w~ là giá trị quà được đề xuất ở ngày này. Ta có thể chứng minh được rằng dưới giới hạn của bài này, nếu tồn tại một cách dàn xếp trò chơi thỏa mãn điều kiện thì cũng tồn tại một cách mà giá trị quà ở mỗi ngày không quá ~10^{15}~.
Tiếp theo, in ra số nguyên dương ~k~ là số lượng bạn được chọn chơi ở ngày thứ ~i~.
Cuối cùng, in ra ~k~ số nguyên dương đôi một khác nhau ~u_1, u_2, \dots, u_k~ biểu diễn các bạn được chọn (~1 \le u_j \le n~ với mọi ~1 \le j \le k~).
Các giá trị trên cần được in ra trên cùng một dòng, tách nhau bởi dấu cách.
Định nghĩa ~f(u \to v)~ là tổng giá trị quà ~u~ đã gửi cho ~v~ xuyên suốt trò chơi. Trình chấm sẽ nhận diện cách dàn xếp trò chơi được in ra là hợp lệ nếu như với mọi bạn ~u~ và hai bạn ~v~ và ~t~ có gửi quà cho ~u~, sai số tương đối giữa tổng giá trị quà ~v~ gửi cho ~u~ và tổng giá trị quà ~t~ gửi cho ~u~ không vượt quá ~10^{-6}~; nói cách khác, nếu ~x = f(v \to u)~ và ~y = f(t \to u)~ thì ~\frac{|x - y|}{\min(x, y)} \le 10^{-6}~.
Dữ liệu được sinh ra sẽ thỏa mãn rằng nếu tồn tại một cách dàn xếp hợp lệ thì sẽ tồn tại một cách dàn xếp sao cho với hai cặp ~(u, v)~ và ~(x, y)~ trong danh sách, tỉ lệ của ~f(u \to v)~ và ~f(x \to y)~ không vượt quá ~10^{10}~. Tuy nhiên, đáp án bạn in ra không cần phải thỏa mãn điều kiện này.
Scoring
Nếu coi như danh sách của Kuroni tương ứng với một đồ thị có hướng ~G~ gồm ~n~ đỉnh ~m~ cạnh, với mỗi cặp ~(u, v)~ tương ứng với một cạnh có hướng ~u \to v~ trong ~G~ thì
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | 1000 | Mọi cạnh ~u \to v~ của ~G~ thuộc tối đa ~1~ chu trình đơn của ~G~ |
| 2 | 1000 | Mọi cạnh ~u \to v~ của ~G~ thỏa mãn ~u \lt v~ ngoại trừ cạnh ~n \to 1~ |
| 3 | 1500 | Không có ràng buộc gì thêm |
| Tổng | 3500 |
Sample Input 1
5 7
1 2
2 3
3 1
2 4
3 5
4 5
5 2
Sample Output 1
YES
3
1.0 3 1 2 3
0.5 3 2 3 5
0.5 3 2 4 5
Sample Input 2
3 4
1 2
2 1
1 3
2 3
Sample Output 2
NO
Sample Input 3
6 6
1 2
2 3
3 1
4 5
5 6
6 4
Sample Output 3
YES
2
0.3 3 1 2 3
0.6 3 5 6 4
Notes
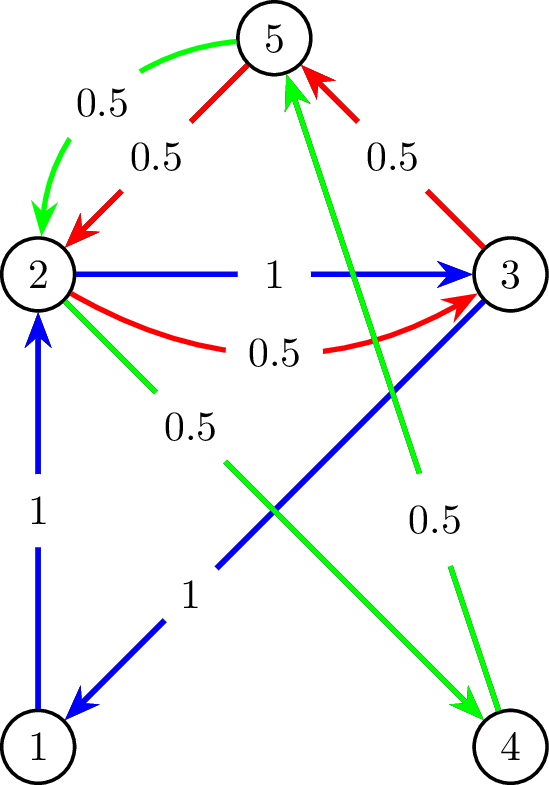
Ở ví dụ đầu tiên, ta có các hình minh họa sau cho đồ thị ~G~ ban đầu, cách dàn xếp trò chơi, và tổng giá trị quà mà các bạn đã tặng cho nhau; ba ngày chơi được biểu diễn bởi ba màu khác nhau.
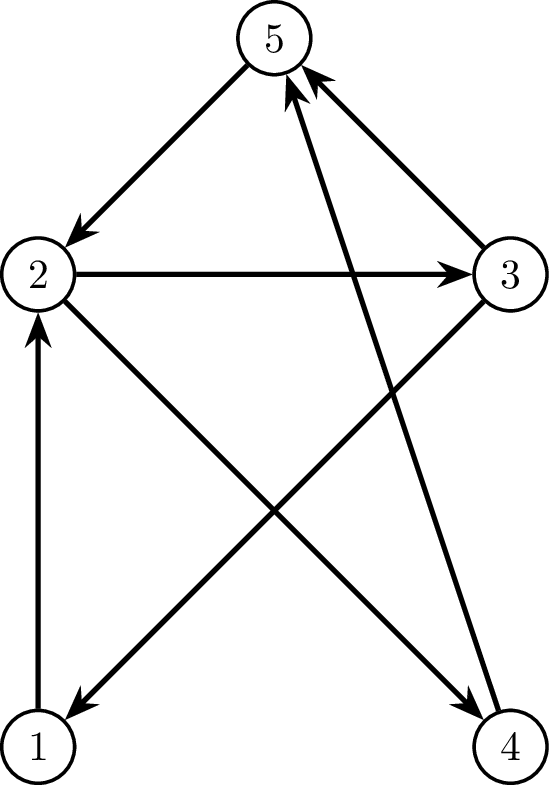 |
 |
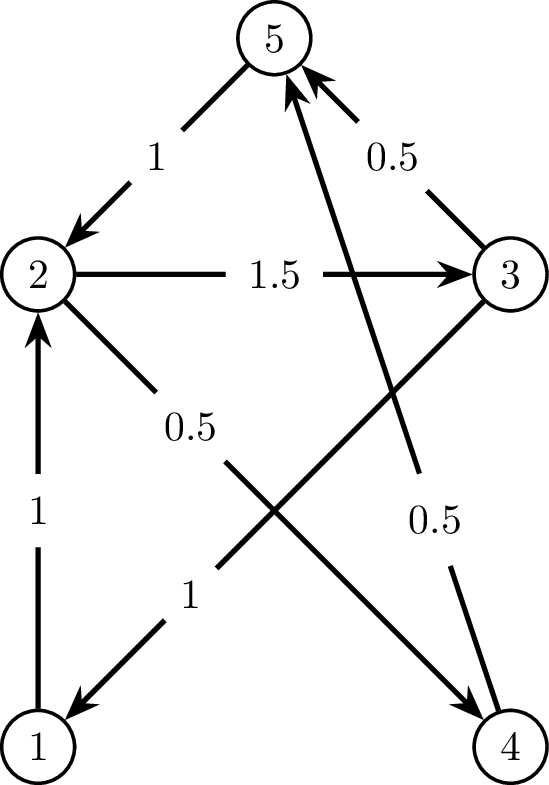 |
Đồ thị ~G~ ban đầu, cách dàn xếp trò chơi, và tổng giá trị quà mà các bạn đã tặng cho nhau.
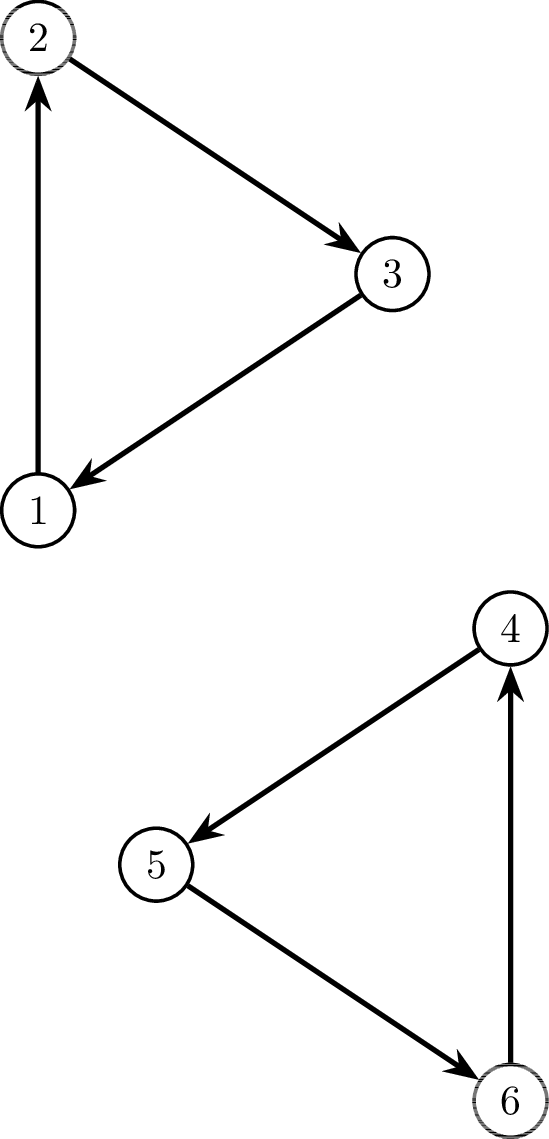
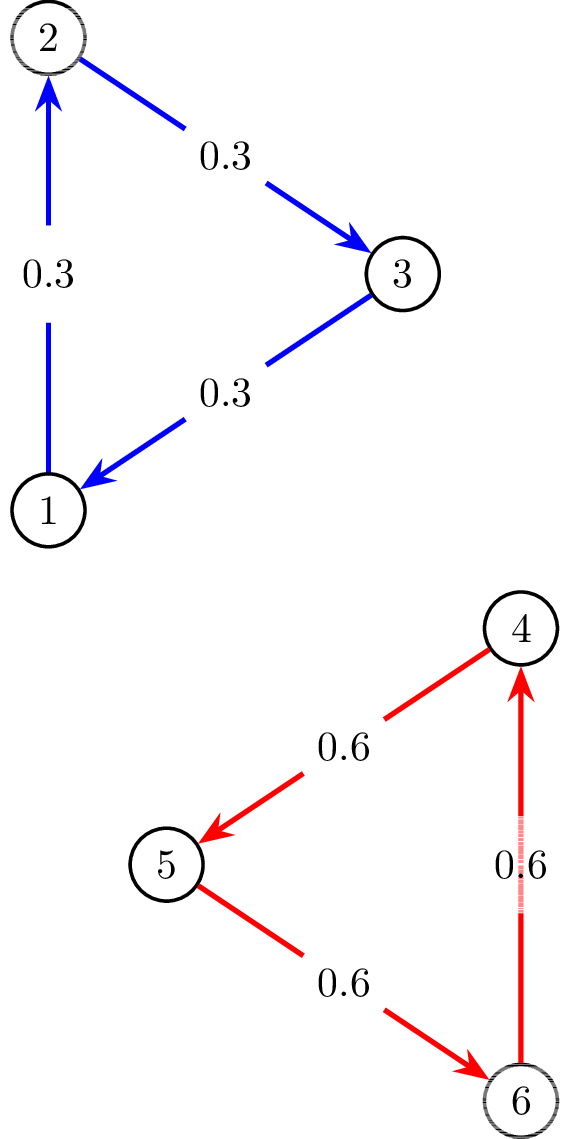
Tương tự, ta có ba hình minh họa sau cho ví dụ thứ ba.
 |
 |
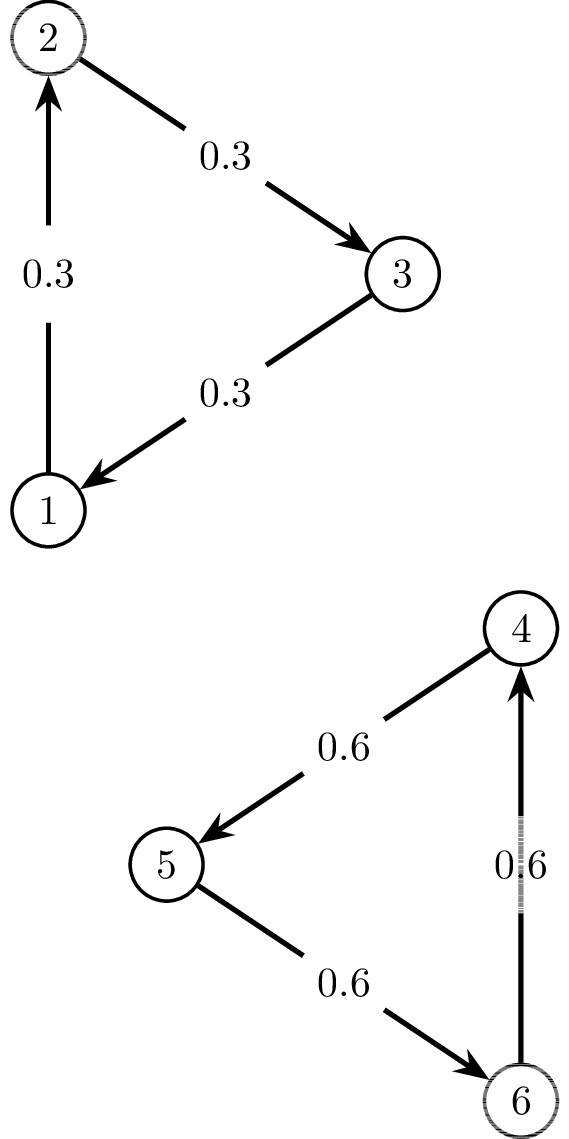 |
Đồ thị ~G~ ban đầu, cách dàn xếp trò chơi, và tổng giá trị quà mà các bạn đã tặng cho nhau.