Khu rừng ma thuật
Xem dạng PDFVì muốn rời xa những ồn ào của chốn phồn hoa đô thị, Lộc đã quyết định dành toàn bộ kì nghỉ hè của mình để khám phá khu rừng nằm ở vùng rìa quê mình. Để hoàn toàn hòa mình vào không khí thiên nhiên, Lộc cần xây một ngôi nhà ở trong khu rừng và sống tại đây trong suốt thời gian nghỉ hè.
Khu rừng có thể được miêu tả bằng một lưới chữ nhật gồm ~n~ dòng và ~m~ cột. Các dòng được đánh số từ ~1~ đến ~n~ từ bắc xuống nam, các cột được đánh số từ ~1~ đến ~m~ từ tây sang đông, ô nằm ở dòng ~i~ và cột ~j~ được gọi là ô ~(i, j)~. Kì lạ thay, mỗi ô trên lưới chữ nhật có chứa đúng một cây gỗ sồi, cây ở ô ~(i, j)~ có chiều cao là ~h_{i,j}~.
Kế hoạch xây nhà của Lộc sẽ bắt đầu bằng việc xây dựng hàng rào bao bọc xung quanh ngôi nhà. Trước tiên, Lộc cần chọn ra bốn cây gỗ sồi nằm ở bốn ô ~(r_1, c_1)~, ~(r_1, c_2)~, ~(r_2, c_1)~, ~(r_2, c_2)~ sao cho ~1 \le r_1 < r_2 \le n~, ~1 \le c_1 < c_2 \le m~. Nói cách khác, bốn ô được chọn sẽ là bốn góc của một hình chữ nhật có góc trái trên ở ô ~(r_1, c_1)~ và góc phải dưới ở ô ~(r_2, c_2)~. Đồng thời, sau khi Lộc thực hiện kế hoạch chặt cây thì hàng rào tạo thành cần phải khép kín.
Cụ thể, kế hoạch chặt cây của Lộc, và điều kiện tương ứng để đảm bảo hàng rào tạo thành được khép kín như sau:
Chặt cây ở ô ~(r_1, c_1)~ đổ theo hướng đông. Cây ở ô ~(r_1, c_1)~ cần có chiều cao ít nhất là ~c_2 - c_1~.
Chặt cây ở ô ~(r_1, c_2)~ đổ theo hướng nam. Cây ở ô ~(r_1, c_2)~ cần có chiều cao ít nhất là ~r_2 - r_1~.
Chặt cây ở ô ~(r_2, c_2)~ đổ theo hướng tây. Cây ở ô ~(r_2, c_2)~ cần có chiều cao ít nhất là ~c_2 - c_1~.
Chặt cây ở ô ~(r_2, c_1)~ đổ theo hướng bắc. Cây ở ô ~(r_2, c_1)~ cần có chiều cao ít nhất là ~r_2 - r_1~.
Để cân nhắc việc lựa chọn các cây gỗ sồi cần chặt, Lộc cần biết có bao nhiêu số cách chọn bộ bốn cây thỏa mãn yêu cầu như trên. Hãy giúp Lộc thực hiện việc này nhé.
Input
Dòng đầu tiên gồm số nguyên dương ~n~ và ~m~ (~2 \leq n, m~; ~n \times m \leq 80\,000~) — kích thước của lưới chữ nhật mô tả khu rừng.
Dòng thứ ~i~ trong ~n~ dòng tiếp theo gồm ~m~ số nguyên ~h_{i,1}, h_{i,2}, \ldots, h_{i,m}~ (~1 \le h_{i,j} \le 10^9~) — chiều cao của các cây trong khu rừng.
Output
In ra tổng số cách chọn bộ bốn cây thỏa yêu cầu đề bài.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | 500 | ~n\times m \le 1000~ |
| 2 | 750 | ~h_{i, j} \le 10~ với mọi ~1 \le i \le n, 1 \le j \le m~ |
| 3 | 1250 | Không có ràng buộc gì thêm |
| Tổng | 2500 |
Sample Input 1
2 4
4 3 2 1
1 2 3 4
Sample Output 1
6
Sample Input 2
3 4
3 1 2 2
1 2 1 2
2 2 1 3
Sample Output 2
9
Sample Input 3
4 3
3 1 2
1 2 2
2 1 1
2 2 3
Sample Output 3
10
Notes
Ở ví dụ đầu tiên, tất cả các hình chữ nhật con đều có bốn góc thỏa mãn điều chặt cây ở đề bài.
Ở ví dụ thứ hai, ngoài ~6~ hình chữ nhật con có kích thước ~2 \times 2~ thì còn ~3~ cách chọn bộ bốn cây như sau:
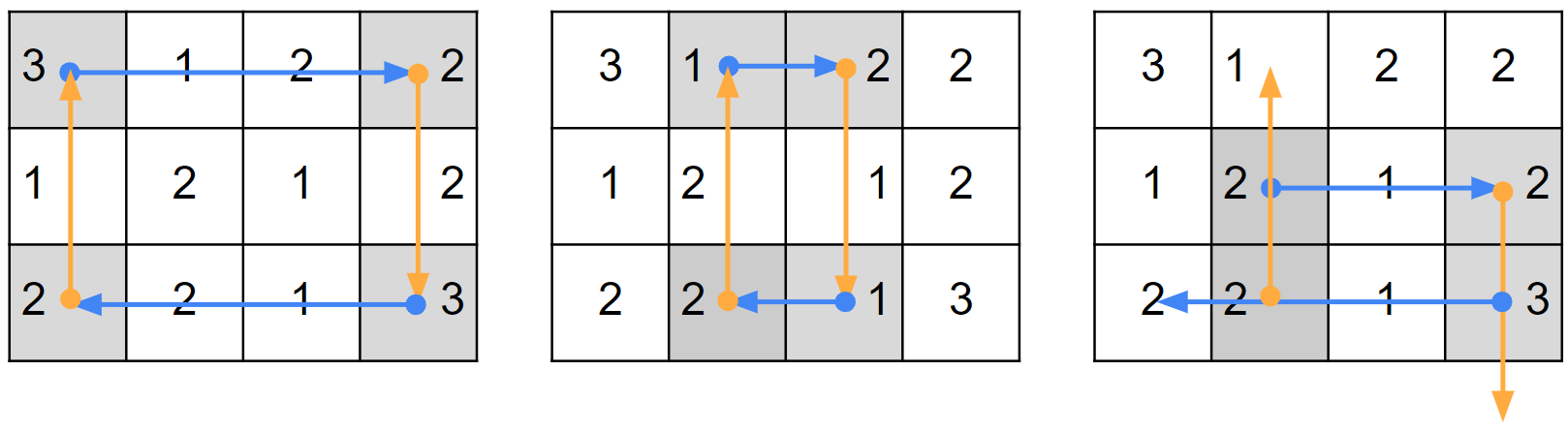
Hình vẽ minh họa ví dụ thứ hai.
Bình luận
Bình luận này đã bị ẩn vì có quá nhiều phản ứng tiêu cực. Nhấn để xem.