Quân tượng
Xem dạng PDFNhanh nhạy khi tấn công và phòng thủ tầm xa, mang trong mình phong thái của một nhà hoạch định chiến lược, đặc biệt phát huy năng lực khi thế trận thông thoáng, đó là tất cả những đặc điểm của một quân nhẹ chủ lực trên bàn cờ vua — quân tượng.
Với các đặc điểm tuyệt vời trên, việc khéo léo để sử dụng quân tượng trong mỗi ván cờ là hết sức quan trọng. Để tập luyện, Trung đã đầu tư mua về hẳn một bàn cờ vua kích thước ~n~ ~\times~ ~m~ chỉ để học cách sử dụng các quân tượng. Cậu đã đặt trước ~k~ quân tượng trên bàn cờ, quân thứ ~i~ được đặt ở ô có vị trí (~x_i~, ~y_i~) và muốn đặt thêm nhiều quân tượng vào bàn cờ nhất, sao cho không tồn tại hai quân nào có thể ăn nhau. Hai quân tượng chỉ có thể ăn nhau khi chúng nằm trên cùng một đường chéo.
Vì số lượng cách đặt có thể rất lớn, Trung lại muốn thử hết tất cả các cách để rút ra nhiều kinh nghiệm cho bản thân. Bạn hãy giúp Trung tính số lượng quân tượng nhiều nhất có thể đặt thêm vào bàn cờ và số cách để thực hiện điều đó, in ra phần dư của số cách sau khi chia cho ~10^9+7~.
Input
Dòng đầu tiên chứa ba số nguyên ~n~, ~m~ và ~k~ (~1 \leq n \leq 16, 1 \leq m \leq 100, 0 \leq k \leq 100~) — kích thước của bàn cờ vua và số quân tượng đã có sẵn trên bàn cờ.
Dòng thứ ~i~ trong ~k~ dòng tiếp theo chứa hai số nguyên ~x_i~, ~y_i~ (~1 \leq x_i \leq n~, ~1 \leq y_i \leq m~) — vị trí của quân tượng thứ ~i~.
Dữ liệu đảm bảo ~k~ quân tượng Trung đã đặt không tồn tại hai quân có thể ăn nhau.
Output
Một dòng duy nhất chứa hai số nguyên là số lượng quân tượng tối đa có thể đặt thêm và số cách để đặt thêm tối đa các con tượng modulo ~10^9 + 7~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | 500 | ~1 \leq n, m \leq 4~ |
| 2 | 750 | ~1 \leq n \leq 8, 1 \leq m \leq 100~ |
| 3 | 1500 | Không có ràng buộc gì thêm |
| Tổng | 2750 |
Sample Input 1
3 3 1
2 2
Sample Output 1
2 2
Sample Input 2
4 4 2
1 1
4 1
Sample Output 2
4 4
Sample Input 3
8 100 4
2 5
8 6
8 99
5 1
Sample Output 3
102 857399411
Notes
Các ô màu xanh chứa quân tượng màu đen là những quân tượng có sẵn trên bàn cờ. Những quân tượng màu trắng là những quân tượng được đặt thêm.
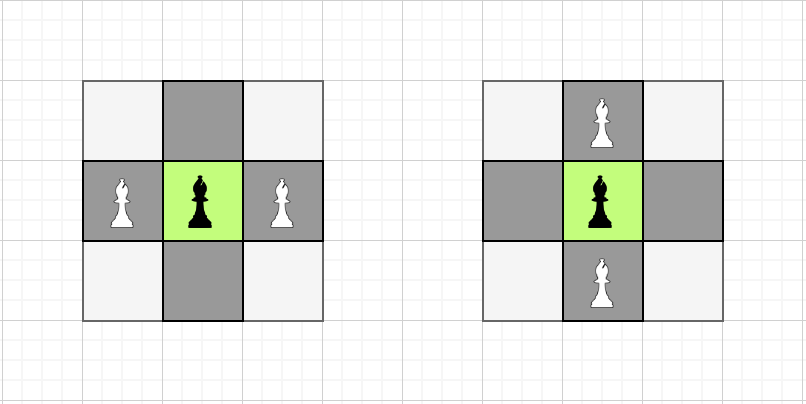
Minh họa cho ví dụ đầu tiên.
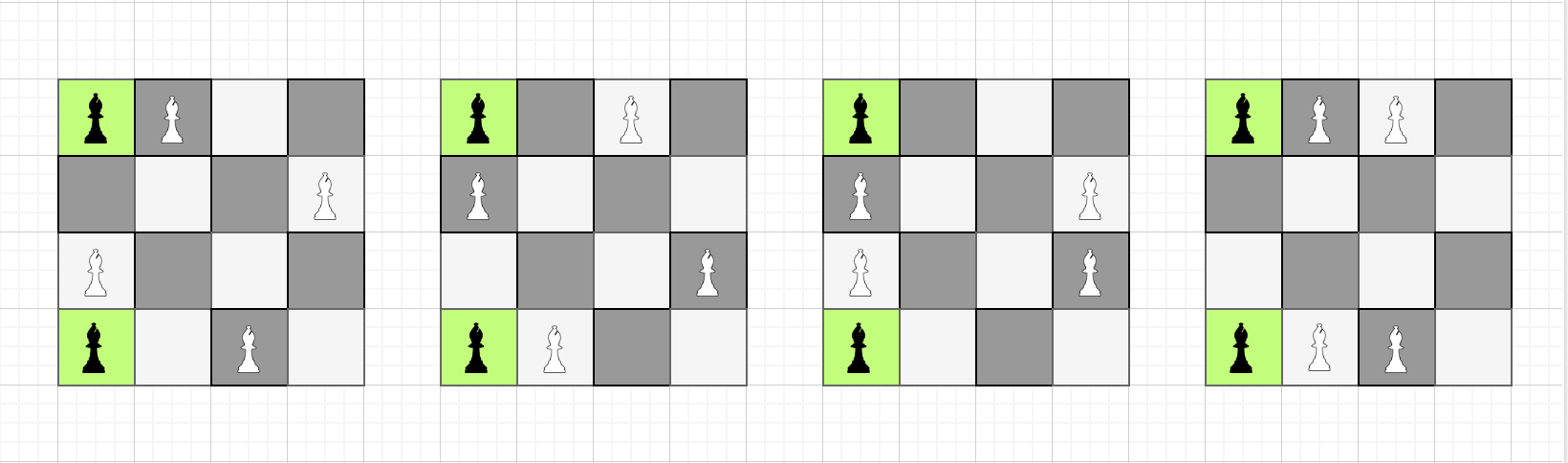
Minh họa cho ví dụ thứ hai
Bình luận