VNOI CUP 2023 - Vòng loại thứ nhất
Điểm: 500
MofK nuôi ~n~ con bò, và anh ấy rất quan tâm tới quan hệ tình cảm giữa
bọn chúng. Sau một thời gian quan sát, MofK nhận thấy mỗi con bò chỉ yêu
đúng một người bò khác: con bò thứ ~i~ đã đem lòng yêu thầm con bò
thứ ~p_i~ (~p_i \neq i~).
Là một người hâm mộ chân chính của thể loại truyện romcom, MofK không thể bỏ qua cơ hội này. Anh ấy muốn biết xem có ~3~ con bò nào tạo nên một mối tình tay ba hay không. Ba con bò phân biệt ~a~, ~b~, và ~c~ tạo nên mối tình tay ba nếu ~a~ yêu ~b~, ~b~ yêu ~c~, và ~c~ yêu ~a~.
Bạn hãy trả lời câu hỏi giúp MofK nhé!
Input
Mỗi input sẽ gồm nhiều test cases. Dòng đầu tiên của input gồm số nguyên dương ~t~ (~1 \le t \le 100~) — số test cases của bài toán. Sau đây là mô tả của các test cases.
Dòng đầu tiên của mỗi test case gồm số nguyên dương ~n~ (~3 \le n \le 100~) — số lượng con bò mà MofK nuôi.
Dòng tiếp theo của mỗi test case gồm ~n~ số nguyên ~p_1, p_2, \dots, p_n~ (~1 \le p_i \le n~, ~p_i \neq i~) — chỉ số của con bò khác mà mỗi con bò đang yêu.
Output
Với mỗi test case, in ra "<3" (không chứa ngoặc nháy) nếu tồn tại một mối tình tay ba giữa các con bò, ngược lại in "</3" (không chứa ngoặc nháy).
Scoring
Số điểm nhận được nếu bạn giải thành công bài toán này là ~500~ điểm.
Sample Input 1
2
5
4 1 5 2 2
4
2 3 4 1
Sample Output 1
<3
</3
Notes
Ở test case đầu tiên, ta có thể tìm được mối tình tay ba giữa ~3~ con bò ~[1, 2, 4]~ khi ~1~ yêu ~4~, ~4~ yêu ~2~ còn ~2~ lại yêu ~1~.
Ở test case thứ hai, mặc dù ~4~ con bò tạo ra một vòng tròn tình yêu nhưng lại không có mối tình tay ba nào cả (đây là tình tay bốn!)
Điểm: 1000
Lại một lần nữa, Megumin — phù thủy chuyên gia về pháp thuật explosion — lại bị thử thách bởi Yunyun — phù thủy chuyên gia về pháp thuật cao cấp, người tự xưng là đối thủ của Megumin. Như mọi lần, Megumin luôn là người chọn ra thử thách, và thử thách của Megumin lúc nào cũng quái đản.
Để chuẩn bị cho thử thách, mỗi cô phù thủy sẽ phù phép ra một con rùa và một con ốc sên. Mỗi con rùa sẽ có độ dài của mai là ~10\text{ cm}~. Mỗi con ốc sên có chiều dài không đáng kể, và có thể coi như là chất điểm. Sau khi phù phép ra, mỗi cô phù thủy sẽ đặt con ốc sên vào phần đuôi của mai con rùa của mình.

Thử thách mà Megumin đặt ra lần này là một cuộc đua. Chặng đua là một tuyến đường thẳng có chiều dài ~100\text{ cm}~. Hai cô phù thủy đặt chú rùa của mình vào vị trí xuất phát, sao cho hai chú rùa hướng về đích, và con ốc sên cách vạch đích ~100\text{ cm}~. Khi cuộc đua bắt đầu, hai con rùa sẽ di chuyển không ngừng theo một đường thẳng đến đích. Hai chú ốc sên cũng sẽ di chuyển trên mai rùa hướng đến đích, nhưng sẽ dừng lại khi đã đi hết chiều dài mai rùa. Người thắng cuộc trong cuộc đua này là người có con ốc sên cán vạch đích ở mốc ~100\text{ cm}~ trước.
Megumin đã phù phép ra con rùa và con ốc sên với vận tốc di chuyển lần lượt là ~t_m~ (cm/phút) và ~s_m~ (cm/phút). Còn vận tốc di chuyển của con rùa và con ốc sên mà Yunyun phù phép ra lần lượt là ~t_y~ (cm/phút) và ~s_y~ (cm/phút). Hãy tìm ra người thắng cuộc trong cuộc đua này.
Input
Dòng đầu tiên gồm số nguyên ~t~ (~1 \le t \le 10\,000~) — số lượng test case. Mỗi test case sẽ có mô tả như sau.
Mỗi test case gồm một dòng duy nhất gồm ~4~ số nguyên dương ~t_m~, ~s_m~, ~t_y~ và ~s_y~ (~1 \le t_m, s_m, t_y, s_y \le 100~) — tốc độ di chuyển của con rùa và ốc sên của Megumin và tốc độ di chuyển của con rùa và ốc sên của Yunyun.
Output
Mỗi test case cần in ra:
"Yunyun" (không chứa ngoặc nháy) nếu Yunyun là người chiến thắng cuộc đua.
"Megumin" (không chúa ngoặc nháy) nếu Megumin là người chiến thắng cuộc đua.
"Draw" (không chứa ngoặc nháy) nếu hai chú ốc sên của hai cô phù thủy cán đích cùng lúc.
Scoring
Số điểm nhận được nếu bạn giải thành công bài toán này là ~1000~ điểm.
Sample Input 1
7
30 2 29 1
30 1 29 2
29 3 30 1
21 3 20 5
45 5 45 10
21 3 20 5
3 1 3 7
Sample Output 1
Megumin
Draw
Megumin
Megumin
Draw
Megumin
Draw
Notes
Ví dụ đầu tiên đã được minh họa ở đề bài.
Ví dụ thứ hai có ~tm=30~, ~sm=1~, ~ty=29~, ~sy=2~. Trong ví dụ này, hai con ốc sên cán đích cùng lúc, do đó ta có kết quả là hòa nhau.

Minh họa cho ví dụ thứ hai
Ví dụ thứ ba có ~tm=29~, ~sm=3~, ~ty=30~, ~sy=1~. Trong ví dụ này, tuy Megumin có con rùa chậm hơn, nhưng con ốc sên của Megumin chạy nhanh hơn hẳn, do đó Megumin chiến thắng cuộc đua này.
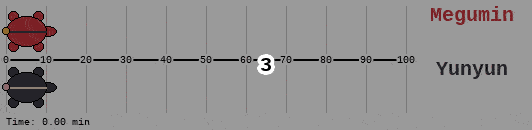
Minh họa cho ví dụ thứ ba
Alob và Bice là những người chơi đá giỏi nhất thế giới! Anh hùng thì trọng anh hùng, nhân dịp VNOI Cup, Alob và Bice đã hẹn gặp nhau ở vịnh Hạ Long để đàm đạo về đá học (stone-graphy).
Alob và Bice mỗi người sở hữu ~n~ viên đá, trên mỗi viên đá được viết một con số. Hai người sẽ xếp những viên đá của mình thành một dãy, với ~a_i~ là con số viết trên hòn đá thứ ~i~ của Alob, và ~b_j~ là con số viết trên hòn đá thứ ~j~ của Bice. Ta định nghĩa độ high của một cách sắp xếp là ~\sum \limits_{i = 1}^n \max(a_i, b_i)~.
Alob và Bice thống nhất rằng, họ muốn sắp xếp lại những viên đá của mình sao cho độ high đạt giá trị lớn nhất. Các bạn hãy giúp Alob và Bice nhé!
Input
Mỗi input sẽ gồm nhiều test cases. Dòng đầu tiên của input gồm số nguyên dương ~t~ (~1 \le t \le 10^3~) — số test cases của bài toán. Sau đây là mô tả của các test cases.
Dòng đầu tiên của mỗi test case gồm số nguyên dương ~n~ (~1 \le n \le 10^5~) — số viên đá mà Alob và Bice sở hữu.
Dòng thứ hai của mỗi test case gồm ~n~ số nguyên dương ~a_1, a_2, \ldots, a_n~ (~1 \le a_i \le 10^9~) — những con số viết trên những viên đá của Alob.
Dòng thứ ba của mỗi test case gồm ~n~ số nguyên dương ~b_1, b_2, \ldots, b_n~ (~1 \le b_i \le 10^9~) — những con số viết trên những viên đá của Bice.
Dữ liệu đảm bảo tổng của ~n~ trong tất cả các test cases không vượt quá ~10^5~.
Output
Với mỗi test case, in ra một số nguyên duy nhất — độ high lớn nhất có thể của một cách sắp xếp các viên đá.
Scoring
Số điểm nhận được nếu bạn giải thành công bài toán này là ~1000~ điểm.
Sample Input 1
2
3
1 4 3
3 5 2
2
4 5
7 9
Sample Output 1
12
16
Notes
Ở test case đầu tiên, ta có thể sắp xếp lại những viên đá của Alob thành ~[3, 1, 4]~, và sắp xếp lại những viên đá của Bice thành ~[3, 5, 2]~, khi đó độ high của cách sắp xếp này sẽ là ~\max(3, 3) + \max(1, 5) + \max(4, 2) = 3 + 5 + 4 = 12~.
Ở test case thứ hai, ta có thể sắp xếp lại những viên đá của Alob thành ~[5, 4]~, và sắp xếp lại những viên đá của Bice thành ~[9, 7]~, khi đó độ high của cách sắp xếp này sẽ là ~\max(5, 9) + \max(4, 7) = 9 + 7 = 16~.
Điểm: 2000
Nhân dịp sinh nhật, Tahp mua tặng bé Trung một bộ đồ chơi sắp xếp xâu và đố Trung giải được, nếu thành công sẽ dẫn Trung đi uống tà tưa. Bộ đồ chơi có một xâu ~s~ gồm ~n~ chữ cái tiếng Anh in thường. Mục tiêu của trò chơi là tìm cách sắp xếp các kí tự của xâu ~s~ sao cho cuối cùng thu được xâu ~t~.
Không được thông minh cho lắm, vì vậy Trung quyết định chơi ăn gian. Tại mỗi lượt, cậu sẽ chọn một đoạn các kí tự từ ~l~ đến ~r~ trên xâu ~s~, sau đó tháo các kí tự trong đoạn này ra và lắp lại theo ý thích của mình. Với mỗi vị trí ~i~ trên xâu ~s~, để tháo và lắp kí tự ở vị trí này tốn lượng thời gian ~a_i~ giây. Giá trị ~a_i~ chỉ tương ứng với vị trí ~i~, và không thay đổi sau khi ta đã xáo trộn các kí tự.
Ngoài ra, Trung không muốn tháo ra lắp vào bộ đồ chơi quá ~k~ lượt vì sợ làm hỏng nó. Hãy tính thời gian nhỏ nhất Trung cần bỏ ra để hoàn thành trò chơi này.
Input
Dòng đầu tiên gồm hai số nguyên dương ~n~ và ~k~ (~1 \le n \le 10^5~, ~1 \le k \le 10^5~) — lần lượt là độ dài của hai xâu kí tự, và số lần lắp ráp tối đa mà Trung có thể thực hiện.
Dòng thứ hai gồm một xâu ~s~ độ dài ~n~ chứa các chữ cái tiếng Anh in thường — xâu ban đầu trong bộ đồ chơi.
Dòng thứ ba gồm một xâu ~t~ độ dài ~n~ chứa các chữ cái tiếng Anh in thường — xâu mục tiêu mà bé Trung muốn đạt được.
Dòng cuối cùng gồm ~n~ số nguyên dương ~a_1, a_2, \ldots, a_n~ (~1 \leq a_i \leq 10^9~) — thời gian cần thiết để tháo ra và lắp vào của các vị trí trên xâu ~s~.
Dữ liệu đảm bảo luôn tồn tại cách để đưa xâu ~s~ về giống xâu ~t~.
Output
Một số nguyên duy nhất là thời gian tối thiểu Trung cần bỏ ra.
Scoring
Subtask 1 (~750~ điểm): ~n, k \leq 100~.
Subtask 2 (~500~ điểm): ~n \leq 10^5, k \leq 100~.
Subtask 3 (~750~ điểm): không có ràng buộc gì thêm.
Tổng số điểm nhận được nếu bạn giải thành công bài toán này là ~2000~ điểm.
Sample Input 1
9 2
abcabcbab
bacacbbba
1 2 4 6 2 1 7 3 2
Sample Output 1
18
Sample Input 2
8 1
tahpnaot
toanphat
5 7 3 2 8 5 2 4
Sample Output 2
27
Notes
Trong ví dụ đầu tiên:
Lần thứ nhất, Trung chọn đoạn ~[1, 2]~ và tạo ra xâu bacabcbab, tốn ~3~ giây.
Lần thứ hai, Trung chọn đoạn ~[5, 9]~ và tạo ra xâu bacacbbba, tốn ~15~ giây.
Trong ví dụ thứ hai:
- Trung chọn đoạn ~[2, 7]~ và tạo ra xâu toanphat, tốn ~27~ giây.
Thành phố Trung sinh sống có thể được biểu diễn trên mặt phẳng tọa độ. Toàn bộ thành phố là một hình vuông có cạnh song song với trục tọa độ, được giới hạn bởi hai điểm ~(0, 0)~ và ~(n, n)~. Hiện tại nơi đây đang bị các phần tử khủng bố tấn công. Chúng đã đặt ~m~ quả bom khắp thành phố, quả bom thứ ~i~ được đặt ở vị trí có tọa độ ~(x_i, y_i)~.
Mỗi quả bom đều có sức công phá ~l~, khi một quả bom ở vị trí ~(x, y)~ phát nổ, tất cả những địa điểm có tọa độ ~(p, q)~ trong thành phố thỏa mãn ~x - l \le p \le x + l~ và ~y - l \le q \le y + l~ sẽ bị phá hủy. Nếu tại địa điểm ~(p, q)~ bị phá hủy tồn tại một quả bom khác, quả bom đó cũng sẽ phát nổ.
Đám khủng bố dự định sẽ kích nổ một quả bom bất kì để hăm dọa người dân. Hiện tại vị trí Trung đang làm việc có tọa độ ~(0, 0)~, vị trí nhà của cậu có tọa độ ~(n, n)~. Từ vị trí có tọa độ ~(x, y)~, Trung chỉ có thể đi sang ~4~ vị trí ~(x- 1, y)~, ~(x, y-1)~, ~(x+1, y)~, ~(x, y+1)~ và không được đi ra khỏi thành phố. Trung lo lắng rằng việc kích nổ một quả bom có thể khiến đường về nhà của cậu bị chặn. Hãy giúp Trung tính xem những quả bom nào sau khi kích nổ có thể khiến Trung không thể về nhà được nữa để cậu nhanh chóng tìm chỗ trú ẩn an toàn.
Input
Dòng đầu tiên gồm ba số nguyên dương ~n~, ~m~, ~l~ (~1 \leq n \leq 10^9~, ~1 \leq m \leq 2 \cdot 10^5~, ~0 \leq l \leq 10^9~) — lần lượt là kích thước thành phố Trung sống, số quả bom và sức công phá của mỗi quả bom.
Dòng thứ ~i~ trong ~m~ dòng tiếp theo gồm hai số nguyên ~x_i~ và ~y_i~ (~0 \leq x_i, y_i \leq n~) — tọa độ của quả bom thứ ~i~. Dữ liệu đảm bảo rằng không có hai quả bom nào được đặt ở cùng vị trí và có thể tồn tại quả bom nổ nhà hoặc công ty.
Output
Dòng đầu tiên gồm số nguyên ~k~ là số quả bom khi bị kích nổ sẽ khiến Trung không thể về nhà.
Dòng thứ ~i~ trong ~k~ dòng tiếp theo gồm hai số nguyên ~x_i~ và ~y_i~ mô tả tọa độ của quả bom. Các quả bom có thể in ra theo thứ tự bất kì.
Scoring
Subtask 1 (~750~ điểm): ~n, m \leq 100~.
Subtask 2 (~500~ điểm): ~m \leq 2000~.
Subtask 3 (~1250~ điểm): không có ràng buộc gì thêm.
Tổng số điểm nhận được nếu bạn giải thành công bài toán này là ~2500~ điểm.
Sample Input 1
4 2 2
1 3
3 1
Sample Output 1
2
1 3
3 1
Sample Input 2
2 1 1
1 1
Sample Output 2
1
1 1
Notes
Ở ví dụ đầu tiên có hai quả bom. Có thể thấy rằng khi kích hoạt một quả bom thì quả bom còn lại cũng bị phát nổ. Cả hai quả bom khi phát nổ sẽ chặn hết mọi con đường về nhà của Trung.
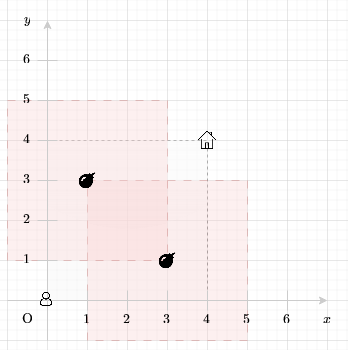
Minh họa cho ví dụ đầu tiên. Phần màu đỏ thể hiện nhưng vị trí bị phá hủy khi bom phát nổ.
Ở ví dụ thứ hai có duy nhất một quả bom, tuy nhiên khi quả bom này phát nổ, toàn bộ vị trí trong thành phố đều bị phá hủy.
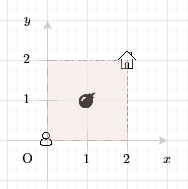
Minh họa cho ví dụ thứ hai
Điểm: 3000
Nhận thấy thị trường mua bán dế mèn đang nhộn nhịp, nhiều người đã đổi đời nhờ việc nuôi và mua bán dế, Tahp quyết định dấn thân vào để kiếm lời.
Tahp đã đầu tư một chuồng dế với sức chứa ~l~ con và muốn dùng nó để giàu lên. Tahp dự định sẽ đầu tư trong ~n~ ngày. Ban đầu Tahp không nuôi con dế nào, và đến cuối ngày ~n~ Tahp cũng muốn mình không còn nuôi bất kì con dế nào để tập trung đầu tư vào lĩnh vực khác. Trong ~n~ ngày tiếp theo, Tahp sẽ ra chợ để giao dịch dế.
Vào ngày thứ ~i~, ở chợ có sẵn ~a_i~ con dế được bày bán với giá ~s_i~ đồng mỗi con. Đồng thời, chợ cũng thu mua dế với giá ~b_i~ đồng mỗi con và chỉ thu mua tối đa ~c_i~ con. Tahp có thể chọn mua thêm hoặc bán bớt dế đang nuôi, hoặc không làm gì cả. Tuy nhiên, cuối mỗi ngày, với mỗi con dế đang nuôi, Tahp cần tốn thêm ~k~ đồng để mua thức ăn cho nó. Ngoài ra, với tất cả các ngày, ~b_i \le s_i~.
Giả sử Tahp luôn có đủ tiền để mua thêm dế và mua thức ăn, hãy giúp Tahp tính toán lợi nhuận tối đa có thể sau ~n~ ngày.
Input
Mỗi test có thể chứa nhiều bộ dữ liệu. Dòng đầu tiên chứa số nguyên ~t~ (~1 \le t \le 100~) — số bộ dữ liệu, theo sau đó là ~t~ nhóm dòng có cấu trúc như nhau:
Dòng đầu tiên chứa ba số nguyên ~n~, ~l~, ~k~ (~1 \le n \le 10^5~, ~1 \le l \le 10^{12}~, ~1 \le k \le 2 \cdot 10^6~) — lần lượt là số ngày Tahp muốn đầu tư, sức chứa của lồng dế và tiền mua thức ăn hàng ngày cho mỗi con dế;
Dòng thứ ~i~ trong ~n~ dòng tiếp theo chứa ba số nguyên ~a_i~, ~s_i~, ~c_i~, ~b_i~ (~1 \le a_i, s_i, c_i, b_i \le 2 \cdot 10^6~; ~b_i \le s_i~) — lần lượt là số lượng dế được bày bán, giá bán ra mỗi con dế, giới hạn số lượng dế thu mua và giá mua vào mỗi con dế ở chợ vào ngày thứ ~i~.
Hai số liên tiếp trên một dòng cách nhau bởi dấu cách. Dữ liệu đảm bảo tổng ~n~ trong tất cả các bộ dữ liệu không vượt quá ~5 \cdot 10^5~.
Output
Với mỗi bộ dữ liệu, in ra tổng lợi nhuận lớn nhất trên một dòng.
Scoring
Subtask 1 (~750~ điểm): ~l \le 10~.
Subtask 2 (~1500~ điểm): ~l = 10^{12}~.
Subtask 3 (~750~ điểm): không có giới hạn gì thêm.
Tổng số điểm nhận được nếu bạn giải thành công bài toán này là ~3000~ điểm.
Sample Input 1
2
3 4 1
2 4 2 1
3 5 1 4
1 10 3 9
2 7 2
8 7 10 1
3 9 3 8
Sample Output 1
9
0
Notes
Ở bộ dữ liệu đầu tiên, Tahp đầu tư trong ~n = 3~ ngày, chuồng dế có sức chứa ~l = 4~ con và tiền mua thức ăn hàng ngày cho mỗi con dế là ~k = 1~ đồng. Một cách để đạt lợi nhuận tối đa là:
Ở ngày thứ nhất, chợ có ~a_1 = 2~ con dế được bày bán với giá ~s_1 = 4~ đồng mỗi con, và thu mua tối đa ~c_1 = 2~ con dế với giá ~b_1 = 1~ đồng mỗi con. Tahp mua thêm ~2~ con dế với giá ~2 \times 4 = 8~ đồng. Cuối ngày, Tahp đang nuôi tổng cộng ~2~ con dế và cần mua thức ăn hết ~2 \times 1 = 2~ đồng.
Ở ngày thứ hai, chợ có ~a_2 = 3~ con dế được bày bán với giá ~s_2 = 5~ đồng mỗi con, và thu mua tối đa ~c_2 = 1~ con dế với giá ~b_2 = 4~ đồng mỗi con. Tahp mua thêm ~1~ con dế nữa với giá ~1 \times 5 = 5~ đồng. Cuối ngày, Tahp đang nuôi tổng cộng ~3~ con dế và cần mua thức ăn hết ~3 \times 1 = 3~ đồng.
Ở ngày thứ ba, chợ có ~a_3 = 1~ con dế được bày bán với giá ~s_2 = 10~ đồng mỗi con, và thu mua tối đa ~c_3 = 3~ con dế với giá ~b_3 = 9~ đồng mỗi con. Tahp bán đi ~3~ con dế đang nuôi với giá ~3 \times 9 = 27~ đồng. Cuối ngày, Tahp đang không nuôi con dế nào nên không phải trả tiền thức ăn.
Tổng lợi nhuận thu được: ~(-8) + (-2) + (-5) + (-3) + 27 = 9~ đồng.