Khủng bố
Xem dạng PDFThành phố Trung sinh sống có thể được biểu diễn trên mặt phẳng tọa độ. Toàn bộ thành phố là một hình vuông có cạnh song song với trục tọa độ, được giới hạn bởi hai điểm ~(0, 0)~ và ~(n, n)~. Hiện tại nơi đây đang bị các phần tử khủng bố tấn công. Chúng đã đặt ~m~ quả bom khắp thành phố, quả bom thứ ~i~ được đặt ở vị trí có tọa độ ~(x_i, y_i)~.
Mỗi quả bom đều có sức công phá ~l~, khi một quả bom ở vị trí ~(x, y)~ phát nổ, tất cả những địa điểm có tọa độ ~(p, q)~ trong thành phố thỏa mãn ~x - l \le p \le x + l~ và ~y - l \le q \le y + l~ sẽ bị phá hủy. Nếu tại địa điểm ~(p, q)~ bị phá hủy tồn tại một quả bom khác, quả bom đó cũng sẽ phát nổ.
Đám khủng bố dự định sẽ kích nổ một quả bom bất kì để hăm dọa người dân. Hiện tại vị trí Trung đang làm việc có tọa độ ~(0, 0)~, vị trí nhà của cậu có tọa độ ~(n, n)~. Từ vị trí có tọa độ ~(x, y)~, Trung chỉ có thể đi sang ~4~ vị trí ~(x- 1, y)~, ~(x, y-1)~, ~(x+1, y)~, ~(x, y+1)~ và không được đi ra khỏi thành phố. Trung lo lắng rằng việc kích nổ một quả bom có thể khiến đường về nhà của cậu bị chặn. Hãy giúp Trung tính xem những quả bom nào sau khi kích nổ có thể khiến Trung không thể về nhà được nữa để cậu nhanh chóng tìm chỗ trú ẩn an toàn.
Input
Dòng đầu tiên gồm ba số nguyên dương ~n~, ~m~, ~l~ (~1 \leq n \leq 10^9~, ~1 \leq m \leq 2 \cdot 10^5~, ~0 \leq l \leq 10^9~) — lần lượt là kích thước thành phố Trung sống, số quả bom và sức công phá của mỗi quả bom.
Dòng thứ ~i~ trong ~m~ dòng tiếp theo gồm hai số nguyên ~x_i~ và ~y_i~ (~0 \leq x_i, y_i \leq n~) — tọa độ của quả bom thứ ~i~. Dữ liệu đảm bảo rằng không có hai quả bom nào được đặt ở cùng vị trí và có thể tồn tại quả bom nổ nhà hoặc công ty.
Output
Dòng đầu tiên gồm số nguyên ~k~ là số quả bom khi bị kích nổ sẽ khiến Trung không thể về nhà.
Dòng thứ ~i~ trong ~k~ dòng tiếp theo gồm hai số nguyên ~x_i~ và ~y_i~ mô tả tọa độ của quả bom. Các quả bom có thể in ra theo thứ tự bất kì.
Scoring
Subtask 1 (~750~ điểm): ~n, m \leq 100~.
Subtask 2 (~500~ điểm): ~m \leq 2000~.
Subtask 3 (~1250~ điểm): không có ràng buộc gì thêm.
Tổng số điểm nhận được nếu bạn giải thành công bài toán này là ~2500~ điểm.
Sample Input 1
4 2 2
1 3
3 1
Sample Output 1
2
1 3
3 1
Sample Input 2
2 1 1
1 1
Sample Output 2
1
1 1
Notes
Ở ví dụ đầu tiên có hai quả bom. Có thể thấy rằng khi kích hoạt một quả bom thì quả bom còn lại cũng bị phát nổ. Cả hai quả bom khi phát nổ sẽ chặn hết mọi con đường về nhà của Trung.
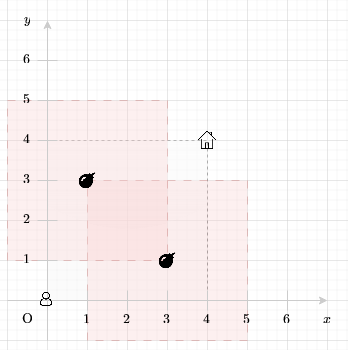
Minh họa cho ví dụ đầu tiên. Phần màu đỏ thể hiện nhưng vị trí bị phá hủy khi bom phát nổ.
Ở ví dụ thứ hai có duy nhất một quả bom, tuy nhiên khi quả bom này phát nổ, toàn bộ vị trí trong thành phố đều bị phá hủy.
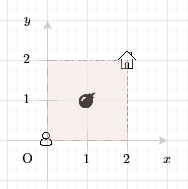
Minh họa cho ví dụ thứ hai
Bình luận