Educational Euler Tour and HLD Contest
Điểm: 100
Bạn được cho ~1~ cái cây gồm ~n~ đỉnh, với đỉnh ~1~ là nút gốc, và giá trị tương ứng của từng đỉnh.
Nhiệm vụ của bạn là cần phải thực hiện ~q~ truy vấn có dạng như sau:
~1~. Đổi giá trị của nút ~s~ thành ~x~.
~2~. Tính tổng giá trị của các nút nằm trong cây con gốc ~s~.
Input
Dòng đầu gồm ~2~ số ~n~ và ~q~ (~1 \leq n, q \leq 2 \times 10^5~) tương ứng là số lượng nút trong cây và truy vấn.
Dòng tiếp theo là dãy ~n~ số ~a_1, a_2, a_3, \cdots, a_n~ (~1 \leq a_i \leq 10^9~) là giá trị ban đầu của nút tương ứng trên cây.
Tiếp theo là ~n - 1~ cặp số ~a~, ~b~ (~1 \leq a, b \leq n~) cho ta biết cạnh giữa ~2~ nút ~a - b~ trên cây.
Trong ~q~ dòng cuối cùng là các truy vấn có ~1~ trong ~2~ dạng:
— ~1~ ~s~ ~x~ (~1 \leq s \leq n~, ~1 \leq x \leq 10^9~).
— ~2~ ~s~ (~1 \leq s \leq n~).
Output
Xuất ra từng dòng tương ứng đáp án của từng truy vấn loại ~2~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~50\%~ | ~n \le 5000, q \le 5000~. |
| 2 | ~50\%~ | Không có ràng buộc gì thêm. |
Sample Input 1
5 3
4 2 5 2 1
3 5
1 3
2 1
3 4
2 3
1 5 3
2 3
Sample Output 1
8
10
Sample Input 2
10 10
2 9 19 10 2 3 2 1 9 8
7 2
9 5
3 7
1 8
1 6
8 5
8 10
1 4
3 8
2 3
2 8
1 3 1
2 1
2 10
1 10 2
2 3
1 3 3
2 6
2 2
Sample Output 2
30
50
47
8
12
3
9
Notes
Trong test ví dụ đầu tiên, hình ảnh của cây ban đầu:
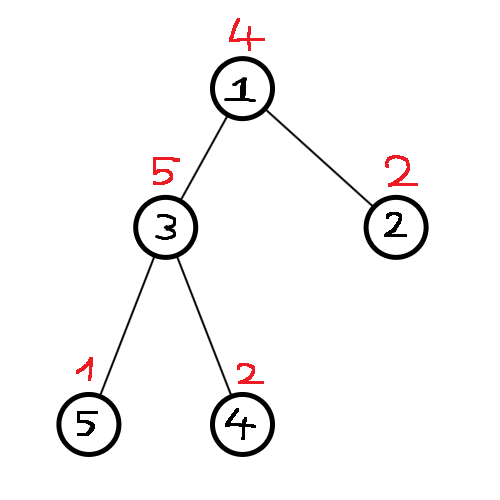
Truy vấn "~2~ ~3~" sẽ lấy tổng phần khoanh vùng:
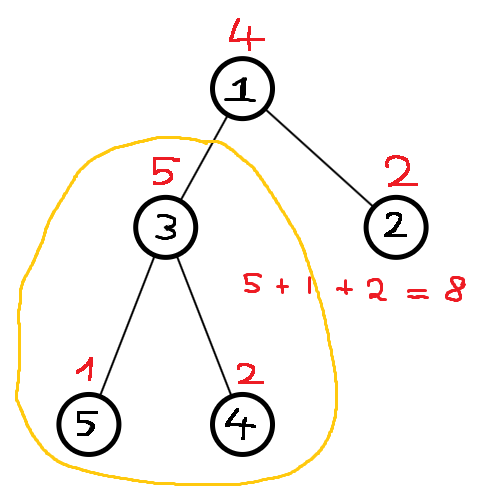
cho ra đáp án là: ~8~.
Sau truy vấn "~1~ ~5~ ~3~", đổi giá trị ở nút ~5~ thành ~3~:
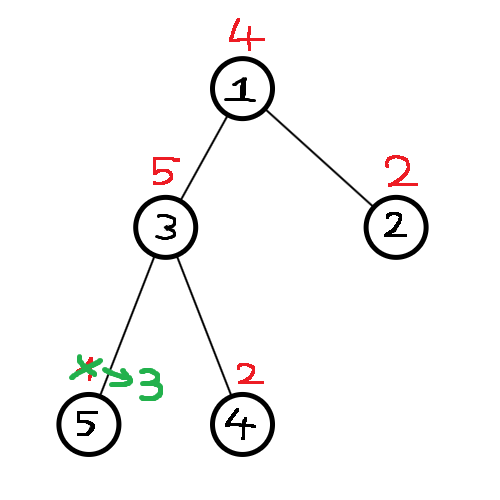
Cuối cùng, truy vấn "~2~ ~3~" sẽ lấy tổng phần khoanh vùng:
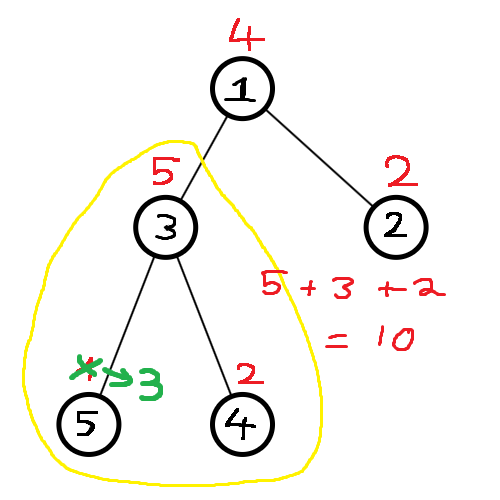
cho ra đáp án là: ~10~.
Điểm: 100
Cho một cây có gốc bao gồm ~n~ nút. Các nút được đánh số ~1, 2, ..., n~ và nút ~1~ là gốc của cây. Mỗi nút có một giá trị.
Nhiệm vụ của bạn là xử lý các loại truy vấn sau:
~1~. Thay đổi giá trị của nút ~s~ thành ~x~.
~2~. Tính tổng giá trị trên đường đi từ gốc cây tới nút ~s~.
Input
Dòng đầu vào đầu tiên chứa hai số nguyên ~n~ và ~q~ ~(1 \le n, q \le 2 \cdot 10^5)~ là số lượng nút và truy vấn. Các nút được đánh số ~1, 2, ..., n~.
Dòng tiếp theo chứa ~n~ số nguyên ~v_1, v_2, ..., v_n~ ~(1 \le v_i \le 10^9)~ lần lượt là giá trị của mỗi nút.
Sau đó, có ~n - 1~ dòng mô tả các cạnh. Mỗi dòng chứa hai số nguyên ~a~ và ~b~ ~(1 \le a, b \le n)~ : có một cạnh nối giữa hai nút ~a~ và ~b~.
Cuối cùng, có ~q~ dòng mô tả các truy vấn. Mỗi truy vấn có dạng "1 ~s~ ~x~" hoặc "2 ~s~" ~(1 \le s \le n, 1 \le x \le 10^9~).
Output
- In câu trả lời cho mỗi truy vấn loại ~2~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~30~ | ~n, q \le 1000~ |
| 2 | ~70~ | Không ràng buộc gì thêm. |
Sample Input 1
5 3
4 2 5 2 1
1 2
1 3
3 4
3 5
2 4
1 3 2
2 4
Sample Output 1
11
8
Điểm: 100
Bananabread và Tutel Master đang đi chơi arcade ở địa điểm N giấu tên. Ở đây, Tutel Master đã gặp một trò khá thú vị. Đầu tiên, máy sẽ cho Tutel Master một bản đồ được biểu diễn bằng ~N~ căn phòng có thể có kho báu được nối với nhau bởi ~N-1~ lối đi với lối đi thứ ~i~ có độ dài là ~w_i~ liên thông với nhau. Nghĩa là, luôn có duy nhất một đường đi từ mọi cặp căn phòng.
Máy cho bạn biết là vòng này máy sẽ làm ~Q~ hành động. Mỗi lượt, máy sẽ lựa chọn, thông báo cho Tutel Master và làm một trong hai hành động:
~1~ ~i~ ~w~: máy sẽ sử dụng ma thuật để mà biến độ dài lối đi thứ ~i~ thành độ dài ~w~ mới. Con đường thứ ~i~ sẽ có độ dài ~w~ này cho đến khi được biến đổi lại.
~2~ ~a~ ~b~: máy sẽ đặt bạn vào phòng thứ ~a~ và bạn phải tìm tổng độ dài phải đi để đến phòng thứ ~b~ để lấy kho báu. Tutel Master cần cho máy biết rằng tổng độ dài này.
Tutel Master chỉ có rất ít thời gian để trả lời hành động loại thứ hai. May rằng, Tutel Master biết là Bananabread có thể dễ dàng làm bài này. Vì Bananabread đang lo farm các trò khác nên đã nhờ bạn hỗ trợ Tutel Master. Bạn hãy giúp Tutel Master nhé.
Input
Dòng đầu gồm một số nguyên dương ~N~ ~(1\le N \le 200000)~.
~N-1~ dòng tiếp theo, dòng thứ ~i~ gồm ba số là ~a_i,b_i,w_i~ là có cạnh giữa đỉnh ~a_i~ và ~b_i~ với độ dài là ~w_i~. ~(1\le a_i,b_i \le N,1\le w_i\le 10^9)~
Dòng tiếp theo có một số nguyên dương ~Q~ ~(1\le Q \le 200000)~.
~Q~ dòng tiếp theo, mỗi dòng gồm ba số có dạng là ~1~ ~i~ ~w~ hoặc ~2~ ~a~ ~b~.
Output
- Gồm một số dòng là đáp án của các truy vấn loại ~2~
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~50\%~ | ~1\le N,Q \le 5000~ |
| 2 | ~50\%~ | Không có ràng buộc gì thêm |
Sample Input 1
5
1 2 3
1 3 6
1 4 9
4 5 10
4
2 2 3
2 1 5
1 3 1
2 1 5
Sample Output 1
9
19
11
Sample Input 2
7
1 2 1000000000
2 3 1000000000
3 4 1000000000
4 5 1000000000
5 6 1000000000
6 7 1000000000
3
2 1 6
1 1 294967296
2 1 6
Sample Output 2
5000000000
4294967296
Sample Input 3
1
1
2 1 1
Sample Output 3
0
Sample Input 4
8
1 2 105
1 3 103
2 4 105
2 5 100
5 6 101
3 7 106
3 8 100
18
2 2 8
2 3 6
1 4 108
2 3 4
2 3 5
2 5 5
2 3 1
2 4 3
1 1 107
2 3 1
2 7 6
2 3 8
2 1 5
2 7 6
2 4 7
2 1 7
2 5 3
2 8 6
Sample Output 4
308
409
313
316
0
103
313
103
525
100
215
525
421
209
318
519
Notes
Giải thích test ví dụ 1:
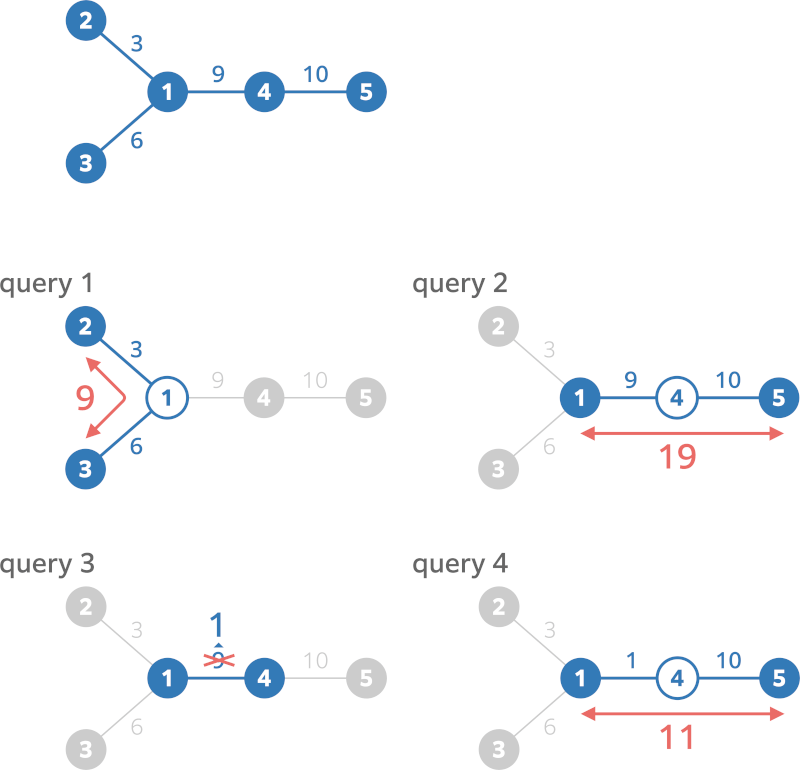
Điểm: 100
Cho một cây gồm ~n~ đỉnh có gốc tại đỉnh ~1~. Đỉnh thứ ~i~ (~1 \leq i \leq n~) được gán màu sắc là ~c_i~.
Với mỗi đỉnh ~i~, xác định số màu sắc phân biệt có trong cây con gốc ~i~.
Input
Dòng đầu chứa số nguyên dương ~n~ (~1 \leq n \leq 2 \times 10^5~).
Dòng thứ hai chứa ~n~ số nguyên dương cách nhau bởi dấu cách biểu diễn mảng ~c~, với ~c_i~ là màu sắc của đỉnh thứ ~i~ (~1 \leq c_i \leq 10^9~).
~n-1~ dòng tiếp theo, mỗi dòng chứa hai số nguyên ~a, b~ biểu diễn một cạnh hai chiều giữa đỉnh ~a~ và ~b~ (~1 \leq a,b \leq n~).
Output
Gồm một dòng duy nhất chứa ~n~ số nguyên cách nhau bởi dấu cách, số thứ ~i~ là số màu sắc phân biệt trong tất cả các đỉnh thuộc cây con gốc ~i~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | 40 | ~n \leq 5000~ |
| 2 | 60 | ~n \leq 2 \times 10^5~ |
Sample Input 1
5
2 3 2 2 1
1 2
1 3
3 4
3 5
Sample Output 1
3 1 2 1 1
Sample Input 2
4
1 1 3 1000
1 2
2 3
2 4
Sample Output 2
3 3 1 1
Notes
Trong test đầu tiên, cây con của đỉnh ~1~ bao gồm tất cả các đỉnh trong cây, mang ~3~ giá trị màu sắc khác nhau. Cây con của đỉnh ~3~ bao gồm ba đỉnh là ~3, 4, 5~ lần lượt mang các màu ~2, 2, 1~, có tất cả ~2~ màu sắc phân biệt là màu ~1~ và ~2~.
Trong test thứ hai, cây con của đỉnh ~1~ và đỉnh ~2~ đều có ~3~ màu sắc phân biệt là màu ~1, 3, 1000~.
Monkey D. Demen đang trên đường tiến vào Đại Hải trình cùng với băng hải tặc Dilengoo để đi tìm kho báu Two Piece. Trước khi vào Đại Hải trình, Demen đã vô tình giải cứu nhà thông thái Bedao khỏi băng hải tặc Dotree. Để cảm tạ ơn cứu mạng của Demen, Bedao đã tặng cho Demen báu vật quý giá nhất của mình là một tấm bản đồ gồm ~N~ hòn đảo thuộc Đại Hải trình được đánh số từ ~1, 2, ..., N~ với ~N-1~ tuyến đường bí mật giữa các hòn đảo và một tấm vé thông hành có thể đi từ hòn đảo Demen đang đứng tới một hòn đảo bất kì cách đó đúng ~K~ tuyến đường bí mật. Trước khi chia tay, Bedao đã hô biến Demen và băng hải tặc của cậu tới hòn đảo ~U~. Vì muốn nhanh chóng lấy được kho báu Two Piece, Demen đã quyết định sử dụng ngay tấm vé thông hành có mã số ~K~ của Bedao, nhưng cậu không biết hòn đảo nào đang cách cậu đúng ~K~ tuyến đường bí mật cả. Sau một hồi ngẫm nghĩ, nhớ ra bạn là một người rất rành về bản đồ và đường đi, Demen đã sử dụng Ốc sên truyền tin để liên lạc với bạn để tìm sự giúp đỡ.
Bằng tài năng của mình, bạn hãy giúp Demen tìm ra hòn đảo nào cách hòn đảo ~U~ đúng ~K~ tuyến đường bí mật để Demen nhanh chóng tới được hòn đảo chứa kho báu Two Piece, biết đâu sau đó bạn sẽ được Demen chia cho một ít kho báu φ(゜▽゜*)♪.
Có ~Q~ hòn đảo mà Bedao có thể dịch chuyển Demen và băng hải tặc của cậu tới, với mỗi hòn đảo ~U_i~ và tấm vé thông hành có mã số ~K_i~ nhiệm vụ của bạn là giúp Demen tìm ra hòn đảo ~x~ bất kì sao cho từ hòn đảo ~x~ đến hòn đảo ~U_i~ có đúng ~K_i~ con đường bí mật.
Input
Dòng đầu tiên gồm số nguyên ~N~ ~(2 \le N \le 2 \times 10^5)~ là số lượng hòn đảo trên bản đồ.
~N-1~ dòng tiếp theo, mỗi dòng gồm 2 số nguyên ~u_i~, ~v_i~ mô tả con đường bí mật giữa 2 hòn đảo ~u_i~ và ~v_i~ ~(1 \le u_i, v_i \le N, u_i \neq v_i)~.
Dòng thứ ~N + 1~ chứa số nguyên ~Q~, ~(1 \le Q \le 2 \times 10^5)~ là số hòn đảo mà Bedao có thể dịch chuyển Demen và băng hải tặc của cậu tới.
~Q~ dòng tiếp theo, mỗi dòng gồm 2 số nguyên ~U_i~, ~K_i~ lần lượt là hòn đảo mà Bedao có thể dịch chuyển Demen và băng hải tặc của cậu tới và mã số trên tấm vé thông hành ~(1 \le U_i, K_i \le N)~.
Output
In ra ~Q~ dòng, mỗi dòng in ra chỉ số của hòn đảo ~x~ bất kì sao cho từ hòn đảo ~x~ đến hòn đảo ~U_i~ có đúng ~K_i~ con đường bí mật.
Nếu không tìm được đỉnh ~x~ nào thỏa yêu cầu, in ~-1~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | ~25~ | ~N \times Q \le 3 \times 10^6~ |
| ~2~ | ~75~ | Không có giới hạn gì thêm. |
Sample Input 1
5
1 2
2 3
3 4
3 5
3
2 2
5 3
3 3
Sample Output 1
4
1
-1
Sample Input 2
10
1 2
2 3
3 5
2 8
3 4
4 6
4 9
5 7
9 10
5
1 1
2 2
3 3
4 4
5 5
Sample Output 2
2
4
10
-1
-1
Notes
Ở ví dụ thứ nhất,
Từ hòn đảo đầu tiên, ~U_1 = 2~, có hai hòn đảo có khoản cách đúng bằng ~K_1 = 2~ mà ~Bedao~ có thể dịch chuyển ~Demen~ đến là ~4~, và ~5~.
Từ hòn đảo thứ hai, ~U_2 = 5~, có đúng một hòn đảo có khoản cách đúng bằng ~K_2 = 3~ mà ~Bedao~ có thể dịch chuyển ~Demen~ đến là hòn đảo ~1~.
Từ hòn đảo thứ ba ~U_3 = 3~, Không có hòn đảo nào thỏa mãn điều kiện.
Ở ví dụ thứ hai,
Chỉ có một hòn đảo thỏa mãn điều kiện là hòn đảo ~2~.
Có hai hòn đảo thỏa mãn điều kiện là hòn đảo ~4, 5~.
Chỉ có một hòn đảo thỏa mãn điều kiện là hòn đảo ~10~.
không có hòn đảo nào thỏa cả hai điều kiện còn lại.
Điểm: 100
Để trang trí nhà cửa cho dịp Noel, Minh quyết định dùng lại một cái cây cậu nhặt được từ một bài toán trước đó.
Cây ở đây là một đồ thị liên thông gồm có ~n~ đỉnh và ~n-1~ cạnh, với gốc là đỉnh ~1~. Ngoài cái cây này ra, Minh cũng có một số quả cầu pha lê với ~k~ màu khác nhau. Trên mỗi đỉnh ~i~, Minh gắn một quả cầu có màu ~c_i~. Sau khi gắn xong, Minh tính độ bắt mắt của mỗi đỉnh. Độ bắt mắt của một đỉnh ~v~ bằng số màu phân biệt có trong các quả cầu pha lê gắn trên các đỉnh của cây con có gốc là đỉnh ~v~.
Nhận thấy cây chưa đủ đẹp, Minh thực hiện thêm ~m~ thao tác. Mỗi thao tác thuộc một trong hai loại:
Loại 1: Minh thay quả cầu gắn trên đỉnh ~a~ bằng quả cầu có màu ~b~.
Loại 2: Minh muốn biết độ bắt mắt của đỉnh ~a~.
Vì đã quá mệt mỏi sau khi phải tính độ bắt mắt cho toàn bộ cây ban đầu, Minh muốn bạn tính hộ cậu độ bắt mắt trong mỗi thao tác loại 2.
Input
Dòng đầu tiên gồm 3 số ~n, k, m\ (1 \le k \le n)~.
Dòng tiếp theo gồm ~n~ số ~c_1,\ c_2,\ ...\ c_n~ ~(1 \le c_i \le k)~
~n-1~ dòng tiếp theo, mỗi dòng gồm 2 số ~u,\ v~ cho biết một cạnh ~(u,v)~ của cây ~(1 \le u, v \le n, u \neq v)~.
~m~ dòng tiếp theo, mỗi dòng cho biết một thao tác. Mỗi dòng thuộc 1 trong 2 dạng:
~1\ a\ b~: Minh thay quả cầu gắn trên đỉnh ~a~ bằng quả cầu có màu ~b~. ~(1 \le a \le n,\ 1 \le b \le k)~
~2\ a~: Minh muốn biết độ bắt mắt của đỉnh ~a~. ~(1 \le a \le n)~
Output
Với mỗi thao tác loại 2, in ra một dòng cho biết độ bắt mắt của đỉnh ~a~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~10~ | ~1 \le n, m \le 2000~ |
| 2 | ~20~ | ~1 \le n, m \le 200000~ và không có thao tác loại 1 |
| 3 | ~40~ | ~1 \le n, m \le 200000~ |
| 4 | ~30~ | ~1 \le n \le 500000,\ 1 \le m \le 300000~ |
Sample Input 1
5 5 5
3 4 1 1 2
1 2
1 3
2 4
2 5
2 2
2 1
1 2 1
2 2
2 1
Sample Output 1
3
4
2
3
Sample Input 2
7 5 4
1 2 3 4 3 2 1
1 2
1 3
1 4
4 5
4 6
4 7
2 4
2 1
2 2
2 7
Sample Output 2
4
4
1
1
Notes
Hình minh họa sample 1:
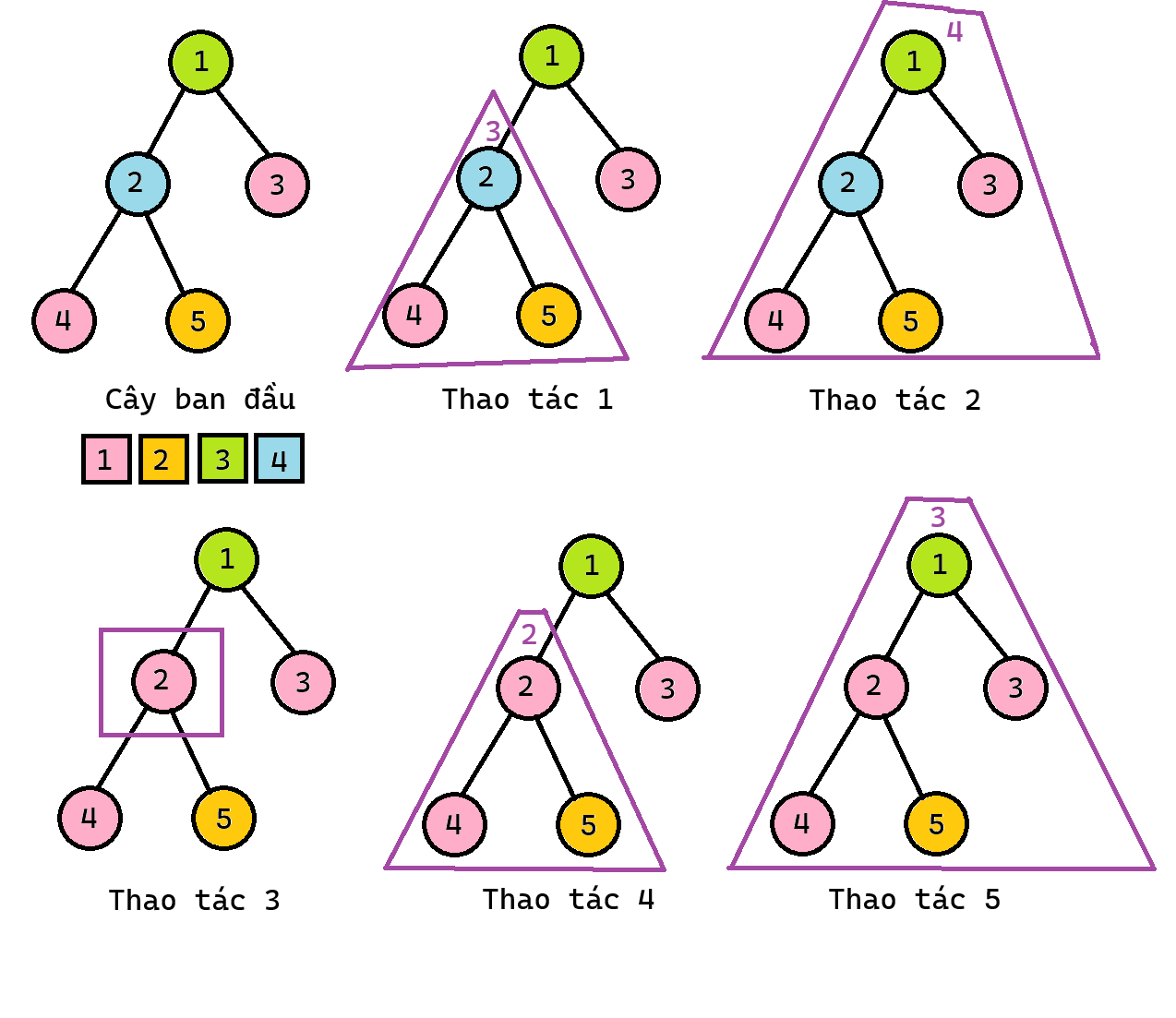
Hình minh họa sample 2:
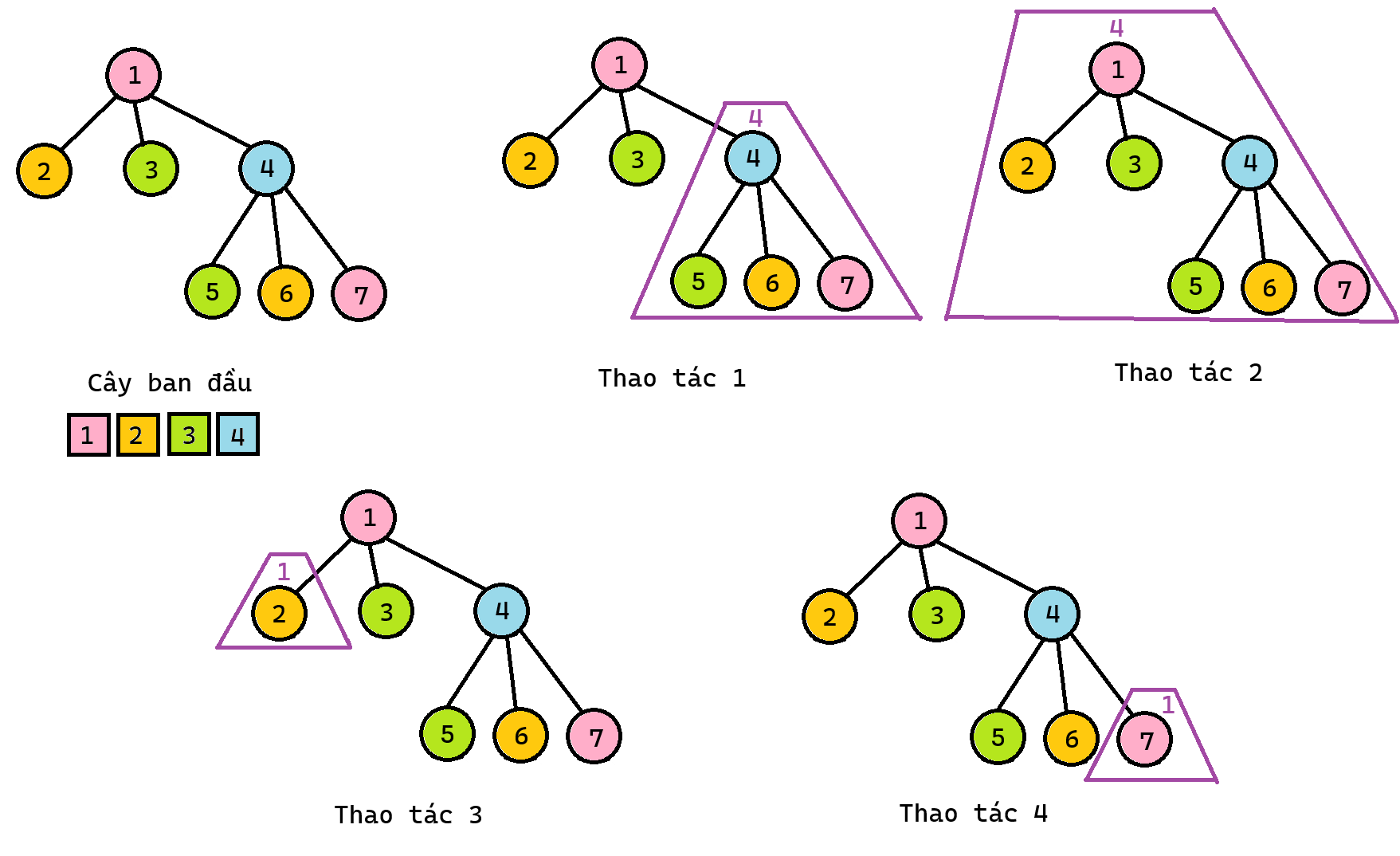
Điểm: 100
Cho một cây gồm ~n~ đỉnh và ~n - 1~ cạnh, gốc cây tại nút ~1~.
Trả lời ~q~ truy vấn có dạng:
- ~u~ ~v~: Đâu là tổ tiên chung thấp nhất của ~u~ và ~v~ (hay còn được gọi là ~lca(u, v)~)?
Gọi ~x_i~ là đáp án của truy vấn thứ ~i~ (~1 \leq i \leq q~), yêu cầu xuất ra giá trị ~ans~ = ~x_1\ \oplus\ x_2\ \oplus\ ...\ \oplus\ x_q~, với ~\oplus~ là phép toán XOR.
Input
Dòng đầu tiên gồm ~2~ số nguyên dương ~n~ và ~q~ (~1 \leq n \leq 10^5~, ~1 \leq q \leq 10^7~).
Trong ~n - 1~ dòng tiếp theo, mỗi dòng chứa ~2~ số nguyên dương (~u~, ~v~) thể hiện một cạnh của cây, (~1 \leq u, v \leq n~, ~u \neq v~).
Các truy vấn sẽ được sinh bằng ~6~ số nguyên ~u_{start}~, ~v_{start}~, ~u_{jump}~, ~v_{jump}~, ~u_{add}~, ~v_{add}~ (~1 \leq u_{start}, v_{start} \leq n~, ~0 \leq u_{jump}, v_{jump}, u_{add}, v_{add} \leq 10^9~) như sau:
Trong truy vấn thứ ~1~, ~u_1~ = ~u_{start}~, ~v_1 = v_{start}~.
Từ truy vấn thứ ~i~ (~i > 1~), ~u_i~ = (~u_{i-1}~ ~\cdot~ ~u_{jump}~ + ~u_{add}~) mod ~n + 1~, ~v_i~ = (~v_{i-1}~ ~\cdot~ ~v_{jump}~ + ~v_{add}~) mod ~n + 1~.
Output
Gồm ~1~ dòng duy nhất chứa kết quả theo yêu cầu của bài toán.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | ~25~ | ~n, q \le 10^3~ |
| ~2~ | ~25~ | ~q \le 10^5~ |
| ~3~ | ~50~ | Không có ràng buộc gì gì thêm |
Sample Input 1
3 1
1 2
1 3
2 3 1 1 1 1
Sample Output 1
1
Sample Input 2
3 2
1 2
1 3
3 3 1 1 1 1
Sample Output 2
1
Notes
Ở test ví dụ đầu tiên, ta có truy vấn ~(u_1, v_1)~ ~=~ ~(2, 3)~ có tổ tiên chung thấp nhất là ~1~. Do đó, đáp án cho test này là ~ans = 1~.
Ở test ví dụ thứ hai, ta có ~2~ truy vấn ~(u_1, v_1) = (3, 3)~ và ~(u_2, v_2)~ ~=~ ~(3 \cdot 1 + 1~ mod ~3 + 1, 3 \cdot 1 + 1~ mod ~3 + 1) = (2, 2)~ có tổ tiên chung thấp nhất lần lượt là ~3~ và ~2~. Do đó, đáp án cho test này là ~ans = 3 \oplus 2 = 1~.
Điểm: 100
Cho một đồ thị vô hướng liên thông có ~n~ đỉnh và ~n - 1~ cạnh, với các đỉnh được đánh số từ ~1~ đến ~n~.
Ban đầu, các đỉnh đều được gán một giá trị - đỉnh ~i~ được gán giá trị ~v_{i}~.
Các bạn cần xử lý ~2~ loại truy vấn sau:
~1~ ~node~ ~val~: Cập nhật lại giá trị của đỉnh ~node~ thành ~val~
~2~ ~a~ ~b~: Hãy tính giá trị lớn nhất của một đỉnh trên đường đi từ ~a~ đến ~b~ (đảm bảo rằng có đúng một đường đi từ ~a~ đến ~b~)
Input
Dòng đầu tiên chứa ~2~ số ~n~ và ~q~ — số đỉnh và số truy vấn trong input
Dòng thứ hai chứa ~n~ số ~v_1, v_2, ..., v_n~
~q~ dòng tiếp theo, mỗi dòng chứa ~3~ số là thông tin của một truy vấn
Output
In ra một dòng chứa đáp án của truy vấn loại ~2~ theo cùng thứ tự với input.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | ~25~ | ~n, q \le 5000~ |
| ~2~ | ~25~ | ~n, q \le 75000~ |
| ~2~ | ~50~ | ~n, q \le 200000~ |
Sample Input 1
5 3
2 4 1 3 3
1 2
1 3
2 4
2 5
2 3 5
1 2 2
2 3 5
Sample Output 1
4 3
Sample Input 2
5 4
1 2 3 4 5
1 2
2 3
1 4
1 5
2 2 3
1 4 100
2 2 3
2 1 4
Sample Output 2
3 3 100
Notes
Giải thích test đề ~1~:
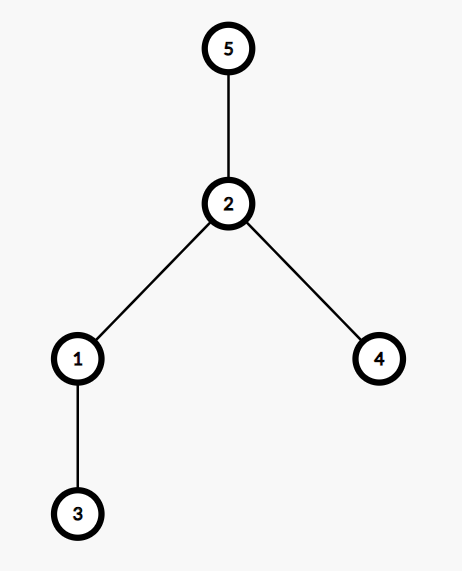
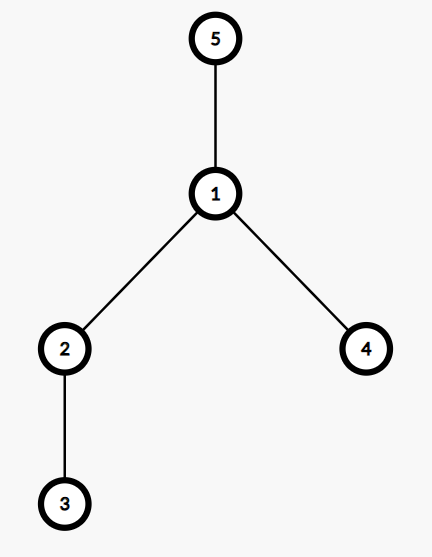
Ở truy vấn đầu tiên, các đỉnh trên đường đi giữa ~3~ và ~5~ là ~3, 1, 2, 5~. Trong các đỉnh đó, đỉnh ~2~ là đỉnh có giá trị lớn nhất (~4~).
Ở truy vấn thứ hai, đỉnh ~2~ được đặt lại giá trị bằng ~2~.
Ở truy vấn thứ ba, đỉnh ~4~ và ~5~ là các đỉnh có giá trị lớn nhất (~3~).
Giải thích test đề ~2~:
Ở truy vấn đầu tiên, các đỉnh trên đường đi giữa ~2~ và ~3~ là ~2~ và ~3~. Trong các đỉnh đó, đỉnh ~3~ là đỉnh có giá trị lớn nhất (~3~).
Ở truy vấn thứ hai, đỉnh ~4~ được đặt lại giá trị bằng ~100~.
Ở truy vấn thứ ba, các đỉnh ~2~ và ~3~ không được đặt lại giá trị, nên đáp án không đổi.
Ở truy vấn thứ tư, các đỉnh trên đường đi giữa ~1~ và ~4~ là ~1~ và ~4~. Trong các đỉnh đó, đỉnh ~4~ là đỉnh có giá trị lớn nhất (~100~)
Điểm: 100
Dế Mèn có một bài toán thú vị về cây như sau: cậu có một cây gồm ~n~ đỉnh, đỉnh thứ ~i~ có một hàm tuyến tính ~f_i(x) = a_i x + b_i~ và cạnh thứ ~i~ nối đỉnh ~u_i~ với ~v_i~. Bạn phải xử lý ~q~ truy vấn sau:
~0~ ~p~ ~c~ ~d~: Gán ~f_p~ thành ~cx + d~.
~1~ ~u~ ~v~ ~x~: Coi các đỉnh trên đường đi từ ~u~ đến ~v~ lần lượt là ~p_1 = u~, ~p_2~, ~\cdots~, ~p_k = v~. Tính ~f_{p_k}(...f_{p_2}(f_{p_1}(x)))~ ~\bmod~ ~998244353~
Input
Dòng đầu tiên chứa hai số nguyên ~n~ và ~q~ — số đỉnh và số truy vấn.
Trong ~n~ dòng sau, dòng thứ ~i~ gồm hai số nguyên ~a_i, b_i~ — chỉ số hàm tuyến tính của đỉnh ~i~.
Trong ~n - 1~ dòng kế tiếp, dòng thứ ~i~ gồm hai số nguyên ~u_i, v_i~ — cạnh ~i~ nối hai đỉnh ~u_i~ và ~v_i~.
Trong ~q~ dòng cuối cùng, truy vấn ~i~ thuộc một trong hai loại trên.
Constraints
~1 \le n, q \le 2 \times 10^5~
~1 \le a_i, c < 998244353~
~0 \le b_i, d, x < 998244353~
~1 \le p, u, v \le n~
~1 \le u_i, v_i \le n~
Output
Với mỗi truy vấn ~1~ in ra kết quả trên một dòng.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~30~ | ~1 \le n, q \le 5000~ |
| 2 | ~70~ | Không có ràng buộc gì thêm |
Sample Input 1
4 3
1 5
4 0
1 1
3 2
1 3
2 4
3 4
1 1 4 3
0 3 2 1
1 4 4 4
Sample Output 1
29
14
Notes
Ở truy vấn thứ nhất, ta có ~f_{4}(f_{3}(f_{1}(x))) = 3(1(1x + 5) + 1) + 2 = 3(1(3 + 5) + 1) + 2 = 29~
Ở truy vấn thứ hai, ta đặt ~f_{3}(x) = 2x + 1~
Ở truy vấn thứ ba, vì đường đi chỉ có một đỉnh nên ta có ~f_{4}(x) = 3x + 2 = 3 \cdot 4 + 2 = 14~
Điểm: 100
Dế Mèn có một cây có ~n~ đỉnh với đỉnh gốc ~1~. Đỉnh ~i~ có giá trị là ~a_i~. Ban đầu mọi đỉnh đều có giá trị ~0~. Thực hiện ~q~ truy vấn thuộc ~4~ loại sau trên cây:
~1~ ~u~ ~v~ ~val~ : Với mọi đỉnh ~i~ trên đường đi từ ~u~ đến ~v~, ~a_i = a_i + val~.
~2~ ~u~ ~val~ : Với mọi đỉnh ~i~ trong cây con của ~u~, ~a_i = a_i + val~.
~3~ ~u~ ~v~ : Cho biết giá trị ~a_i~ lớn nhất trong các đỉnh ~i~ trên đường đi từ ~u~ đến ~v~.
~4~ ~u~ : Cho biết giá trị ~a_i~ lớn nhất trong các đỉnh ~i~ thuộc cây con của ~u~.
Input
Dòng đầu nhập ~2~ số ~n~ và ~q~ ~(1 \le n, q \le 3 \times 10^5)~ lần lượt là số đỉnh của cây và số lượng truy vấn trên cây.
~n-1~ dòng tiếp theo, mỗi dòng nhập 2 số nguyên dương ~u~ và ~v~ ~(u \neq v, 1 \le u, v \le n)~ là một cạnh của cây.
~q~ dòng tiếp theo, mỗi dòng nhập một truy vấn thuộc ~4~ loại ~(1 \le u, v \le n, 1 \le val \le 10^9)~.
Output
In ra câu trả lời cho các truy vấn loại ~3~ và ~4~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~10~ | ~n \times q \le 3 \times 10 ^ 5~ |
| 2 | ~10~ | Chỉ gồm các truy vấn ~2~ và ~4~ |
| 3 | ~20~ | Chỉ gồm các truy vấn ~1~ và ~3~ |
| 4 | ~60~ | Không có ràng buộc gì thêm |
Sample Input 1
5 5
1 2
1 3
3 4
3 5
1 4 5 1
1 5 2 1
3 2 3
2 3 1
4 3
Sample Output 1
2
3
Sample Input 2
9 9
3 5
3 8
4 8
3 9
8 1
3 6
1 2
5 7
1 5 7 5
1 2 8 8
2 3 10
4 1
2 2 5
3 3 2
2 1 3
4 3
3 3 2
Sample Output 2
15
13
18
16
Notes
Trong test ví dụ đầu tiên, hình ảnh của cây ban đầu:
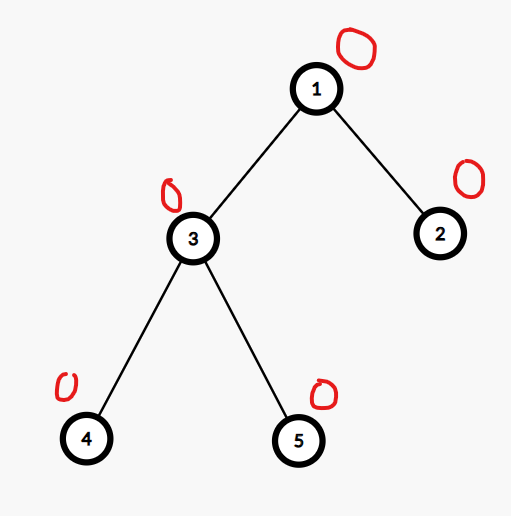
Sau truy vấn thứ ~1~, cây sẽ có dạng:
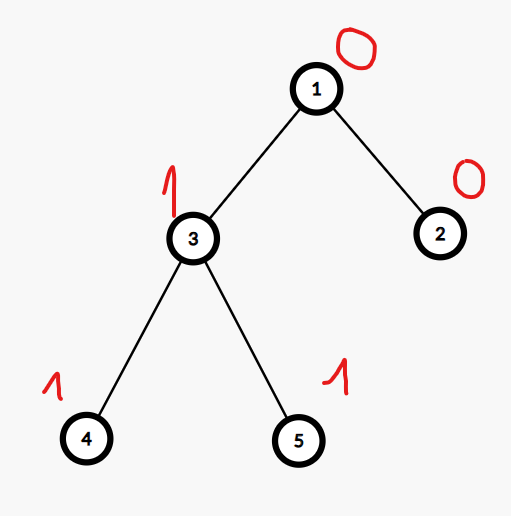
Sau truy vấn thứ ~2~, cây sẽ có dạng:
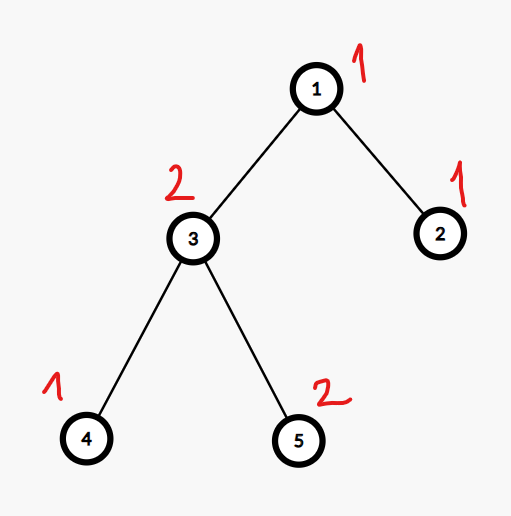
Trong truy vấn thứ ~3~, ta cần tìm giá trị lớn nhất trên đường đi từ ~2~ đến ~3~. Từ đó cho ra đáp án là: ~2~.
Sau truy vấn thứ ~4~, cây sẽ có dạng:
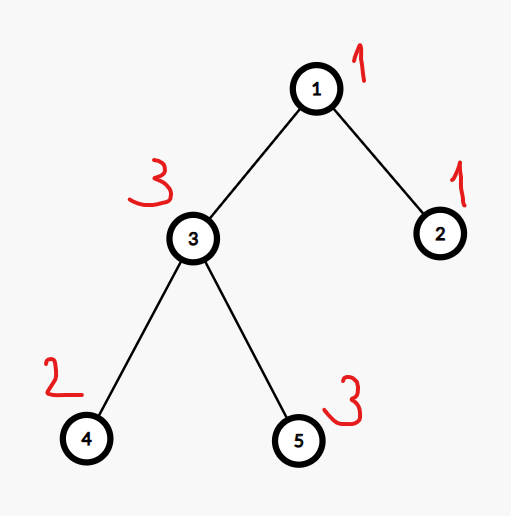
Trong truy vấn thứ ~5~, ta cần tìm giá trị lớn nhất trong cây con của đỉnh ~3~. Từ đó cho ra đáp án là: ~3~.
Trong test ví dụ thứ hai, hình ảnh của cây ban đầu:
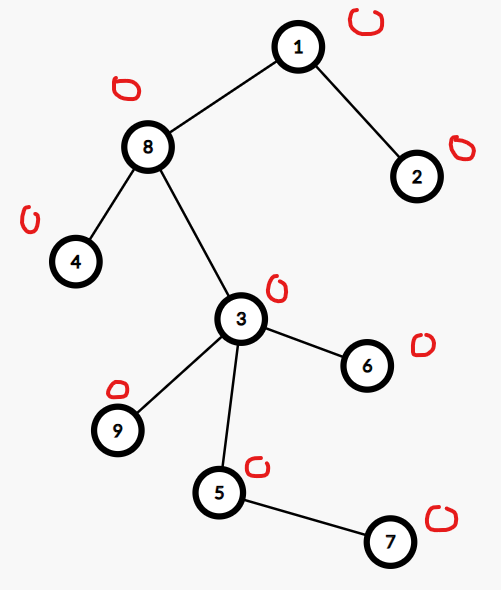
Sau truy vấn thứ ~1~, cây sẽ có dạng:
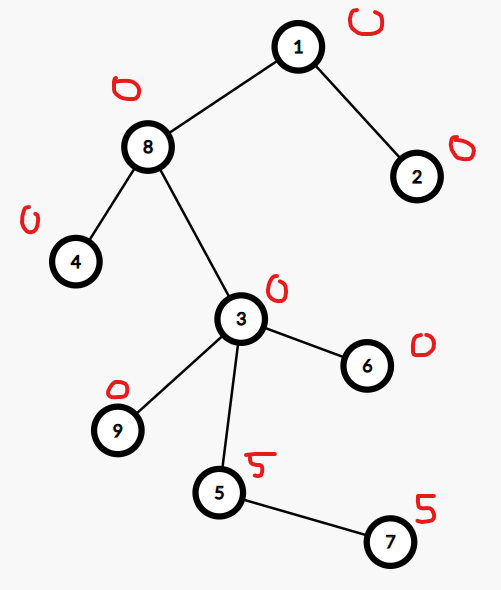
Sau truy vấn thứ ~2~, cây sẽ có dạng:

Sau truy vấn thứ ~3~, cây sẽ có dạng:
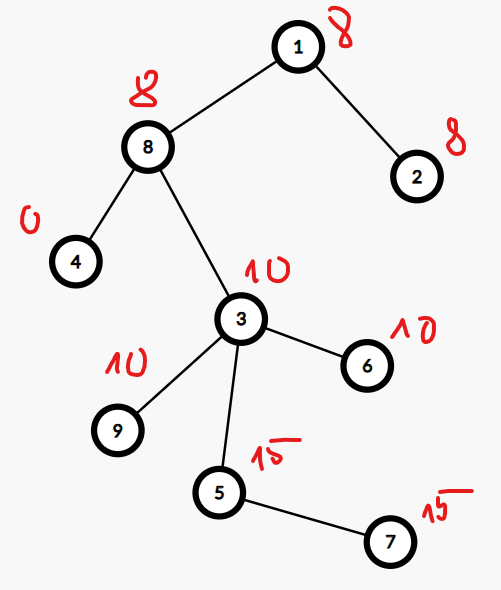
Trong truy vấn thứ ~4~, ta cần tìm giá trị lớn nhất trong cây con của đỉnh ~1~. Từ đó cho ra đáp án là: ~18~.
Sau truy vấn thứ ~5~, cây sẽ có dạng:
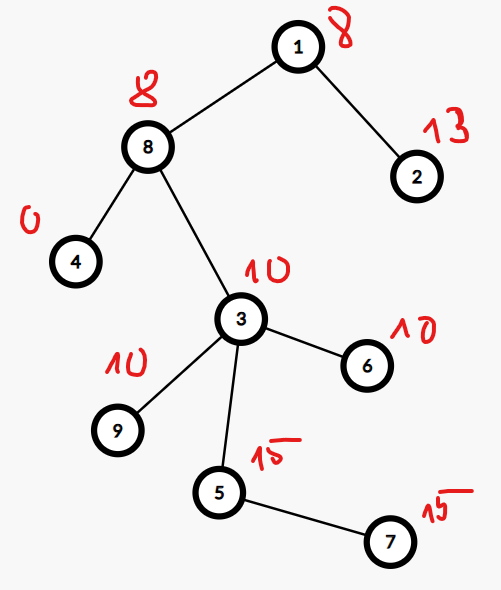
Trong truy vấn thứ ~6~, ta cần tìm giá trị lớn nhất trên đường đi từ ~3~ đến ~2~. Từ đó cho ra đáp án là: ~13~.
Sau truy vấn thứ ~7~, cây sẽ có dạng:
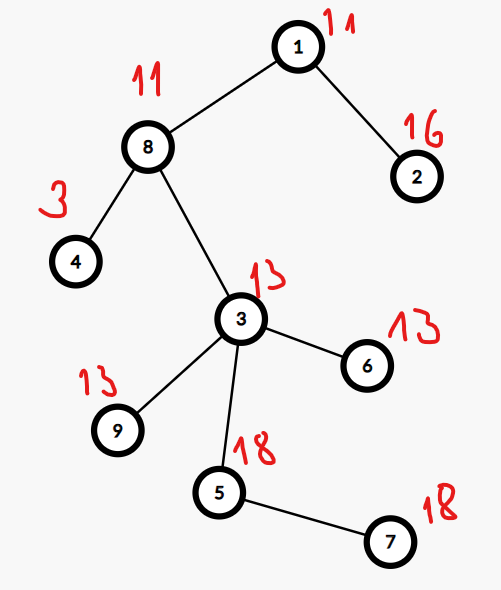
Trong truy vấn thứ ~8~, ta cần tìm giá trị lớn nhất trong cây con của đỉnh ~3~. Từ đó cho ra đáp án là: ~18~.
Trong truy vấn thứ ~9~, ta cần tìm giá trị lớn nhất trên đường đi từ ~3~ đến ~2~. Từ đó cho ra đáp án là: ~16~.
Điểm: 100
Trong vương quốc JOI có ~N~ thành phố, được đánh số từ ~1~ đến ~N~. Có ~N - 1~ con đường trong vương quốc JOI, được đánh số từ ~1~ đến ~N - 1~. Con đường thứ ~i~ (~1 \le i \le N - 1~) nối thành phố ~A_i~ và thành phố ~B_i~ theo cả hai hướng. Có thể đi từ bất kỳ thành phố nào đến bất kỳ thành phố nào khác bằng cách đi qua một số con đường.
Trên một số con đường trong vương quốc JOI có các trạm kiểm tra. Có ~M~ trạm kiểm tra, được đánh số từ ~1~ đến ~M~. Trạm kiểm tra thứ ~j~ (~1 \le j \le M~) nằm trên con đường ~P_j~. Để đi qua trạm kiểm tra đó, bạn cần trả một đồng vàng hoặc ~C_j~ đồng bạc.
Có ~Q~ công dân trong vương quốc JOI, được đánh số từ ~1~ đến ~Q~. Công dân thứ ~k~ (~1 \le k \le Q~) có ~X_k~ đồng vàng và ~Y_k~ đồng bạc, và muốn đi từ thành phố ~S_k~ đến thành phố ~T_k~. Vì đồng vàng có giá trị, tất cả công dân đều muốn giữ nhiều đồng vàng nhất có thể.
Hãy viết một chương trình, cho thông tin về các thành phố, con đường, các trạm kiểm tra và các công dân trong vương quốc JOI, với mỗi ~k~ (~1 \le k \le Q~), xác định xem công dân thứ ~k~ có thể đi từ thành phố ~S_k~ đến thành phố ~T_k~ không, và nếu có thể, tính toán số đồng vàng tối đa mà công dân thứ ~k~ có thể giữ.
Input
Dòng đầu tiên chứa ba số nguyên ~N~, ~M~, ~Q~ lần lượt là số thành phố, số trạm kiểm tra và số công dân trong vương quốc JOI (~2 \le N \le 100000~, ~1 \le M, Q \le 100000~).
~N - 1~ dòng tiếp theo, dòng thứ ~i~ chứa hai số nguyên ~A_i~ và ~B_i~ mô tả một con đường hai chiều (~1 \le A_i, B_i \le N~).
~M~ dòng tiếp theo, dòng thứ ~j~ chứa hai số nguyên ~P_j~ và ~C_j~ mô tả một trạm kiểm tra (~1 \le P_j \le N - 1~, ~1 \le C_j \le 10^9~).
~Q~ dòng cuối cùng, dòng thứ ~k~ chứa bốn số nguyên ~S_k~, ~T_k~, ~X_k~, ~Y_k~ mô tả mộ công dân (~1 \le S_k, T_k \le N~, ~S_k \neq T_k~, ~0 \le X_k \le 10^9~, ~0 \le Y_k \le 10^{18}~).
Output
In ra ~Q~ dòng. Trên dòng thứ ~k~ (~1 \le k \le Q~), nếu công dân thứ ~k~ có thể đi từ thành phố ~S_k~ tới thành phố ~T_k~, in ra số lượng đồng vàng nhiều nhất công dân thứ ~k~ có thể giữ. Ngược lại, in ra ~-1~ trên dòng thứ ~k~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | ~10~ | ~N \le 2000~, ~M \le 2000~, ~Q \le 2000~ |
| ~2~ | ~28~ | ~C_1 = C_2 = \ldots = C_M~ |
| ~3~ | ~30~ | ~A_i = i, B_i = i + 1 (1 \le i \le N - 1)~ |
| ~4~ | ~32~ | Không có ràng buộc gì thêm. |
Sample Input 1
5 4 3
1 2
1 3
2 4
2 5
2 9
2 4
3 5
4 7
3 4 2 11
5 3 4 5
2 3 1 1
Sample Output 1
1
2
-1
Sample Input 2
10 7 9
1 8
6 3
5 9
7 9
3 1
3 4
10 1
2 6
5 6
9 4
7 4
7 4
2 4
7 4
7 4
1 4
8 6 5 3
3 9 8 0
4 7 6 15
7 4 9 3
6 4 8 0
9 10 5 16
5 3 2 4
2 8 4 3
6 1 3 3
Sample Output 2
3
6
6
7
7
3
1
2
2
Sample Input 3
8 7 11
1 2
2 3
3 4
4 5
5 6
6 7
7 8
4 4
3 7
2 10
5 2
4 1
4 4
5 6
6 3 7 69
7 1 5 55
3 1 6 8
8 2 5 45
4 6 4 45
6 1 3 33
2 1 0 19
3 7 2 31
7 1 2 31
7 2 4 58
8 3 5 63
Sample Output 3
7
5
5
5
4
2
0
2
1
4
5
Sample Input 4
8 7 11
1 8
1 4
3 1
3 6
6 7
2 1
5 2
5 5
5 8
4 7
6 6
4 1
6 4
1 7
4 7 2 18
2 4 5 1
4 2 1 32
1 5 7 21
2 5 0 50
8 4 4 33
1 7 6 16
4 8 7 18
1 2 8 13
5 4 10 42
7 1 6 40
Sample Output 4
1
3
1
7
0
4
5
7
8
10
6
Notes
Trong ví dụ thứ nhất:
Công dân ~1~ có thể đi từ thành phố ~3~ đến thành phố ~4~ như sau:
Công dân ~1~ đi từ thành phố ~3~ đến thành phố ~1~ qua con đường ~2~. Có trạm kiểm tra ~1~ và ~2~ trên con đường ~2~. Công dân ~1~ trả ~1~ đồng vàng cho trạm kiểm tra ~1~ và ~4~ đồng bạc cho trạm kiểm tra ~2~. Sau đó, công dân ~1~ còn lại ~1~ đồng vàng và ~7~ đồng bạc.
Công dân ~1~ đi từ thành phố ~1~ đến thành phố ~2~ qua con đường ~1~. Vì không có trạm kiểm tra nào trên đường nên công dân ~1~ còn lại ~1~ đồng vàng và ~7~ đồng bạc.
Công dân ~1~ đi từ thành phố ~2~ tới thành phố ~4~ qua con đường ~3~. Có trạm kiểm tra ~3~ trên con đường ~3~. Công dân ~1~ trả ~5~ đồng bạc cho trạm kiểm tra ~3~. Sau đó, công dân ~1~ còn lại ~1~ đồng vàng và ~2~ đồng bạc.
Sau khi di chuyển, công dân ~1~ còn lại ~1~ đồng vàng. Vì không có cách để công dân ~1~ có thể di chuyển và giữ lại nhiều hơn ~1~ đồng vàng, in ra ~1~ ở dòng đầu tiên.
Công dân ~2~ có thể đi từ thành phố ~5~ đến thành phố ~3~ như sau:
Công dân ~2~ đi từ thành phố ~5~ đến thành phố ~2~ qua con đường ~4~. Có trạm kiểm tra ~4~ trên con đường ~4~. Công dân ~2~ trả ~1~ đồng vàng cho trạm kiểm tra ~4~. Sau đó, công dân ~2~ còn lại ~3~ đồng vàng và ~5~ đồng bạc.
Công dân ~2~ đi từ thành phố ~2~ đén thành phố ~1~ qua con đường ~1~. Vì không có trạm kiểm tra nào trên đường nên công dân ~2~ còn lại ~3~ đồng vàng và ~5~ đồng bạc.
Công dân ~2~ đi từ thành phố ~1~ đến thành phố ~3~ qua con đường ~2~. Có trạm kiểm tra ~1~ và ~2~ trên con đường ~2~. Công dân ~2~ trả ~1~ đồng vàng cho trạm kiểm tra ~1~ và ~4~ đồng bạc cho trạm kiểm tra ~2~. Sau đó, công dân ~2~ còn lại ~2~ đồng vàng và ~1~ đồng bạc.
Sau khi di chuyển, công dân ~2~ còn lại ~2~ đồng vàng. Vì không có cách để công dân ~2~ có thể di chuyển và giữ lại nhiều hơn ~2~ đồng vàng, in ra ~2~ ở dòng thứ hai.
Không có cách nào để công dân ~3~ có thể đi từ thành phố ~2~ đến thành phố ~3~ với lượng tiền đang có, in ra ~-1~ ở dòng thứ ba.
Điểm: 100
A là một cậu bé đam mê tốc độ và những buổi biểu diễn đua xe tại trường đua. Hôm nay là ngày tổ chức sự kiện đua xe hằng năm, A có dự định sẽ đến trường đua gần nhà để xem những màn đua xe đẹp mắt.
Trường đua có dạng cây gồm ~n~ đỉnh đánh số từ ~1~ đến ~n~. Có ~m~ tay đua, tay đua thứ ~i~ sẽ trình diễn đua xe từ đỉnh ~u_i~ đến đỉnh ~v_i~ tại mốc thời gian ~t_i~ (đơn vị thời gian) với vận tốc không đổi ~s_i~ (cạnh / đơn vị thời gian). Trước mốc thời gian ~t_i~, xem như tay đua chưa xuất hiện trên trường đua.
Vì rất háo hức được thấy các tay lái, A muốn lựa chọn chỗ ngồi trong số ~n~ đỉnh của trường đua sao cho thời gian nhìn thấy được một tay đua bất kỳ là sớm nhất. Biết trước thời gian chạy của từng tay đua, bạn hãy giúp A tính toán xem với mỗi đỉnh thì thời gian sớm nhất gặp được một tay đua bất kỳ tính từ mốc thời gian ~0~ là bao nhiêu nhé.
Input
Dòng đầu tiên chứa một số nguyên ~T~ (~1 \le T \le 100~) cho biết số lượng test. Mỗi test được miêu tả như sau:
Dòng đầu tiên của mỗi test chứa một số nguyên dương ~n~ (~1\le n \le 2\times 10^5~).
~n-1~ dòng tiếp theo, mỗi dòng chứa 3 số nguyên dương lần lượt là ~u~, ~v~ và ~w~ (~1\le w\le 10^9~) cho biết trong cây có một cạnh nối giữa ~u~ và ~v~ với độ dài ~w~.
Dòng tiếp theo chứa số nguyên dương ~m~ (~1\le m \le 2\times 10^5~).
Dòng thứ ~i~ trong số ~m~ dòng tiếp theo chứa 4 số nguyên dương lần lượt là ~u_i~, ~v_i~, ~t_i~ và ~s_i~ (~1\le t_i, s_i \le 10^9~) cho biết thông tin của tay đua thứ ~i~.
Dữ liệu đảm bảo tổng các ~n~ và tổng các ~m~ trong số ~T~ test không vượt quá ~2\times 10^5~.
Output
Với mỗi test, in ra ~n~ dòng, dòng thứ ~i~ là thời gian sớm nhất mà đỉnh ~i~ nhìn thấy một tay đua bất kỳ, nếu không có tay đua nào xuất hiện, hay in ra ~-1~. Đáp án sẽ được chấp nhận nếu sai số không quả ~10^{-6}~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~10~ | ~\sum n, \sum m \le 5 \times 10^3~ |
| 2 | ~20~ | Vận tốc của các tay đua trong một test như nhau |
| 3 | ~20~ | Cây có thể biểu diễn thành một đường thẳng |
| 4 | ~50~ | Không có ràng buộc gì thêm |
Sample Input 1
1
5
1 2 3
1 3 5
3 4 1
4 5 4
3
2 1 3 4
4 2 1 3
1 3 2 6
Sample Output 1
2.0000000
3.0000000
1.3333333
1.0000000
-1