Minh và cây bắt mắt
Xem dạng PDFĐể trang trí nhà cửa cho dịp Noel, Minh quyết định dùng lại một cái cây cậu nhặt được từ một bài toán trước đó.
Cây ở đây là một đồ thị liên thông gồm có ~n~ đỉnh và ~n-1~ cạnh, với gốc là đỉnh ~1~. Ngoài cái cây này ra, Minh cũng có một số quả cầu pha lê với ~k~ màu khác nhau. Trên mỗi đỉnh ~i~, Minh gắn một quả cầu có màu ~c_i~. Sau khi gắn xong, Minh tính độ bắt mắt của mỗi đỉnh. Độ bắt mắt của một đỉnh ~v~ bằng số màu phân biệt có trong các quả cầu pha lê gắn trên các đỉnh của cây con có gốc là đỉnh ~v~.
Nhận thấy cây chưa đủ đẹp, Minh thực hiện thêm ~m~ thao tác. Mỗi thao tác thuộc một trong hai loại:
Loại 1: Minh thay quả cầu gắn trên đỉnh ~a~ bằng quả cầu có màu ~b~.
Loại 2: Minh muốn biết độ bắt mắt của đỉnh ~a~.
Vì đã quá mệt mỏi sau khi phải tính độ bắt mắt cho toàn bộ cây ban đầu, Minh muốn bạn tính hộ cậu độ bắt mắt trong mỗi thao tác loại 2.
Input
Dòng đầu tiên gồm 3 số ~n, k, m\ (1 \le k \le n)~.
Dòng tiếp theo gồm ~n~ số ~c_1,\ c_2,\ ...\ c_n~ ~(1 \le c_i \le k)~
~n-1~ dòng tiếp theo, mỗi dòng gồm 2 số ~u,\ v~ cho biết một cạnh ~(u,v)~ của cây ~(1 \le u, v \le n, u \neq v)~.
~m~ dòng tiếp theo, mỗi dòng cho biết một thao tác. Mỗi dòng thuộc 1 trong 2 dạng:
~1\ a\ b~: Minh thay quả cầu gắn trên đỉnh ~a~ bằng quả cầu có màu ~b~. ~(1 \le a \le n,\ 1 \le b \le k)~
~2\ a~: Minh muốn biết độ bắt mắt của đỉnh ~a~. ~(1 \le a \le n)~
Output
Với mỗi thao tác loại 2, in ra một dòng cho biết độ bắt mắt của đỉnh ~a~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~10~ | ~1 \le n, m \le 2000~ |
| 2 | ~20~ | ~1 \le n, m \le 200000~ và không có thao tác loại 1 |
| 3 | ~40~ | ~1 \le n, m \le 200000~ |
| 4 | ~30~ | ~1 \le n \le 500000,\ 1 \le m \le 300000~ |
Sample Input 1
5 5 5
3 4 1 1 2
1 2
1 3
2 4
2 5
2 2
2 1
1 2 1
2 2
2 1
Sample Output 1
3
4
2
3
Sample Input 2
7 5 4
1 2 3 4 3 2 1
1 2
1 3
1 4
4 5
4 6
4 7
2 4
2 1
2 2
2 7
Sample Output 2
4
4
1
1
Notes
Hình minh họa sample 1:
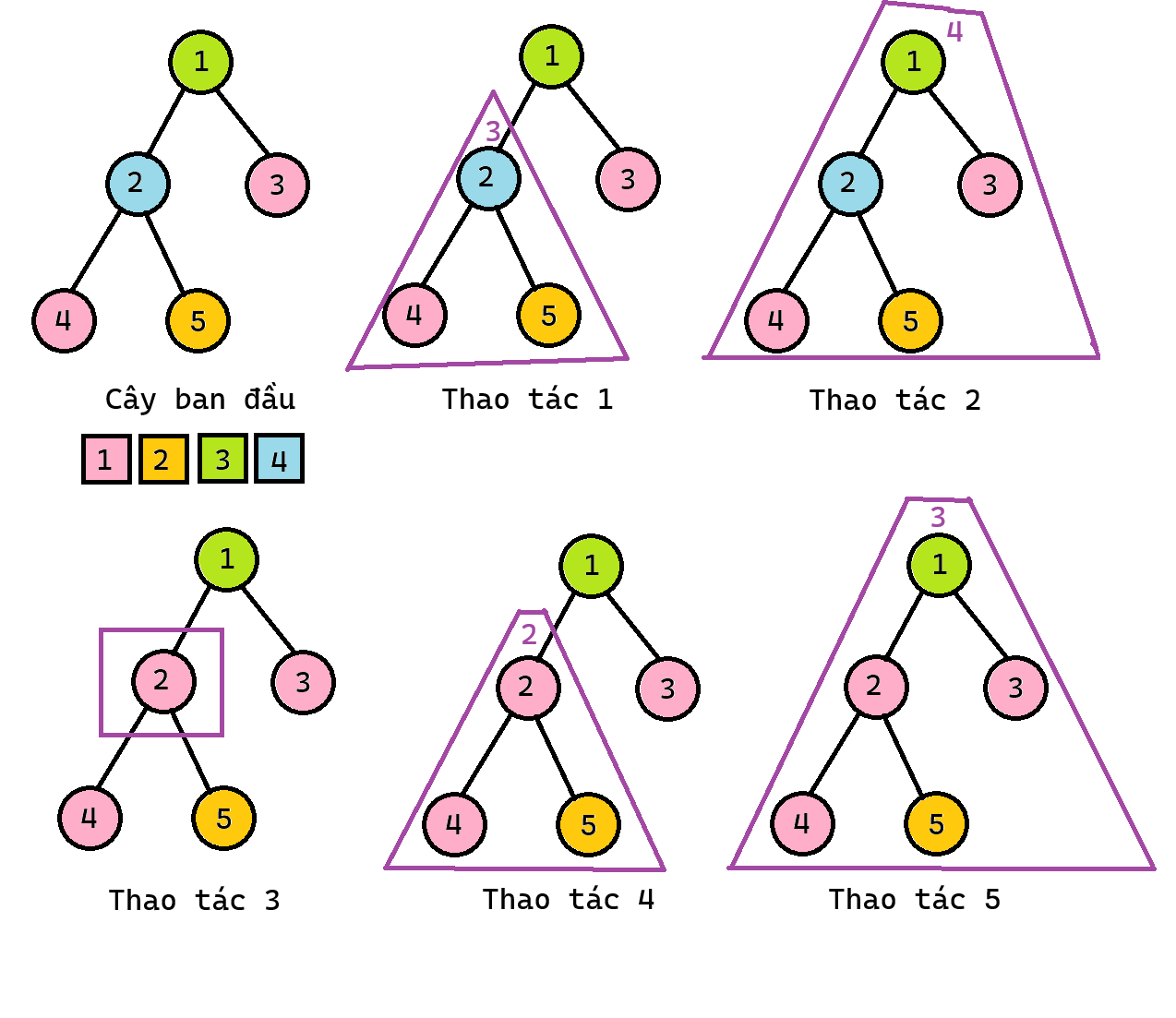
Hình minh họa sample 2:
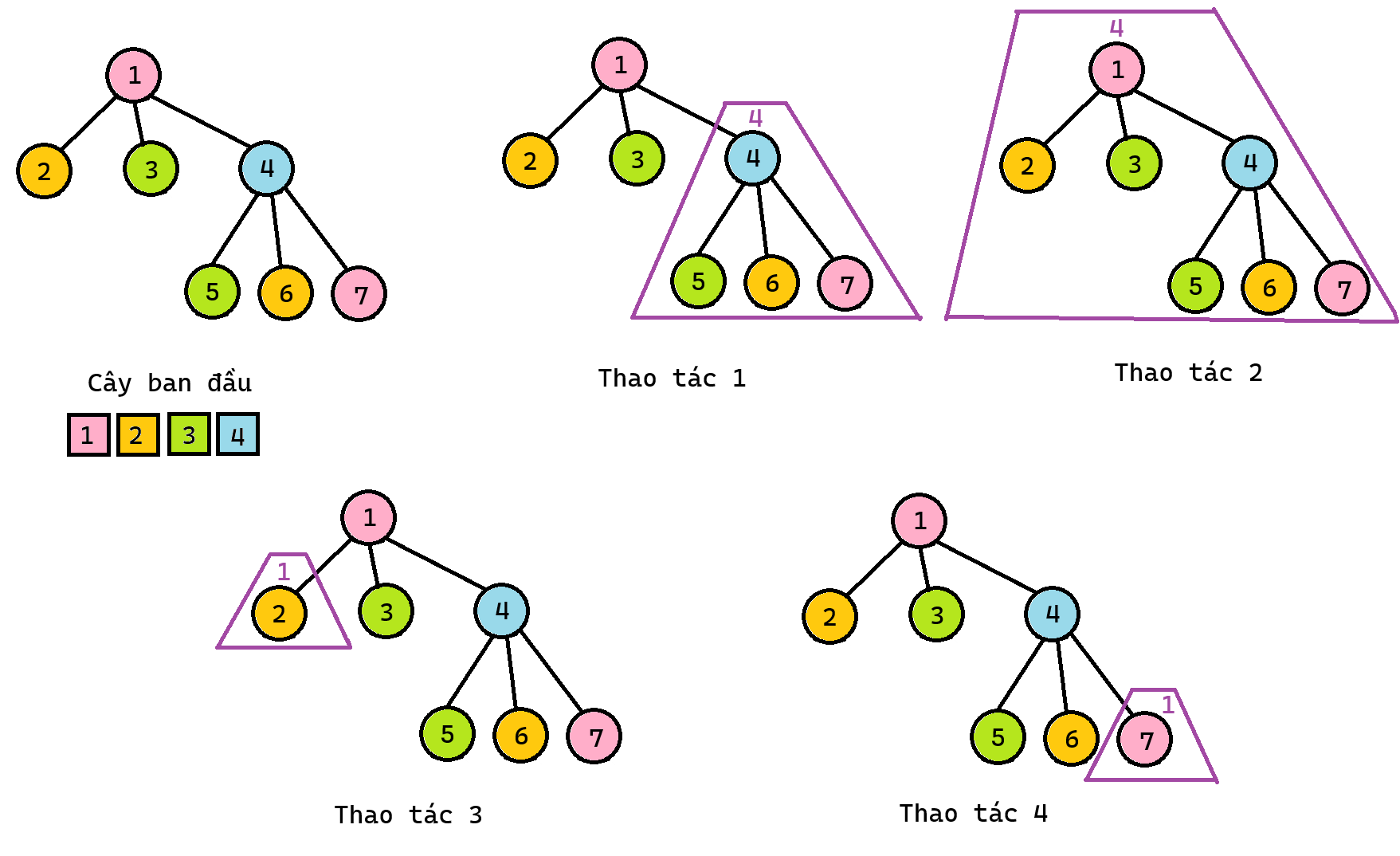

Bình luận
Bình luận này đã bị ẩn vì có quá nhiều phản ứng tiêu cực. Nhấn để xem.