Lại là bài truy vấn đường đi
Xem dạng PDFCho một đồ thị vô hướng liên thông có ~n~ đỉnh và ~n - 1~ cạnh, với các đỉnh được đánh số từ ~1~ đến ~n~.
Ban đầu, các đỉnh đều được gán một giá trị - đỉnh ~i~ được gán giá trị ~v_{i}~.
Các bạn cần xử lý ~2~ loại truy vấn sau:
~1~ ~node~ ~val~: Cập nhật lại giá trị của đỉnh ~node~ thành ~val~
~2~ ~a~ ~b~: Hãy tính giá trị lớn nhất của một đỉnh trên đường đi từ ~a~ đến ~b~ (đảm bảo rằng có đúng một đường đi từ ~a~ đến ~b~)
Input
Dòng đầu tiên chứa ~2~ số ~n~ và ~q~ — số đỉnh và số truy vấn trong input
Dòng thứ hai chứa ~n~ số ~v_1, v_2, ..., v_n~
~q~ dòng tiếp theo, mỗi dòng chứa ~3~ số là thông tin của một truy vấn
Output
In ra một dòng chứa đáp án của truy vấn loại ~2~ theo cùng thứ tự với input.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | ~25~ | ~n, q \le 5000~ |
| ~2~ | ~25~ | ~n, q \le 75000~ |
| ~2~ | ~50~ | ~n, q \le 200000~ |
Sample Input 1
5 3
2 4 1 3 3
1 2
1 3
2 4
2 5
2 3 5
1 2 2
2 3 5
Sample Output 1
4 3
Sample Input 2
5 4
1 2 3 4 5
1 2
2 3
1 4
1 5
2 2 3
1 4 100
2 2 3
2 1 4
Sample Output 2
3 3 100
Notes
Giải thích test đề ~1~:
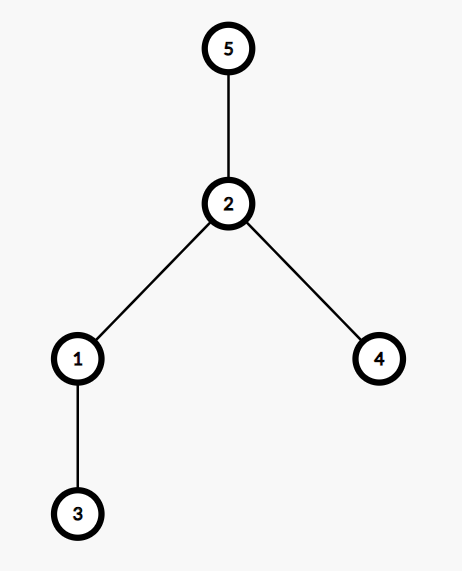
Ở truy vấn đầu tiên, các đỉnh trên đường đi giữa ~3~ và ~5~ là ~3, 1, 2, 5~. Trong các đỉnh đó, đỉnh ~2~ là đỉnh có giá trị lớn nhất (~4~).
Ở truy vấn thứ hai, đỉnh ~2~ được đặt lại giá trị bằng ~2~.
Ở truy vấn thứ ba, đỉnh ~4~ và ~5~ là các đỉnh có giá trị lớn nhất (~3~).
Giải thích test đề ~2~:
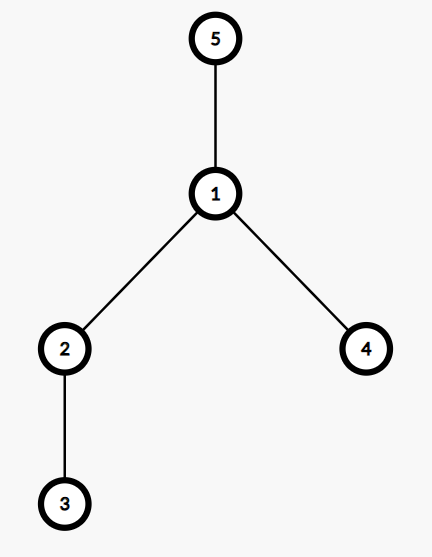
Ở truy vấn đầu tiên, các đỉnh trên đường đi giữa ~2~ và ~3~ là ~2~ và ~3~. Trong các đỉnh đó, đỉnh ~3~ là đỉnh có giá trị lớn nhất (~3~).
Ở truy vấn thứ hai, đỉnh ~4~ được đặt lại giá trị bằng ~100~.
Ở truy vấn thứ ba, các đỉnh ~2~ và ~3~ không được đặt lại giá trị, nên đáp án không đổi.
Ở truy vấn thứ tư, các đỉnh trên đường đi giữa ~1~ và ~4~ là ~1~ và ~4~. Trong các đỉnh đó, đỉnh ~4~ là đỉnh có giá trị lớn nhất (~100~)

Bình luận
Về input: Sau dòng thứ ~2~ là ~n - 1~ dòng, mỗi dòng chứa hai số ~u, v~ biểu diễn ~1~ cạnh vô hướng ~(u, v)~ của đồ thị. Sau đó mới là ~q~ dòng truy vấn nhé.