DYTECHLAB ALGORITHMS BATTLE 2023
Điểm: 1
 |
- Sau 6 năm sống ẩn mình trong hang động, ta, Piccôlô, đứa con của Đại Ma Vương Piccôlô, đã trở lại. Sức mạnh đã là hơn ~9000~, và không một con quỷ nào có thể cản bước được ta trở thành nhân vật chủ đề của AlgoBattle năm nay nữa! |
Piccôlô truy tìm Mabư Béo - kẻ thù truyền kiếp của hắn, và cũng là nhân vật chính trong Dytechlab AlgoBattle 2022 - để thách đấu và chọn ra kẻ mạnh nhất, để làm nhân vật chính cho cốt truyện năm nay.
Mabư Béo dự đoán trước được điều này. Hắn đã bỏ ra nhiều tháng trời để học hỏi, nghiên cứu về đứa con của Đại Ma Vương hùng mạnh đó. Hắn đã học hỏi từ những kẻ đã đánh bại Piccôlô - hạt giống số Một từ vùng đất của chính Đại Ma Vương - và thậm chí đã chiến thắng họ nhiều lần. Tuy nhiên, điều đó không thể đảm bảo chiến thắng cho Mabư Béo, đặc biệt là khi ở trận đấu này, Piccôlô được thi đấu trên sân nhà.
Trận đấu bắt đầu bằng một cuộc "tung đồng xu". Ai thắng sẽ có lợi thế chọn phần sân (xanh hoặc đỏ), và chọn đạo cụ chiến đấu. Lợi dụng khả năng thông thạo Tin học của mình sau một năm được làm ở Dytechlab, Mabư Béo đã hack vào hệ thống tung đồng xu, để thay đổi thuật toán sinh ngẫu nhiên của trò đó. Nói một cách vắn tắt, thuật toán sẽ sinh ngẫu nhiên một số nguyên ~N~, và sẽ chỉ hiện ra mặt mà có lợi cho Piccôlô khi mà ~N~ thỏa mãn:
- Tồn tại ~p, q~ là những số nguyên, sao cho: ~q \ge 2~ và ~p ^ q = N~.
Tỷ lệ dành chiến thắng cho Piccôlô ở trò tung đồng xu này từ ~50\%~ đã giảm xuống chỉ còn dưới ~1\%~ sau khi Mabư Béo cài thành công thuật toán. Mặc dù vậy, đó là trò duy nhất mà Mabư Béo dành được chiến thắng. Hai đấu sĩ đã có một kèo đấu "chênh lệch", khi Piccôlô đã "out trình" toàn thắng cả ba hiệp đấu, trong khi Mabư Béo thể hiện một bộ mặt đầy e thẹn và thiếu sáng.
Đối với bạn: bạn được cho số ~N~, hãy kiểm tra xem ai là người thắng cuộc tung đồng xu nhé!
Input
Dòng đầu tiên chứa ~T~ (~1 \le T \le 100~) - số test trong một tệp đầu vào. Mỗi test sẽ có định dạng như sau:
- Một dòng duy nhất chứa số nguyên ~N~ (~|N| \le 10^{16}~) - chứa số nguyên cần được kiểm tra.
Output
Với mỗi bộ test, in ra trên một dòng: "Piccolo" nếu tìm được ~p, q~ tương ứng, hoặc "Majin Buu" nếu ngược lại.
Sample Input 1
10
2
4
8
-2
-4
-8
729
-729
1
-1
Sample Output 1
Majin Buu
Piccolo
Piccolo
Majin Buu
Majin Buu
Piccolo
Piccolo
Piccolo
Piccolo
Piccolo
Notes
Dưới đây là giải thích cho từng test:
~2~ không thể phân tích được.
~4 = 2^2~.
~8 = 2^3~.
~-2~ không thể phân tích được.
~-4~ không thể phân tích được.
~-8 = (-2)^3~.
~729 = 3^6~.
~-729 = (-9)^3~.
~1 = 1 ^ {1000000000}~.
~-1 = (-1) ^ {2122023}~.
Điểm: 1
 |
Sau khi đánh bại Mabư Béo, nhiệm vụ tiếp theo của Piccôlô chính là ở lại quê nhà, xây dựng một Võ đài để cho các đấu sĩ trẻ có thể luyện tập một cách hiệu quả hơn. |
Vùng đất của Đại Ma Vương Piccôlô có thể được thể hiện bằng hệ trục tọa độ ~Oxy~. Võ đài mà Piccôlô xây nên sẽ là một hình chữ nhật, mà các điểm góc của nó đều có tọa độ nguyên.
Ở trong võ đài, ta sẽ xây một số "Trạm Mana" để tiếp sức cho các đấu sĩ, cũng như cho phép họ sử dụng các chiêu thức sáng tạo, tận dụng những trạm này để giành lấy lợi thế cho bản thân. Tuy nhiên, Trạm Mana sẽ chỉ có thể đặt được ở các vị trí có tọa độ nguyên dương ~(x, y)~ mà thỏa mãn tính chất đặc biệt: ~x * y~ là một số nửa nguyên tố.
Ta định nghĩa số nửa nguyên tố là tích của hai số nguyên tố khác nhau. Chẳng hạn: ~6, 10, 21~ là những số nửa nguyên tố, nhưng ~1, 3, 30, 9~ thì không phải.
Piccôlô nhận được ~N~ đề xuất cho các vị trí khác nhau để xây dựng võ đài. Mỗi đề xuất có dạng ~a, b, c, d~, thể hiện rằng võ đài đặt ở vị trí hình chữ nhật, có góc trái dưới ở điểm ~(a, b)~, và góc phải trên đặt ở đỉnh ~(c, d)~. Nhiệm vụ của bạn: với mỗi đề xuất, hãy tính số điểm có thể đặt Trạm Mana trên Võ đài.
Trạm Mana có thể được đặt ở cả điểm góc, lẫn điểm nằm trên cạnh của hình chữ nhật.
Input
Dòng đầu chứa ~N~ (~1 \le N \le 10^5~) - số đề xuất Piccôlô nhận được.
~N~ dòng sau, mỗi dòng chứa bốn số: ~a, b, c, d~ (~1 \le a \le c \le 10^6~, ~1 \le b \le d \le 10^6~), thể hiện giới hạn của hình chữ nhật trong mỗi đề xuất.
Output
Với mỗi đề xuất, in ra trên một dòng một số nguyên duy nhất, ứng với số điểm bạn tìm được.
Sample Input 1
5
2 2 7 5
1 3 2 8
1 1 1000 1000
1 1 1000000 1000000
99999 99999 1000000 1000000
Sample Output 1
9
4
28632
6162277240
4747967930
Notes
Đối với hình chữ nhật thứ nhất trong bộ test, ~9~ điểm được đánh dấu dưới đây là những điểm thỏa mãn:
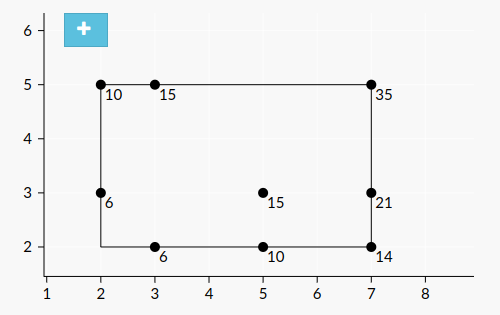
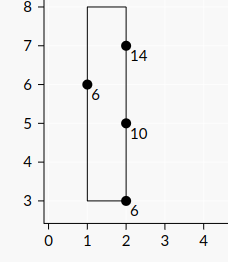
Đối với hình chữ nhật thứ hai trong bộ test, ~4~ điểm được đánh dấu dưới đây là những điểm thỏa mãn:
Điểm: 1
| "Các bài tập trên địa hình khác nhau rất quan trọng để tạo nên một đấu sĩ xuất sắc." |  |
Sau khi xuống dưới hang thăm người bạn thân của mình, Fanmu, Piccôlô cần phải tìm cách nhanh nhất để sử dụng chiêu thức của mình, trèo lại lên trên mặt đất, trước khi bị bầy quỷ tìm đến và có ý định ám sát.
Để làm được điều này, hắn ta phải sử dụng những tấm ván, đã được lắp sẵn vuông góc với hai bức tường thẳng đứng. Hai bức tường này song song với nhau, cách nhau ~W~ cm, và vuông góc với mặt đất. Với mỗi tấm ván có chỉ số ~i~, hắn ta biết ba thông tin:
Được lắp vuông góc với bức tường trái, hay phải ('L' hay 'R').
Có độ dài là ~a_i~ (cm) (~a_i \le \lfloor\frac{W}{2}\rfloor~), tức là điểm xa nhất trên tấm ván sẽ cách bức tường nó được lắp lên là độ dài này.
Có độ cao là ~h_i~ (cm) so với đáy hang.
Piccôlô đang đứng sẵn ở trên tấm ván đầu tiên. Ở bất kỳ thời điểm nào, hắn ta có thể nhảy lên một tấm ván khác cao hơn nếu những điều kiện sau thỏa mãn:
Tấm ván đó được lắp đặt lên bức tường phía đối diện.
Bạn có thể vẽ một đoạn thẳng từ một điểm bất kỳ trên tấm ván đang đứng, đến điểm xa nhất (so với bức tường mà nó được gắn lên) trên tấm ván mục tiêu, mà không bị cản trở bởi bất kỳ tấm ván nào khác.
Để ra được khỏi hang, Piccôlô cần phải đáp được lên tấm ván cao nhất trên hành trình. Hãy in ra số bước ít nhất Piccôlô cần để làm được điều này. Nếu tấm ván cao nhất không thể đáp tới được với mọi cách đi, in ra -1.
Input
Dòng đầu chứa hai số nguyên: ~N~ và ~W~ (~2 \le N \le 3000~, ~2 \le W \le 10^9~) - thể hiện số tấm ván Piccôlô có thể sử dụng, và khoảng cách giữa hai bức tường.
Dòng thứ hai chứa ~N~ số nguyên: ~h_1, h_2, \ldots, h_N~ (~1 \le h_1 < h_2 < \ldots < h_N \le 10^9~), thể hiện độ cao của từng tấm ván.
Dòng thứ ba chứa ~N~ số nguyên: ~a_1, a_2, \ldots, a_n~ (~1 \le a_1, a_2, \ldots, a_N \le \lfloor\frac{W}{2}\rfloor~), thể hiện độ dài của từng tấm ván.
Dòng thứ tư chứa ~N~ ký tự, cách nhau bởi các dấu cách. Ký tự thứ ~i~ (~1 \le i \le N~) có thể là 'L' hoặc 'R', thể hiện bức tường mà tấm ván thứ ~i~ được lắp lên.
Output
In ra -1 nếu Piccôlô không thể nhảy lên tấm ván cao nhất, tức là tấm ván thứ ~N~.
Ngược lại, in ra số bước ít nhất Piccôlô có thể nhảy để thoát khỏi hang.
Sample Input 1
3 2
1 2 3
1 1 1
L R L
Sample Output 1
2
Sample Input 2
7 7
1 3 4 5 6 7 9
1 1 3 2 3 3 2
R L R L L R L
Sample Output 2
3
Sample Input 3
3 20
1 2 3
10 9 1
L R R
Sample Output 3
1
Notes
Đối với test ví dụ đầu tiên, Piccôlô cần nhảy hai lần như trong hình dưới đây:
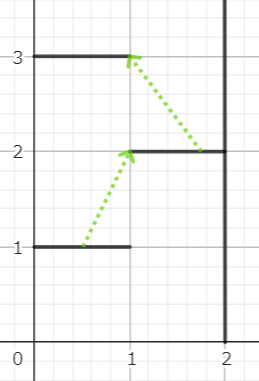
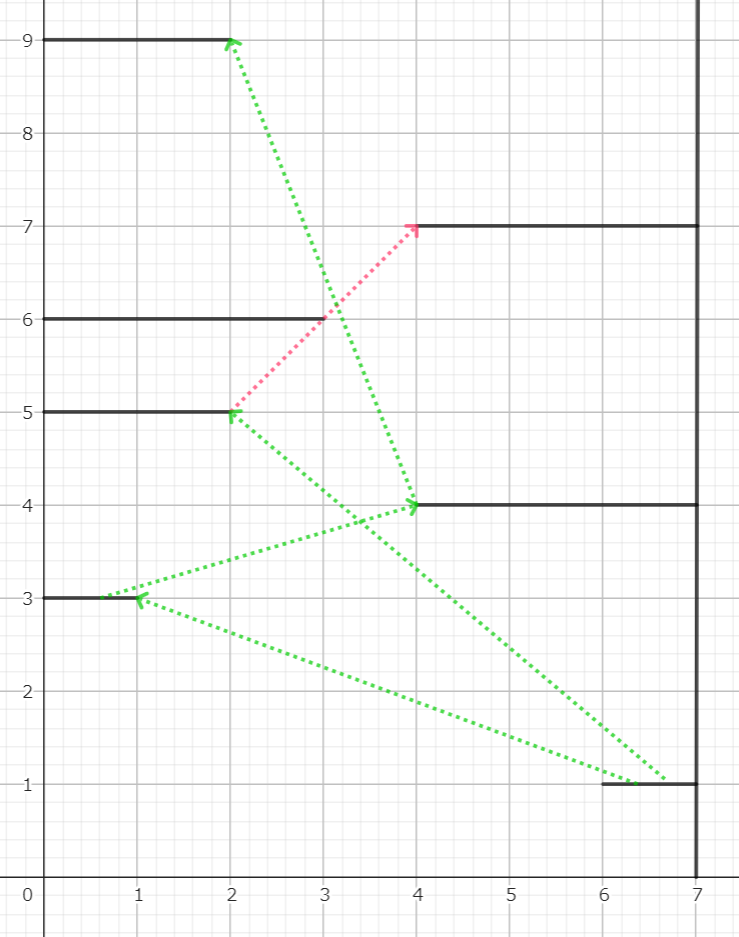
Đối với test ví dụ thứ hai, Piccôlô cần nhảy ba lần lên các tấm ván thứ 2, 3 và 7 như trong hình dưới đây. Ngoài ra, Piccôlô cũng có thể nhảy lên tấm ván thứ 4 từ lần nhảy đầu tiên, nhưng sau đó không thể nhảy lên tấm ván thứ 6 vì bị chặn lại bởi tấm ván thứ 5.
Điểm: 1
| Trong Bảy Viên Ngọc Rồng, hợp thể là cách hai đấu sĩ có thể cùng tạo nên một thực thể, mạnh hơn tổng sức mạnh của cả hai, nhằm mục đích dành chiến thắng trong một trận đấu. Một hợp thể có thể mạnh hơn tổng sức mạnh của hai đấu sĩ, nhưng cũng có thể yếu hơn, tùy vào độ xung-khắc giữa bộ sức mạnh của cả hai. Trong bài toán này, ta sẽ tìm hiểu cách tính sức mạnh hợp thể của hai đấu sĩ, biết chỉ số bộ sức mạnh của họ. |  |
Mỗi đấu sĩ sẽ có một bộ gồm ~N~ chỉ số sức mạnh. Giả sử có đấu sĩ ~A~, với bộ chỉ số là ~A_1, A_2, \ldots, A_N~, và đấu sĩ ~B~, với bộ chỉ số là ~B_1, B_2, \ldots, B_N~, sức mạnh của hợp thể hai đấu sĩ sẽ là chỉ số ~K_{max}~ được tính như sau:
Xét tất cả các số nguyên dương ~M \ge 2~. Với mỗi ~M~, ta tìm ~K_M~, tương đương với đoạn chỉ số ~[l; r]~ (~1 \le l \le r \le N~) dài nhất thỏa mãn:
~A_l \equiv B_l (\mod M)~
~A_{l + 1} \equiv B_{l + 1} (\mod M)~
~A_{l + 2} \equiv B_{l + 2} (\mod M)~
~\ldots~
~A_{r - 1} \equiv B_{r - 1} (\mod M)~
~A_{r} \equiv B_{r} (\mod M)~
Từ đó, ta tính được ~K_{max}~ chính là giá trị ~K_M~ lớn nhất tìm được.
Cho bộ chỉ số sức mạnh của Piccôlô là ~P~, và bộ chỉ số sức mạnh của Goku là ~G~. Hãy tính sức mạnh ~K_{max}~ của hợp thể giữa Piccôlô và Goku. Bạn cũng phải in ra ~M~ lớn nhất tương ứng với ~K_{max}~ bạn tìm được.
Nếu không tính được ~K_{max}~ nào, chứng tỏ hai đấu sĩ không thể hợp thể với nhau: in ra -1.
Nếu ~M~ có thể lên tới vô hạn, chứng tỏ hai đấu sĩ phối hợp vô cùng ăn ý, ta in ra ~0~ cho giá trị của ~M~.
Input
Dòng đầu tiên chứa ~T~ (~1 \le T \le 100~) - số test trong một tệp đầu vào. Mỗi test sẽ có định dạng như sau:
Dòng đầu tiên chứa ~N~ (~1 \le N \le 10^5~) - số phần tử ở cả hai dãy.
Dòng thứ hai chứa ~P_1, P_2, \ldots, P_N~ (~1 \le P_i \le 10^9~), bộ chỉ số sức mạnh của Piccôlô.
Dòng thứ ba chứa ~G_1, G_2, \ldots, G_N~ (~1 \le G_i \le 10^9~), bộ chỉ số sức mạnh của Goku.
Dữ liệu đảm bảo tổng của ~N~ trong tất cả các test sẽ không vượt quá ~5 * 10^5~.
Output
Với mỗi bộ test:
In ra -1 nếu không tìm được ~M~ nào thỏa mãn.
Ngược lại, in ra hai số ~K_{max}~ và ~M~ theo thứ tự, trên cùng một dòng, và cách nhau bởi một dấu cách. Hai số này tương ứng với độ dài dãy con lớn nhất bạn tìm được, và ước chung lớn nhất của nó.
Nếu ~M~ tiến đến vô cùng, ta in ra ~0~ cho giá trị của ~M~.
Sample Input 1
4
8
8 14 5 17 23 6 10 13
6 10 11 8 26 18 18 9
9
8 14 5 17 23 6 10 13 1
6 10 11 8 26 18 18 9 21
3
1 3 5
2 4 6
5
3 4 6 7 2
3 4 6 7 2
Sample Output 1
4 3
4 4
-1
5 0
Notes
Ở bộ test ví dụ đầu tiên: dãy dài nhất tìm được là ~[2; 5]~ (~0~-indexed):
~5 \equiv 11 (\mod 3)~
~17 \equiv 8 (\mod 3)~
~23 \equiv 26 (\mod 3)~
~6 \equiv 18 (\mod 3)~
Ở bộ test ví dụ thứ hai, mặc dù nếu ta chọn ~M = 2~ hay ~M = 3~, cũng thỏa mãn tìm được ~K_M~ lớn nhất. Tuy vậy, ta phải in ra ~M = 4~ vì đề bài yêu cầu ~M~ lớn nhất có thể.
Ở bộ test ví dụ thứ ba, ta không tìm được bất kỳ ~M > 1~ nào mà thỏa mãn tồn tại ~i~ sao cho ~A_i \equiv B_i (\mod M)~.
Điểm: 1
| "Arrgh, hắn lại né được chiêu thức của ta. Giờ là lúc ta phải chạy trốn!" - Frieza thốt lên trong sự bất lực. Hắn ta phải sử dụng phép thuật, thay đổi địa hình của sàn đấu và chạy trốn, trong lúc chờ cho Mana hồi phục. Hắn ta đủ nhanh, để niệm chú phép thuật này trước khi Piccôlô kịp làm gì. |  |
Sàn đấu có ~N~ địa hình. Địa hình thứ ~i~ có độ cao là ~i~. Có ~N-1~ đường đi giữa các địa hình, sao cho giữa hai địa hình luôn có đường đi. Ban đầu, Piccôlô đứng ở địa hình thứ ~1~.
Sau một lần niệm phép thuật của Frieza, độ cao của các địa hình được thay đổi. Tuy vậy, với mọi ~h~ từ ~1~ đến ~N~, luôn tìm được một địa hình có độ cao là ~h~.
Điểm độ khó của sàn đấu mới sẽ tương ứng với số đường đi từ vị trí của Piccôlô đến một nút khác, mà độ cao của từng nút trên đường đi đó tạo ra một dãy tăng dần. Lưu ý rằng, độ cao của địa hình Piccôlô đang đứng trên cũng có thể thay đổi sau lần niệm phép của Frieza, và tất cả các đường đi đều sẽ không thay đổi các địa hình liên kết với chúng.
Hãy tính tổng độ khó của tất cả các sàn đấu mà Frieza có thể tạo ra nếu hắn tuân thủ quy tắc của phép thuật trên. Có ~N!~ cách cho hắn thay đổi nó. In ra kết quả modulo ~10^9+7~.
Input
Dòng đầu chứa ~T~ (~1 \le T \le 1000~) - số test trong một file input. Mỗi test sẽ có format như sau:
Dòng đầu chứa ~N~ (~2 \le N \le 2 * 10^5~) - số địa hình trẻn sàn đấu.
~N - 1~ dòng tiếp theo, mỗi dòng chứa hai số ~u, v~, thể hiện có đường đi giữa hai địa hình ~u~ và ~v~.
Dữ liệu đảm bảo mỗi test sẽ tạo nên một đồ thị dạng cây, và tổng của ~N~ không vượt quá ~5 * 10^5~.
Output
In ra kết quả là một số nguyên trên một dòng duy nhất, modulo ~10^9 + 7~.
Sample Input 1
4
4
1 2
2 3
2 4
4
1 2
2 3
3 4
4
1 2
2 3
1 4
4
1 2
1 3
1 4
Sample Output 1
44
41
52
60
Notes
Để mô tả về cách tính điểm độ khó, chúng tôi sẽ lấy ví dụ về một số hoán vị cho một số cây trong test mẫu.
Chẳng hạn, ở test thứ nhất, đây là một hoán vị:
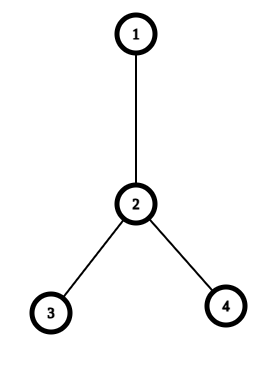
Ở cây này, có ~4~ đường đi tìm được: ~1~, ~1 \rightarrow 2~, ~1 \rightarrow 2 \rightarrow 3~ và ~1 \rightarrow 2 \rightarrow 4~.
Ở test thứ hai, đây là một hoán vị:
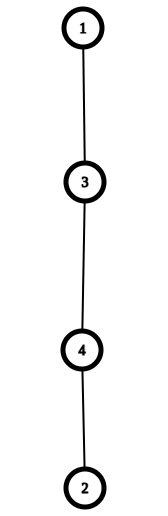
Ở cây này, có ~3~ đường đi tìm được: ~1~, ~1 \rightarrow 3~, và ~1 \rightarrow 3 \rightarrow 4~. Đường đi ~1 \rightarrow 3 \rightarrow 4 \rightarrow 2~ sẽ không được tính vì ~[1, 3, 4, 2]~ không phải dãy tăng dần.
Ở test thứ ba, đây là một hoán vị:
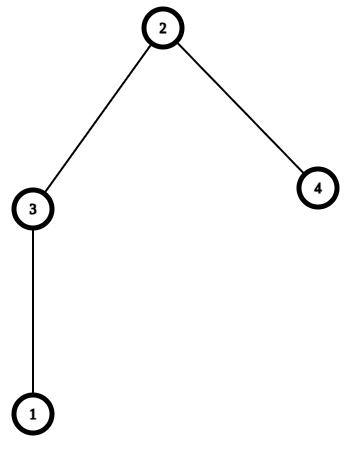
Ở cây này, có ~3~ đường đi tìm được: ~2~, ~2 \rightarrow 3~, ~2 \rightarrow 4~.
Điểm: 1
 |
"Một đấu sĩ khỏe không phải là một đấu sĩ có công lực mạnh nhất. Một đấu sĩ cũng phải có kỹ năng phòng ngự tốt, và phải có khả năng lì đòn để có thể sống sót trước mọi cú đánh hiểm của đối phương. Một bộ lạc tốt cũng vậy: cần phải có một thành trì đủ vững chãi để người dân có thể cư trú, các đấu sĩ có thể yên tâm tập luyện, hồi phục, để trở nên mạnh mẽ nhất trong các trận đấu." |
Piccôlô cần xây dựng một Vòm Phòng ngự cho bộ lạc của mình. Vòm Phòng ngự này sẽ phải chống chọi bất kỳ cuộc tấn công nào của các bộ lạc khác.
Mỗi cuộc tấn công chỉ có thể là một hoán vị của các số từ ~1~ đến ~N~. Sức chịu đựng của Vòm Phòng ngự này sẽ được thể hiện bằng một tập hợp ~K~ hoán vị khác nhau của các số từ ~1~ đến ~N~. ~K~ hoán vị này sẽ là ~K~ hoán vị mà Piccôlô phải chọn, sao cho Vòm Phòng ngự có thể thủ được nhiều cuộc tấn công nhất.
Vòm Phòng ngự có thể thủ được một cuộc tấn công ~P~, nếu như ta tìm được một hoán vị ~Q~ trong tập hợp hoán vị của Vòm Phòng ngự, thỏa mãn: tồn tại một vị trí ~i~ (~1 \le i \le N~) nào đó, sao cho ~P_i = Q_i~. Sau khi thủ thành công một cuộc tấn công, khả năng phòng thủ của Vòm sẽ không thay đổi.
Có ~N!~ cuộc tấn công có thể xảy ra.
Cho ~N~, ~K~, hãy giúp Piccôlô xây dựng một tập hợp các hoán vị: ~Q_1, Q_2, \ldots, Q_K~, sao cho Vòm Phòng ngự tương ứng với tập hợp này có thể thủ được tất cả các cuộc tấn công có thể xảy ra, hoặc chỉ ra không thể xây dựng được tập hợp đó. Bài toán có thể có nhiều đáp án, hãy in ra một đáp số bất kỳ.
Input
Dòng đầu tiên chứa ~T~ (~1 \le T \le 100~) - số test trong một tệp đầu vào. Mỗi test sẽ có định dạng như sau:
- Một dòng duy nhất chứa hai số ~N~ và ~K~ (~1 \le N, K \le 200~).
Output
Với mỗi test:
In ra "NO" trên một dòng nếu không thể tìm được.
Còn lại, in ra "YES", sau đó là mỗi dòng. Dòng thứ ~i~, in ra ~N~ số của hoán vị ~Q_i~ bạn chọn, mỗi số nguyên cách nhau một dấu cách.
Sample Input 1
3
3 2
5 2
6 7
Sample Output 1
YES
1 2 3
1 3 2
NO
YES
1 2 3 4 5 6
2 1 3 4 5 6
2 3 1 4 5 6
2 3 4 1 5 6
2 3 4 5 1 6
2 3 4 5 6 1
1 2 3 4 5 6
Notes
Ở test đầu tiên, tất cả các hoán vị từ ~1~ đến ~3~ sẽ được liệt kê dưới đây:
~1, 2, 3~, được bảo vệ bởi hoán vị ~1~.
~1, 3, 2~, được bảo vệ bởi hoán vị ~1~.
~2, 1, 3~, được bảo vệ bởi hoán vị ~1~.
~2, 3, 1~, được bảo vệ bởi hoán vị ~2~.
~3, 1, 2~, được bảo vệ bởi hoán vị ~2~.
~3, 2, 1~, được bảo vệ bởi hoán vị ~1~.
Ở test thứ ba, ta thấy, tất cả hoán vị độ dài ~6~ đều chứa phần tử ~1~. Và với bất kỳ vị trí nào của phần tử ~1~ trong mọi hoán vị độ dài ~6~, ta đều có thể tìm được một hoán vị trong ~6~ hoán vị đầu tiên ở kết quả mà phòng ngự được hoán vị này.
Điểm: 1
 |
Là hình mẫu truyền cảm hứng cho bao nhiêu thế hệ đấu sĩ kế cận (xong vẫn vả chúng trên sàn đấu như thường), Piccôlô được vinh danh như một đấu sĩ Huyền Thoại trên đấu trường. Một kỷ niệm chương có hình một cái cây trông hơi giống Piccôlô đã được điêu khắc lên, và sử dụng để vinh danh các đấu sĩ xuất sắc nhất trong các năm tiếp theo. |
Ta có thể biểu diễn kỷ niệm chương Piccôlô thành một đồ thị dạng cây gồm ~N~ đỉnh. Trên mỗi đỉnh được gán cho một giá trị ~c_j~, tương ứng với số hiệu của đấu sĩ vô địch giải đấu vào năm thứ ~j~ sau Công Nguyên.
Sau một buổi họp để cải thiện chất lượng tổ chức của các giải đấu cấp dải ngân hà, các hành tinh và bộ tộc đã thống nhất chọn hành tinh chủ nhà cho ~Q~ năm tiếp theo như sau:
Tính từ năm hiện tại, vào năm thứ ~i~, ta sẽ loại bỏ cạnh ~id_i~ trên "cây kỷ niệm chương Piccôlô" (theo danh sách cạnh cho sẵn.
Trong hai cây được tạo bởi ~N - 2~ cạnh còn lại, với mỗi cây, ta sẽ đếm xem có bao nhiêu đỉnh có giá trị chia hết cho ~k_i~.
Số hiệu đại diện cho nước chủ nhà cho giải đấu vào năm thứ ~i~ sẽ là kết quả lớn nhất trong hai số tìm được ở bước trước đó.
Rõ ràng, với một kỷ niệm chương đồ sộ như vậy, thật khó để các nhà tổ chức có thể tự tính toán được bằng tay. Chính vì vậy, bạn hãy giúp họ tính ra danh sách các hành tinh chủ nhà trong những năm tiếp theo nhé!
Input
Dòng đầu chứa ~T~ (~1 \le T \le 1000~) - số test trong một file input. Mỗi test sẽ có format như sau:
Dòng đầu chứa ~N~ (~1 \le N \le 2 * 10^5~) - số đỉnh trên cây.
Dòng tiếp theo gồm ~N~ số: ~c_1, c_2, \ldots, c_N~ (~1 \le c_j \le 10^5~). ~c_j~ thể hiện số hiệu được ghi trên đỉnh thứ ~j~ trên cây.
~N - 1~ dòng sau, dòng thứ ~i~ chứa hai số nguyên ~u_i, v_i~, thể hiện rằng cạnh thứ ~i~ trong danh sách nối giữa ~u_i~ and ~v_i~.
Dòng tiếp theo chứa một số ~Q~ (~1 \le Q \le 2 * 10^5~) - số năm bạn phải tính ra hành tinh chủ nhà.
~Q~ dòng sau, dòng thứ ~i~ chứa hai số nguyên ~id_i~ và ~k_i~ (~1 \le id_i \le N-1~ và ~1 \le k_i \le 10^5~), thể hiện một truy vấn.
Bộ test đảm bảo rằng dữ liệu đồ thị có dạng cây và tổng ~N~ và ~Q~ không vượt quá ~2 * 10^5~
Output
Mỗi bộ test, in ra ~Q~ dòng, mỗi dòng chứa một số nguyên duy nhất là chỉ số của hành tinh chủ nhà, được tính theo thuật toán đã nêu ra ở đề bài.
Sample Input 1
2
8
1 9 1 12 6 2 3 4
1 2
2 3
1 4
2 5
4 6
5 7
2 8
2
1 2
4 3
7
12 80 36 42 30 8 13
1 2
2 3
2 4
2 6
2 7
1 5
4
2 2
5 13
6 3
2 29
Sample Output 1
2
2
5
1
3
0
Notes
Dưới đây là cây Piccôlô đại diện cho bộ test đầu tiên. Các số ghi trên cạnh là chỉ số tương ứng của cạnh đó theo danh sách cho trước:

Điểm: 1
| Sau nhiều năm chiến đấu, bảo về bộ lạc, săn lùng kẻ ác, Piccôlô giờ đảm nhiệm vai trò "trông trẻ". Hắn nhận đào tạo Son Gohan, và có rất nhiều thời gian trong tay để làm những điều hắn muốn. Một trong số đó là chơi TETRIS. |  |
Trò chơi TETRIS có bảy loại khối hình, hay còn gọi là Tetromino: I (thẳng đứng), J, L, O (vuông), S, T, Z; mỗi khối hình bao gồm 4 viên gạch. Ta cần phải thả các khối hình, tương ứng với bảy loại này vào một bảng vuông có độ rộng là ~W~.
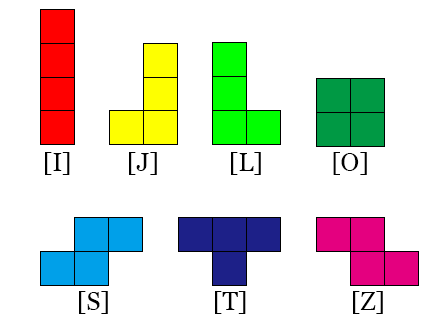
Khi bắt đầu một vòng chơi mới, tetromino đầu tiên sẽ rơi từ trên cùng của màn hình xuống phía dưới. Người chơi có thể di chuyển, xoay và thả nó để tạo ra các hàng hoặc cột hoàn chỉnh để ghi điểm và giải phóng không gian. Một tetromino mới sẽ được trò chơi sinh ra ~1~ trong ~7~ loại trên, nó thể được xoay 0 độ, 90 độ, 180 độ, hoặc 270 độ. Nó sẽ dừng lại khi một trong bốn ô của tetromino gặp phải vật cản trên cùng cột với nó. Khi đó, tetromino giữ vị trí cố định, và tetromino mới bắt đầu rơi xuống. Nếu sau khi một tetromino được giữ cố định, mà tạo ra một số hàng được lấp đầy bởi các viên tetromino, hàng đó sẽ biến mất, và người chơi được cộng điểm.
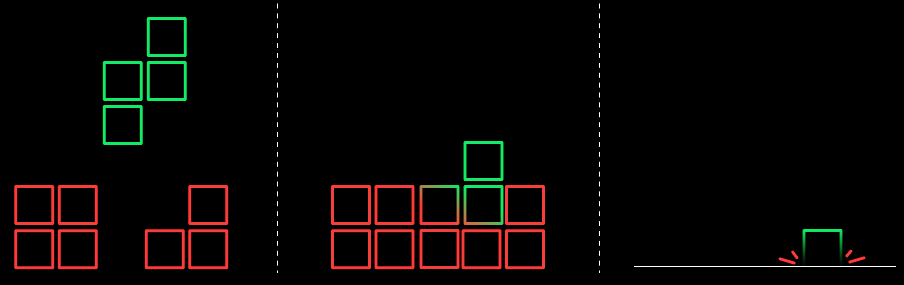
Piccôlô chơi Tetris, và bạn có danh sách nước đi của hắn ta. Mỗi nước đi sẽ được thể hiện qua ba dữ kiện:
~s_i~ là một trong bảy ký tự: 'I', 'J', 'L', 'O', 'S', 'T', 'Z', thể hiện hình dạng của Tetromino rơi xuống ở nước đi này.
~r_i~ thể hiện góc quay của viên gạch, theo chiều kim đồng hồ. Giá trị này có thể là một trong bốn số: ~0~, ~90~, ~180~, ~270~.
~c_i~ thể hiện chỉ số cột mà Tetromino này sẽ rơi xuống. Cụ thể, chỉ số này là cột mà ô ngoài cùng bên trái của Tetromino sẽ rơi xuống.
Ngoài ra, hắn còn một nước đi đặc biệt: khôi phục trò chơi về trước nước đi thứ ~i~ nào đó. Hắn có thể làm thế tùy thích, chẳng hạn nếu như cảm thấy mình có thể có nước đi tốt hơn có thể đi lại từ nước đi này. Đồng thời, khác với chế độ TETRIS cơ bản, hắn có thể để cho các tetromino của mình lên độ cao tùy ý mà không bị thua (chiều cao của bảng là vô hạn).
Nhiệm vụ của bạn, sau mỗi nước đi của Piccôlô, hãy in ra độ cao của hàng lớn nhất, mà xuất hiện một phần của một Tetromino.
Input
Dòng đầu chứa hai số nguyên ~W~ (~1 \leq W \leq 10000~) và ~N~ (~1 \leq N \leq 50000~) lần lượt là chiều rộng của bảng chơi và số lượt chơi.
~N~ dòng tiếp theo, mỗi dòng mô tả 1 lượt chơi.
Piccôlô có thể thực hiện nước đi thứ ~i~ là thả viên gạch mới. Khi đó, nước đi này sẽ có dạng: "~s_i\ r_i \ c_i~" (~r_i \in \{0, 90, 180, 270\}~, ~0 \leq c_i \lt W~), lần lượt thể hiện hình dạng, chiều quay, và chỉ số cột của viên gạch này.
Piccôlô có thể thực hiện nước đi thứ ~i~ là khôi phục lại về nước đi ~m_i~ nào đó. Khi đó, nước đi này sẽ có dạng "~.\ m_i~", ~m_i~ thể hiện chỉ số của nước đi mà Piccôlô có thể khôi phục về.
Output
- Tương ứng với mỗi lượt chơi, in ra trên một dòng độ cao của viên gạch cao nhất đang tồn tại trong bảng.
Sample Input 1
5 11
I 90 0
J 270 2
L 270 2
T 90 0
Z 90 0
O 180 2
S 90 3
. 5
J 90 2
. 0
T 180 1
Sample Output 1
1
1
3
2
4
3
3
4
3
0
2
Notes
Với test ví dụ, trạng thái của bảng sau các lượt chơi như sau:
1)
****.
2)
..***
3)
....*
..***
..***
4)
.*..*
.****
5)
.*...
**...
**..*
.****
6)
.*...
****.
.****
7)
...*.
.*.**
.****
8)
.*...
**...
**..*
.****
9)
.**..
**..*
.****
10)
.....
11)
..*..
.***.