Piccôlô và Phép Thuật của Frieza
Xem dạng PDF| "Arrgh, hắn lại né được chiêu thức của ta. Giờ là lúc ta phải chạy trốn!" - Frieza thốt lên trong sự bất lực. Hắn ta phải sử dụng phép thuật, thay đổi địa hình của sàn đấu và chạy trốn, trong lúc chờ cho Mana hồi phục. Hắn ta đủ nhanh, để niệm chú phép thuật này trước khi Piccôlô kịp làm gì. |  |
Sàn đấu có ~N~ địa hình. Địa hình thứ ~i~ có độ cao là ~i~. Có ~N-1~ đường đi giữa các địa hình, sao cho giữa hai địa hình luôn có đường đi. Ban đầu, Piccôlô đứng ở địa hình thứ ~1~.
Sau một lần niệm phép thuật của Frieza, độ cao của các địa hình được thay đổi. Tuy vậy, với mọi ~h~ từ ~1~ đến ~N~, luôn tìm được một địa hình có độ cao là ~h~.
Điểm độ khó của sàn đấu mới sẽ tương ứng với số đường đi từ vị trí của Piccôlô đến một nút khác, mà độ cao của từng nút trên đường đi đó tạo ra một dãy tăng dần. Lưu ý rằng, độ cao của địa hình Piccôlô đang đứng trên cũng có thể thay đổi sau lần niệm phép của Frieza, và tất cả các đường đi đều sẽ không thay đổi các địa hình liên kết với chúng.
Hãy tính tổng độ khó của tất cả các sàn đấu mà Frieza có thể tạo ra nếu hắn tuân thủ quy tắc của phép thuật trên. Có ~N!~ cách cho hắn thay đổi nó. In ra kết quả modulo ~10^9+7~.
Input
Dòng đầu chứa ~T~ (~1 \le T \le 1000~) - số test trong một file input. Mỗi test sẽ có format như sau:
Dòng đầu chứa ~N~ (~2 \le N \le 2 * 10^5~) - số địa hình trẻn sàn đấu.
~N - 1~ dòng tiếp theo, mỗi dòng chứa hai số ~u, v~, thể hiện có đường đi giữa hai địa hình ~u~ và ~v~.
Dữ liệu đảm bảo mỗi test sẽ tạo nên một đồ thị dạng cây, và tổng của ~N~ không vượt quá ~5 * 10^5~.
Output
In ra kết quả là một số nguyên trên một dòng duy nhất, modulo ~10^9 + 7~.
Sample Input 1
4
4
1 2
2 3
2 4
4
1 2
2 3
3 4
4
1 2
2 3
1 4
4
1 2
1 3
1 4
Sample Output 1
44
41
52
60
Notes
Để mô tả về cách tính điểm độ khó, chúng tôi sẽ lấy ví dụ về một số hoán vị cho một số cây trong test mẫu.
Chẳng hạn, ở test thứ nhất, đây là một hoán vị:
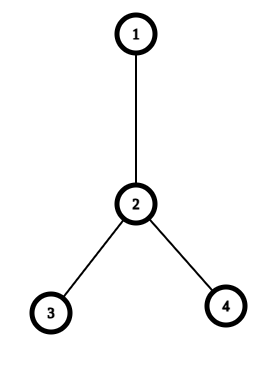
Ở cây này, có ~4~ đường đi tìm được: ~1~, ~1 \rightarrow 2~, ~1 \rightarrow 2 \rightarrow 3~ và ~1 \rightarrow 2 \rightarrow 4~.
Ở test thứ hai, đây là một hoán vị:
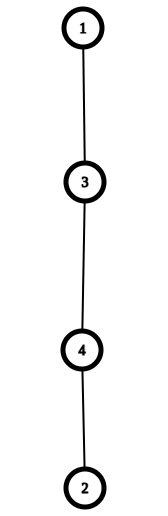
Ở cây này, có ~3~ đường đi tìm được: ~1~, ~1 \rightarrow 3~, và ~1 \rightarrow 3 \rightarrow 4~. Đường đi ~1 \rightarrow 3 \rightarrow 4 \rightarrow 2~ sẽ không được tính vì ~[1, 3, 4, 2]~ không phải dãy tăng dần.
Ở test thứ ba, đây là một hoán vị:
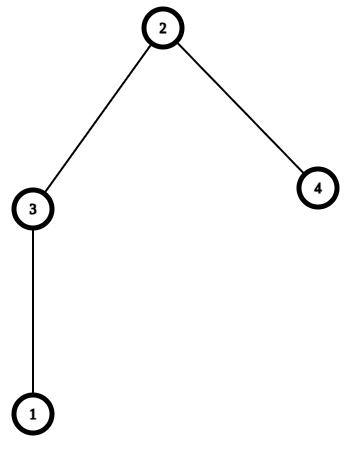
Ở cây này, có ~3~ đường đi tìm được: ~2~, ~2 \rightarrow 3~, ~2 \rightarrow 4~.
Bình luận