Chung, the self-proclaimed "Grand Alchemist," has returned to challenge the talents of BKCC#3. This time, he has unearthed a row of ancient mana stones, but he lacks the magical prowess to stabilize their volatile energy.

He has arranged ~n~ crystals in a sequence, where the ~i~-th crystal possesses a power level of ~a_i~. A "Fusion" is created by combining the power of a contiguous sequence of crystals. If we select crystals from index ~l~ to ~r~, the total energy ~X~ is the product of their individual powers: $$X = a_l \times a_{l+1} \times \cdots \times a_r$$

However, a Fusion is unstable in its raw form. To stabilize it, the total energy ~X~ must be partitioned into two distinct components, positive values ~A~ and ~B~, such that:

• The product restores the total energy: ~A \times B = X~.

• The components are structurally distinct: ~A < B~.

• The components share no common resonance: ~A~ and ~B~ are coprime (i.e., ~\gcd(A, B) = 1~).

Chung defines the stability function ~f(X)~ as the number of valid ways to partition the energy ~X~ according to these rules.

To prove your mastery over the arcane arts, you must calculate the Grand Resonance S, defined as product of ~f(X)~ for every possible contiguous sub-segment of the crystal sequence modulo ~10^9 + 7~. Formally:

$$S = \prod_{1 \le l \le r \le n}{f(a_l \times a_{l+1} \times \cdots \times a_{r-1} \times a_r)} \mod 10^9 + 7$$

Input

The first line contains a positive integer ~T~ — the number of test cases.

Each test case is described as follows:

• The first line contains a positive integer ~n~ (~n \le 2 \times 10^5~).

• The next line contains ~n~ positive integers ~a_1, a_2, \cdots, a_n~ (~2 \le a_i \le 10^6~).

The data guarantees that the total ~n~ across all test cases does not exceed ~2 \times 10^5~.

Output

For each test case, print an integer — the value of ~S~.

Sample Input 1

3
1
15
3
3 4 5
4
2 2 3 4

Sample Output 1

2
16
32

Notes

In the first test case, ~15~ can only be partitioned as (~1, 15~) and (~3, 5~), so there are ~2~ possible pairs.

In the second test case, consider all segments as follows:

• ~[3] \rightarrow 3 \rightarrow (1,3) \rightarrow~ ~1~ pair

• ~[4] \rightarrow 4 \rightarrow (1,4) \rightarrow~ ~1~ pair

• ~[5] \rightarrow 5 \rightarrow (1,5) \rightarrow~ ~1~ pair

• ~[3,4] \rightarrow 12 \rightarrow (1,12), (3,4) \rightarrow~ ~2~ pairs

• ~[4,5] \rightarrow 20 \rightarrow (1,20), (4,5) \rightarrow~ ~2~ pairs

• ~[3,4,5] \rightarrow 60 \rightarrow (1,60), (4, 15), (3, 20), (5, 12) \rightarrow~ ~4~ pairs

Thus, ~S = 1 \times 1 \times 1 \times 1 \times 2 \times 2 \times 4 = 16~

After saving enough money to retire, Bảo has accumulated a considerable amount and decided to build a new ecological garden. With his rich imagination, Bảo designed the garden to include ~n~ small gardens with the following details:

• Each garden ~i~ is circular and surrounded by a wall. On the wall, there are ~c~ evenly spaced doors. Note: all gardens have the same number of doors.

• For garden ~i~, there are ~m_i~ flower paths (chords). The ~j~-th path of the garden ~i~ connects two doors ~u_j, v_j~ and crosses the internal passage of that garden.

• Tourists who want to go straight from door ~x~ to door ~y~ within the same garden must jump over all the flower paths that intersect the straight line connecting those two doors(refer to the illustration below)

  

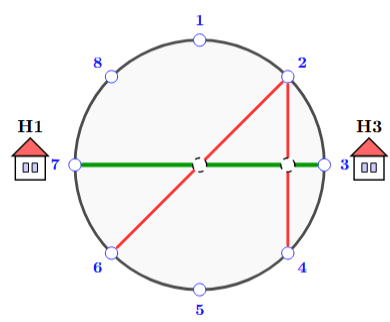
  The visitor's path from door ~7~ to door ~3~, crossing two red flower paths ~(2, 4)~ and ~(2, 6)~

• Outside the wall, the gardens are connected by ~n - 1~ paths. This path system ensures that there is always a way back and forth between any two gardens. The ~k~-th path connects door ~u_k~ of garden ~x_k~ to door ~v_k~ of garden ~y_k~.

• Each door can only be used for one purpose. If a door is connected to an outside path, it cannot be connected to an internal flower path, and vice versa.

Noticing that visitors move with great difficulty in this design, Bảo added ~d~ rest houses scattered throughout the tourist area. The rest houss ~t~ placed right behind door ~u_t~ of any garden ~x_t~. The position of the rest house also follows the above rule: a door that has a rest house cannot be connected to any other path or flower path.

To evaluate the quality of the design, the "inconvenience score" between any two rest houses ~u~ and ~v~ is calculated by the total number of flower paths that need to be jumped over when traveling from one rest house to the other. To assess this comprehensively, Bảo wonders what the total inconvenience score of all pairs of rest houses in this garden is. Please help Bảo!

Input

The first line contains a positive integer ~T~ — the number of test cases.

Each test case is described as follows:

• The first line contains 3 positive integers ~n, d, c~ (~1 \le n, d \le 2 \times 10^5~, ~1 \le c \le 10^9~) — the number of gardens, rest houses, and the number of doors in each garden.

• The next ~n~ groups of the data contain information about each garden:

  • The first line contains a positive integer ~m_i~ (~1 \leq m_i \leq 2 \times 10^5~) — the number of doors and flower paths in the ~i~-th garden.

  • The ~i~-th of the next ~m_i~ lines each contain three positive integers ~u_j, v_j~ (~1 \leq u_j, v_j \leq c~) — a flower path connecting the ~u_j~-th and ~v_j~-th doors.

• The ~k~-th of the next ~n - 1~ lines contain five positive integers ~x_k, u_k, y_k, v_k~ (~1 \leq x_k, y_k \leq n, 1 \leq u_k, v_k \leq c~) — the path connecting door ~u_k~ of garden ~x_k~ to door ~v_k~ of garden ~y_k~.

• The ~t~-th of the last ~d~ lines contain two positive integers ~x_t, u_t~ (~1 \leq x_t \leq n, 1 \leq u_t \leq c~) — the position of the ~t~-th rest house.

• The data guarantees that each door is connected to at most one flower path, outside path, or rest house.

It is guaranteed that across all test cases, the total of ~\sum n~ and ~\sum d~ does not exceed ~2 \times 10^5~ respectively, and the total ~\sum m_i~ does not exceed ~6 \times 10^5~.

Output

For each test case, output a single integer — the total inconvenience score between the rest houses.

Sample Input 1

1
4 3 8
2
2 4
2 6
0
0
1
2 4
1 3 4 1
1 5 2 1
1 7 3 1
2 2
3 2
4 3

Sample Output 1

6

Notes

The image illustrates the example test case.

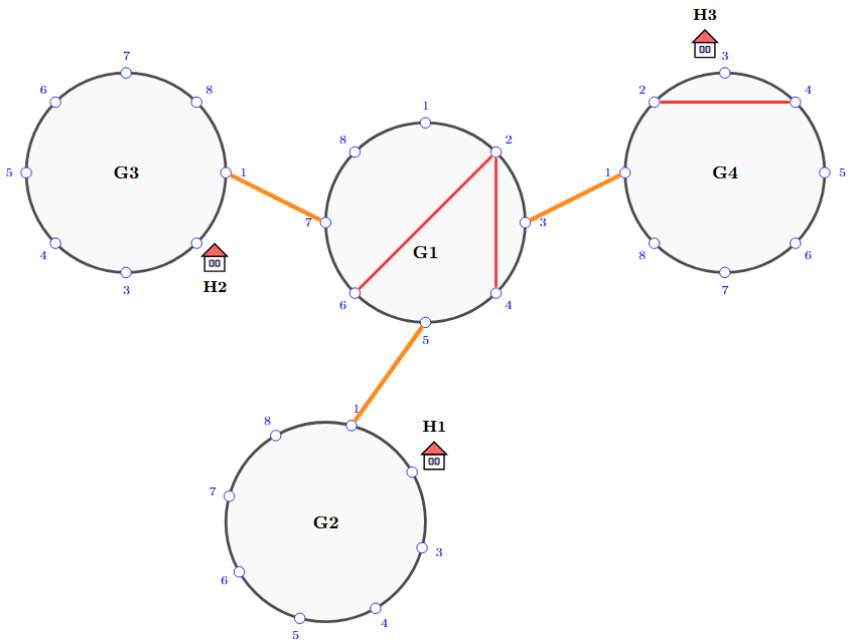
The path between rest house ~1~ and ~2~ passes through ~1~ red path ~(2, 6)~ of garden 1.

The path between rest house ~1~ and ~3~ passes through ~2~ red paths ~(2, 6)~ of garden 1 and ~(2, 4)~ of garden 4.

The path between rest house ~2~ and ~3~ passes through ~3~ red paths ~(2, 6), (2, 4)~ of garden 1 and ~(2, 4)~ of garden 4.

The total score is: ~1 + 2 + 3 = 6~

Santa Claus has gathered ~n~ children sitting in a perfect circle. Each child ~i~ sits between child ~(i-1)~ and child ~(i+1)~, with child ~1~ and child ~n~ also sitting next to each other.

Initially, Santa distributed candies to the children. However, the children have already divided them among themselves in some way, possibly unfairly, and some children may even have none. Watching this, Santa recalls his younger days, when he often shared his candies so generously that he ended up with less or even none. Feeling nostalgic, he decides that every child should have the same number of candies.

To achieve this, Santa may give simple instructions. In each second, he may pick any child who currently has at least ~2~ candies and tell that child to give one candy to each of their two neighboring children. We call an initial distribution of candies fair if there exists a finite sequence of instructions (following the rule above) such that, after performing them, every child has the same number of candies.

However, Santa does not know the number of candies of every child. Some children are already sitting in the circle and truthfully report their number of candies, while the rest are still out playing and have not returned yet, and Santa has no information about their candy counts. He knows that each child has at most ~K~ candies.

Given the reported values for the children already present, Santa wonders: How many possible candies states that is considered fair with the numbers he already knows?

Help Santa compute the number of such fair candies states

Input

The first line contains a positive integer ~T~ (~1 \le T \le 500~) — the number of test cases. Each test case is described as follows:

The first line contains a positive odd integer ~n~ (~3 \le n \le 500~, ~1 \le K \le 10^9~) — the number of children, and the maximum number of candies a child initially has.

The second line contains ~n~ integers ~a_1, a_2, \dots, a_n~ (~-1 \le a_i \le K~), the number of candies that child ~i~ currently has. A value of ~a_i = -1~ means that child ~i~ is still out playing and has not returned to the circle yet, so Santa does not know how many candies they currently hold.

The data guarantees that the total of all values ~n^3~ over all test cases does not exceed ~500^3~.

Output

For each test case, print a single integer — the number of fair initial distributions of candies consistent with the known values, modulo ~10^9 + 7~.

Sample Input 1

2
3 1
1 1 1
3 2
-1 -1 -1

Sample Output 1

1
3

Sample Input 2

2
5 2
2 0 0 2 1
5 2
2 0 0 -1 -1

Sample Output 2

1
1

Notes

In the first example, test case 2, there are three fair initial distributions: ~[0, 0, 0],[1, 1, 1],[2, 2, 2]~.

In the second example, test case 1 is a fair initial distribution. The process to reach every child having one candy can occur in the following order:

• Child number 4 gives one candy to child number 3 and child number 5.

• Child number 5 gives one candy to child number 4 and child number 1.

• Child number 1 gives one candy to child number 2 and child number 5.

Bob is learning a new data normalization technique. He has an array of data values ~A~ of size ~n~, and a list of special prime numbers ~B~ of size ~m~.

For any pair of values ~(x, y)~, the normalized value is calculated using the following algorithm:

def normalize(x, y, B[]):
    while exists p in B such that (x % p == 0) and (y % p == 0):
        x = x / p
        y = y / p
    return x + y

Fascinated by how this technique works, Bob challenges you to calculate the total sum of the normalized values for all possible pairs ~(a_i, a_j)~ where ~1 \le i < j \le n~.

Input

The first line contains two integers ~n~ and ~m~ (~2 \le n \le 5 \cdot 10^5~, ~1 \le m \le 10^5~) — the number of data values and the number of special primes.

The second line contains ~n~ integers ~a_1, a_2, \ldots, a_n~ (~1 \le a_i \le 2\cdot 10^6~) — the data values.

The third line contains ~m~ distinct integers ~b_1, b_2, \ldots, b_m~ (~1 \le b_i \le 2\cdot 10^6~, all ~b_i~ are prime numbers) — the list of special primes.

Output

Print a single integer — the sum of normalized values for all pairs.

Sample Input 1

3 2
3 6 8
2 3

Sample Output 1

21

Sample Input 2

5 2
2 4 6 8 10
2 3

Sample Output 2

57

Notes

In the example above, the set of special primes is ~B = \{2, 3\}~. The pairs are normalized as follows:

• Pair ~(3, 6)~: The common prime factor is ~3~. Since ~3 \in B~, we divide both by 3 to get ~(1, 2)~. Result: ~1 + 2 = 3~.

• Pair ~(3, 8)~: The greatest common divisor is 1. No reduction is performed. Result: ~3 + 8 = 11~.

• Pair ~(6, 8)~: The common prime factor is ~2~. Since ~2 \in B~, we divide both by 2 to get ~(3, 4)~. Result: ~3 + 4 = 7~.

Total sum: ~3 + 11 + 7 = 21~.

The Grand Guild of Arcanum is preparing for a massive expedition into the Void. The Guild Master, Bao, has a list of adventurers categorized into n distinct character classes (such as Paladins, Mages, Rogues, Bards, etc.). The guild registry shows that there are currently ~a_i~​ adventurers available for the ~i~-th class.

To ensure the survival of the expedition teams, the Guild Council has mandated strict formation rules. Every expedition squad must consist of exactly ~k~ adventurers. However, due to clashing magical auras and incompatible fighting styles, a squad cannot contain more than one adventurer of the same class. Furthermore, each adventurer can be assigned to at most one squad.

Bao wants to deploy as many squads as possible to maximize the Guild's presence in the Void. Given the current roster of adventurers and their classes, your task is to calculate the maximum number of full, valid squads Bao can form.

Input

The first line contains a positive integer ~T~ (~1 \le T \le 1000~) — the number of test cases.

The first line of each test case contains two positive integers ~n~ and ~k~ (~1 \le k \le n \le 2 \cdot 10^5~) — the number of character classes and the required size of a squad.

The second line of each test case contains ~n~ integers ~a_1, a_2, \ldots, a_n~ (~0 \le a_i \le 10^9~) — the number of available adventurers of each class.

The total ~n~ across all test cases does not exceed ~2 \cdot 10^5~.

Output

For each test case, print the maximum number of squads that can be formed on a new line.

Sample Input 1

2
4 3
3 2 1 1
4 4
3 2 2 1

Sample Output 1

2
1

Notes

In the first testcase, there can be maximum ~2~ squads. The first squad will have members of class ~1~-th, ~2~-th and ~3~-rd while the second class will have members of the ~1~-st, ~2~-nd and ~4~-th class.

Bao is a pioneer in Precision Agriculture. His massive plantation is mapped onto an ~n \times n~ coordinate grid, where both rows and columns are numbered from ~1~ to ~n~. Rows are counted from top to bottom, and columns from left to right. To monitor crop health, Bao has installed ~m~ Sentinel Towers at fixed coordinates ~(x_i, y_i)~. No two towers occupy the same grid coordinate.

Bao plans to activate a "Protection Shield" over specific square regions of the field. A Protection Shield covers a square sub-grid of size ~k \times k~ with its top-left corner at (~u,v~).

However, the shield technology requires a perfect energy balance to function. A shield covering a specific sub-grid is considered stable only if it satisfies the Singular Projection Rule:

• Row Stability: Every single row intersecting the sub-grid must contain exactly one Sentinel Tower inside the sub-grid.

• Column Stability: Every single column intersecting the sub-grid must contain exactly one Sentinel Tower inside the sub-grid.

Formally, for a shield of size ~k~ with its top-left corner at (~u,v~), the range of rows is [~u,u+k-1~] and the range of columns is [~v,v+k-1~] the property must hold strictly within these bounds.

Bao has ~q~ queries to process. Each query provides a proposed location (~k,u,v~). Your task is to determine whether a shield activated at this location would be stable.

Input

The first line contains a positive integer ~t~ (~1 \le t \le 1000~) — the number of test cases.

The first line of each test case contains two positive integers ~n~ and ~m~ (~1 \le n \le 2 \cdot 10^5~, ~1 \le m \le \mathrm{min}(2 \times 10^5, n^2)~) — the dimensions of the field and the number of Sentinel Towers.

The next ~m~ lines of each test case contain two positive integers ~x~ and ~y~ (~1 \le x, y \le n~) — the coordinates of the rice plants.

The ~m + 2~-th line of each test case contains a positive integer ~q~ (~1 \le q \le 2 \cdot 10^5~) — the number of queries.

The next ~q~ lines of each test case contain three positive integers ~k~, ~u~, ~v~ (~1 \le k \le n~, ~1 \le u, v \le n - k + 1~) — the square sub-grid with a side length of ~k~ with its top-left point located at cell (~u, v~).

The input data guarantees that the total ~q~ does not exceed ~2 \cdot 10^5~. The input data guarantees that the total ~n~ does not exceed ~2 \cdot 10^5~.

Output

For each query, print Yes on a new line if the shield is stable (satisfies the Singular Projection Rule) otherwise, print No.

Sample Input 1

1
5 7
1 4
2 2
3 3
4 2
4 5
5 1
5 4
5
3 2 2
2 3 2
3 3 1
5 1 1
3 3 3

Sample Output 1

No
Yes
Yes
No
Yes

Notes

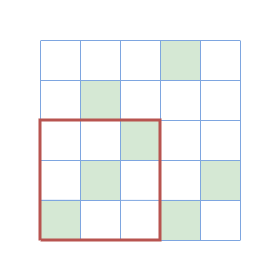
In the first test case, the following figure illustrates the field and the locations of the towers (shown as marked cells):

In the first query, the third column of the subsquare (marked in red) doesn't have a tower.

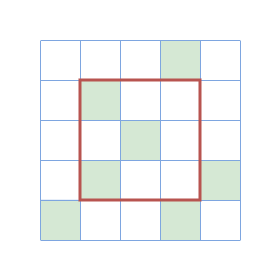
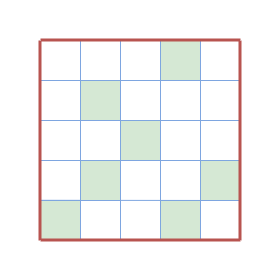
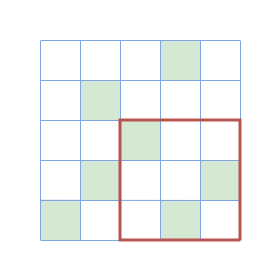
In the second query, the subsquare's shield is stable.

Figures of the 3rd, 4th, and 5th query.

In a classroom, Van and Long are playing a game to determine who is smarter. At the beginning of the game, each person secretly writes down a positive integer: Long writes the number ~A~, while Van writes the number ~B~. Both numbers are then given to Chung, who is the referee of the game.

Chung then writes two numbers, ~X~ and ~Y~, on the blackboard such that at least one of the two numbers is equal to the sum of ~A~ and ~B~, meaning either ~X = A + B~, or ~Y = A + B~, or both.

The game begins. In each round, Chung asks Long: "Do you know Van's number?". If Long answers "No", then Chung asks Van the same question: "Do you know Long's number?". If Van also answers "No", the next round begins, repeating this process. The game continues until one of them answers "Yes", correctly stating the other person's number, and wins the game.

Both Van and Long are very intelligent and only answer "Yes" when they are completely sure of the other person's number. They know other player will do the same and they will play optimally based on all the information they have.

Chung is curious: with the initial numbers ~A~, ~B~, ~X~, and ~Y~ given, who will win the game—or will the game go on forever?

Input

The first line contains an integer ~t~ (~1 \leq t \leq 2 \times 10^5~) — the number of test cases.

Each of the following ~t~ lines contains four integers ~A~, ~B~, ~X~, and ~Y~ (~1 \leq A, B \leq 10^{18}~, ~2 \leq X, Y \leq 2 \times 10^{18}~) — representing the numbers chosen by Long, Van, and the two numbers written by Chung on the blackboard. It is guaranteed that at least one of the two numbers ~X~ or ~Y~ is equal to the sum of ~A~ and ~B~.

Output

For each test case, output the number of rounds in which the game ends and the name of the winner. If neither player can determine the other's number, output "Impossible".

Sample Input 1

2
3 4 7 7
2 10 5 12

Sample Output 1

1 Long
1 Van

Notes

In the first example, since ~X = Y = 7~ and Long's number is ~3~, the only possible value for the number that Van could write to satisfy the condition is ~4~. Therefore, Long can immediately deduce Van's number and win in the first round.

In the second example, in the first round, from Long's perspective, the possible values for ~B~ are ~3~ or ~10~, so Long cannot determine Van's number and must answer "No". As for Van, knowing that his number is ~B = 10~, and since ~10 < 5~ is unreasonable, Van can deduce that Long's number must be ~12 - 10 = 2~ and win in the first round.

Bảo is working on a new "Harmonization Module" for his newly joined company. This module is designed to link old user data with new database entries.

For the system to work, Bảo must find two massive "key" values, ~x~ and ~y~. These keys must be successfully "harmonized" with a special "Legacy Constant" ~A~, a number Bảo is particularly fond of.

According to an old algorithm manual, a pair (~x,y~) is considered harmonized if the following formula produces a positive integer: $$\sqrt{xy+x+A​}$$

The system has strict constraints: both keys ~x~ and ~y~ must be integers between ~1~ and ~10^9~ (inclusive).

Bảo needs to run ~T~ test scenarios, each with a different Legacy Constant ~A~. Your job is to help him find any valid pair ~(x,y)~ that satisfies the harmonization criteria.

Input

The first line contains a single integer ~T~ (~1 \le T \le 10^5~) — the number of test scenarios.

Each of the next ~T~ lines contains a single integer ~A~ (~−10^9 \le A \le 10^9~) — Bảo's favorite number (the Legacy Constant).

Output

For each test scenario, print a single line with two space-separated integers, ~x~ and ~y~, if a valid pair is found. If no such pair exists within the constraints, print ~−1~.

Sample Input 1

4
3
-1
2
-1000000000

Sample Output 1

11 2
10 4
14 6
1000000000 10

Chung is studying sequence partitioning. He learn that a valid partition as a division of a sequence into one or more contiguous segments such that every element belongs to exactly one segment.

Initially, he has a sequence of ~n~ integers. He calls a partition a ~k~-signature partition if every segment in the partition contains at least one occurrence of the integer ~k~.

Mr. K thinks the static problem is too easy, so he challenges Chung to solve the problem dynamically by processing the following queries:

• ~1 \ l \ r \ v~ (~1 \le l \le r \le n, |v| \le 10^5~) — Add the value ~v~ to every element in the range ~[l, r]~. It is guaranteed that after this operation, all elements ~a_i~ in the sequence satisfy ~1 \le a_i \le 10^5~.

• ~2 \ l \ r \ k~ (~1 \le l \le r \le n, 1 \le k \le 10^5~) — Consider only the subarray from index ~l~ to ~r~. Calculate the number of ~k~-signature partitions for this subarray. Since the answer can be large, output it modulo ~10^9 + 7~.

Overwhelmed by the changing array, Chung asks for your help to answer Mr. K's queries!

Input

The first line contains a positive integer ~T~ (~1 \leq T \leq 10^5~) — the number of test cases. Each test case is described as follows:

The first line contains two positive integers ~n, q~ (~1 \leq n, q \leq 10^5~) — the length of the sequence ~a~ and the number of queries you need to process.

The second line contains ~n~ positive integers ~a_i~ (~1 \leq a_i \leq 10^5~) — the values of the elements in the sequence ~a~.

The next ~Q~ lines describe the queries as stated in the problem.

The data guarantees that the total ~n~ and ~q~ will not exceed ~10^5~.

Output

For each query of type ~2~, return the answer. Since the answer may be large, return the result modulo ~10^9 + 7~.

Sample Input 1

1
5 3
1 2 1 3 1
2 1 5 1
1 2 4 2
2 1 4 1

Sample Output 1

9
1

Notes

1. One Segment (1 way)

• | 1 | 2 | 1 | 3 | 1 | |:---:|:---:|:---:|:---:|:---:|

2. Two Segments (4 ways)

• | 1 | 2 | 1 | 3 | 1 | |:---:|:---:|:---:|:---:|:---:|

• | 1 | 2 | 1 | 3 | 1 | |:---:|:---:|:---:|:---:|:---:|

• | 1 | 2 | 1 | 3 | 1 | |:---:|:---:|:---:|:---:|:---:|

• | 1 | 2 | 1 | 3 | 1 | |:---:|:---:|:---:|:---:|:---:|

3. Three Segments (4 ways)

• | 1 | 2 | 1 | 3 | 1 | |:---:|:---:|:---:|:---:|:---:|

• | 1 | 2 | 1 | 3 | 1 | |:---:|:---:|:---:|:---:|:---:|

• | 1 | 2 | 1 | 3 | 1 | |:---:|:---:|:---:|:---:|:---:|

• | 1 | 2 | 1 | 3 | 1 | |:---:|:---:|:---:|:---:|:---:|

Recently, at the center of the Chess Kingdom, a king has created a challenge for his bravest knights. In the large courtyard is a square gemstone floor of size ~n \times n~, divided into small squares. Each square can either contain a mysterious black crystal (denoted as #) — a material that can absorb all sunlight, or a transparent square (denoted as .).

The knights stand in turn at the four walls of the courtyard: North, South, West, or East, holding the legendary Prism of Illumination. By adjusting the prism, the knight can project a beam of parallel light perpendicular to the walls:

• From the North wall, the beams shine down each column towards the South.

• From the South wall, the beams shoot up each column towards the North.

• From the West wall, the beams sweep across each row towards the East.

• From the East wall, the beams sweep across each row towards the West.

When a beam encounters at least one crystal (~\#~) on its path, it creates a shadow projected onto the opposite wall at the corresponding column position (for North/South) or row (for West/East). The knight records a shadow for that position. If no crystal is encountered, that position remains brightly lit.

Legend has it that the winning knight will be the one who finds the "brightest" viewpoint — meaning the direction to shoot the beam where the number of shaded positions is minimal.

Input

The first line contains a positive integer ~T~ (~1 \le T \le 100~) — the number of test cases.

The first line of each test case contains a positive integer ~n~ (~1 \le n \le 100~) — the size of the gemstone floor.

The next ~n~ lines of each test case consist of a string of length ~n~ made up of two characters (~\#~ or ~.~) — the squares of the gemstone floor.

Output

For each test case, print on one line the minimum number of shaded positions.

Sample Input 1

2
3
###
#.#
...
4
#...
.#..
..#.
...#

Sample Output 1

2
4

Notes

In the first example, if The knights shoots the beam from the West, the number of shaded positions is ~2~.

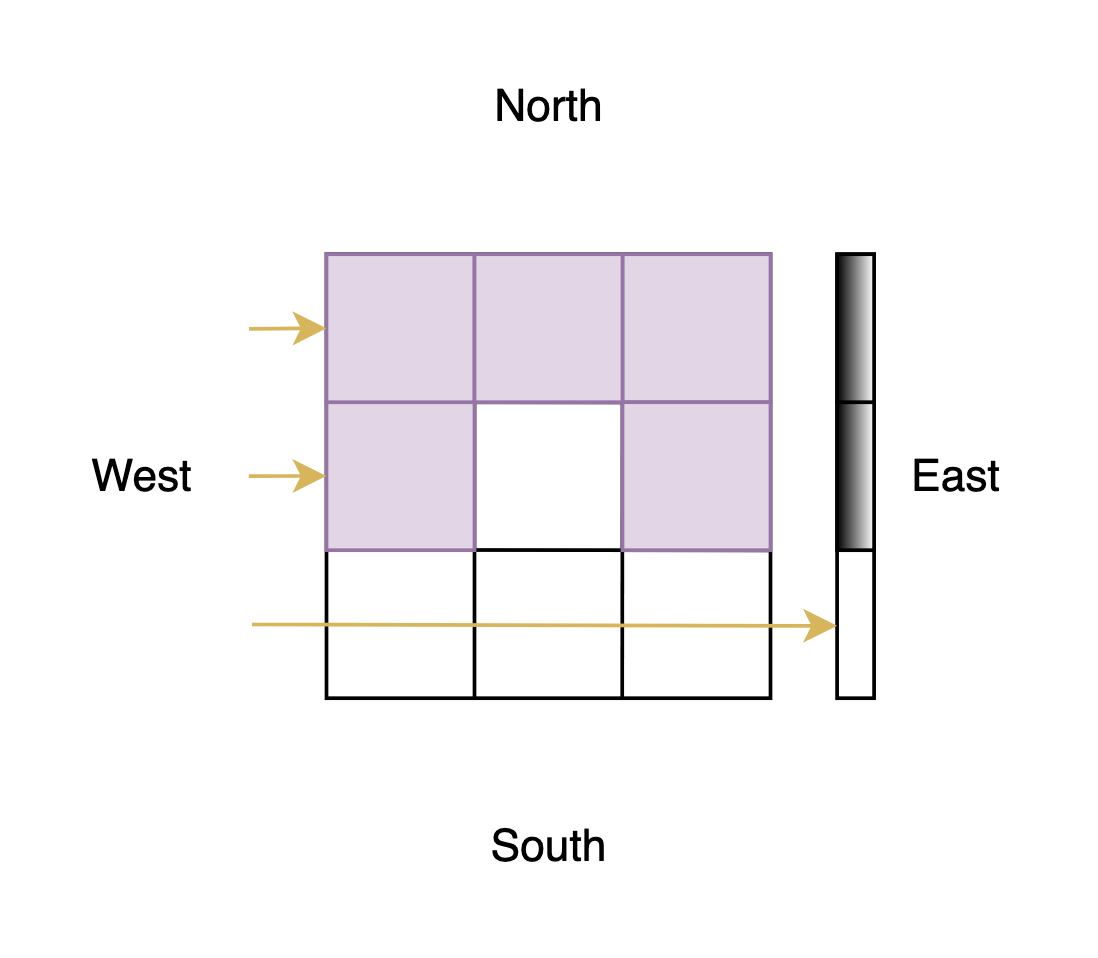
If The knights shoots the beam from the South, the number of shaded positions is ~3~.

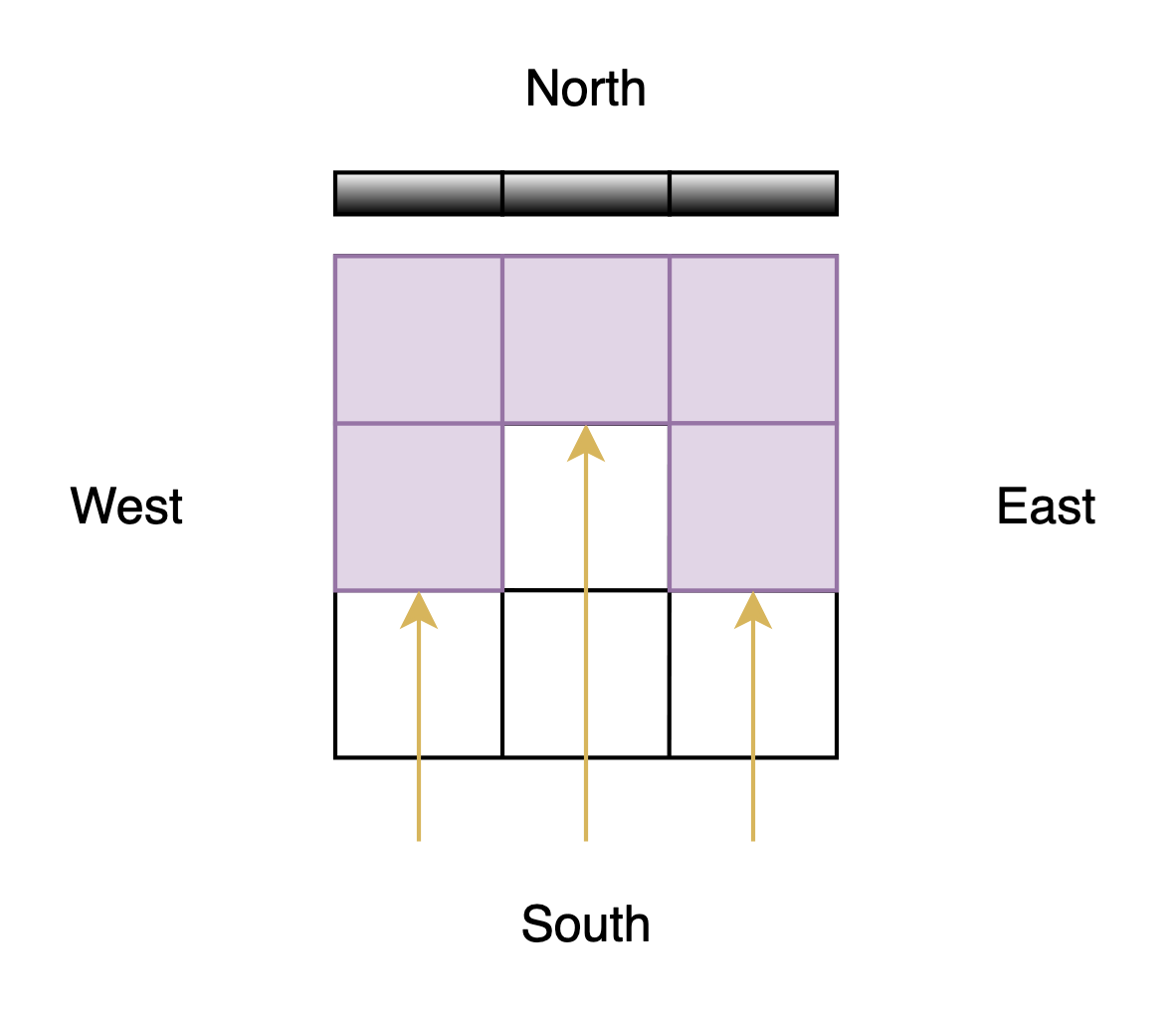
From the east:

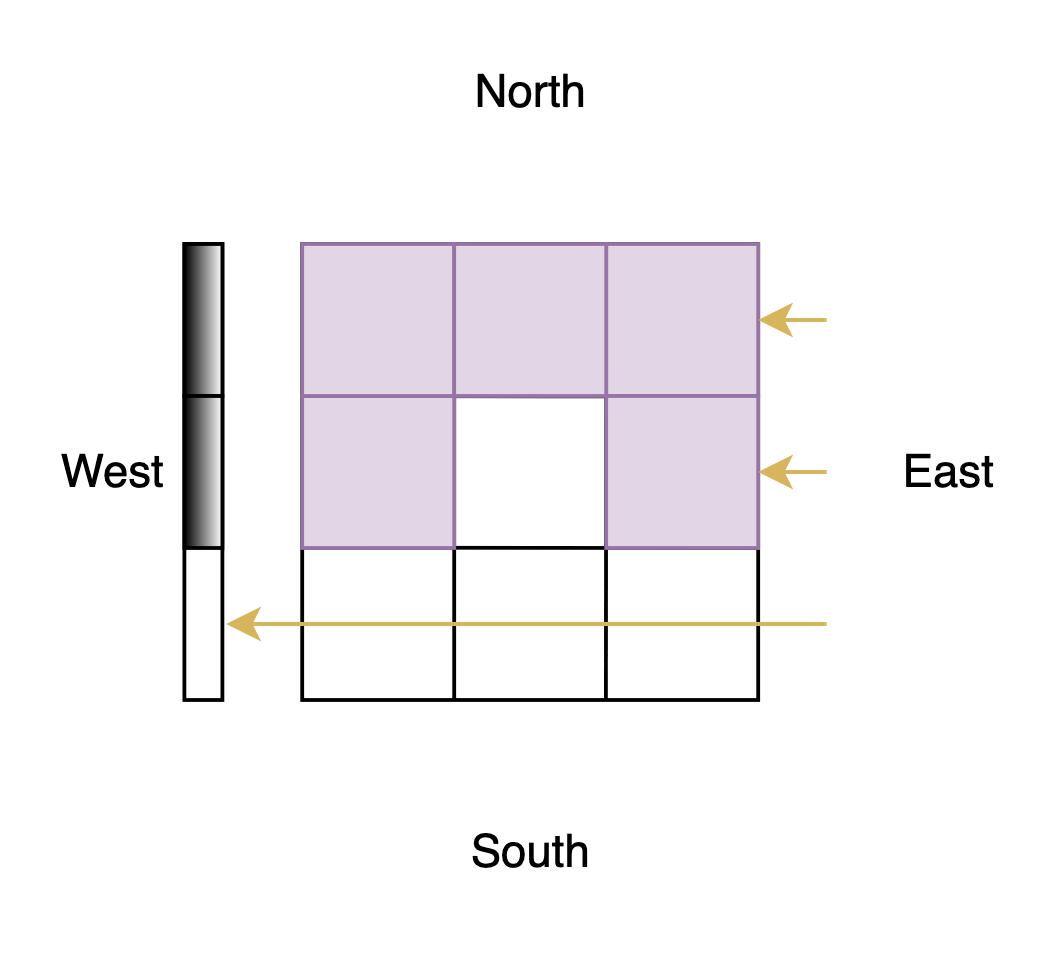
From the north:

In the final showdown at the Las Vegas Casino, two fierce rivals, Kael and Roc, are the last players standing. Currently, Kael has ~x~ chips and Roc has ~y~ chips.

The two will compete in a series of rounds until one player runs out of chips and is eliminated. Let ~z = \min(x, y)~. The outcome of each round follows these rules:

• Kael wins: He takes ~z~ chips from Roc. Kael now has ~x + z~ chips, while Roc has ~y - z~ chips.

• Roc wins: He takes ~z~ chips from Kael. Kael now has ~x - z~ chips, while Roc has ~y + z~ chips.

• Both player draw: No chips are exchanged, and the stack sizes remain ~x~ and ~y~.

Zara, a professional analyst observing the match, has calculated the probabilities for a single round, that Kael has a winning probability of ~p_k~, while Roc has a winning probability of ~p_r~, and the probability of a tie between them is ~1 - p_k - p_r~.

With this data, given that the match will end with one of them running out of chips, Zara wants to know the overall probability that Kael will be the ultimate winner of the competition.

Input

The first line contains a positive integer ~T~ (~1 \leq T \leq 10^5~) — the number of datasets. Each dataset is described as follows:

The first line contains three non-negative integers ~p_k~, ~p_r~, ~b~ (~0 \leq p_k + p_r \leq b \leq 10^8~) — the winning probability of Kael is ~\frac{p_k}{b}~, and the winning probability of Roc is ~\frac{p_r}{b}~.

The second line contains two positive integers ~x~, ~y~ (~1 \leq x, y \leq 10^6~) — the number of chips of Kael and Roc respectively.

The data guarantees that ~\sum{x_i}~ and ~\sum{y_i}~ do not exceed ~10^6~.

Output

The probability that Kael wins overall, expressed in the form ~P \times Q^{-1}~ ~mod~ ~998244353~, where ~Q^{-1}~ is the modular inverse of the denominator modulo ~998244353~.

Sample Input 1

2
2 2 5
4 4
1 2 4
7 5

Sample Output 1

499122177
744721978

Notes

In the first test case, since both players have the same number of chips and the same winning probabilities, their winning probability is ~\frac{1}{2}~.

Bảo is a diligent lumberjack and he is in charge of managing a large, enchanted grove. This grove is quite special: it contains ~n~ ancient trees, each tree ~i~ has an enchantment level of ~a_i~.

The entire grove is interconnected by ~n - 1~ logging paths such that one can travel from any tree to any other tree. The ~j~-th path connects tree ~u~ to tree ~v~ (~u \neq v~). Initially, the entire grove is considered one single, connected "logging zone". The value of a logging zone is the total enchantment level of all trees in that zone.

Every day of Bảo's work, there will be ~q~ events that happened. The events are of three types:

• ~1~ ~x~ — The Cut. Bảo is instructed to permanently remove the ~x~-th logging path. This action will split a single logging zone into two smaller ones. After cutting, Bảo must report the absolute difference between the value of first new zone and the value of second new zone.

• ~2~ ~u~ ~y~ — The Growth. The enchantment level of tree ~u~ suddenly changes by ~y~ (its new value becomes ~a_u = a_u + y~).

• ~3~ — The Boss's Report. Bảo must immediately report to his Boss the value of the most valuable logging zone.

Bảo is sick, can you help him manage the grove for today.

Input

The first line contains a positive integer ~T~ (~T \le 1000~) — the number of test cases.

The first line of each test case contains a positive integer ~n~ (~1 \le n \le 2 \cdot 10^5~) — the number of trees in the grove.

The second line of each test case contains ~n~ integers ~a_1, a_2, \ldots, a_n~ (~|a_i| \le 10^9~) — the enchantment level of each trees.

The next ~n - 1~ lines of each test case contain two integers ~u~ and ~v~ (~1 \le u, v \le n~) — indicating that there is a logging path connecting tree ~u~ and tree ~v~.

The ~n + 2~-th line of each test case contains a positive integer ~q~ (~1 \le q \le 2 \cdot 10^5~) — the number of events.

The next ~q~ lines of each test case are one of the following three types:

• ~1~ ~x~ (~1 \le x \le n - 1~)

• ~2~ ~u~ ~y~ (~1 \le u \le n~, ~|y| \le 10^9~)

• ~3~

For each test case, the total number of type ~1~ queries is guaranteed to appear exactly ~n - 1~ times with distinct values of ~x~.

The total ~n~ is guaranteed not to exceed ~2 \cdot 10^5~ across all tests. The total ~q~ is guaranteed not to exceed ~2 \cdot 10^5~ across all tests.

Output

For each type ~1~ and ~3~ query, output the answer on a new line.

Sample Input 1

1
6
1 1 1 1 1 1
2 6
2 1
4 2
3 4
2 5
5
3
2 2 -6
3
1 2
3

Sample Output 1

6
0
2
1

Notes

In the first example, the following events happened:

• In the first event there is only one logging zone. So the most valuable logging zone has value ~1 + 1 + 1 + 1 + 1 + 1 = 6~.

  

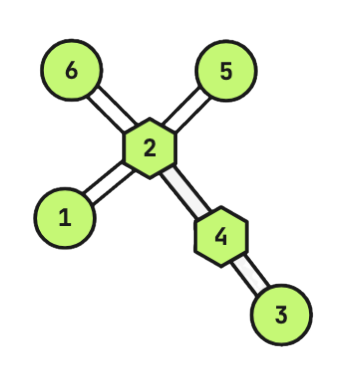
  The initial grove

• In the second event, the second tree's enchantment value got reduced by ~6~.

• In the third event, the most valuable logging zone's value is ~1 + (-5) + 1 + 1 + 1 + 1 + 1 = 0~.

• In the fourth event, the second logging path is removed. There will be ~2~ logging zones. The green colored logging zone (in the second figure) has value ~(-5) + 1 + 1 + 1 + 1 = -1~. The blue colored logging zone has value ~1~. Therefore, the absolute different between two logging zones are ~|1 - (-1)| = 2~.

  

  The grove after the fourth event

• In the fifth event, there are logging zones with values ~1~ and ~-1~. Therefore ~1~ will be report to Bảo's boss.

A disputed territory is defined by ~N~ strategic beacons located at coordinate points on a map. These ~N~ points form a strictly convex polygon.

General Sterling and Colonel Vance have been tasked with establishing a new military base within this territory. Their strategic doctrines, however, are opposed:

• General Sterling advocates for dominance and wants to establish the border to maximize the enclosed area.

• Colonel Vance prioritizes efficiency and defense, aiming to minimize the enclosed area.

To resolve this disagreement, they agree to a strict protocol to define the base's perimeter:

• General Sterling and Colonel Vance take turns negotiating to select a subset of points from the N vertices of the territory to choose as vertices for the base.

• First, General Sterling will go first and select a point as the starting point.

• In each subsequent turn, the negotiating person will choose a point from the remaining points to draw a line connecting to the previously selected point, with the condition that this line must not intersect with any lines that have already been drawn, and the line from this point to the starting point must also not intersect any other lines.

• The negotiation only ends when there are no more points that can be selected, and the two connect the last point to the first point to form a smaller convex polygon and choose it as the military base.

Both individuals are skilled strategists, each knows how to negotiate to optimize their own goals. You are a subordinate of these two and wants to know the result early to plan for the construction of the military base. Calculate the area of the base that these two will draw.

Input

The first line contains a positive integer ~T~ (~1 \leq T \leq 100~) — the number of test cases. The test cases are described as follows:

The first line contains a positive integer ~N~ (~1 \leq N \leq 5000~) — the number of coordinate points on the map.

The second line contains ~N~ positive integers ~x_i~ which are the x-coordinates of the points on the map (~-10^9 \leq x_i \leq 10^9~).

The third line contains ~N~ positive integers ~y_i~ which are the y-coordinates of the points on the map (~-10^9 \leq y_i \leq 10^9~).

The test case guarantees that the points on the coordinates form a convex polygon. The order of the points is arranged in a counterclockwise direction of the convex polygon.

The data guarantees that the total ~\sum{n}~ does not exceed ~5000~.

Output

For each test case, return a single value which is the predicted area that will be drawn. The answer returned should be the area multiplied by ~2~.

It can be proven that the returned answer is an integer.

Sample Input 1

2
4
3 8 5 -2
-7 -5 1 7
5
4 -5 -8 -9 1
-4 5 5 4 -3

Sample Output 1

80
41

Notes

Once vertices 2 and 4 are established, General Sterling selects Point 1 to maximize the resulting area. This choice yields a value of 80, which is bigger to the alternative of 24 (~80 > 24~). Consequently, this is also how the negotiation will play out, as illustrated below.