Bao is a pioneer in Precision Agriculture. His massive plantation is mapped onto an ~n \times n~ coordinate grid, where both rows and columns are numbered from ~1~ to ~n~. Rows are counted from top to bottom, and columns from left to right. To monitor crop health, Bao has installed ~m~ Sentinel Towers at fixed coordinates ~(x_i, y_i)~. No two towers occupy the same grid coordinate.

Bao plans to activate a "Protection Shield" over specific square regions of the field. A Protection Shield covers a square sub-grid of size ~k \times k~ with its top-left corner at (~u,v~).

However, the shield technology requires a perfect energy balance to function. A shield covering a specific sub-grid is considered stable only if it satisfies the Singular Projection Rule:

• Row Stability: Every single row intersecting the sub-grid must contain exactly one Sentinel Tower inside the sub-grid.

• Column Stability: Every single column intersecting the sub-grid must contain exactly one Sentinel Tower inside the sub-grid.

Formally, for a shield of size ~k~ with its top-left corner at (~u,v~), the range of rows is [~u,u+k-1~] and the range of columns is [~v,v+k-1~] the property must hold strictly within these bounds.

Bao has ~q~ queries to process. Each query provides a proposed location (~k,u,v~). Your task is to determine whether a shield activated at this location would be stable.

Input

The first line contains a positive integer ~t~ (~1 \le t \le 1000~) — the number of test cases.

The first line of each test case contains two positive integers ~n~ and ~m~ (~1 \le n \le 2 \cdot 10^5~, ~1 \le m \le \mathrm{min}(2 \times 10^5, n^2)~) — the dimensions of the field and the number of Sentinel Towers.

The next ~m~ lines of each test case contain two positive integers ~x~ and ~y~ (~1 \le x, y \le n~) — the coordinates of the rice plants.

The ~m + 2~-th line of each test case contains a positive integer ~q~ (~1 \le q \le 2 \cdot 10^5~) — the number of queries.

The next ~q~ lines of each test case contain three positive integers ~k~, ~u~, ~v~ (~1 \le k \le n~, ~1 \le u, v \le n - k + 1~) — the square sub-grid with a side length of ~k~ with its top-left point located at cell (~u, v~).

The input data guarantees that the total ~q~ does not exceed ~2 \cdot 10^5~. The input data guarantees that the total ~n~ does not exceed ~2 \cdot 10^5~.

Output

For each query, print Yes on a new line if the shield is stable (satisfies the Singular Projection Rule) otherwise, print No.

Sample Input 1

1
5 7
1 4
2 2
3 3
4 2
4 5
5 1
5 4
5
3 2 2
2 3 2
3 3 1
5 1 1
3 3 3

Sample Output 1

No
Yes
Yes
No
Yes

Notes

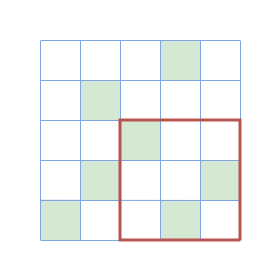
In the first test case, the following figure illustrates the field and the locations of the towers (shown as marked cells):

In the first query, the third column of the subsquare (marked in red) doesn't have a tower.

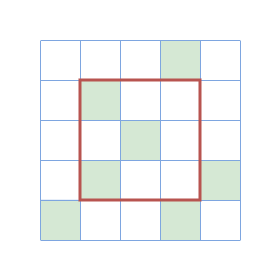
In the second query, the subsquare's shield is stable.

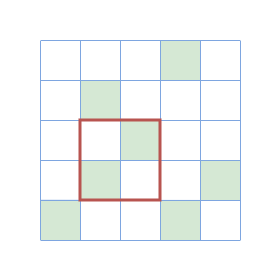
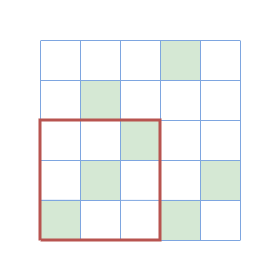
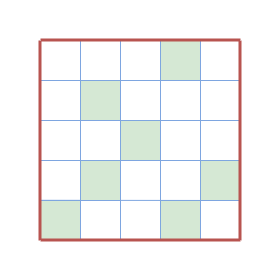
Figures of the 3rd, 4th, and 5th query.